Deciphering dark matter: A computational analysis of stellar velocity distributions

Mingfei Xu

doi:10.54254/2753-8818/13/20240717

1. Introduction

Dark matter (DM), a mysterious substance continues to intrigue the field of astrophysics. Its elusive nature, undetectable through light interaction, leaves us reliant on its gravitational effects on galaxies for indirect observation and understanding. Approximately $$95%$$ of the mass in galaxies and clusters is attributed to an unidentified component, commonly referred to as DM. This assertion is supported by observations from rotation curves (extending to hundreds of kpc), gravitational lensing (up to 200 kpc), and the presence of hot gas in these clusters. (see, e.g., for a review [1]). DM evidences demonstrate that these elusive particles are weakly interacting, non baryonic, stable on cosmological scales and massive. Weakly Interactive Massive particles (WIMPs) are one of the best theoretically motivated models of particle DM [2]. There are different strategies to try to detect DM particle interactions involving cosmic-ray data, collider and direct detection experiments. Despite the huge experimental effort no evidence of DM detection has been proved so far [3-5]. One of the key quantities to study the properties of DM is its density in the Universe and in particular in the Milky Way. Different methods are used to derive the DM density. One of the most powerful is associated with the data of the rotational velocities of stars in the Galaxy. This method, based on the principle that the gravitational effect of DM can influence the speed at which stars move within the Galaxy, has been pivotal in shaping our current understanding of the spatial distribution and abundance of DM (see, e.g., [6]). Due to our position within the Milky Way, achieving precise measurements of the Galaxy's rotation curve has consistently proven to be a considerable challenge [7,8]. The intricate challenges we face in determining the Milky Way's rotation curve have been, in part, a result of the complexities introduced by the dense and obscuring interstellar gas and dust within the Galaxy's disk. Yet, the principal obstacle thus far has been the absence of accurately measured 3D velocities and distances of the stars within the Milky Way. This limitation has been recently surmounted thanks to the second data release (DR2) of the ESA/Gaia mission [9,10]. In a non-MOND (MOdified Newtonian Dynamics) context, the Milky Way's rotation curve (RC) was discerned through observations of various galactic entities. Under the assumption that Newtonian dynamics uniformly governs the interpretation of observational data, the presence of the dark halo (DH) has been corroborated through RC analyses. This article provides a review of current RC observational studies and local DM density profiles within the Newtonian dynamics paradigm [11]. We also provide a new estimate of the possible DH contribution to the dynamic of the Milky Way. In this paper, we introduce an innovative method to fit models to the velocity distributions observed in various Galactic structures, including the DH, bulge, and disk. Particularly concerning the DH, we calculated the associated parameters for different profiles and compared them to the results presented by Cirelli et al. [12]. Our objective is to unearth yet unexplored aspects of DM by investigating the gravitational influences exerted by these various Galactic components. Overall, this study serves as a significant step forward in understanding DM velocity distributions, contributing to the broader landscape of astrophysics.

2. Modeling the Rotation Curve

In this section, we explore three models essential for delineating the Galaxy's rotation curve: the Exponential Disk, The Bulge, and DH. For the Exponential Disk, we utilize modified Bessel functions to model the rotational velocity's decline with radial distance from the GC. In the De Vaucouleurs Bulge model, we employ De Vaucouleurs law, with an exponential decay model to capture the centrally concentrated galactic mass distribution and its impact on the inner rotation curve, Moreover we adopt Exponential Sphere profile to better fit the velocity observed with in 1kpc. For the DH, a critical component despite its invisibility, we adopt both the NFW, gNFW and Isothermal profiles to represent its gravitational influences on the outer sections of the rotation curve. Each model contributes uniquely to our comprehension of the rotation curve, thus enhancing our understanding of the Galaxy's mass distribution and structure.

2.1. Exponential Disk

The Galactic disk is commonly modeled using an exponential disk approach. The RC for such an exponential disk is given by [13]

\begin{equation} V_d(R) = \sqrt{4\pi G\Sigma_0R_dy^2[I_0(y)K_0(y)-I_1(y)K_1(y)]}, \end{equation}

where $$y = R/(2R_d)$$ and $$I_i$$ and $$K_i$$ represent modified Bessel functions[11].

2.2. The Bulge

De Vaucouleurs law, a widely utilized Surface Mass Density (SMD) profile, is typically employed to represent the central bulge. This is based on the assumption that it is proportional to the observed optical profile the surface brightness [14].

\begin{equation} \Sigma_b(R) = \Sigma_{be} \exp[-7.6695((\frac{R}{R_b})^{1/4}-1)], \end{equation}

where $\Sigma_{be}$ corresponds to the value at radius $$ R_b $$ that encompasses half of the total integrated surface mass [15]. It's noteworthy that both the De Vaucouleurs profile and the exponential disk sustain a fixed value at the GC. The volumetric mass density, represented as $\rho(r)$ , at a distinct radius $$ r $$ for a spherically shaped bulge, can be calculated using the Surface Mass Density (SMD). [11].

\begin{equation} \rho(r) = \frac{1}{\pi}\int_r^\infty \frac{d\Sigma_b(x)}{dx}\frac{1}{\sqrt{x^2-r^2}}dx \end{equation}

and the mass within the radius R is:

\begin{equation} M(R) = 4\pi \int^R_0 r^2\rho(r)dr \end{equation}

The circular velocity then, is thus calculated as:

\begin{equation} V_b(R) = \sqrt{\frac{GM(R)}{R}} \end{equation}

In addition to using the De Vaucouleurs bulge model, we have adopted an alternative exponential sphere bulge model to more accurately fit the observed velocities within a 1 kpc radius. In this framework, the volumetric mass density $\rho$ is expressed as an exponential function in terms of radius $$ r $$ using a characteristic scale radius $r_{b}$ [15]:

\begin{equation} \rho(r) =\rho_b \exp(-\frac{r}{R_b}) \end{equation}

In this context, $\rho_b$ represents the bulge density at the GC with the unit of $GeV\cdot cm^{-3}$ . To obtain the mass and then the velocity of the bulge, we adopt the same methodology delineated in Equation (2.4) and (2.5) respectively.

2.3. Dark Matter Halo

A persistent challenge in astrophysics and cosmology has been discerning the distribution of DM surrounding the Milky Way. When examining the distribution of DM in the Milky Way, we investigate various potential scenarios. The NFW profile, which exhibits a peak as $r^{-1}$ at the GC, has been a conventional choice, primarily due to its grounding in N-body simulations [12]. Given that alterations in the DH can influence the estimation of DM density derived from the Milky Way's rotation curve, we employ an alternative parameterization for the DM component. This enables us to account for varying configurations, especially those deviating near the center. Notably, one of the profiles we utilize features a central cusp. We characterize one of our DH profiles as an extended version of the NFW profile, which we denote as gNFW. [16],

\begin{equation} \rho_{{gNFW}}(r) = \rho_s (\frac{r_s}{r})^{\gamma} (1+\frac{r}{r_s})^{\gamma-3}, \end{equation}

where $\rho_0$ is the normalization constant, $$ r_s $$ is the scale radius, and $\gamma$ represents the inner slope. When $\gamma = 1$ , the profile reverts to the widely recognized NFW profile. [17]. The profile is commonly adopted as an approximation for DM densities discerned in cosmological simulations. It depicts a cuspy profile where the density increases significantly towards smaller radial distances.

\begin{equation} \rho_{{NFW}}(r) = \rho_s \frac{r_s}{r} (1+\frac{r}{r_s}). \end{equation}

In addition to the gNFW models, several emerging models have demonstrated competitive performance.Among the various profiles, recent numerical simulations have identified the Einasto profile as offering a superior fit [18,19]. Both the Isothermal [20,21] and Burkert profiles [22] have exhibited good alignment with observational data. Additionally, the Moore model has also produced satisfactory fits based on gNFW model [23]. All considered profiles presuppose spherical symmetry, with $$r$$ being the coordinate centered at the GC [12].

\begin{align} {Einasto}: \rho_{{Ein}}(r) \& = \rho_s \exp\{-\frac{2}{\alpha}[(\frac{r}{r_s})^\alpha-1]\},
{Isothermal}: \rho_{{Iso}}(r) \& = \frac{\rho_s}{1+(r/r_s)^2},
{Burkert}: \rho_{{Bur}}(r) \& = \frac{\rho_s}{(1+r/r_s)(1+(r/r_s)^2)},
{Moore}: \rho_{{Moo}}(r) \& = \rho_s (\frac{r_s}{r})^{1.16} (1+\frac{r}{r_s})^{-1.84}. \end{align}

In order to determine the scale parameters $$r_s$$ and $\rho_s$ , we utilize observational data from the local Milky Way. Specifically, we use the local DM density at the solar radius $r_\odot = 8.33$ kpc [24], which is given as $\rho_\odot = 0.3$ GeV/ $$cm^3$$ . This is a canonical value consistently used in the literature (see, for instance, [25]). The total DM mass contained in 60 kpc is $M_{60} = 4.7\times10^{11} M_\odot$ , This number is based on the kinematic surveys of stars in SDSS [26].

Figure 1. DM profiles, along with the associated parameters to be input into the functional forms delineated in equation 2.9. through 2.12

The normalized density, $\rho_s$ , and the scale radius, $$r_s$$ , are initially unknown for each profile. In order to find them we first use the condition of the local DM density: $\rho(r=r_{\odot})=\rho_{\odot}=0.3$ GeV/cm $$^3$$ . This condition permits to find $\rho_s$ as a function of $$r_s$$ . This implies that the density profile of DM now depends only on $$r_s$$ . In order to find $$r_s$$ we now use the second condition about the total DM mass. To obtain the mass of the DH, we adopt the same methodology delineated in Equation (2.4). This is a non-linear equation that we use using a solver implemented in Python. Upon numerically determining the values of $$r_s$$ and $\rho_s$ , the density profile becomes solely a function of the distance, $$r$$ , from the GC. We show in Fig.~1 the shape of the density profile we find for the different functions and the values of the parameters $\rho_s$ and $$r_s$$ . These values are quite similar with respect to the ones reported in Ref~[12]. In the following we will use the values of the DH density parameters that we find with the previous analysis (see, Fig.~1). We will fix the scale radius while we will leave a re-normalization factor ' $\kappa$ ' which can be explained as a change of the local DH density. Hence, the rotational velocity is redefined as follows:

\begin{equation} V_h(R) = \sqrt{\frac{\kappa GM(R)}{R}}. \end{equation}

3. Fitting the Rotation Curve

In our investigation, we opt for the NFW model ( $\gamma = 1$ ) and the gNFW model for our DH representation. This choice stems from the frequent depiction of rotation velocity as a combined effect of the central black hole (BH), bulge, disk, and the DH:

\begin{equation} V(R) = \sqrt{V_{BH}(R)^2+V_{d}(R)^2+V_{b}(R)^2+V_{h}(R)^2}, \end{equation}

where the notations BH, b, d, and h correspond to black hole, bulge, disk, and DH respectively. When our focus is predominantly on the DH, the influence from the black hole can be largely ignored given its negligible contribution in this context [11]. We employ the least $\chi^2$ fitting method to fit the component of the disk, the Bulge and the DH. It enables us to quantify the discrepancy between our modeled velocity distributions and the observed data, thus validating the efficacy of our methods.

\begin{equation} \chi^2 = \sum_{i=1}^{N} ( \frac{{V(R)_i} - V_{obs,i}}{\sigma_{i}} )^2, \end{equation}

where $$V(R)$$ strand for the model of the rotation curve where the observed velocity $V_{obs}$ and the standard deviation $\sigma_{i}$ are respect to the radius are observational data [11]. Leveraging the model presented in the previous section, and utilizing the $$r_s$$ and $\rho_s$ values discerned from Figure 1, we are able to derive the parameters of each component. We start by assuming for the DH a NFW profile. Table 1 enumerates these parameters, as established from the previous section, assuming slope parameter $\gamma = 1$ . Consequently, we can ascertain the change in modeled velocity purely as a function of radius. The chi-square ( $\chi^2$ ) statistics for the NFW model, with $\gamma = 1$ , yield values of 96.52 and 93.03 for the De Vaucouleurs bulge and the exponential bulge respectively. These values provide a comparative measure of how well each model aligns with the observed data. Additionally, we implemented the Moore model, which can be considered a gNFW model at $\gamma = 1.16$ . The corresponding scale parameters and fitting plots for the two models with different slope parameters are presented in Table 1, Figure 2 and Figure 3, respectively. When evaluating the Moore model with $\gamma = 1.16$ , we obtained chi-square ( $\chi^2$ ) statistics of 96.52 and 75.24 for the De Vaucouleurs bulge and the exponential bulge.

Table 1: Values with error for the scale Parameters of De Vaucouleurs Bulge and Exponential Bulge and the Exponential disk, the slope parameters are $\gamma = 1$ and $\gamma = 1.16$ respectively.

	$\gamma = 1$		$\gamma = 1.16$
Parameter	De Vaucouleurs	Exponential	De Vaucouleurs	Exponential
$$R_d$$ [kpc]	$12.4\pm0.8$	$7.7\pm0.3$	$12.7\pm0.8$	$7.8\pm0.3$
$\Sigma_d$	$8.8^{+0.4}_{-0.4}\times 10^{17}$	$10.1^{+0.4}_{-0.3}\times10^{17}$	$5.5^{+0.3}_{-0.3}\times 10^{17}$	$8.8^{+0.4}_{-0.4}\times10^{17}$
$$R_b$$ [kpc]	$0.739\pm0.044$	$0.139\pm0.003$	$0.673\pm0.042$	$0.136\pm0.003$
$\Sigma_{\lt strong\gt be\lt /strong\gt }$	$-1.3^{+0.1}_{-0.1}\times 10^{38}$	-	$-1.4_{-0.1}^{+0.1}\times 10^{38}$	-
$\rho_b[Gev/cm^3]$	-	$5.7^{+0.3}_{-0.3}\times10^{-4}$	-	$3.0^{+0.3}_{-0.3}\times10^{-4}$
$\kappa$	$1.01^{+0.05}_{-0.05}$	$1.17^{+0.04}_{-0.04}$	$0.90^{+0.04}_{-0.04}$	$1.04^{+0.04}_{-0.03}$

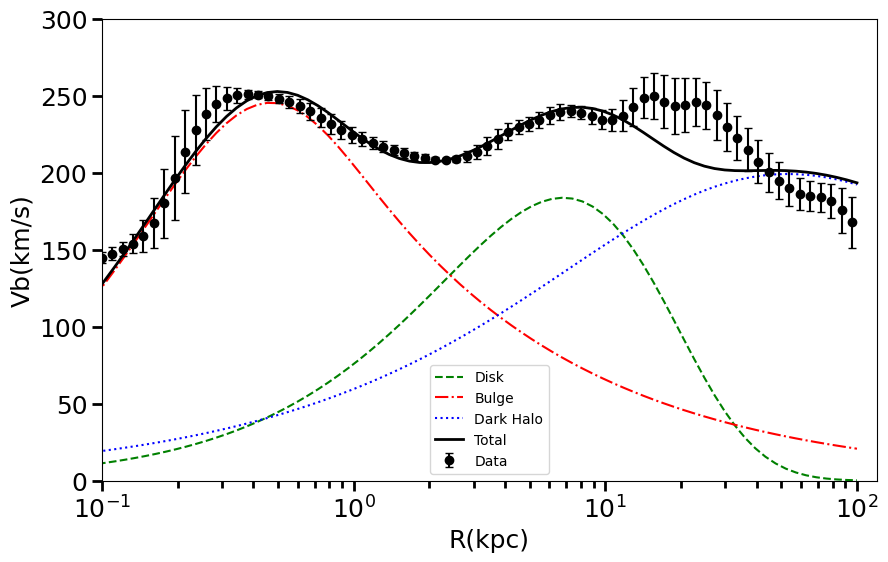
Figure 2. NFW( $\gamma=1$ )-Exponential Sphere Bulge log-scale

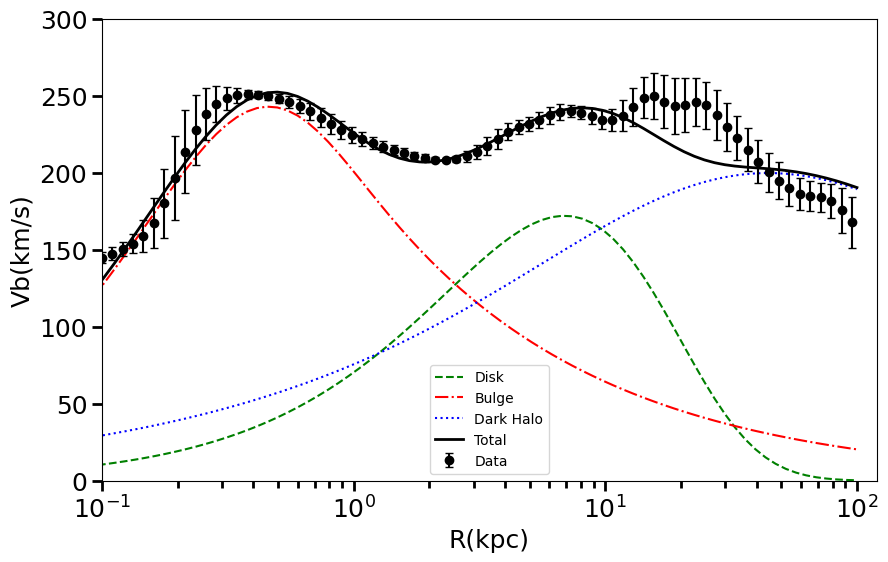
Figure 3. gNFW( $\gamma=1.16$ )-Exponential Sphere Bulge log-scale

As illustrated in Figure 2, the De Vaucouleurs Bulge model provides a more accurate fit for data points at larger radii (r $\gt$ 50kpc), implying a better representation of the DH. However, this model overestimates the velocity within a radius of 1kpc. On the other hand, the Exponential Bulge model successfully captures the rotation curve closer to the GC, but it seems to require a larger slope parameter of the gNFW profile to optimally fit the rotation curve at larger radii. Overall, the rotation curve associated with the exponential bulge profile is more sensitive to the variation of the slope parameter, $\gamma$ . Allowing $\gamma$ to freely vary results in an optimal fit for the exponential bulge that yields a surprisingly low $\chi^2$ value of 30.52, corresponding to $\gamma=1.61$ . This result, however, is not acceptable due to the exceedingly large value of $\gamma$ . In fact, numerical simulations point towards values of $\gamma$ between 1.0-1.4. Moreover, we have also incorporated the Isothermal model in our analysis as a point of comparison to the gNFW profile. As a result of this comparison, we obtained chi-square values of 131.13 and 101.05 for the exponential bulge and De Vaucouleurs bulge, respectively. The scale parameters and fitting plots are shown in Table(2) and Figure (4).

Table 2: Values with error for the scale Parameters of De Vaucouleurs Bulge and Exponential Bulge of the Isothermal DH model

Parameter	De Vaucouleurs	Exponential Sphere
$$R_d$$ [kpc]	$12.3\pm0.8$	$7.1\pm0.3$
$\Sigma_0$	$6.4^{+0.3}_{-0.3}\times10^{17}$	$10.2^{+0.4}_{-0.4}\times10^{17}$
$$R_b$$ [kpc]	$0.889\pm0.051$	$0.143\pm0.003$
$\Sigma_{\lt strong\gt be\lt /strong\gt }$	$1.06^{+0.07}\times10^{38}$	-
$\rho_b[Gev/cm^3]$	-	$5.46^{+0.02}_{-0.02}\times10^{-4}$
$\kappa$	$1.00^{+0.05}_{-0.05}$	$1.18^{+0.04}_{-0.04}$

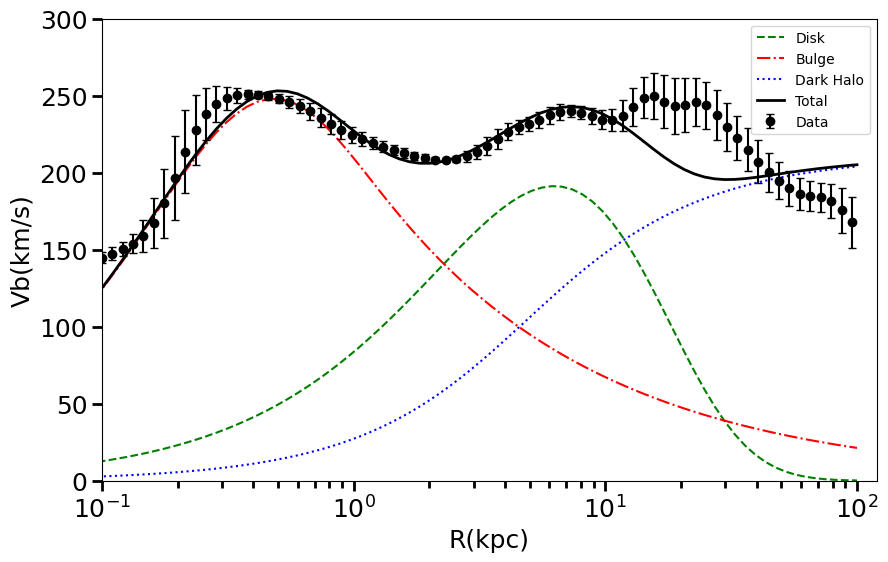
Figure 4. Isothermal-Exponential Sphere Bulge log-scale

The fit achieved with the Isothermal profile doesn't align as well as the one obtained using the gNFW profile. Generally, the $\chi^2$ value for the Isothermal model is larger compared to that of the gNFW model, indicating a poorer fit. Furthermore, the Isothermal profile exhibits an increasing trend at larger radii, which contradicts the decreasing trend observable in the data.

4. Conclusions

In this paper we have investigated the density of dark matter in the Milky Way by fitting the latest data for the rotational velocities of stars. In order to do this we consider three components: the disk the bulge and the DH. For the disk we parameterize the density with a modified Bessel which is related to the exponential disk model. The disk component has two parameters: $\Sigma_d$ which governs normalization and $$R_d$$ which moves the peak velocity at certain radius from the GC. For the bulge component we adopted a De Vaucouleurs function which is related to the SMD profile that is assumed to be proportional to the empirical optical profile of the surface brightness. This model allows us to better fit the velocity for large radii. Meanwhile, we also employed the Exponential Sphere bulge model to better fit observed velocity close to the GC. Finally, For the DH model, we employed the generalized gNFW profile with two different slope parameters: $\gamma=1$ (corresponding to the standard NFW model) and $\gamma =1.16$ (corresponding to the Moore model). Simultaneously, we adopted the contrasting Isothermal profile for comparison. We established our models using the measured local Dark Matter density at the solar radius and the total Dark Matter mass contained within a 60 kpc radius as a boundary condition to determine the parameters $$r_s$$ and $\rho_s$ for the respective profiles. We employed the classic Newtonian approach to ascertain the circular velocity. Meanwhile, we use the least chi-squire ( $\chi^2$ ) method to fit the rotation curve. Our analysis demonstrate that the disk, bulge and DH components can fit very well the rotational velocity data from radii of 0.1 to 100 kpc from the GC. In particular, the bulge contributes in the inner part of the Galaxy up to radii of a few kpc. The disk dominates the dynamic from a few kpc up to a 20 kpc. At large distances from the GC the DH drives the star velocities. This is a result which is independent from the density profile used. In particular, at distances from the GC above 50 kpc the DH makes at most the $$80%$$ of the rotational velocity.

References

[1]. K. Freese. Review of Observational Evidence for Dark Matter in the Universe and in upcoming searches for Dark Stars. In E. Pecontal, T. Buchert, Ph. di Stefano, and Y. Copin, editors, ´ EAS Publications Series, volume 36 of EAS Publications Series, pages 113–126, January 2009. doi: 10.1051/eas/0936016.

[2]. Jonathan L. Feng. Dark Matter Candidates from Particle Physics and Methods of Detection. Annual Review of Astronomy and Astrophysics, 48:495–545, September 2010. doi: 10.1146/annurev-astro 082708-101659.

[3]. Jennifer M. Gaskins. A review of indirect searches for particle dark matter. Contemporary Physics, 57(4):496–525, October 2016. doi: 10.1080/00107514.2016.1175160.

[4]. Antonio Boveia and Caterina Doglioni. Dark Matter Searches at Colliders. Annual Review of Nuclear and Particle Science, 68:429–459, October 2018. doi: 10.1146/annurev-nucl-101917- 021008.

[5]. Teresa Marrodan Undagoitia and Ludwig Rauch. Dark matter direct-detection experiments. ´ Journal of Physics G Nuclear Physics, 43(1):013001, January 2016. doi: 10.1088/0954-3899/43/1/013001.

[6]. Yoshiaki Sofue and Vera Rubin. Rotation Curves of Spiral Galaxies. Annual Review of Astronomy and Astrophysics, 39:137–174, January 2001. doi: 10.1146/annurev.astro.39.1.137.

[7]. Yoshiaki Sofue. Grand Rotation Curve and Dark Matter Halo in the Milky Way Galaxy. Publications of the Astronomical Society of Japan, 64:75, August 2012. doi: 10.1093/pasj/64.4.75.

[8]. D. Russeil, A. Zavagno, P. Mege, Y. Poulin, S. Molinari, and L. Cambresy. The Milky Way ` rotation curve revisited. Astronomy and Astrophysics, 601:L5, May 2017. doi: 10.1051/0004- 6361/201730540.

[9]. Gaia Collaboration, A. G. A. Brown, and Vallenari et al. Gaia Data Release 2. Summary of the contents and survey properties. Astronomy and Astrophysics, 616:A1, August 2018. doi: 10.1051/0004-6361/201833051.

[10]. Gaia Collaboration, A. Helmi, and F. van Leeuwen et al. Gaia Data Release 2. Kinematics of globular clusters and dwarf galaxies around the Milky Way. Astronomy and Astrophysics, 616: A12, August 2018. doi: 10.1051/0004-6361/201832698.

[11]. Yoshiaki Sofue. Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies, 8(2):37, April 2020. doi: 10.3390/galaxies8020037.

[12]. Marco Cirelli, Gennaro Corcella, Andi Hektor, Gert Hutsi, Mario Kadastik, Paolo Panci, Martti ¨ Raidal, Filippo Sala, and Alessandro Strumia. PPPC 4 DM ID: a poor particle physicist cookbook for dark matter indirect detection. Journal of Cosmology and Astroparticle Physics, 2011(3):051, March 2011. doi: 10.1088/1475-7516/2011/03/051.

[13]. James Binney and Scott Tremaine. Galactic dynamics, volume 20. Princeton university press, 2011.

[14]. G. de Vaucouleurs. Photoelectric photometry of the Andromeda Nebula in the UBV system. Astrophysical Journal, 128:465, November 1958. doi: 10.1086/146564.

[15]. Yoshiaki Sofue. Rotation and mass in the Milky Way and spiral galaxies. Publications of the Astronomical Society of Japan, 69(1):R1, February 2017. doi: 10.1093/pasj/psw103.

[16]. P. F. de Salas, K. Malhan, K. Freese, K. Hattori, and M. Valluri. On the estimation of the local dark matter density using the rotation curve of the Milky Way. Journal of Cosmology and Astroparticle Physics, 2019(10):037, October 2019. doi: 10.1088/1475-7516/2019/10/037.

[17]. Julio F. Navarro, Carlos S. Frenk, and Simon D. M. White. A Universal Density Profile from Hierarchical Clustering. Astrophysical Journal, 490(2):493–508, December 1997. doi: 10.1086/304888.

[18]. David Merritt, Alister W. Graham, Ben Moore, Jurg Diemand, and Bal ¨ sa Terzi ˇ c. Empirical ´ Models for Dark Matter Halos. I. Nonparametric Construction of Density Profiles and Comparison with Parametric Models. The Astronomical Journal, 132(6):2685–2700, December 2006. doi: 10.1086/508988.

[19]. Julio F. Navarro, Aaron Ludlow, Volker Springel, Jie Wang, Mark Vogelsberger, Simon D. M. White, Adrian Jenkins, Carlos S. Frenk, and Amina Helmi. The diversity and similarity of simulated cold dark matter haloes. Monthly Notices of the Royal Astronomical Society, 402(1): 21–34, February 2010. doi: 10.1111/j.1365-2966.2009.15878.x.

[20]. K. G. Begeman, A. H. Broeils, and R. H. Sanders. Extended rotation curves of spiral galaxies : dark haloes and modified dynamics. Monthly Notices of the Royal Astronomical Society, 249:523, April 1991. doi: 10.1093/mnras/249.3.523.

[21]. J. N. Bahcall and R. M. Soneira. The universe at faint magnitudes. I. Models for the Galaxy and the predicted star counts. The Astrophysical Journal, 44:73–110, September 1980. doi: 10.1086/190685.

[22]. A. Burkert. The Structure of Dark Matter Halos in Dwarf Galaxies. The Astrophysical Journal, 447:L25–L28, July 1995. doi: 10.1086/309560.

[23]. Jurg Diemand, Ben Moore, and Joachim Stadel. Convergence and scatter of cluster density ¨ profiles. Monthly Notices of the Royal Astronomical Society, 353(2):624–632, September 2004. doi: 10.1111/j.1365-2966.2004.08094.x.

[24]. S. Gillessen, F. Eisenhauer, S. Trippe, T. Alexander, R. Genzel, F. Martins, and T. Ott. Monitoring Stellar Orbits Around the Massive Black Hole in the Galactic Center. Astrophysical Journal, 692 (2):1075–1109, February 2009. doi: 10.1088/0004-637X/692/2/1075.

[25]. G. Jungman, M. Kamionkowski, and K. Griest. Supersymmetric dark matter. Physics Reports, 267:195–373, March 1996. doi: 10.1016/0370-1573(95)00058-5.

[26]. X. X. Xue, H. W. Rix, G. Zhao, P. Re Fiorentin, T. Naab, M. Steinmetz, F. C. van den Bosch, T. C. Beers, Y. S. Lee, E. F. Bell, C. Rockosi, B. Yanny, H. Newberg, R. Wilhelm, X. Kang, M. C. Smith, and D. P. Schneider. The Milky Way’s Circular Velocity Curve to 60 kpc and an Estimate of the Dark Matter Halo Mass from the Kinematics of ˜2400 SDSS Blue Horizontal-Branch Stars. Astrophysical Journal, 684(2):1143–1158, September 2008. doi: 10.1086/589500.

Cite this article

Xu,M. (2023). Deciphering dark matter: A computational analysis of stellar velocity distributions. Theoretical and Natural Science,13,1-10.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of the 3rd International Conference on Computing Innovation and Applied Physics

ISBN：978-1-83558-189-6(Print) / 978-1-83558-190-2(Online)

Editor：Yazeed Ghadi

Conference website: https://www.confciap.org/

Conference date: 27 January 2024

Series: Theoretical and Natural Science

Volume number: Vol.13

ISSN：2753-8818(Print) / 2753-8826(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).