1. Introduction

In the contemporary dynamic and competitive landscape, understanding and meeting the preferences of clients is crucial for sustained success. However, applying an excessive number of resources to explore these preferences can lead to deficits and inefficiencies. Therefore, efficient resource allocation strategy is crucial. Businesses often allocate more funding for a marketing input with higher effectiveness (for example, higher sales) than one with lower effectiveness [1]. Due to the restricted marketing budget, marketers need to figure out how to get the most of their spending. [2] With a reasonable cost of promotional resources, high-efficiency marketing can quickly attract a big number of potential clients. Hence, it is necessary for businesses to achieve a balance of recourse spending on between conducting market research to gather user's feedback on certain product or service and deploying innovative strategies to meet customer demands [2]. Relying on data-driven insights and advanced analytics can facilitate companies to focus their efforts on the most promising areas, avoiding wasteful spending and optimizing resource utilization.

In this case, businesses are constantly looking for innovative ways to optimize their promotion and recommendation strategies. For instance, the Multi-armed Bandit algorithm, which offers a powerful framework for tackling the exploration-exploitation trade-off problem [3], is a remarkable tool in this field. Inspired by the concept of casino slot machines with multiple arms, the algorithm enables companies to intelligently allocate resources among various options to maximize rewards and minimize risks. In promotion strategies, the Multi-armed Bandit algorithm empowers marketers to efficiently allocate resources across a variety of channels, constantly adapting to instant feedbacks to maximize revenue conversion. Similarly, it can optimize the personalized suggestions and advertisements through the interactive learning of users in the recommender system to improve user satisfaction and maximize benefits. Therefore, by utilizing adaptive and data-driven nature of the Multi-armed Bandit algorithm, businesses can benefit from efficiency by an optimized Multi-armed Bandit algorithm. It is noteworthy that there are multiple types of Multi-armed Bandit algorithms, including Explore-Then-Commit (ETC) [4], Upper Confidence Bound (UCB) [5], and Thompson sampling [4]. These three algorithms apply through different methods to select the best arm based on the data explored. The ETC algorithm explores the arms by playing each arm a predetermined number of times before exploiting by committing to the arm that showed the most promise during exploration [4]. In comparison, UCB algorithms employ an optimistic approach, estimating the upper confidence bound for each arm's expected reward based on the number of times it has been pulled. It involves the UCB indices, which offer upper confidence limits on the rewards connected to the channels the secondary user may be able to exploit [5], and then selects the arm with the highest estimated upper bound. In addition, the Thompson Sampling algorithm employs a Bayesian approach to model the underlying distribution of each arm's reward. It adopts a posteriori sampling to determine the best optimal arm for exploitation [4]. The performance of these algorithms regarding regret, which measures the cumulative difference between the rewards earned and those that would have been obtained by always selecting the best arm, can vary in different scenarios. The motivation for researching regret differences in real-world applications arises from the need to make informed decisions in dynamic environments. As variables change over time and the number of experiments grows, the performance of MAB algorithms can fluctuate. Understanding which algorithm suits a particular scenario can optimize resource allocation and improve overall outcomes. Hence, it is important to research on different algorithms' performance under different scenarios to analyze the algorithm to utilize in suitable situations. Yağan optimized the Multi-armed Bandit algorithm by developing C-Bandit algorithms, effectively reducing the common K-arm bandit algorithm to a C-arm bandit algorithm [6]. Their research introduced the Correlated UCB algorithm (C-UCB), which required only \( O(1) \) time to select sub-optimal arms, while K-arm UCB algorithms required \( O(logT) \) time [6]. The utilization of loose pseudo-rewards in C-Bandit algorithms enabled them to perform at least as well as K-Bandit algorithms [6].

With the above regards, an experiment testing performance of different algorithms on a real dataset under different scenarios is required. Using the movie lens dataset as the object of analysis, this study considered the movie categories as arms. Each experimental individual for each movie were categorized into this movie category, and the study analyzed the frequency of ratings of movie categories to calculate the reward, considered as rating of a category, for selecting some genre. Depending on the different variables and parameters to control the environment the dataset is used to test the algorithms, the experimenter runs different algorithmic implementation programs to analyze the dataset and output the regrets obtained from each experiment. Through the simulation of each scenario, the research will produce a valid conclusion on performance of each algorithm to support the readers to make accurate selections of algorithms in real-world application.

2. Methods

2.1. Dataset description and preprocessing

The study aimed to investigate varying regret outcomes by conducting multiple iterations of the Multi-armed Bandit algorithm on the MovieLens dataset, employing diverse parameter settings. The MovieLens dataset is a widely used and comprehensive movie recommendation dataset compiled by the GroupLens Research team at University of Minnesota. The dataset was originally released for research purposes to facilitate the development and evaluation of collaborative filtering algorithms for movie recommendations [6]. The MovieLens 1M dataset contains ratings and other user information collected from MovieLens [7], an online movie recommendation service. The data includes movie ratings given by users, demographic information. Specifically, the dataset comprises one million movie ratings given by 6,000 users on 4,000 movies. Each movie is rated on a scale of 1 to 5, with 1 being the lowest rating and 5 being the highest.

To observe the performance of the three Multi-armed Bandit algorithm, this study selected the movies' genres as arms, and the user's rating on a genre as the reward received when the user selected the particular genre. In detail, the comparison of performance of the algorithms would be differences in terms of expected cumulative regret produced in round \( t \) , when \( t = 1, 2,...,n \) . The value of \( n \) here represented the horizon, signifying the total number of rounds the algorithm was used. As mentioned earlier, the MovieLens dataset contains abundant information that is unnecessary for testing the algorithms, such as demographic details about the users. To address this, the experiments conducted data analysis, to preprocess the raw data and extract only the relevant portion required for algorithm testing. Specifically, the dataset comprises three files containing information on ratings, user profiles, and movie details. While each file contains the necessary data for analysis, it also includes extraneous information. Consequently, the dataset files were opened and loaded separately using a comma-separated values format. The preprocessing program then merged the files while appropriately separating the genres of movies, as a single movie could be classified under multiple genres. Following this, the program accessed the unique genres of each movie and mapped them into corresponding indices. Calculating the ratings and probabilities required for the subsequent steps, the frequency of ratings for each genre was computed from the preprocessed file. Finally, the preprocessing program developed a pull-arm function to determine the reward of selecting a genre based on the values of ratings and probabilities.

2.2. ETC

The fundamental idea behind the ETC algorithm involves dividing the exploration and exploitation phases into distinct segments. During the initial exploration phase, the algorithm randomly selects arms to gather information about their rewards. After a predetermined number of rounds, which was defined as value \( m \) in this study, the algorithm transitions to the exploitation phase, where it commits to the arm that appeared most promising during the exploration phase. The basic principle of explore-then-commit is to strike a balance between exploring different arms and exploiting the most promising one after sufficient exploration. In the implementation, the cumulative regret was calculated separately for the two phases by summing up the differences between the reward and the optimal reward.

2.3. UCB

The UCB algorithm aims to balance exploration and exploitation effectively. It achieves this by calculating upper confidence bounds for each arm's expected reward based on observed rewards and confidence intervals. In each round, the algorithm selects the arm with the highest upper confidence bound, leading to a balance between choosing arms that appear promising based on existing data and exploring new arms to gather more information. As it runs over time, the algorithm will achieve near-optimal cumulative rewards. In the implementation, the cumulative regret was calculated on the arm with the maximum number of UCB indices which sums up by empirical mean of rewards and the exploration bonus (confidence width).

2.4. Thompson sampling

The idea behind Thompson Sampling is to model uncertainty about the rewards of each arm using Bayesian probability distributions. The basic principle involves sampling from these distributions to make decisions. During each round, arms are randomly selected according to their respective probabilities of being the best arm, based on the sampled values. This randomization effectively balances exploration and exploitation. As the algorithm observes more data, the belief distributions get updated, allowing Thompson Sampling to adapt and converge to the best-performing arm over time. In the implementation, the cumulative regret was calculated on the arm selected from the sample.

2.5. Implementation details

In general, the study started by fixing the number of experiments as 100 and choosing the horizon as 50,000 rounds. By running the program and plotting the cumulative regret graph for each algorithm, observations of the algorithms' performance could be intuitively visualized. Also, the study conducted an environment where it chose the number of experiments as 10 and remained the rest variables to observe the variance of the algorithms clearly.

To select the algorithm suitable in some specific real-world situations, this study not only changed the number of rounds but also changed the parameter individually for ETC and UCB algorithm to determine the conditions they perform best. First, the study adjusted the value of horizon, setting five different levels from 500 to 5,000,000, and tested the three algorithms to check whether they changed performance over number of rounds.

The study then modified the parameters of ETC algorithm. Since ETC's exploration and exploitation are separated explicitly, the study wanted to learn ETC's performance from different length of exploration phase. Hence, it changed the controlled value \( m \) , which symbolized the length of exploration, to realize the objective.

In addition, the study modified the experiment on UCB algorithm. It started with the regular UCB algorithm, shifting the time that sub-optimal arm was selected by controlling the constant value l. Then, it compared the performance of regular UCB algorithm with the asymptotically optimized UCB algorithm. To compare, while the common UCB algorithm uses a logarithmic exploration rate, the asymptotically optimized version employs a polynomial exploration rate. This modification leads to improved performance in certain scenarios, as the polynomial exploration rate helps the algorithm better adapt to changing reward distributions and reduces the risk of over-exploration. Hence, by comparison of asymptotic optimized UCB algorithm with regular UCB, the study could determine the best usage of UCB algorithm with different times of sub-optimal arm selection. Lastly, the study would compare once more among the three algorithms with asymptotically optimized UCB with horizon being 1,000,000.

3. Results and discussion

3.1. The performance of various algorithms

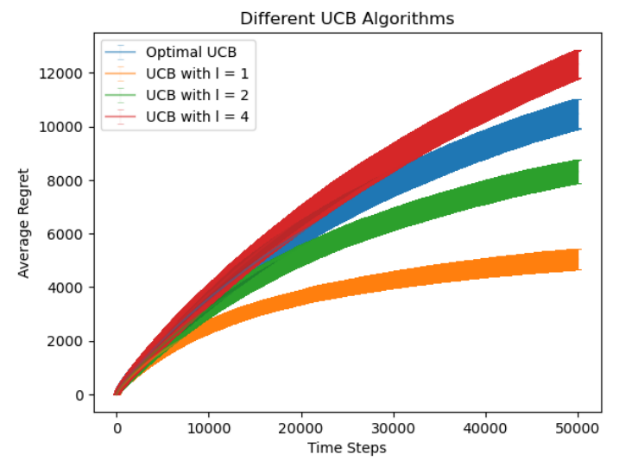
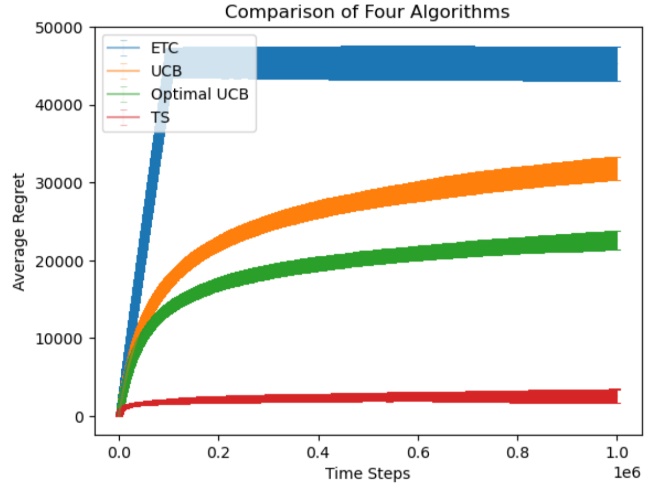
The study conducted a series of experiments investigating various algorithms, yielding several sets of graphs to analyze the results. In Figure 1, the lines exhibited the cumulative regret when choosing number of experiments as 100 and horizons as 500, 5,000, 50,000, 500,000, and 5,000,000. As mentioned, Figure 2 explored the variance of the algorithms when running few experiments. Figure 3 displayed the performance of ETC algorithm under different \( m \) values. In addition, Figure 4 presented experimental outcomes for the regular UCB algorithm across varying 'l' values and compared them with the asymptotically optimal UCB algorithm. Ultimately, Figure 5 demonstrated the experiment on the original three algorithms with the asymptotically optimal UCB algorithm in the condition of horizon being 1,000,000.

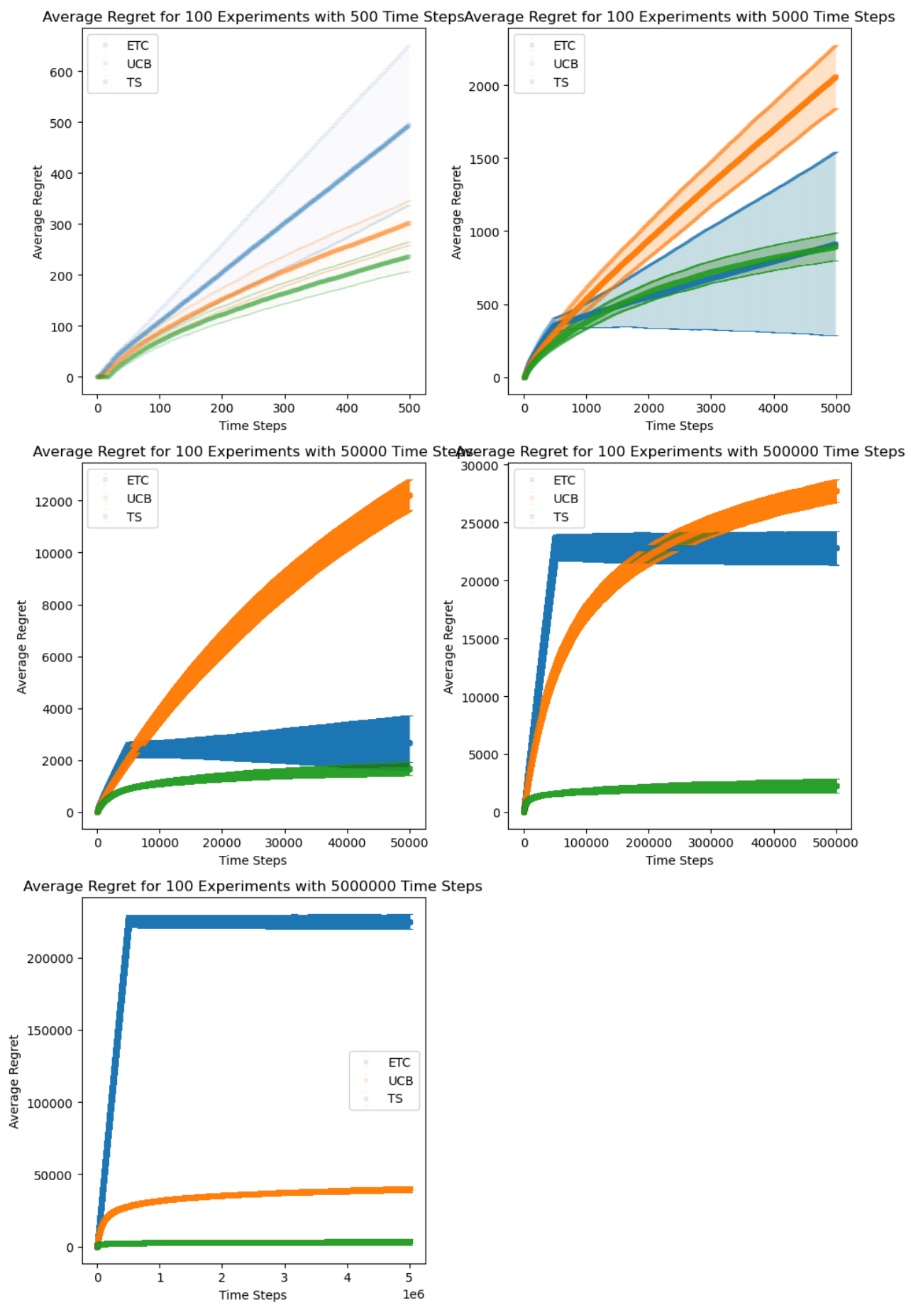
Figure 1. Average Regret of ETC, UCB, TS for 100 Experiments with different Time Steps.

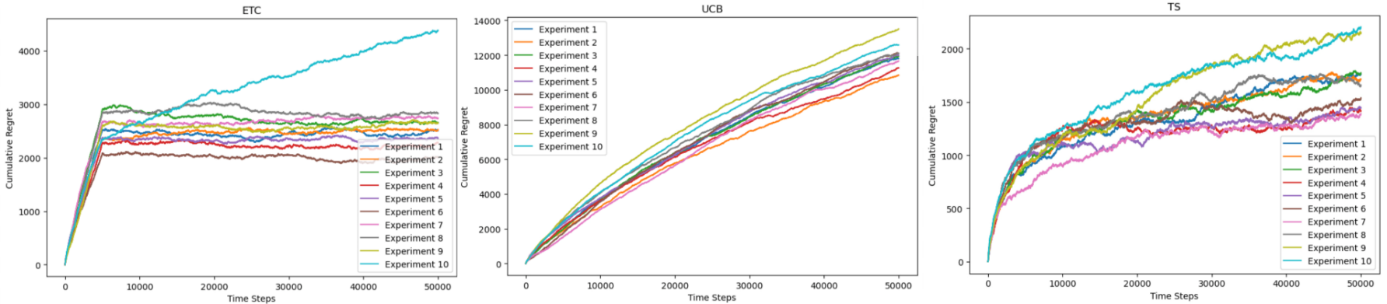
Figure 2. Cumulative Regret of ETC, UCB, TS for 10 Experiments with 50,000 Time Steps.

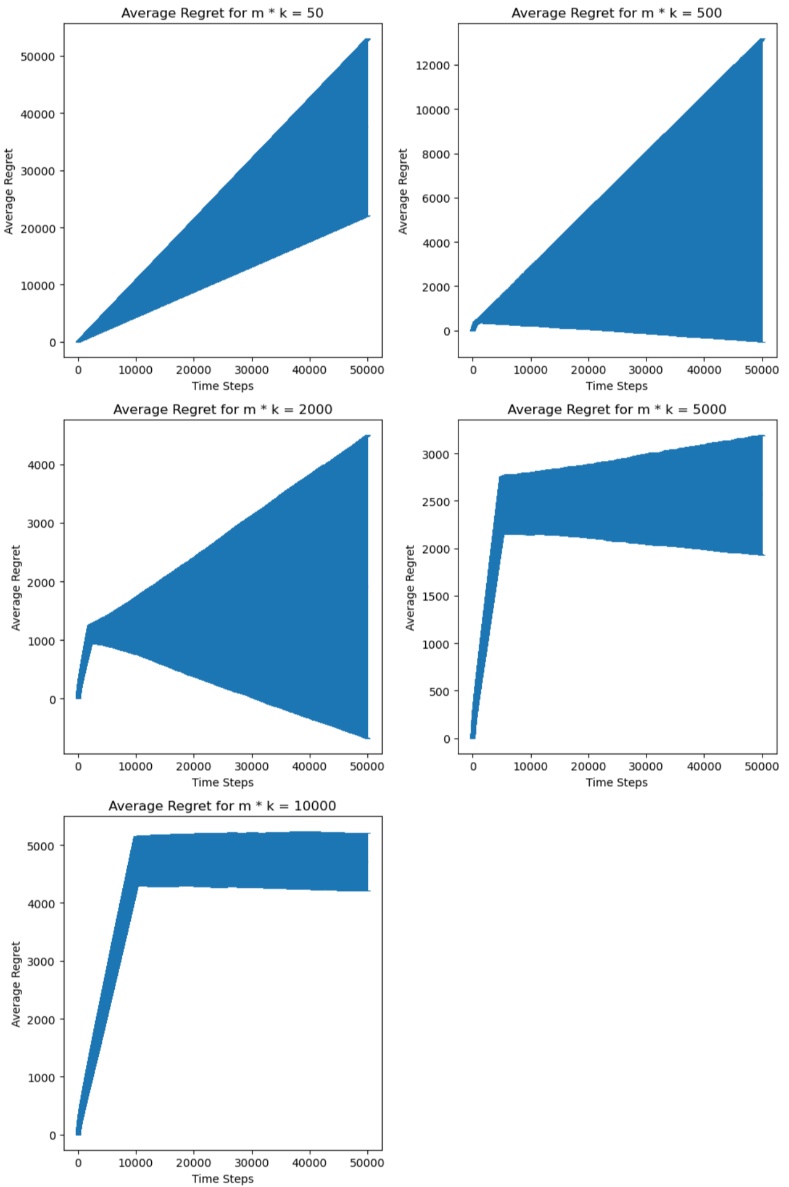
Figure 3. Average Regret of ETC for 100 Experiments with different \( m * k \) .

3.2. Discussion

The figures in the study display cumulative regrets of various algorithms, distinguished by four different colors of curves and lines. In Figure 1, the orange line represents the ETC algorithm, the blue curve symbolizes the standard UCB algorithm, and the green curve demonstrates the Thompson Sampling algorithm. The Figure 3 only presents the ETC algorithm. The blue curve in Figure 4 represents the regret of asymptotically optimal UCB algorithm, with the red, green, and orange curves representing standard UCB algorithm with \( l \) value being 4, 2, and 1. Lastly, in Figure 5, the orange line represents the ETC algorithm, the red curve symbolizes the standard UCB algorithm, the blue curve symbolizes the asymptotically optimal UCB algorithm, and the green curve demonstrates the Thompson Sampling algorithm.

Based on the color notation, the ETC algorithm carried a high slope during the exploration phase, producing a lot of cumulative regrets. Based on Figure 1, when the selected horizon (set at 500) was insufficient for completing the exploration phase, the ETC algorithm exhibited the highest cumulative regrets among all algorithms. For relatively smaller horizons (ranging from 5,000 to 50,000), ETC demonstrated similar cumulative regrets compared to the Thompson Sampling algorithm, occasionally even outperforming it. As the horizon increased, the regret of ETC grew notably due to increased explorations, ultimately surpassing that of the UCB algorithm, and the difference in cumulative regrets comparing to other algorithms became larger as the horizon increased. It has the greatest amount of variance among the algorithms according to Figure 2. The regret of ETC algorithm was also influenced by the length of exploration phase, which was the product of number of arms and user input value m. In condition of horizon being 50,000, when \( m * k \lt 5,000 \) , the maximum average regret of ETC decreased as \( m * k \) increased, and grew up again with \( m * k \) when \( m * k \gt 5,000 \) . This justified that the ETC algorithm performed the best when limiting the exploration phase being \( 10\% \) of the number of rounds each experiment. Hence, ETC algorithm is second-most efficient when choosing the horizon respectively small so the exploration phase can be completed, and it should take exploration phase as \( 10\% \) of the horizon to reach the least regret.

The standard UCB algorithm exhibits its worst performance when selecting a relatively small horizon. It outperforms the ETC algorithm and lags behind the Thompson Sampling algorithm when the horizon is chosen to be greater than a certain value between 50,000 and 100,000. Its advantage, however, when showing the Figure 2, is that its variance is the best among the algorithms. The asymptotically optimal UCB algorithm performed better than the standard UCB algorithm when choosing large input constant of selecting sub-optimal arms, such as \( l = 4 \) . However, it could not outperform the efficiency from choosing smaller input constant, resulting in greater cumulative regret than those of \( l = 2 \) and \( l = 1 \) . Therefore, the standard UCB algorithm could be both efficient and stable when selecting sub-optimal arms rationally. Lastly, although the Thompson Sampling algorithm had a large variance among data according to Figure 2, it had the least cumulative regrets among the algorithms most of the time in the experiment. Hence, as Thompson Sampling algorithm is able to reach the optimal cumulated reward among the algorithms most of the time, the ETC algorithm becomes a favorable option for minimizing cumulative regrets when utilizing a small number of runs and an exploration phase of approximately 10% relative to the total number of runs, and UCB algorithm produces the least variance among them. Also, it is important to notice that the program utilized a random seed that might cause the difference in experiment results. According to previous research, random seed played as an intrinsic factor for the reproducibility of the experiment results in reinforcement learning [8]. Hence, in the future, more experiments with more random seeds can be applied to such experiments for more stable result [9, 10].

4. Conclusion

This study observed the performance of three Multi-armed Bandit algorithms, ETC, UCB, and Thompson Sampling, on the MovieLens dataset to determine the most suitable algorithm for different scenarios. The study simulated different scenarios by changing the input parameters, such as the horizon, the length of exploration phase for ETC algorithm, and the selection of sub-optimal arms for UCB algorithm, to access the performance of each algorithm under different situations. Multiple graphs were drawn by the program to present the cumulative regrets of the algorithms along the experiment. Upon observation, the Thompson Sampling algorithm exhibited the greatest potential for minimizing cumulative regret across most scenarios, while different UCB algorithms demonstrated more stable performance. Furthermore, the ETC algorithm demonstrated superior efficiency compared to UCB when selecting a relatively small number of runs. However, its regrets escalated notably as the number of runs increased, and it necessitated limitations on the exploration phase to attain minimal regret. The future plan would be adapting more experiments with different random seeds to produce more stable result and optimizing efficiency and researching on algorithms that take less time on non-competitive arms.