1. Introduction

With the rise of social media and an exponential growth in mobile app users, the volume of data generated today is staggering. In our increasingly digital world, when data is harnessed ethically and judiciously, it can be pivotal for predictive analytics and enabling tailored recommendations. Within the spheres of data analysis and utility, the multi-armed bandit problem stands out prominently. As a cornerstone of classical reinforcement learning, it fine-tunes decision-making in uncertain scenarios, playing a crucial role in recommendation systems, clinical trials, ad placements, and numerous other domains. This paper zeroes in on two quintessential algorithms associated with the multi-armed bandit problem: the Upper Confidence Bound algorithm and the Kullback-Leibler Upper Confidence Bound algorithm.

Auer et al. (2002) were the pioneers behind the generic Upper Confidence Bound (UCB) algorithm , an optimistic approach crafted to minimize regret by favoring exploration of arms with potentially high rewards. Seeking to refine the assumptions concerning the distribution of rewards, Garivier and Cappé (2011) subsequently introduced the Kullback-Leibler Upper Confidence Bound (KL-UCB) algorithm . This algorithm enhances the UCB by embedding the Kullback-Leibler divergence in the calculation of the upper confidence bound, yielding a more precise estimation of the potential reward for each arm. Although both algorithms have been meticulously dissected in academia, there remains a conspicuous absence of a side-by-side evaluation of their regret performance and inherent complexities. More specifically, in practical applications, an abundance of training sessions can augment their variance, especially when this variance is inherently negligible. This observed lacuna fuels the current investigation, which seeks to juxtapose these two algorithms using a representative movie rating dataset sourced from the Movie Lens Dataset, encompassing user ratings for films. This inquiry endeavors to demystify the practical behavior of the regret performance and complexities inherent to these two algorithms. The revelations from this research endeavor to not only augment the extant understanding of reinforcement learning algorithms but also offer tangible insights for future algorithmic enhancements.

2. Overview of Basic Theory

The field of reinforcement learning, particularly the multi-armed bandit problem, has seen the development and application of various algorithms, including the Upper Confidence Bound and Kullback-Leibler Upper Confidence Bound algorithms. This section provides an overview of the basic theory underlying these algorithms, including their definitions, development, typical applications, and comparative analysis .

2.1. Definition and Development

The multi-armed bandit problem is a foundational scenario in the field of reinforcement learning. The name of this problem originates from a hypothetical situation: a gambler comes to a casino where there is a slot machine with multiple same looking arms. The gambler has certain chances to pull these arms and does not know the probability of winning money from each pull. How should the gambler strategically choose which arms to pull in order to maximize their rewards? In this hypothesis, each "arm" represents a distinct action, and the challenge lies in determining which arms to pull for optimizing overall reward attainment . This necessitates the agent's ability to effectively balance between exploring new options and exploiting existing knowledge, thereby minimizing any potential regrets.

To address this problem, people has developed many basic and improved strategies. The Upper Confidence Bound (UCB) algorithm and the Kullback-Leibler Upper Confidence Bound (KL-UCB) algorithm are two classic and typical algorithms of them. The UCB algorithm, introduced by Auer et al. (2002), is a widely recognized strategy for balancing the exploitation-exploration trade-off in the multi-armed bandit problem. It prioritizes arms with high average rewards and high uncertainty, allowing for efficient exploration of the action space .

The KL-UCB algorithm, proposed by Garivier and Cappé (2011), enhances the UCB approach by incorporating the Kullback-Leibler divergence, a measure of the difference between two probability distributions. The KL-UCB algorithm has been shown to achieve better performance in terms of regret, a metric that quantifies the difference between the reward obtained by the algorithm and the best possible reward.

2.2. Typical Applications

The multi-armed bandit problem and its solutions have found applications in a wide range of fields. In the field of machine learning, they are utilized in reinforcement learning algorithms to effectively manage the exploration-exploitation trade-off . In computer science, they are employed in routing and load balancing algorithms for efficient task distribution among multiple servers.

Specifically in the fields of 5G networks, multi-armed bandit models have demonstrated their utility in resource allocation, small cell planning, distributed resource management, as well as addressing uncertainty and competition . For instance, regarding resource allocation, multi-armed bandit models facilitate optimal utilization of limited spectrum and energy resources particularly under scenarios characterized by significant uncertainty and lack of information.

When UCB and KL-UCB algorithms are applied to online recommendation systems aiming to suggest items (e.g., movies or books) based on users' past behavior, the items can be considered as arms of the bandit while user ratings serve as rewards. The ability of these algorithms to balance exploration and exploitation makes them highly suitable for this task since they can recommend both popular items (exploitation) and less well-known items (exploration) to discover new user preferences.

2.3. Introduction and Definition of UCB and KL-UCB Algorithms

The UCB algorithm statistically estimates the average revenue of each handle through experimental observation. According to the central limit theorem, as the number of experiments increases, the statistical probability converges towards the true probability . In other words, with a sufficient number of experiments, the average payoff approximates the true payoff. The UCB algorithm employs statistical averages instead of true payoffs for each arm. By considering upper bounds on confidence intervals for handle payoffs, arms are sorted and selected based on their highest upper bound value. As more trials are conducted, the confidence interval narrows down and approaches closer to the true value. The following formula are utilized when setting the UCB index for arm \( i \) at round \( t-1 \) .

\( UC{B_{i}}(t-1)={\hat{μ}_{i}}(t-1)+\frac{B}{2}{(\frac{4log{n}}{{T_{i}}(t-1)})^{1/2}} \)

Here, n defines the horizon, B is the difference between the maximum possible reward value and the minimum possible reward value.

The statement "Choose the arm with the largest upper bound on the confidence interval" encompasses several implications: if an arm has a wide confidence interval (indicating uncertainty due to limited selection), it tends to be chosen multiple times, reflecting a riskier aspect of the algorithm. Conversely, if a handle has a narrow confidence interval (suggesting frequent selection and greater certainty), arms with higher means are more likely to be repeatedly chosen, representing a conservative aspect of the algorithm .

The UCB algorithm is an optimistic algorithm, that prioritizes selecting arms based on their ranking according to upper bounds on confidence intervals. Conversely, for those who adopt pessimistic and conservative approaches, choosing lower bounds from confidence intervals would be preferred.

KL-UCB differs from UCB in the use of Chernoff's bound to define the confidence upper bound.

\( {A_{t}}={argmax_{i}}{max{\lbrace \widetilde{μ}∈[0,1]:d({\hat{μ}_{i}}(t-1),\widetilde{μ})≤\frac{log{f}(t)}{{T_{i}}(t-1)}\rbrace }}, where f(t)=1+t{log^{2}}{(t)} \)

The KL-UCB algorithm incorporated the Kullback-Leibler divergence in the calculation of the confidence bounds. This allows the algorithm to have a more refined measure of the uncertainty associated with each arm, thus potentially leading to better exploration-exploitation trade-off .

3. Comparative Analysis of Algorithms

The comparison will be in terms of the expected cumulative Regret an algorithm incurs until round \( t \) , where \( t = 1,...,n \) . Here, n defines the horizon, the total number of rounds the algorithm is used. Each movie genre is an arm, and user ratings are considered as the reward received when movie from a genre is rated by a user.

3.1. Time complexity of UCB algorithm and KL-UCB algorithm

The time complexity of an algorithm refers to the computational resources needed to run it as a function of the size of the input. In the context of multi-armed bandit problems, this can be interpreted as the time required to select an arm to play based on past observations.

The UCB algorithm's time complexity can be viewed as \( O(nT) \) , where \( n \) is the number of arms and \( T \) is the total number of rounds. This is because, in each round, the algorithm computes the upper confidence bound for each arm, a process that takes \( O(n) \) time. It then pulls the arm with the highest upper confidence bound. Since this process is repeated 'T' times, the overall time complexity becomes \( O(nT) \) .

The time complexity of KL-UCB is not as straightforward as UCB's due to the computation of the KL-divergence. The calculation of the KL-divergence for two probability distributions involves a logarithmic function, which is more computationally intense than the linear calculations in UCB. Moreover, finding the KL-UCB index involves solving an equation that usually requires a numerical method such as binary search or Newton's method, each iteration taking \( O(log{T}) \) time. Thus, for each arm and in each round, KL-UCB spends \( O(log{T}) \) time, leading to a total time complexity of \( O(nTlog{T}) \) .

3.2. Performance comparison

The performance of a bandit algorithm is typically evaluated by its cumulative regret, which represents the difference between the rewards obtained and those that would have been obtained if always choosing the optimal arm. Both UCB and KL-UCB demonstrate impressive performance in terms of regret, exhibiting sublinear growth rates that imply approaching zero average regret per round as the number of rounds increases.

The regret values obtained are not the same for each experiment. As shown in Figure 1, that in most cases, the regret value of KL-UCB algorithm is less than the regret value of UCB algorithm. However, the variations of the regret value are about the same.

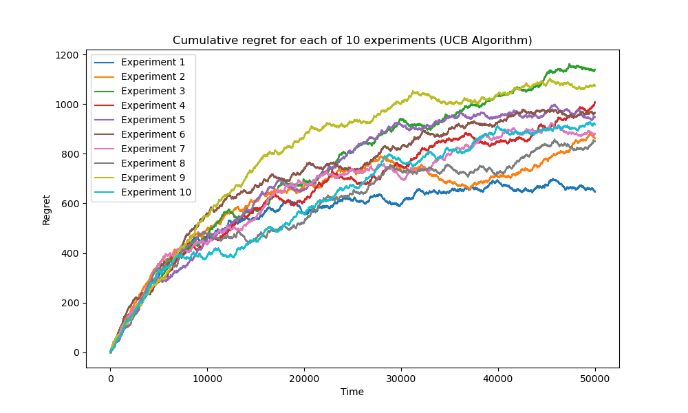
Figure 1. Cumulative regret for 10 experiments (Photo/Picture credit: Original).

The error bars in Figure 2 are the standard deviation of the average regret over 100 experiments for both the UCB and KL-UCB algorithms. It represents variability in the outcomes of our experiments. Although the average regret of KL-UCB is lower, indicating better performance on average, the similar sizes of the error bars suggest that both algorithms have comparable variability.

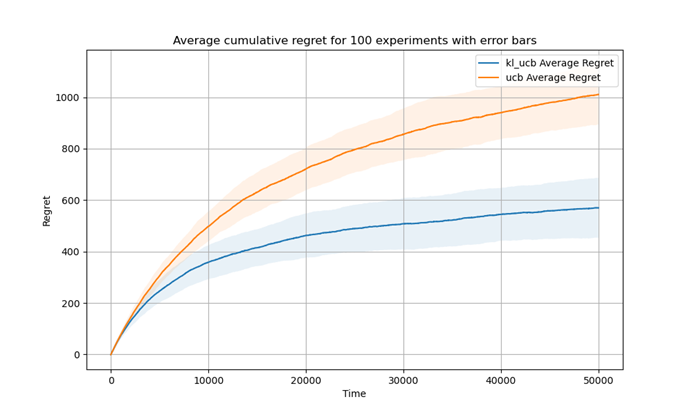
Figure 2. Average cumulative regret for 100 experiments with error bars (Photo/Picture credit: Original).

Actually, both UCB and KL-UCB are designed to address the same problem and employ similar strategies for balancing exploitation and exploration. They both estimate the potential value of each action before selecting the one with the highest value. This similarity in approach could result in comparable variability in their performances. However, there exists a crucial distinction between them. The KL-UCB algorithm employs a more refined measure of uncertainty for exploration, rendering it more cautious and often more efficient in its exploratory actions. Consequently, this typically leads to lower average regret, as observed previously.

Nevertheless, this caution does not necessarily translate into reduced performance variability since several factors can influence it including specific reward distributions within experiments, number of actions available, and total number of steps undertaken per experiment. As a result, similar levels of variability can be observed as indicated by comparable error bars on performance outcomes. Essentially speaking, although KL-UCB tends to outperform UCB on average measures, its range of performance outcomes remains akin to that exhibited by UCB.

Also, when comparing the appropriately of horizon n, two algorithms show different logarithmic regret behavior. The figures 3, 4 and 5 represent the average cumulative regret for 1000 experiments with different horizons (1500, 3000, 7500).

Figure 3. Average cumulative regret for 1000 experiments with horizon 3000 (Photo/Picture credit: Original).

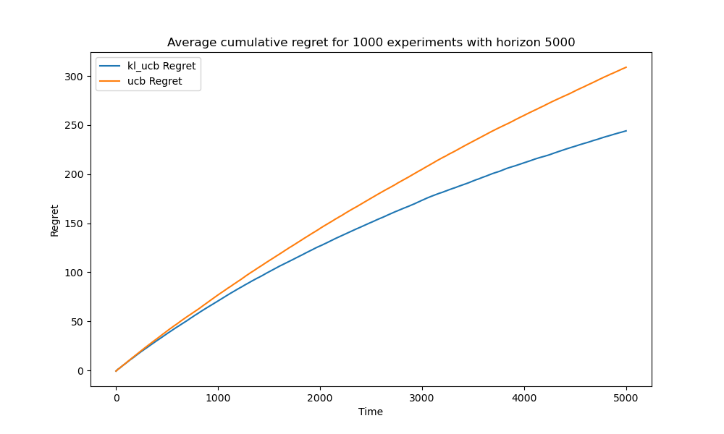
Figure 4. Average cumulative regret for 1000 experiments with horizon 5000 (Photo/Picture credit: Original).

Figure 5. Average cumulative regret for 1000 experiments with horizon 7500(Photo/Picture credit: Original).

When the horizon is set to 1000, the difference between the two algorithms becomes evident. At horizons of 1000 and 7500, the logarithmic regret behavior is apparent for the KL-UCB Algorithm, but only marginally so for the UCB Algorithm.

The KL-UCB algorithm, employing the Kullback-Leibler divergence as its exploration term, takes a more cautious approach to exploration and offers greater precision in estimating the true reward for each action. As a result, KL-UCB showcases superior learning efficiency compared to UCB. With an increase in horizon, KL-UCB's heightened efficiency becomes more pronounced. The cumulative regret starts to exhibit logarithmic growth, signifying rapid identification and exploitation of optimal actions. This logarithmic trend underscores its highly effective learning.

Conversely, the UCB algorithm, which uses a simpler exploration term based solely on the frequency of action trials, provides a balance between exploration and exploitation but often lags in efficiency, especially over extended horizons. In an experiment with a horizon of 5000 steps, UCB's relative inefficiency leads to continued exploration and a more gradual recognition of optimal actions compared to KL-UCB. This difference in cumulative regret growth can be attributed to KL-UCB's sophisticated approach to exploration, enabling faster identification of optimal actions and, consequently, more effective reduction in regret over longer periods.

3.3. Time complexity comparison

The theoretical complexity of both algorithms was previously estimated that the UCB algorithm’s complexity is \( O(nT) \) and the KL-UCB algorithm’s complexity is \( O(nTlog{T}) \) . However, in real applications, the elapsed time of the two runs may be more different. In this experiment, Python was used as the programming language, and the joblib library was used to operate on multiple cores of the CPU to increase the efficiency, and finally a larger difference was obtained. The time taken by the KL-UCB algorithm is huge compared with the time taken by the UCB algorithm and cannot be ignored as well.

To simulate real-world conditions, experiments were run 30 times in parallel on a virtual machine that was allocated 32 CPU cores from one of the highest-performing AMD EPYC™ 9004 Series CPUs, which has a total of 96 CPU cores, under different horizons. Figure 6 shows the relationship between the two in the simulation experiment as a function of the time taken to expand the horizon.

4. Improvements and Challenges

4.1. Overview of possible improvements

In the comparison between KL-UCB and UCB algorithms, it's evident that the KL-UCB algorithm often surpasses the UCB algorithm in various aspects, such as cumulative regret. However, this enhanced performance comes with the trade-off of increased algorithmic complexity, highlighting potential areas for further refinement of KL-UCB and related algorithms.

One potential improvement lies in optimizing the comparison algorithm within KL-UCB. An accuracy comparison experiment, as evidenced by results in Figure 7, indicates that elevating the precision level in the binary search component of the KL-UCB algorithm leads to greater time complexity. Interestingly, the variation and the value of the corresponding cumulative regret don't diminish in tandem. This underlines the importance of identifying a precision level that harmonizes time complexity with the objective of minimizing cumulative regret. Enhancing the algorithm might entail identifying a suitable precision level, possibly by dynamically adjusting the precision based on the algorithm's current state. While this adjustment might primarily lower the time complexity in the algorithm's earlier iterations and potentially increase as the algorithm converges, introducing mechanisms to modify the initiation and cessation of dynamic adjustment could be beneficial. Moreover, in lieu of solely relying on binary search for solving index equations, alternative methods such as interpolation search or exponential search might offer improvements in efficiency, meriting exploration in subsequent research.

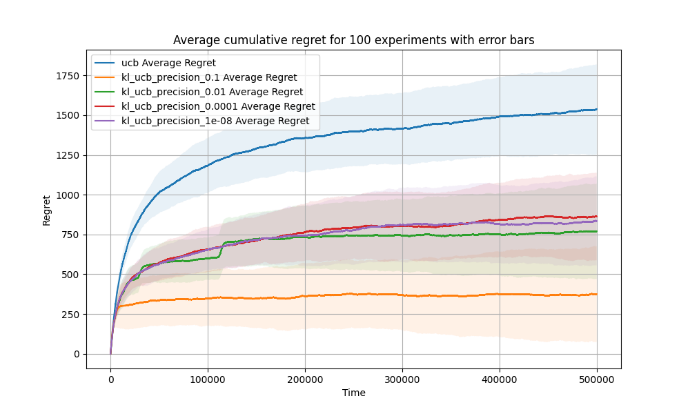
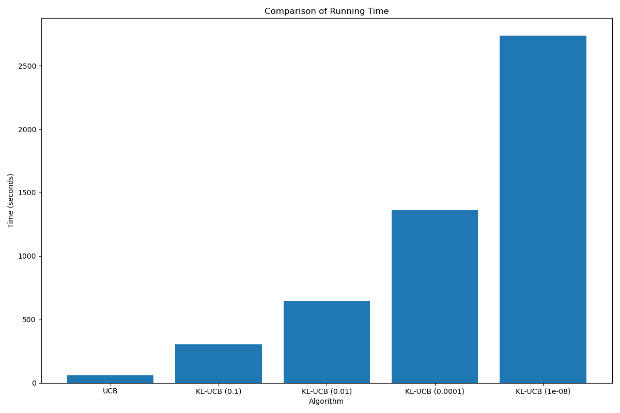
Figure 7. Cumulative regret performance and running time across different algorithms and levels of dichotomy accuracy (Photo/Picture credit: Original).

In addition, the calculation of KL-divergence in the KL-UCB algorithm involves logarithmic and other functions, which requires a large amount of computation, is another area that can be optimized. Approximation techniques such as Taylor series expansion or other types of polynomial approximation can be used to simplify the calculation of KL-divergence. If the reward distribution of arms changes over time, recent rewards can be considered while ignoring outdated rewards through methods like sliding windows.

We can see that in solving large-scale problems such as multi-armed bandits, the performance and computational efficiency of balancing algorithms are particularly important. In these problems, even small efficiency improvements can save a lot of time. While striving to improve performance indicators such as cumulative regret, algorithm design should also aim for computational efficiency. This principle should be given more attention in future improvements and developments of multi-armed bandit problems and similar challenges.

4.2. Discussion in Practice

In practice, artificial intelligence and reinforcement learning are permeating into our lives. However, in most cases, especially when cloud computing cannot be relied upon, the computing power of small terminals is extremely precious and limited. At this point, the complexity of reinforcement learning algorithm is very important. Although some of the algorithms perform poorly on results, their complexity is very low. This allows the terminal to quickly find useful information from a large amount of data with less computing power in a faster time.

For example, in the field of intelligent driving that requires offline operation, sensors can often easily detect a large amount of information data, but the shortcoming is that the processor cannot process all of this information in time, so as to make accurate perception of the farther and wider environment. However, the reality is often that there are a lot of useless data in the information data detected by sensors, and the computing power of the processor is occupied by processing these useless data. This is where less complex algorithms are useful: they may not be accurate, but they can quickly filter out the useful information and feed it back to a more accurate algorithm for processing, thus improving its perception. Better performance may be obtained in practice when the two algorithms with higher and lower complexity are combined into one strategy.

5. Conclusion

This study offers a comprehensive comparison of two hallmark algorithms in the multi-armed bandit landscape: the Upper Confidence Bound and the Kullback-Leibler Upper Confidence Bound algorithms. Emphasis is placed on juxtaposing their theoretical constructs alongside their empirical performance using a movie rating dataset. Both KL-UCB and UCB are tasked with the delicate act of balancing exploration with exploitation. The UCB algorithm boasts linear time complexity, offering efficient computation, consistent performance, and a broad application spectrum. Conversely, the KL-UCB algorithm harnesses the power of Kullback-Leibler divergence, leading to a more nuanced exploration paradigm, which subsequently results in elevated learning efficacy. More often than not, particularly during diverse performance explorations, the KL-UCB outperforms its UCB counterpart. Nonetheless, this superior performance is accompanied by a steeper computational demand. In real-world applications, an array of factors could potentially amplify the time and computational intensity inherent to these algorithms.

These findings unearth invaluable insights for the tangible deployment of these algorithms. While KL-UCB surpasses UCB in areas like regret accumulation, practical implementation calls for a discerning evaluation of the computational demand versus regret performance, contingent on the task at hand. In environments with limited computational resources or those demanding promptness, a synergized approach leveraging streamlined algorithms like UCB could be more advantageous. Although they might not be top performers, their modest computational appetite ensures they remain functional and effective within the system. This exposition also illuminates promising avenues for subsequent research endeavors. The UCB algorithm, for instance, could be enhanced by integrating variance estimation. In parallel, the KL-UCB could either minimize its complexity or elevate its performance by refining its upper confidence bound computation or by implementing a sliding window approach. Future inquiries might also delve into strategies melding both high and low complexity algorithms to optimize real-world outcomes. Ultimately, this analytical exercise underscores the criticality of appreciating the unique merits and demerits of diverse algorithms within the reinforcement learning spectrum. It emphasizes the necessity to judiciously select or refine a pertinent algorithm, tailored to the inherent challenges and demands of a given problem, thus fortifying the performance efficacy of the reinforcement learning algorithm.