1. Introduction

The rise of internet services has been meteoric, with recommendation systems underpinning many of these services. They offer users personalized content, effectively sifting through a deluge of information to present the most pertinent pieces. Such systems are invaluable in assisting users with decision-making [1]. Their pervasive influence can be observed in everyday activities like reading, viewing, listening, or shopping, enhancing the overall user experience. Leading internet giants like Netflix, Spotify, Amazon, and Yahoo leverage these recommendation systems to significant effect. The primary objective of such systems is to heighten user engagement by pinpointing items that resonate with individual preferences. A high-performing recommendation algorithm can discern user predilections with remarkable precision, elevating the overall service quality. Recently, the multi-armed bandit algorithm (MAB) has garnered attention as a promising contender in recommendation system methodologies [2].

Among the myriad of bandit algorithms, the UCB stands out for its versatility. It adeptly strikes a balance between exploration of uncharted optimal choices and exploitation of known ones. By adopting an upper confidence bound strategy, the UCB algorithm narrows its focus on top-performing options while continually scouting for new possibilities. Its appeal lies in its straightforward design, ease of implementation, and minimal parameter tuning, making it a prime choice for real-world applications. Notably, UCB's applicability isn't constrained to specific problem assumptions, rendering it versatile for a spectrum of applications beyond recommendation systems, such as online advertising, medical strategy selection, autonomous vehicle routing, and more.

This paper introduces a recent variation of the UCB, termed the randomized UCB. The goal is to juxtapose the traditional UCB with its randomized counterpart using real datasets, namely MovieLens and Goodreads, to elucidate the pragmatic efficacy of the randomized UCB in tangible settings.

2. Theoretical Overview

Multi-armed bandit problem.

A bandit problem is a sequential game between a learner and an environment.

The game is played over n rounds, where n is a positive natural number called.

the horizon. In each round t∈[n], the learner first chooses an action at from a.

given set A, and the environment then reveals a reward Xt ∈ R [3]. The goal is to find a algorithm maximizing the cumulative reward, which is the highest possible sum of rewards in a series of actions. Regret refers to the difference in expected value between the chosen arm and the optimal arm on each turn. Another way of looking at it is to minimize cumulative regret.

\( {R_{n}}=n*max{μ_{a}}-E[\sum _{t=1}^{n}{X_{t}}] \) (1)

2.1. Classical UCB

The core idea of the UCB algorithm is to select those actions that are estimated to have a high upper bound confidence. The basis of the selection arm of the UCB algorithm is determined by the UCB definition index (which forms a convergent confidence interval) [4]. In each turn, the arm with the highest coefficient is the selected arm. The UCB definition index is.

\( {UCB_{i}}(t-1,δ)=\begin{cases} \begin{array}{c} ∞ if {T_{i}}(t-1)=0 \\ {\hat{μ}_{i}}(t-1)+\sqrt[]{\frac{2log⁡(1/δ}{{T_{i}}(t-1)} } otherwise \end{array} \end{cases} \) (2)

Where δ is called the confidence level and quantifies the degree of certainty for us to choose.

The classical UCB algorithm process [3].

1) Input k and δ

2) for t ∈1,…, n do

Choose action \( {A_{t}}={argmax_{i}}{UCB_{i}}(t-1,δ) \)

Observe reward \( {X_{t}} \) and update upper confidence bounds

3) end for

If \( δ=1/{n^{2}} \) , \( {R_{n}}≤8\sqrt[]{nklog{(}n)}+3\sum _{i=1}^{k}{Δ_{i}} \) thus \( {R_{n}}=O(\sqrt[]{knlog(n)}) \) .

2.2. Randomized UCB

The RandUCB algorithm is a theory-based confidence interval strategy that introduces a random variable Z to use randomization to trade off exploration and exploitation [5]. Its selection index is

\( {i_{t}}=argmax{\lbrace }\hat{{μ_{i}}}(t)+{Z_{t}}\sqrt[]{\frac{1}{{s_{i}}(t）}} \) \( \rbrace \) (3)

where \( {Z_{t}} \) is a uniformly selected discrete distributed random variable for each arm at the t round. \( {Z_{t}} \) is discretely distributed over the interval [L, U], supporting M equally spaced points. If M=1, L=U=β (replace \( {Z_{t}} \) with β when calculating index). \( {Z_{t}} \) can be seen as a random extraction of α1=L, ..., αm = U, αm can be seen as nested confidence intervals. The larger the M, the finer discretization of the underlying continuous distribution supported over the [L,U] interval can be simulated. And \( {s_{i}}(t） \) refers to the total number of times the current arm is selected at round t [6].

3. System Analysis and Application Research

3.1. Comparison of experiments on Movielens

The MovieLens dataset is a public dataset produced by the GroupLens project team. The ratings.dat file contains the user's rating of the movie on a scale of 1-5 [7].

Processing of the MovieLens dataset: 87 films with more than 15,000 reviews were selected as arms in the dataset. The reward is obtained by randomly selecting a score from 1500 evaluations when a certain arm is selected as the reward for that round.

In the specific experiment, we set L and U to 0 and \( 2\sqrt[]{ln{(}T)} \) (T is the totally rounds) respectively for RandUCB algorithm. To prevent \( {s_{i}}(t） \) from being 0, we choose each arm in turn during the first round [8].

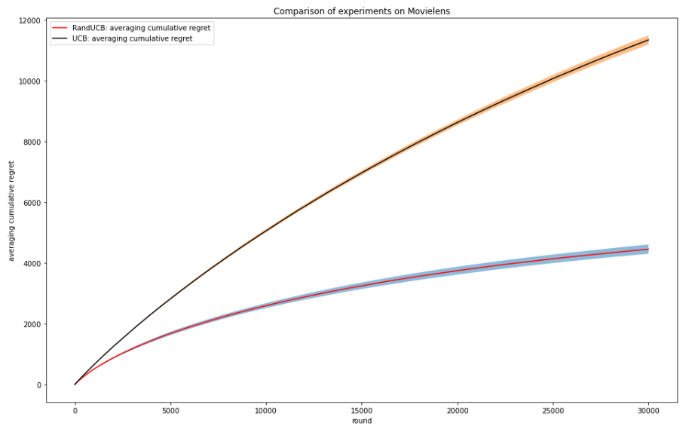
Figure 1. Comparison of experiments on dataset Movielens (Photo/Picture credit: Original).

Figure 1 shows the cumulative regret curves of RandUCB and classical UCB after 100 runs of the system at T=40000. The results show that RandUCB has a slower rate of regret growth than classical UCB, which is consistent with the theoretical results [9]. The transparent bar in the figure indicates the stability of the algorithm. The transparent bar is narrow, and the stability of RandUCB is strong.

3.2. Comparison of experiments on Goodreads

Goodreads is an open access dataset from Internet. It includes 10000 books popular most with 6,000,000 rating data. We use the part of ‘average_rating’, which ranging from 1 to 5 [10]. And we assume the rating each book probably obtain as Bernoulli distribution,

\( p=\frac{\overline{μ}-1}{5-1} \) (4)

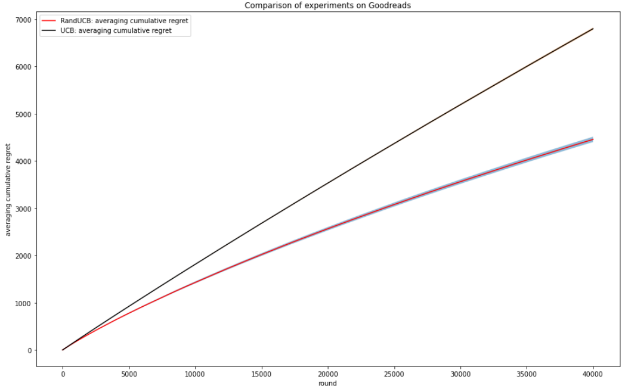
Figure 2. Comparison of experiments on dataset Goodreads (Photo/Picture credit: Original).

Figure 2 shows the results of the cumulative regret curves of RandUCB and classical UCB on the Goodreads dataset after 100 runs of the system at T=40000. The results show that RandUCB has a slower rate of regret growth than classical UCB, which is consistent with the theoretical results. The transparent bar in the figure indicates the stability of the algorithm. The transparent bar is narrow, and the stability of RandUCB is strong.

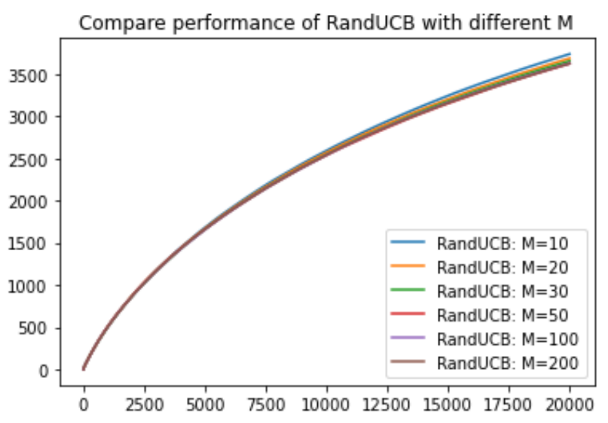
Figure 3. Compare performance of RandUCB with different M (Photo/Picture credit: Original).

Figure 3 shows the cumulative regret curve generated by selecting different M for the RandUCB algorithm after running the system for 100 times when T=40000. The results show that different M has little influence on the results, so there is a large choice of parameter M.

4. Conclusion

In this study, a comprehensive comparison between the Classical UCB and the RandUCB algorithms was conducted, utilizing the MovieLens and Goodreads datasets. Remarkably, the RandUCB, which integrates random numbers into its coefficient selection process, showcased superior performance in real-world recommendation contexts. This was most evident in its cumulative regret curve, which not only exhibited a more gradual growth rate but also maintained consistent stability. An intriguing facet of the RandUCB algorithm is the requirement to select the parameter M. Experimental data indicates that the choice of M exerts minimal influence on RandUCB's performance, offering users a broad leeway in its selection. This flexibility, coupled with its evident efficiency, cements RandUCB's position as an enhanced UCB algorithmic variant. Given these promising results, it's evident that RandUCB holds significant potential for the ever-evolving Internet service industry, particularly within recommendation systems. By employing RandUCB, service providers can elevate the precision of their product recommendations, ensuring a more tailored and satisfactory user experience.