1. Introduction

Over the last two decades, the evolution of data-flow methodologies has seen considerable progress, characterized by breakthroughs in algorithm creation, computational strategies, and diverse applications. The emergence of innovative heuristic and metaheuristic algorithms, including enhanced forms of Genetic Algorithms and Ant Colony Optimization, has brought about enhanced efficiency and adaptability in tackling optimization challenges. The fusion of disparate algorithms to formulate hybrid models has resulted in optimized solutions, amalgamating the advantages of the constituent methods, exemplified by the integration of ILP with heuristics for augmented accuracy and efficacy [1].

The exploitation of multi-core processors and GPUs has propelled the concurrent execution of data-flow algorithms, notably decreasing computational durations and boosting scalability. The incorporation of cloud-centric solutions has simplified the deployment of intricate data-flow algorithms on distributive computational assets, yielding superior flexibility and scalability. Pioneering data-flow mapping methodologies have optimized signal processing in telecommunications, facilitating proficient data conveyance and signal adjustment. In the realm of biomedical signal processing, advanced data-flow strategies have refined medical imaging methods, elevating the precision and dependability of technologies like MRI and CT scans. Data-flow methodologies have also been pivotal in refining financial models, aiding in precise risk evaluation and portfolio structuring.

The convergence of data-flow methodologies with machine learning has optimized learning models, refined feature extraction, and facilitated precise hyperparameter adjustments. Adaptations have been made to these methods to suit the specific requirements of IoT and edge computing setups, optimizing data management and analysis in decentralized frameworks. The creation of sophisticated software tools and platforms has eased the application, examination, and optimization of data-flow methodologies, offering intuitive interfaces and improved visualization features.

Enhanced techniques for evaluating the efficacy of data-flow algorithms have been developed, allowing a more precise measurement of efficiency, scalability, and reliability of these algorithms. Advances in formal methodologies have assured rigorous verification of data-flow algorithms, certifying their accuracy and dependability. Breakthroughs in optimization theories have shed light on the mathematical attributes and convergence tendencies of data-flow methodologies, directing the formulation of more proficient algorithms. These methods have found extensive utility in optimizing manufacturing and logistics, improving productivity and resource allocation.

In the sectors of energy systems and smart grids, sophisticated data-flow methods have been crucial in optimizing energy allocation and utilization, advocating for sustainability and efficacy. The initiation of standardized documentation and best practices has augmented the accessibility and replicability of data-flow methods. The open-source realm has been instrumental in the evolution and propagation of data-flow methods, encouraging mutual cooperation and knowledge exchange among scholars and professionals.

The preceding two decades have seen significant enhancements in data-flow methodologies, with innovations permeating algorithms, computational techniques, applications, and integrations with upcoming technologies. The perpetual evolution in this sector underscores its crucial role in navigating the intricacies and hurdles in varied fields, accentuating its sustained influence in molding the future contours of signal processing, optimization, and related fields.

2. Techniques of data-flow mapping

Data-flow mapping is a prominent methodology applied primarily in software engineering, system creation, and high-level synthesis for delineating, examining, and enhancing the transit and alteration of data within a program or system. This technique is vital for comprehending the manners in which information is processed, altered, and conveyed through various components, facilitating enhancements and optimizations in the overarching software or system architecture.

When applied to system creation and high-level synthesis, data-flow mapping is characterized as the procedure of attributing and coordinating tasks or operations, depicted in a data-flow graph, to resources like memory or processors. This is done while keeping various constraints and objectives in mind, such as reducing execution time, resource utilization, or power consumption. A data-flow graph is a directed graph with nodes symbolizing computations or operations and edges defining the data dependencies among them. This graph is pivotal for data-flow mapping as it visually delineates the manner in which data is transferred and modified between distinct operations or components [2].

Various optimization techniques and problem-solving methods are utilized during the process of data-flow mapping to ascertain optimal outcomes.

2.1. Heuristics and Meta-Heuristics

Heuristics are efficient, uncomplicated strategies, rules, or approaches, formed from experience, which aid in solving problems swiftly when traditional methods are impractical or too time-consuming. They may not assure the best solution but often yield sufficiently effective solutions in practical timeframes. Several algorithms fall under this category.

The greedy algorithm is one such, making locally optimal choices at every step with the aim of discovering a global optimum, illustrated by Prim’s and Kruskal’s algorithms for Minimum Spanning Tree. The Hill Climbing Algorithm selects the adjacent solution that optimizes the objective function, typically employed in optimization problems.

Meta-heuristics are superior-level heuristic algorithms tailored to identify, create, or choose a heuristic that can yield sufficiently good solutions to optimization problems, especially under limitations like imperfect information or computational capacity. The genetic algorithm is a crucial method in meta-heuristics, simulating natural selection processes like mutation, crossover, and selection to find optimal or nearly optimal solutions. Ant Colony Optimization (ACO), motivated by ants’ foraging behaviors, excels in discovering optimal paths through graphs, aiding in solving combinatorial optimization problems such as the Traveling Salesman Problem.

Heuristics and meta-heuristics find applications in operation scheduling, which sequences operations and allocates resources to optimize objectives like minimizing total execution time. They are also instrumental in pathfinding to find the shortest or a reasonably short path in graphs or maps, used in logistical route planning. In game playing, they help formulate strategies or moves, particularly when the search space is too extensive to find an optimal solution promptly. Moreover, they are used in parameter tuning to enhance the performance of a model or a system, as in selecting and tuning machine learning models [3].

While heuristics and meta-heuristics may not invariably yield the optimal solutions, they are essential in tackling intricate problems where other optimization techniques are infeasible or computationally intensive, especially in real-world scenarios with extensive search spaces and multiple constraints, delivering satisfactory solutions in acceptable timeframes.

2.2. Integer Linear Programming (ILP) and Branch and Bound (B&B)

Integer Linear Programming (ILP) serves as a mathematical optimization or feasibility methodology where both the objective function and the constraints are linear, and a portion or all the variables are confined to integer values. As ILP is categorized as NP-hard, obtaining precise solutions can be computationally burdensome, especially with larger problem scales.

To address mapping problems using ILP, certain structured steps must be adhered to. Initially, Formulation is carried out, where the objective function, decision variables, and constraints are defined linearly. Subsequently, the LP relaxation of the ILP is resolved by relaxing the integrity constraints. The final step involves deriving integer solutions from the relaxed solution through rounding or by utilizing strategies like branch-and-bound. ILP finds extensive application in operations research, particularly in areas like scheduling, routing, and resource allocation where decisions are discrete [4].

Branch and Bound is a widely-adopted algorithm mainly used to procure optimal solutions in a variety of optimization problems, including ILP. It explores the solution space systematically, eliminating branches that cannot potentially yield a solution better than the best one identified so far. For effective implementation of Branch and Bound, it is crucial to divide the problem into subproblems, calculate lower and upper bounds for these subproblems, and discard those whose bounds signify they cannot result in an improved solution. It is principally applied in optimization issues, including ILP, the traveling salesman problem, and various combinatorial optimization problems where the solution space is discrete.

In solving ILP, problems are expressed through linear equations and inequalities, with the restriction that decision variables are integers. Strategies like the Cutting Plane Method or Branch and Bound algorithms are often employed to find solutions, carefully navigating the solution space, subdividing it into smaller subproblems, determining bounds for them, and eliminating those that are not promising.

These techniques are essential in circumstances where finding optimal solutions is critical and heuristic methods fall short, such as in high-priority resource allocation or scheduling tasks where the accuracy and dependability of solutions are crucial.

2.3. Constraint Satisfaction Problems (CSP)

Constraint Satisfaction Problems (CSP) are defined as mathematical challenges where a set of objects, each with a specific state, must conform to a series of constraints or restrictions. In CSP, elements are represented as a coherent set of finite constraints over variables, addressed by a constraint solver. The aim in CSP is to find the values of variables that adhere to every given constraint. The foundational components of CSP are Variables, which are the unknown elements to be solved; Domains, depicting the potential values variables can have; and Constraints, which are the conditions the values of the variables must fulfil.

CSP is profoundly utilized in Artificial Intelligence for tasks like spatial and temporal reasoning and is pivotal in solving various real-world industrial dilemmas. It is vital for solving puzzles such as Sudoku and crosswords, as well as for operations like planning, scheduling, and arrangement dilemmas.

To solve CSPs, several algorithms are implemented. Backtracking is a DFS algorithm that aspires to sequentially create a solution, aborting a partial solution (backtracking) the moment it discerns that no conceivable completion of this partial solution exists. Forward Checking is a constraint propagation algorithm that, after a value is assigned to a variable, trims the domain of unassigned variables connected to it by a constraint, ensuring subsequent assignments don’t contradict the current assignment. Constraint Propagation is used in combination with algorithms like Backtracking; it refines the domains of the remaining variables after each assignment, discarding values that are inconsistent with the assignment and narrowing the search space [5].

CSPs are central to computational problem-solving, with applications ranging from puzzles and games to practical planning and scheduling in the real world. Various techniques and algorithms, such as backtracking, forward checking, and arc-consistency algorithms, are employed to derive solutions that satisfy the given constraints. The choice of specific strategies is dependent upon the distinctive requirements and characteristics of the problem being addressed.

3. Application of data-flow algorithms on signal compensation

The influence of distinct algorithms in data-flow mapping techniques in the realm of signal compensation is significantly impactful, holding paramount importance in the efficacy and precision with which signal compensation is executed. This is particularly vital in fields like telecommunications, audio processing, and control systems, where maintaining signal fidelity and exactitude is non-negotiable. Specific algorithms can markedly optimize data-flow, assuring resourceful utilization of available resources and amplifying the overall performance of the system. This is especially critical in real-time systems where the exigency for prompt and efficient signal compensation is crucial to avert delays or any compromise in quality. The selection of a particular algorithm has a direct bearing on the accuracy and meticulousness of signal compensation. Opting for an apt algorithm guarantees minimal error in signal compensation, preserving the integrity of the original signal meticulously. In settings where the conservation of energy is pivotal, such as in devices operated by batteries or in extensive data centers, the chosen data-flow mapping algorithm has a considerable influence on the levels of energy consumption. Employing an algorithm that is efficient in energy consumption extends the life span of devices reliant on batteries and cuts down operational expenses in extensive deployments. The scalability of the algorithm, or its ability to adjust to augmented workload, is indispensable in situations where the magnitude of data processed is subject to fluctuation. An algorithm that scales well ensures the system can manage diverse loads proficiently, maintaining its performance without any deterioration. Therefore, the role of specific algorithms in data-flow mapping methods in signal compensation is crucial, impacting various aspects of signal processing, from accuracy and efficiency to energy consumption and scalability, thus shaping the overall quality and reliability of signal compensation processes. There are some useful algorithms will be introduced in the passage.

3.1. Genetic algorithm

A Genetic Algorithm (GA) is a search heuristic and optimization method inspired by the concepts of genetics and the process of natural selection. This algorithm is especially beneficial for addressing problems where the search space is extensive and lacks a clear understanding. Several components are integral to the functioning of this algorithm.

The population component is pivotal, consisting of all potential solutions, or candidates, for the given problem. This population is subject to genetic processes such as selection, crossover, and mutation, enabling it to evolve through successive generations, aiming to converge towards an optimal solution. Here is an in-depth exploration of the population component in genetic algorithms. The population is a suite of individuals, or chromosomes, each signifying a potential solution to the optimization problem at hand. Every individual in the population is characterized using an appropriate encoding method, typically a binary string. However, other formats like permutations or real-number vectors can be applied based on the nature of the problem. The size of the population delineates the number of individuals in each generation and plays a vital role in determining the efficacy of the GA. A population of insufficient size may lack adequate diversity, risking early convergence, whereas an excessively large one could demand substantial computational resources. The inception population is typically produced randomly, ensuring varied representation within the solution space. In some instances, domain knowledge might be leveraged to populate the initial generation with individuals potentially closer to the optimum solution. Maintaining diversity is indispensable to the evolutionary process, enabling the exploration of varied regions within the solution space, circumventing local minima and early convergence. Several strategies, such as sustaining diverse species (niche), can be used to uphold diversity throughout the algorithm’s iterations. Each member of the population is assigned a fitness value through the fitness function, denoting the proximity of the individual to the optimal solution. This fitness value orchestrates the selection process, determining which individuals are chosen to procreate the subsequent generation. Through generations, due to genetic processes like selection, crossover, and mutation, new individuals are produced, contributing, ideally, to the enhancement of the population’s overall fitness. Selection, crossover, and mutation serve as the essential genetic operators in Genetic Algorithms (GA), facilitating the progression of solutions across generations.

Selection is a mechanism through which individuals from the existing population are chosen to serve as progenitors for the subsequent generation. It aims to prioritize the survival of the most apt by giving individuals with superior fitness values higher probabilities of being selected, enabling them to pass their genetic material to the offspring. Essentially, selection is instrumental in emphasizing the principle of the survival of the fittest by ensuring the propagation of superior genes to succeeding generations. And it is shown in figure 1.

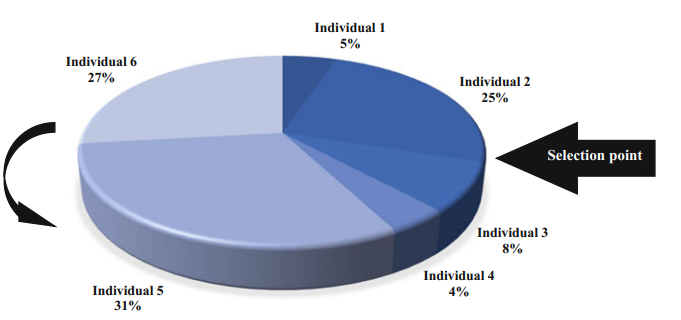
Figure 1. Selection [6].

Crossover is a procedure where genetic information is interchanged between two parent chromosomes, yielding new progeny. This process is crucial as it allows for the synthesis of genetic material from the parents, facilitating exploration and potentially producing more fit offspring by combining advantageous traits from both parents. And it is shown in figure 2.

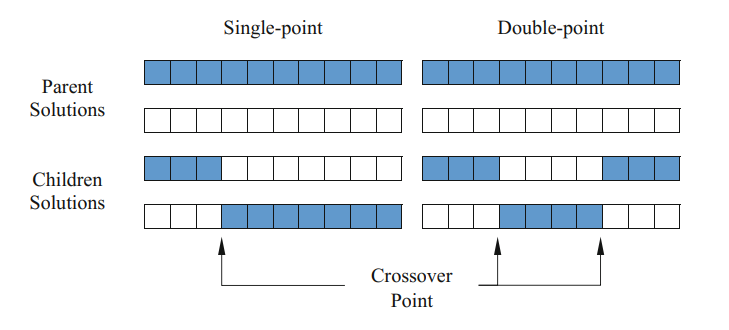
Figure 2. Crossover [6].

Mutation induces random alterations in an individual’s genetic makeup. Its role is to inject genetic variability within the population, granting the algorithm the capability to probe unexplored regions of the solution space and circumvent local optimums. It is pivotal in avoiding stagnation and ensuring sustained exploration of the solution landscape. And it is shown in figure 3.

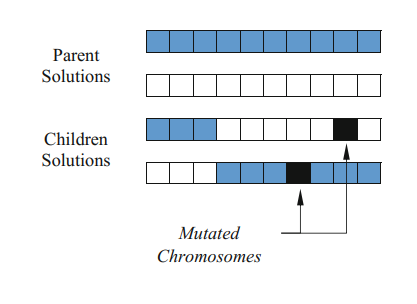
Figure 3. Mutation [6].

The impacts of Genetic Operators are pivotal in genetic algorithms. Selection emphasizes the survival and propagation of the most adapted entities, directing the evolutionary process towards higher-quality solutions by choosing them as progenitors. Crossover facilitates the fusion of genetic information, producing new descendants and thus allowing the exploration of varied areas of the solution space. Mutation induces genetic diversity, preventing the algorithm from prematurely settling on inferior solutions by navigating through new, and possibly better, regions of the solution space. The collective interaction of these elements enables the continuous evolution of the population in Genetic Algorithms, aiding in the scrutiny and utilization of the solution environment to find the most optimal solutions. Maintaining an equitable equilibrium amongst these elements is crucial for optimizing the efficacy of Genetic Algorithms in solving optimization dilemmas [7].

The use of Genetic Algorithms (GA) in signal compensation is illustrated in a scenario where a distorted signal needs rectification or enhancement to align closely with a reference or desired signal. This is valuable in various fields like telecommunications, audio processing, or biomedical signal processing, where an audio signal might be distorted due to noise, interference, or other forms of corruption. The objective in such a scenario is to construct a filter via Genetic Algorithms that can rectify the distortion and recover the original signal as accurately as possible. To address this problem, certain steps need to be executed. The goal is to reduce the error between the compensated (filtered) signal and the original (desired) signal to the minimum. A potential Fitness function is the Mean Squared Error (MSE) between the original and the compensated signals. In this setup, every individual in the population symbolizes a set of filter coefficients.

A population with random coefficients should be initialized. Then, for each individual, implement the filter with its coefficients to the distorted signal and compute the MSE between the filtered and the original signal. Based on their fitness, individuals are selected as parents. For instance, using roulette wheel selection, individuals with lower MSE have a higher probability of selection. Crossover is performed between parent pairs to generate offspring and, consequently, new sets of filter coefficients. Mutation, with a minimal probability, is applied to the offspring, modifying some filter coefficients slightly to discover new potential solutions. The fitness of the newly formed generation is assessed, and it replaces the old one. The evolutionary process is continued for a set number of generations or until the fitness reaches a satisfactory level. Upon the termination of the algorithm, the most optimal set of filter coefficients is extracted and used to process the distorted signal for compensation. Executing the Genetic Algorithm should yield the optimal set of filter coefficients capable of compensating for the distortions in the signal, rendering it as congruent as possible to the original signal.

In conclusion, Genetic Algorithms are adaptable and resilient optimization methods, proficient in discovering solutions within intricate and obscure solution landscapes. In the context of signal compensation, they hold the potential to optimize models or parameters proficiently, allowing for effective signal adjustment. This remains true even when the inherent characteristics and distortions of the signal are intricate and lack clear definition.

3.2. Ant Colony Optimization (ACO)

Ant Colony Optimization is a technique based on probability used to address computational challenges that can be simplified to identifying optimal paths in graphs. It belongs to the family of ant colony algorithms and is modelled after the foraging behaviour of ants as they find a route between their colony and food sources. This algorithm was introduced in the early 1990s by Marco Dorigo, mainly to tackle optimization challenges such as the Traveling Salesman Problem (TSP).

In Ant Colony Optimization (ACO), the Stochastic Search is an essential component where ants (agents) navigate through the solution space, formulating possible solutions by making decisions based on probability at every step. These decisions are influenced by the levels of pheromone and heuristic information. The inherent stochasticity of the search allows for exploration of varied regions of the solution space, aiding in locating globally optimal solutions. Ants progressively construct solutions, selecting the succeeding element (such as a node or edge) to integrate into the current partial solution, relying on probabilistic rules. The likelihood of opting for an element is typically influenced by the pheromone level present on it and, occasionally, additional heuristic information. Stochastic Search in ACO creates equilibrium between exploration and exploitation by establishing a probability distribution over the next nodes, exploring distinct segments of the solution space and averting early convergence to suboptimal solutions. The probabilities are skewed in favor of nodes with elevated pheromone levels and superior heuristic information, enabling ACO to utilize the beneficial regions of the solution space efficiently. The stochastic character of the search, along with the consistent updating of pheromone levels, ensures the exploration of diverse areas of the solution space by different ants. This diversity obstructs the algorithm from stagnating at local minima and encourages the uncovering of a range of high-quality solutions. When a high-quality solution is identified, the paths linked to it receive augmented pheromone deposits, enhancing the probability that ensuing ants will traverse analogous paths and refine the acquired solutions, a phenomenon termed as intensification. The dynamic adaptation of stochastic search in ACO to the modifications in the solution space landscape, driven by the updates in pheromone levels, renders the algorithm resilient and adaptive to the unfolding understanding of the worth of distinct segments of the solution space. And the basic procedures of ant colony optimization is shown in figure 4.

Figure 4. Basic procedures of ant colony optimization [8].

The Pheromone Update mechanism is vital in Ant Colony Optimization (ACO) algorithms, mimicking the natural activity of ants leaving pheromone trails on the paths they follow. This mechanism aims to direct succeeding ants towards optimal solutions by amplifying the appeal of paths that have proven successful. In ACO, the Pheromone Update typically encompasses two primary procedures: Pheromone Evaporation and Pheromone Deposit. In every iteration, a specified proportion of the pheromone on each path dissipates, reflecting the natural degradation of pheromone over time. This evaporation allows the algorithm to progressively “forget” paths that have been explored previously, preventing fixation on inferior solutions. Subsequent to constructing their solutions, ants lay down pheromones on the paths they have traversed. The quantity of pheromone laid is usually correlated with the quality of the solution discovered; superior solutions result in more substantial pheromone deposits. Typically, in problems where the objective is to minimize a cost (such as distance), the pheromone deposited is inversely related to the cost of the solution an ant has discovered. Maintaining equilibrium between pheromone evaporation and deposit is fundamental to sustain a dynamic balance between exploration of new paths and exploitation of known ones. Elevated rates of pheromone evaporation promote exploration but risk the forfeiture of valuable solutions. Conversely, reduced evaporation rates might induce early convergence to inferior solutions. Appropriate levels of pheromone deposit are pivotal in intensifying the search within lucrative areas of the solution space, enhancing the likelihood of finding optimal solutions [9].

Ant Colony Optimization finds utility in signal compensation within the realms of communications and signal processing, specifically to fine-tune the parameters of compensatory filters aimed at counteracting distortions or interference present in received signals. Consider a scenario where a communication system’s signals undergo distortion due to noise and interference while traversing the transmission channel. To rectify the distortions and approximate the original signal with maximum accuracy, a compensatory filter, necessitating optimized parameters, is essential. In employing ACO to ascertain the optimal filter parameters that minimize the discrepancy between the original and the compensated signals, the problem must be construed as an optimization task [10]. The objective here is to pinpoint the filter parameters that most effectively minimize this error. Establish initial pheromone levels across all potential paths (sets of parameter combinations). Each ant within the algorithm formulates a probable solution by selecting filter parameters in a stochastic manner, basing choices on both pheromone levels and heuristic data such as anticipated optimal parameter ranges. The next step involves the evaluation of each formulated solution by applying the chosen compensatory filter parameters to the distorted signal and measuring the resultant error. Pheromone levels are then modified in accordance with the efficacy of the found solutions, where more effective solutions result in higher pheromone deposits. This cycle of solution construction, assessment, and pheromone updates is iteratively performed until predefined stopping criteria, such as a maximum iteration count or acceptable solution quality, are met. Upon conclusion of the algorithm, the most efficacious solution, meaning the optimal set of filter parameters, is extracted for signal compensation. The application of ACO enables the adaptive and intelligent modification of the compensatory filter’s parameters, ensuring superior signal quality and diminished distortions. The optimally derived parameters from ACO can subsequently be integrated into real-time signal processing systems to mitigate signal distortions within communication channels effectively.

Therefore, Ant Colony Optimization offers an organic and understandable analogy for resolving optimization issues, maintaining equilibrium between the exploration and utilization of the solution space via probabilistic choices and pheromone renewal. Its foundational principles of simultaneous processing, positive reinforcement, and retained learning render it a potent and adaptable methodology suitable for a diverse array of optimization challenges.

4. Conclusion

Mapping methodologies for signal compensation bear significant future potential, propelled by ongoing developments in algorithmic approaches and escalating needs in areas such as telecommunications, audio processing, biomedical signal processing, and several other domains. Enhanced and more refined data-flow and control-flow mapping approaches can yield more precise and effective signal compensation. Integrating a variety of mapping and optimization techniques can pave the way for optimal signal compensation strategies, leveraging the benefits of each approach. Advancements in algorithms and hardware are poised to facilitate real-time signal compensation with negligible latency, a vital aspect for domains like telecommunications and audio processing. Adapting in real-time to varying signal conditions and settings will be paramount to uphold signal integrity in fluctuating situations. In summation, the amalgamation of progressive mapping techniques in signal compensation promises expansive future possibilities, including advancements in algorithms, capabilities in real-time processing, applications in nascent technologies, and deployments in diverse areas such as biomedical and environmental signal processing. The convergence of these methods with emerging technological realms like machine learning and quantum computing is anticipated to produce pioneering solutions, addressing the intricacies of contemporary signal environments.