1. Introduction

With the increasing performance of modern GPUs, there is a growing demand for realistic 3D rendering. Global illumination is an effective method for achieving realistic lighting in computer graphics. Traditional real-time rasterization rendering pipelines use advanced algorithms to simulate global illumination.

Screen-space algorithms often sample screen-space coordinates to gather feature information, such as normal and depth, at specific positions. This is done to achieve global illumination effects such as ambient occlusion and reflections. Real-time ray tracing rendering pipelines are constrained by hardware performance and employ a mix of rasterization and ray tracing algorithms. In the ray tracing stage, a limited number of rays per pixel are cast to maintain rendering speed, resulting in noticeable noise in the rendering. Both real-time rendering pipelines share a common characteristic: the need to significantly reduce the number of samples to achieve interactive rendering speeds. The visual effects, such as depth of field and HDR bloom, are common post-processing effects that are implemented using the fuzzy effect. However, these effects can significantly impact the performance of mobile devices. This is because of the characteristics of the tile-based rendering architecture of the GPU, which necessitate multiple reads and writes from system memory to on-chip memory for post-processing.

Mobile devices are more susceptible to power consumption and heat compared to PC devices, and they typically have higher resolutions [1]. Due to bandwidth limitations, the memory usage of textures and the number of texture samples are important factors that impact the power consumption of mobile devices. As the filter kernel size increases, the number of texture samples during rendering also increases. Joint bilateral filtering introduces noise-free feature information but also increases the number of texture samples, which depends on the number of pixels sampled during convolution. Modern GPUs have dedicated texture caches that store neighboring pixels for efficient sampling. However, using large convolution kernels will result in sampling a significant number of pixels outside the texture cache. Frequent cache misses can result in unexpected performance overhead.

The use of convolution filters can be computationally intensive, especially when the filter kernel is large. Real-time denoising of noisy rendering targets at a faster speed and lower cost has been a popular research topic. In real-time rendering, mainstream image processing algorithms first reduce the resolution of the rendering target to an appropriate level and then increase it to the target resolution.

2. Related Work

2.1. Linear filter

Daniel Rákos [2] utilized the characteristics of bilinear sampling to adjust the coordinate offset when sampling textures. This adjustment considers the linear weight of sampled pixels and the Gaussian filter weight. Considering that 2D Gaussian filtering is typically divided into two one-dimensional Gaussian filters to improve performance, Daniel Rákos's method [2] treats each texture sampling as equivalent to two texture samplings, resulting in a 50% reduction in cost.

The Kawase Filter [3] is a high-performance blur algorithm that produces a blur effect like Gaussian blur but with better performance. Utilizing the hardware feature of bilinear sampling, sampling the four pixels diagonally from the target pixel can significantly reduce the number of texture samplings. As the number of iterations increases, the distance between the diagonal pixels and the center pixel also increases. This continuous iteration helps to achieve a faster approximation of a large convolution kernel. Based on the Kawase Filter, the Dual Kawase Filter [4] utilizes down-sampling to decrease computational complexity and achieves anisotropy by employing suitable weights and sampling positions to address the issue of inadequate smoothness in mean blur.

Tianchen Xu [5] proposed a method for approximating large convolutional kernels using box filters. The essence of this algorithm is to compute the approximate weights for each level of the image pyramid and subsequently conduct an up-sampling process using a linear combination approach on the down-sampled image groups. This allows for the fast approximation of linear filters with large convolutional kernels. Tianchen Xu [5] derived weight formulas for box filters that correspond to commonly used filtering kernels in rendering algorithms. These include Gaussian blur for post-processing, irradiance maps for image-based lighting (IBL), and BRDF for ray tracing. The algorithm has key features that include its computational complexity being independent of the kernel size and its cache-friendly nature when implemented on a GPU.

2.2. Non-linear filter

Bilateral filtering is a type of non-linear filtering that considers the influence of the value range in addition to Gaussian filtering. Its purpose is to preserve the edges in the image after filtering. The value range encompasses not only the color of the image, but also feature information such as world space normal, depth, etc., in real-time rendering. These pieces of information are typically stored in rendering textures that have the same resolution as the rendering target. Compared to image color, world space normal and depth are free of noise.

Paris S [6] proposed a signal processing-based method for approximating bilateral filtering. They interpreted bilateral filtering as a high-dimensional convolution and non-linear operation and performed down-sampling of the input image in both the spatial and intensity domains. Then, they conducted convolution operations in the down-sampled space, achieving efficient computation of bilateral filtering. Building on the work of Paris S [6], Jiawen Chen [7] further introduced the concept of bilateral grids.

A novel Gaussian-adaptive bilateral filter (GABF) [8] is proposed by using a low-pass guidance for the range kernel through a Gaussian spatial kernel. GABF attempts to address the issues present in the Gaussian range kernel when filtering input in the presence of noise, as well as its impact on edge-preserving image smoothing operations.

2.3. Deep learning methods

Nowadays, deep learning methods are rapidly developing in various fields, particularly in computer vision [9]. Computer graphics is also experiencing significant advancements in this area. Real-time ray tracing rendering pipelines are gradually starting to integrate deep learning techniques to achieve denoising of the final rendering results. Starting with the proposal of Kernel-Predicting Convolutional Networks [10], there has been a growing number of neural networks introduced for denoising, including the Deep Dual-Encoder Network [11]. However, the time cost of inference using deep learning methods is still unacceptable for real-time rasterization rendering pipelines. In the traditional rasterization process, there are numerous intermediate rendering textures that require blur and denoising processing.

3. Methodology

3.1. Approximation to gaussian filter

Gaussian filtering is a classic low-pass filter, and the resulting filtered image follows a Gaussian distribution. The convolution operation, based on the Gaussian function, applies weights to each pixel in the spatial domain. This can achieve image smoothing or noise suppression. It is commonly used in real-time rendering for post-processing effects, such as depth of field and motion blur.

The Gaussian filter operates on the pixels q in the spatial domain S and calculates the L2 norm of the distance between q and its neighboring pixel p. It then determines the weighted contribution of pixel q to pixel p by applying the Gaussian filter kernel.

Tianchen Xu [5] proposed that when up-sampling, the pixel values obtained from sampling the accumulated up-sampled image and the pixel values obtained from sampling the down-sampled image at the current level are linearly interpolated using the parameters obtained from the weight formula. The formula is as following:

After deduction, Tianchen Xu [5] obtained the Gaussian filter kernel weights, w, corresponding to the box filter. Furthermore, it is possible to derive the linear combination parameter α for the box filter in each layer of the image pyramid. The formula of weight is as following:

Tianchen Xu's method [5] is simple, fast, and suitable for real-time rendering. In addition to fitting the Gaussian filtering kernel, it can also be approximated to calculate computationally intensive functions in real-time rendering. This includes functions like the cosine function for diffuse irradiance maps and microfacet normal distribution functions. Tianchen Xu's method [5] is easy to implement and has practical value. It can be further explored to fit more filters, such as implementing non-linear filters like bilateral filtering based on Gaussian filtering.

3.2. Algorithm pipeline

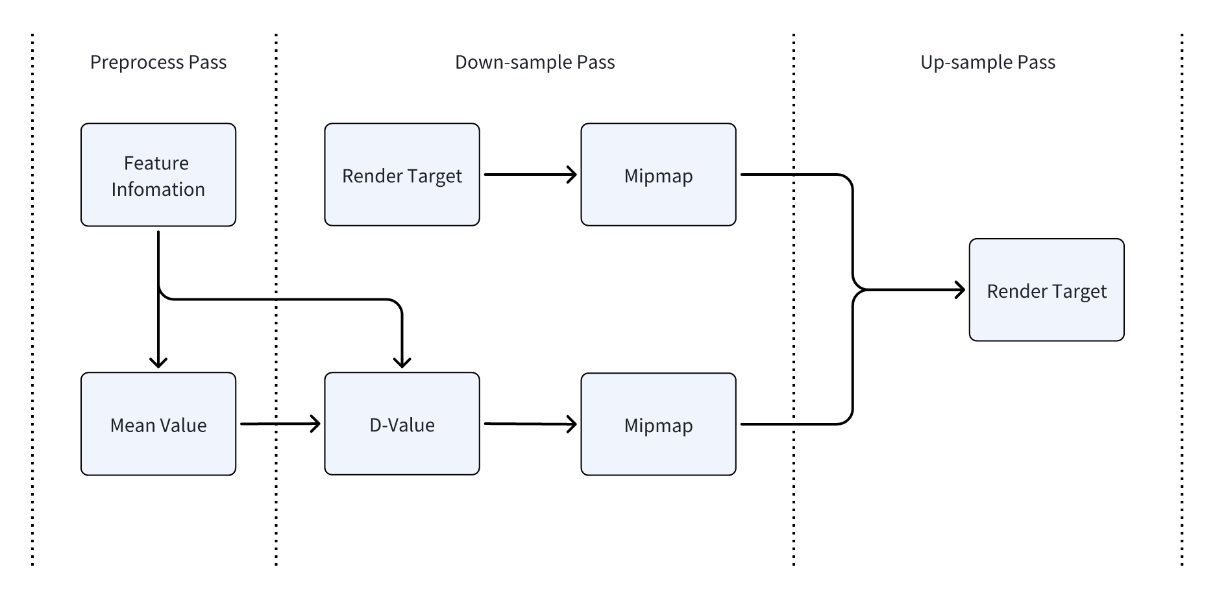
Based on the method proposed by Tianchen Xu [5], we can separate the complexity of the convolution kernel for linear filtering from the sampling frequency. However, in real-time rendering, when implementing bilateral filtering or joint bilateral filtering, multiple texture samples are still required to calculate the range domain weights. These weights are used to compute the value range difference between the sampled pixels and the central pixel. It is evident that the number of texture samples depends on the size of the convolution kernel. To further reduce the large number of texture samples required for computing the value range difference, this paper proposes a differential sampling method based on image pyramids. The algorithm pipeline is presented in Figure 1

(1) To quickly obtain the average of four adjacent pixels for feature images like pixel grayscale, depth, and world space normal, Mipmaps can be generated.

(2) By sampling the original image, we can obtain the original value and the average value using various methods for calculating feature information. These results are then stored in a new rendering texture known as the D-Value Buffer.’

(3) Mipmaps are generated for the D-Value Buffer, corresponding to the pyramid of the original image. The formula is as following:

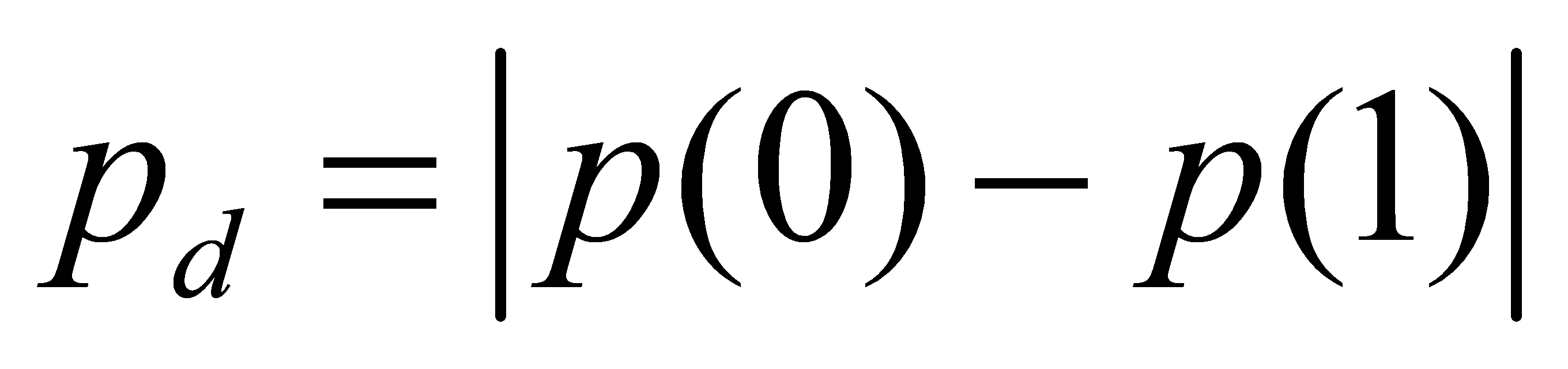
(4) The D-Value Buffer is introduced during fitting, based on the method developed by Tianchen Xu [5]. The difference is sampled according to the level of the image pyramid. After obtaining the difference, we can consider the range weights in the fitting process of the Gaussian filtering in the spatial domain. After calculating the spatial domain weights for this level, the 0-level image pyramid of the down-sampling stage is the original image of the rendered result. The Gaussian filtering approximation result is interpolated with the original pixel based on the range weights.

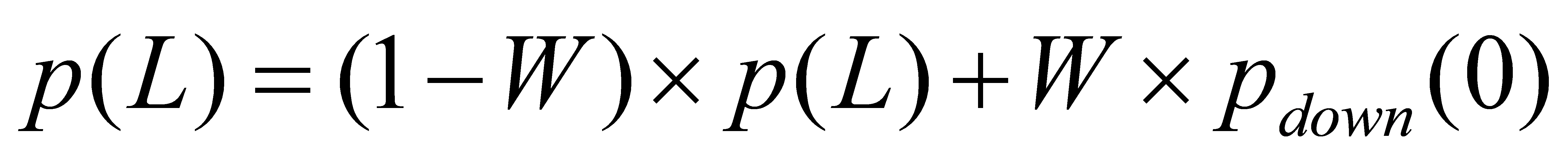
To address the jagged artifacts produced by fitting small-sized convolution kernels with a Gaussian filter in the box filter pyramid, we utilize an algorithm based on the down-sampling technique proposed by Marius Bjorge in the Dual Kawase Filtering [4]. This algorithm samples diagonal pixels during down-sampling and blends them with specific weights.

4. Results

4.1. Tolerance Test

We first implemented Tianchen Xu's method [5] for approximating Gaussian filtering and then implemented bilateral filtering using this method. We conducted tests on Gaussian filtering and bilateral filtering in the Sponza and compared the disparities in the rendered outcomes of the two techniques. It is evident from the tolerance comparison that extending the approximation of non-linear filtering based on Tianchen Xu's method is feasible. The scene rendering is implemented using OpenGL, and the tolerance comparison is tested using Beyond Compare.

The experiment on the Sponza scene with Gaussian filtering demonstrates that the algorithm presented in this paper can successfully simulate bilateral filtering. It can quickly and efficiently sample and calculate value range weights when applying Gaussian filtering at various levels. This allows for the preservation of high-frequency edge signals in the image while minimizing overhead.

4.2. Performance testing

The application of bilateral filtering on the AO map can effectively reduce noise in the AO information without causing excessive blurring at the edges of the AO value range, resulting in outstanding visual effects. In modern pipelines, achieving high-quality screen space ambient occlusion (SSAO)blur is typically done by applying bilateral filtering separately in the horizontal, vertical, and diagonal directions [12]. Taking the implementation of SSAO in the Unity Universal Render Pipeline (URP) as an example, in complex scenes, if down-sampling is not performed, SSAO on iOS and Android platforms requires three rendering passes, resulting in significant overhead from intermediate textures and sampling.

The test scenario involves building with the Unity engine, rendering 1.5 to 2 million triangles within a fixed field of view, and using 1500 to 1800 batches. The scene was packaged as an Android application and tested on the Snapdragon 8+gen1 mobile platform with the results shown in Table 1.

Table 1. Performance testing of different filtering methods for implementing SSAO on mobile devices.

According to the test results, it can be concluded that the bilateral filtering implemented based on Tianchen Xu's method [5] has good performance. It performs equally well as the bilateral filtering implemented after down-sampling by 1/16.

5. Conclusion

In this paper, we extended the method proposed by Tianchen Xu [5] to implement fitting for bilateral filtering. Additionally, we introduced the D-value buffer to reduce the sampling frequency of feature information by down-sampling. However, our method has not yet fully addressed the jagged defects caused by the box filter approximation when using small convolution kernels. Replacing isotropic sampling with mean sampling during the down-sampling process is a feasible approach. In the future, we will explore additional solutions, such as employing a different approximation method that is suitable for small convolution kernels. This will be particularly useful when there are fewer down-sampling levels, as it will help enhance the rendering quality in such scenarios.