1.Introduction

Cancer is a serious disease that can have a significant impact on the physical and mental health of patients [1]. The incidence and mortality rate of cancer are increasing globally. Therefore, predicting the occurrence and treatment effect of cancer has become a research hotspot in the medical field [2,3].

Machine learning algorithms can use a large amount of data and algorithm models to predict the occurrence, development and treatment effect of cancer [4]. This algorithm can learn and find patterns from large amounts of medical data, thereby improving the diagnosis and treatment of cancer. Machine learning algorithms have made some achievements in predicting cancer, but there are still many challenges and problems to be solved [5,6].

Research on machine learning algorithms in predicting cancer has achieved certain results [7]. For example, researchers can use support vector machine (SVM) algorithms to predict the occurrence and progression of breast cancer. This algorithm can learn and find rules from a large number of clinical data and imaging data, thus improving the diagnosis and treatment of breast cancer [8]. Researchers can use Random Forest algorithms to predict the onset and progression of liver cancer. This algorithm can learn and find rules from a large number of clinical data and imaging data, thus improving the diagnosis and treatment of liver cancer [9]. Researchers can use convolutional neural network algorithms to predict the onset and progression of lung cancer. This algorithm can learn and find rules from a large number of clinical and imaging data, thereby improving the diagnosis and treatment of lung cancer [10]. This algorithm can use a large amount of data and algorithmic models to predict aspects of cancer occurrence, development, and treatment effects. In the medical field, machine learning algorithms have been widely used to improve the diagnosis and treatment of cancer.

2.Data set introduction

This dataset is a classic one from the Kaggle competition called "Student Performance Data Set". The dataset contains data on student achievement in two different subjects, mathematics and Portuguese. The data was collected through school reports and questionnaires, which included attributes such as student achievement, demographics, and social and school-related characteristics.

The data set contains several attributes, including students' personal information (such as gender, age, family background, etc.), school information (such as geographical location, school size, etc.), and students' school performance (such as number of absences, homework completion, etc.). These attributes can be used to predict student achievement in math and Portuguese.

The purpose of the dataset is to help educators, policymakers, and researchers understand the relationship between student performance and their background in order to better develop educational policies and improve the quality of education.

For data analysts and machine learning engineers, this dataset can be used to model and analyze student achievement predictions. Various machine learning algorithms, such as linear regression, decision trees, random forests, etc., can be used to predict student achievement in math and Portuguese, and to explore the relationship between student performance and their background.

3.Correlation analysis

Pearson correlation analysis is a statistical method used to measure the degree of linear relationship between two variables. Its principle is based on the concepts of covariance and standard deviation.

Covariance is a measure of whether the trend of change of two variables is the same, and its value is the average of the product of the two variables' respective deviations from their mean. If the change trend of two variables is exactly the same, the covariance is positive; If the trend of change of two variables is completely opposite, the covariance is negative; If the trend of change of the two variables is not related, the covariance is 0.

Standard deviation is a measure of the degree of dispersion of a variable, and its value is the square root of the mean of the sum of squares of the difference between each data point and the mean of that variable. The smaller the standard deviation, the more clustered the data points are near the mean, and the larger the standard deviation, the more dispersed the data points.

The Pearson correlation coefficient is the product of the covariance divided by the standard deviation of two variables, and its value is between -1 and 1. When the two variables are positively correlated, the Pearson correlation coefficient is 1. When the two variables are completely negatively correlated, the Pearson correlation coefficient is -1. When there is no linear relationship between two variables, the Pearson correlation coefficient is 0.

The principle of Pearson correlation analysis is to calculate the covariance and standard deviation between two variables to get the degree of linear relationship between them, so as to judge whether they are correlated.

The data set contains several attributes, including students' personal information (such as gender, age, family background, etc.), school information (such as geographical location, school size, etc.), and students' school performance (such as number of absences, homework completion, etc.). Pearson correlation analysis method was used to calculate the correlation coefficient between each index and draw the correlation heat map. The results are shown in Figure 1 below:

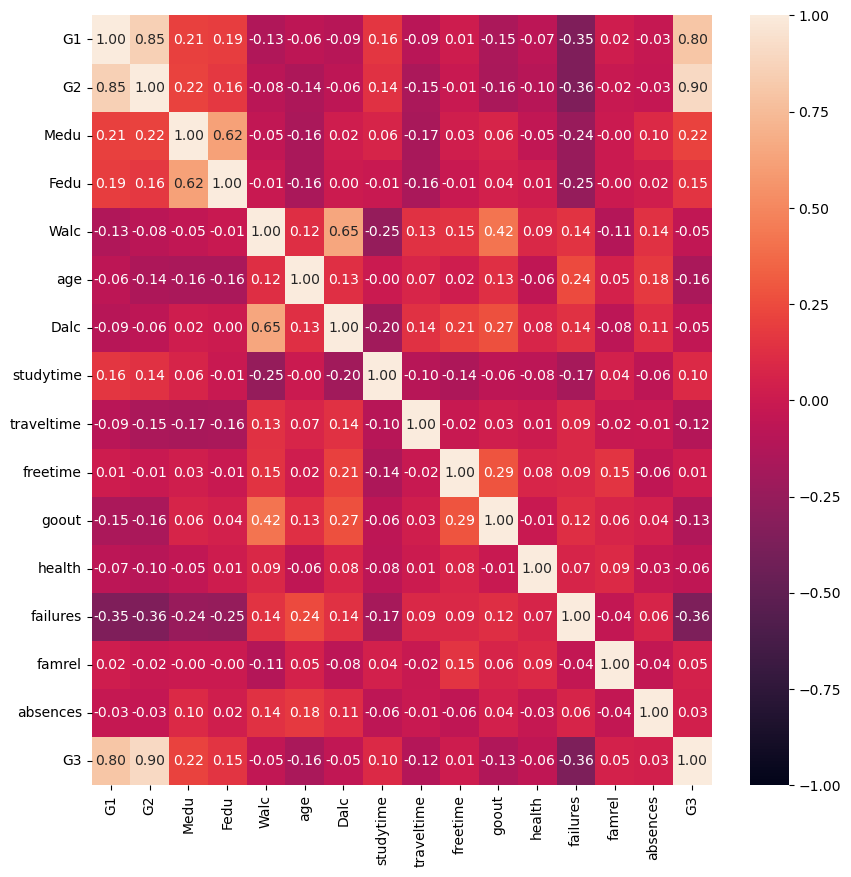
Figure 1. Correlation heat map.

(Photo credit: Original)

4.Method introduction

4.1.Lasso regression model

Lasso regression is a linear regression method widely used in machine learning and statistical modeling. Its full name is Least Absolute Shrinkage and Selection Operator. By adding L1 regularization term to the model fitting process, Lasso regression can realize feature selection and model compression, so as to improve the generalization and interpretation ability of the model.

In Lasso regression, we aim to minimize the residual sum of squares while adding L1 regularization terms. The residual sum of squares refers to the sum of squares of the difference between the predicted and true values, while the L1 regularization term refers to the sum of the absolute values of the coefficient vector w.

The L1 regularization term can compress some coefficients to 0, thus achieving the effect of feature selection. This is because the L1 regularization term is sparse, that is, it tends to change some coefficients to 0, thereby eliminating useless features and improving the generalization and interpretation ability of the model. This feature is especially important in high-dimensional data sets, because the number of features in high-dimensional data sets is often much larger than the number of samples, there are many useless features, Lasso regression can help us to filter out the most important features.

Lasso regression can be solved by optimization algorithms such as coordinate descent method. In practical applications, we can choose the optimal regularization strength alpha value by cross-validation and other methods. It is important to note that when there is multicollinearity between the independent variables (i.e. the independent variables are highly correlated), Lasso regression may randomly select one of the variables while compressing the coefficients of the other highly correlated variables to 0, so in this case we need to use other methods to deal with multicollinearity.

In addition to feature selection and model compression, Lasso regression can also be used in areas such as sparse signal recovery and image processing. In signal processing, Lasso regression can restore the original signal by sparse representation, thus achieving functions such as noise removal and signal enhancement. In image processing, Lasso regression can compress the image by sparse representation, so as to achieve image compression and image denoising. Lasso regression is a very useful linear regression method, which can achieve feature selection and model compression, and improve the generalization and interpretation ability of the model. In practical application, we can choose the appropriate regularization intensity alpha value according to the specific situation, and pay attention to the multicollinearity problem.

4.2.Ridge regression model

Ridge regression is a commonly used linear regression method, which can avoid overfitting problems and improve the generalization ability and stability of the model by adding L2 regularization term in the process of model fitting.

In Ridge regression, we aim to minimize the residual sum of squares while adding L2 regularization terms. The residual sum of squares refers to the sum of squares of the difference between the predicted and true values, while the L2 regularization term refers to the sum of squares of the coefficient vector w. Unlike L1 regularization terms, L2 regularization terms are not sparse and tend to shrink all the coefficients instead of turning some to 0.

The L2 regularization term can avoid overfitting problems because it inhibits the complexity of the model, thereby improving the generalization ability and stability of the model. In practical applications, we can choose the optimal regularization strength alpha value by cross-validation and other methods.

It should be noted that Ridge regression can solve the multicollinearity problem by shrinking the highly correlated coefficients when there is multicollinearity between the independent variables, but it does not compress some of the coefficients to 0, so in the case of feature selection, we need to use other methods, such as Lasso regression.

Ridge regression can be solved by analytical solutions or iterative algorithms. In practical application, we need to choose the appropriate solution method and regularization strength alpha value according to the specific situation.

In addition to its application in linear regression, Ridge regression can also be used in other fields, such as signal processing and image processing. In signal processing, Ridge regression can reduce the influence of noise on signal by regularization, so as to achieve signal enhancement and noise removal. In image processing, Ridge regression can compress images by regularization, so as to achieve image compression and image denoising.

4.3.Elastic Net regression model

Elastic Net is a regression analysis method that combines the benefits of L1 regularization (Lasso) and L2 regularization (Ridge) to improve prediction accuracy in datasets with highly correlated independent variables.

In traditional linear regression, we try to minimize the residual sum of squares (RSS) to fit the model. However, when the independent variables are highly correlated, traditional linear regression may overfit, resulting in poor model generalization ability. In this case, regularization methods can help us solve this problem.

L1 regularization (Lasso) implements feature selection by shrinking some coefficients to 0 and can therefore be used to select important independent variables. However, when the independent variables are highly correlated, Lasso randomly selects an independent variable and shrinks its coefficient to 0, which can cause the model to be unstable.

L2 regularization (Ridge) reduces the coefficients by limiting the sum of squares of the coefficients, which prevents overfitting. However, Ridge cannot be used for feature selection.

Elastic Net combines the advantages of L1 and L2 regularization to control feature selection and overfitting in high-dimensional data sets. Elastic Net is a powerful regression analysis method that improves prediction accuracy in highly correlated data sets, with control for feature selection and overfitting.

5.Result

The data set is divided into the training set, verification set and test set according to the ratio of 6:2:2. The training set is used for model training, the verification set is used for model verification, and the test set is used for model testing, and 50 epochs are trained. The test results are shown in Table 1 and Figure 2:

Figure 2. Model evaluation.

(Photo credit: Original)

The prediction effects of Lasso regression model, Elastic Net model and Ridge regression model are shown in Figure 3 below:

Figure 3. Prediction effects.

(Photo credit: Original)

The results show that Lasso regression model has the lowest prediction error and the best error effect. Elastic Net was the next best predictor, while Ridge regression model had the largest prediction error and was the worst. To sum up, Lasso regression model has the best Performance in grade prediction based on the "Student Performance Data Set" dataset.

6.Conclusion

After analyzing the "Student Performance Data Set" dataset in the Kaggle competition, this paper concludes that Lasso regression model performs best in this dataset and can effectively predict students' achievement in mathematics and Portuguese.

First look at Lasso regression model, Lasso regression is a linear regression model whose goal is to get the best fit by minimizing the objective function. Lasso regression implements feature selection by adding L1 regularization terms to the objective function, which means that it can reduce the coefficients of some irrelevant or unimportant features to zero, enabling automatic feature selection and dimensionality reduction. In the "Student Performance Data Set" dataset, due to strong positive correlations, Lasso regression models can perform best by automatically selecting relevant features to improve prediction accuracy.

Next, let's look at the Elastic Net model. The Elastic Net model is a linear regression model that combines L1 and L2 regularization terms with the goal of obtaining the best fit by minimizing the objective function. The Elastic Net model can achieve both feature selection and dimensionality reduction, and can handle data sets with multicollinearity. In the "Student Performance Data Set" dataset, due to the strong positive correlation, the Elastic Net model can improve the prediction accuracy by using both L1 and L2 regularization terms to control the coefficients of features. Although the Elastic Net model is less predictive than the Lasso regression model, it still performs well.

Finally, we look at the Ridge regression model. Ridge regression is also a linear regression model whose goal is to get the best fit by minimizing the objective function. Ridge regression prevents overfitting by controlling the coefficients of features by adding L2 regularization terms to the objective function. In the "Student Performance Data Set" dataset, due to the strong positive correlation, Ridge regression model may not be able to control the coefficients of features well, resulting in poor prediction results.

In summary, from the perspective of principle analysis of the three models, we can conclude that Lasso regression model performs best in the "Student Performance Data Set" data set, and can improve the prediction accuracy by automatically selecting relevant features. The Elastic Net model is second, and can improve prediction accuracy by using both L1 and L2 regularization terms to control the coefficients of features. However, Ridge regression model has the worst prediction effect and may not be able to control the coefficient of features well, resulting in poor prediction effect. It is important to note that this conclusion only applies to the "Student Performance Data Set" dataset and may be different for other datasets. In practical application, it is necessary to choose the most suitable model and algorithm according to the specific situation.