1. Introduction

In the rapidly evolving field of robotics and autonomous mobility, the intersection of deformable smart car design and PI (Proportional-Integral) control has become a focal point of research and innovation [1]. This convergence is driven by the growing recognition of the critical role these technologies play in disaster response and search and rescue operations.

Recent advancements in deformable smart cars offer a ray of hope in addressing the complex terrains and confined spaces frequently encountered in disaster-stricken areas. These vehicles possess the intrinsic capacity to adapt to challenging environments, making them indispensable tools for mission-critical tasks [2]. However, despite their potential, the practical implementation and optimization of deformable smart cars remain intricate and under-explored.

Simultaneously, PI control has emerged as an indispensable component in the enhancement of smart car behavior, particularly when precise navigation is paramount [3]. The application of PI control mechanisms empowers these vehicles to navigate terrains with unparalleled precision and adaptability [1]. Nevertheless, a comprehensive inquiry into the dynamic interplay between deformable smart car design and PI control integration remains an area ripe for exploration.

This paper aims to delve deeply into this burgeoning domain, seeking to unlock the synergies and potentials hidden within deformable smart car design and PI control. Our research takes a dual-pronged approach: first, to discern the optimal design principles that enable smart cars to expertly traverse intricate terrains, and second, to scrutinize how the integration of PI control mechanisms can elevate their adaptability, responsiveness, and overall stability.

In pursuit of these objectives, our research leverages advanced tools such as SolidWorks for the creation of precise smart car models. These models enable a profound understanding of the intricate physical attributes of these vehicles. Further, simulation platforms like Falstad and Octave are employed to meticulously evaluate the impact of PI control on smart car behavior within controlled virtual environments [4].

The significance of this research transcends its theoretical scope. It promises to inform the future landscape of disaster response and search and rescue operations by empowering practitioners with the knowledge and tools required to optimize deformable smart car performance. Ultimately, this exploration is poised to save lives, minimize damage, and enhance the efficacy of robotic systems in the face of disaster.

2. The mechanical structure of the smart car

The robot consists of two containers and a connecting module equipped with a control circuit. According to Figure 1, an adjacent axis to the connecting module enables it to shift between a "U" shape and an "I" shape, adapting to various terrains and operational requirements. These containers, positioned between the wheels, possess the capacity to transport essential supplies and are outfitted with sensors to fulfill diverse functions [2].

Figure 1. Rendering of 3D modeling. A: Rendering of the Deformable Smart Car in “U” shape; B: Rendering of the Deformable Smart Car in “I” shape.

2.1. Hub Configuration

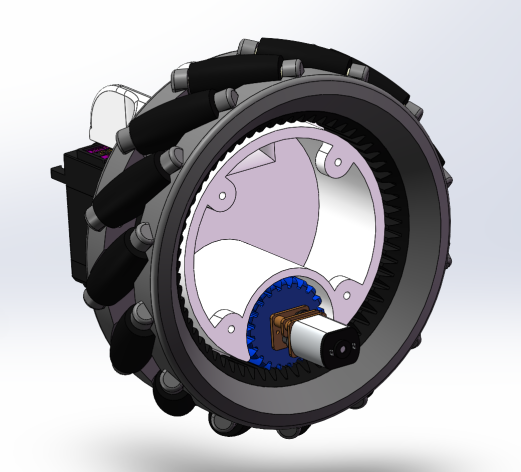
Figure 2. 3D modeling for hub configuration.

The primary rationale behind the hollow hub design of the Mecanum wheel is to enhance maneuverability and facilitate precise motion control, enabling a comprehensive range of movements encompassing forward, backward, translation, and rotation [5]. By diminishing the hub's material usage, the hub's inertial mass can be reduced, thus augmenting its responsiveness and maneuvering capabilities. This heightened responsiveness assumes critical importance when rapid alterations in direction or seamless movements are necessitated. Moreover, the hollow hub configuration simplifies the installation and maintenance of Mecanum wheels [5]. The presence of hollow hubs offers more room, facilitating the easier installation and routing of cables and connectors in and around the hub. Furthermore, the wheels are affixed with 45-degree bearings to attain all-encompassing fixation, enabling omnidirectional mobility.

2.2. Analysis of Shape Transformation for Pipe Navigation

The effective transformation of deformable car into an "I" shape to navigate through pipes marks a significant achievement in enhancing its adaptability to confined spaces. This transformation was made possible by the utilization of MG996R Servo Motors, which enabled the robot to extend its sides, effectively reducing its width and facilitating movement through narrow pipes. This maneuverability showcased the robot's versatility in complex environments.

Throughout the transformation process, the activation of searchlights within the pipes demonstrated the robot's commitment to safety and operational efficiency. Improved visibility within the pipes not only enhanced mission safety but also contributed to more efficient navigation, reducing the likelihood of encountering obstacles.

Upon exiting the pipe, the seamless retraction of the robot's sides to return to the "U" shape is notable. This transition was essential for regaining stability and optimizing operational efficiency after successfully completing the specific pipe navigation task.

The successful execution of shape transformation underscored the synchronized operation of the servo motors and Arduino board. This synchronization ensured precise and timely transformations, emphasizing the effectiveness of the control system in responding to dynamic environmental demands.

2.3. Analysis of Cylindrical Shape Utilization for Downhill Scenarios

A deformable car's capability to transform into an "I" shape and employ a cylindrical configuration for downhill scenarios represents a pivotal development in optimizing its energy efficiency and operational speed. The robot's capacity to adapt its shape by rolling onto its curved bottom surface showcases an intelligent response to varying terrains.

The pivotal role of the control system in determining the necessity of a cylindrical shape based on the terrain demonstrates a high degree of autonomy and adaptability. This real-time decision-making process empowers the robot to maximize its efficiency by reducing energy loss and enhancing stability during downhill movements.

By embracing a cylindrical shape, deformable car effectively minimizes friction and energy consumption, resulting in enhanced operational efficiency during downhill navigation. This capability not only conserves energy but also contributes to improved operational speed, making the robot highly proficient in managing downhill scenarios.

Overall, the successful execution of shape transformation for pipe navigation and the intelligent utilization of a cylindrical configuration for downhill situations highlight deformable car's adaptability and the robustness of its control system, showcasing its potential for diverse applications in challenging environments.

3. Mathematical model of smart car

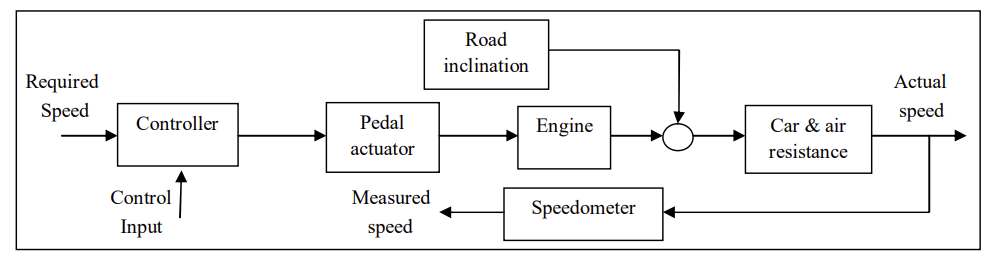
Figure 3. Flowchart for PID control of smart car [6].

Figure 3 illustrates the functional layout of a smart car, demonstrating the measurement of speed, road inclination, and air resistance in conjunction with the controller. Subsequently, the controller initiates appropriate control actions to achieve the desired output.

PI control plays a vital role in smart car navigation by dynamically adjusting the control signals sent to the car's motors or actuators. This adjustment is crucial for maintaining the car's desired trajectory and stability. The impact of PI control on smart cars can be summarized as follows:

In PI control, the proportional component, represented as 'P,' serves to calculate an error signal by measuring the disparity between the smart car's desired and actual positions [7]. Subsequently, it applies a proportional gain to this error, determining the magnitude of the control signal. In practical terms, the 'P' component plays a vital role in ensuring the smart car responds promptly to deviations from the intended path by steering in the appropriate direction. This function is instrumental in reducing oscillations and facilitating a smoother trajectory for the vehicle.

Within the PI control scheme, the integral component, denoted as 'I,' takes on the task of accumulating past error signals and applying corrective measures based on the cumulative error over time. This crucial element helps in rectifying steady-state errors that may arise due to factors such as wheel slippage or external disturbances. In the realm of smart car navigation, 'I' control becomes the linchpin for ensuring that the vehicle eventually reaches and sustains the desired position, effectively eliminating prolonged deviations from the intended path.

The standard PI control system configuration is shown in Figure 4 below.

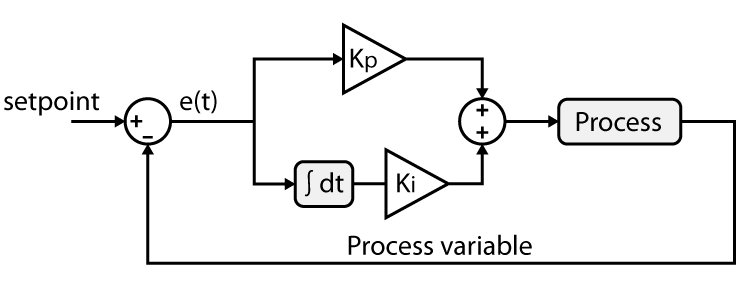
Figure 4. PID control system configuration [8].

According to Figure 4, the control signal is the sum of three terms. \( {K_{p}} \) stands for proportional term and \( {K_{i}}/s \) stands for integral term [4].

The complete PID control signal u(t) is:

\( u(t)={K_{p}}e(t)+{K_{i}}\int e(t)dt\ \ \ (1) \)

where \( {K_{p}} \) is the proportional gain and \( {K_{i}} \) is the integral gain. Thus, the transfer function of the PI controller can be expressed by the formula:

\( \frac{U(s)}{E(s)}={K_{p}}+\frac{{K_{i}}}{s}=\frac{{K_{p}}s+{K_{i}}}{s}\ \ \ (2) \)

3.1. Simulate using Octave

The Octave Matlab code to simulate the above modified PI control system configuration (eq. (1) and eq. (2)) is presented in Appendix A.

The execution of the code generates one plot with three different value of Ki, shown in Figure 5 below.

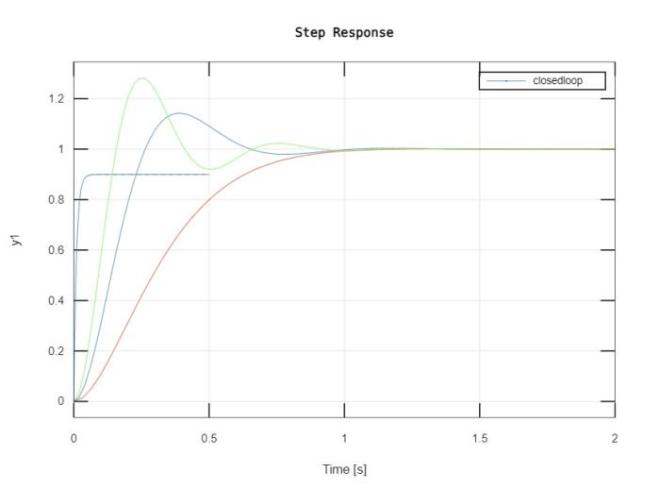
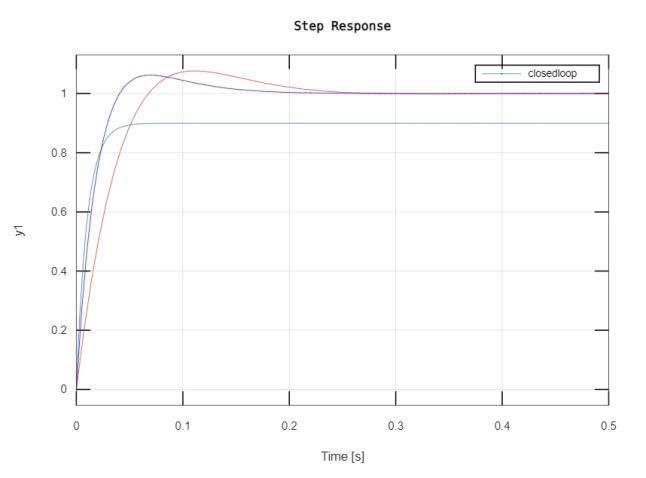
Figure 5. Step Response for PID Closed-loop System by Octave. A: Step Response for different value of Kp; B: Step Response of PI control for different value of Kp and Ki.

From the Figure 5, it can be observed that, increasing the proportional coefficient Kp will generally speed up the response of the system and help reduce the static difference when there is a static difference [7]. However, an excessively large proportional coefficient will cause the system to have a large overshoot and produce oscillation, which will worsen the stability of the system.

Ki, as long as there is an error in the system, the integral effect will continue to accumulate, and the control quantity will be output to eliminate the error. Too strong an integral effect will increase the system overshoot and even cause the system to oscillate.

3.2. Simulate using Falstad

Falstad is used to verify the outcome from the Octave and reveal how PI control is built in the circuit. Figure 6 indicates the layout of circuit of PI control system.

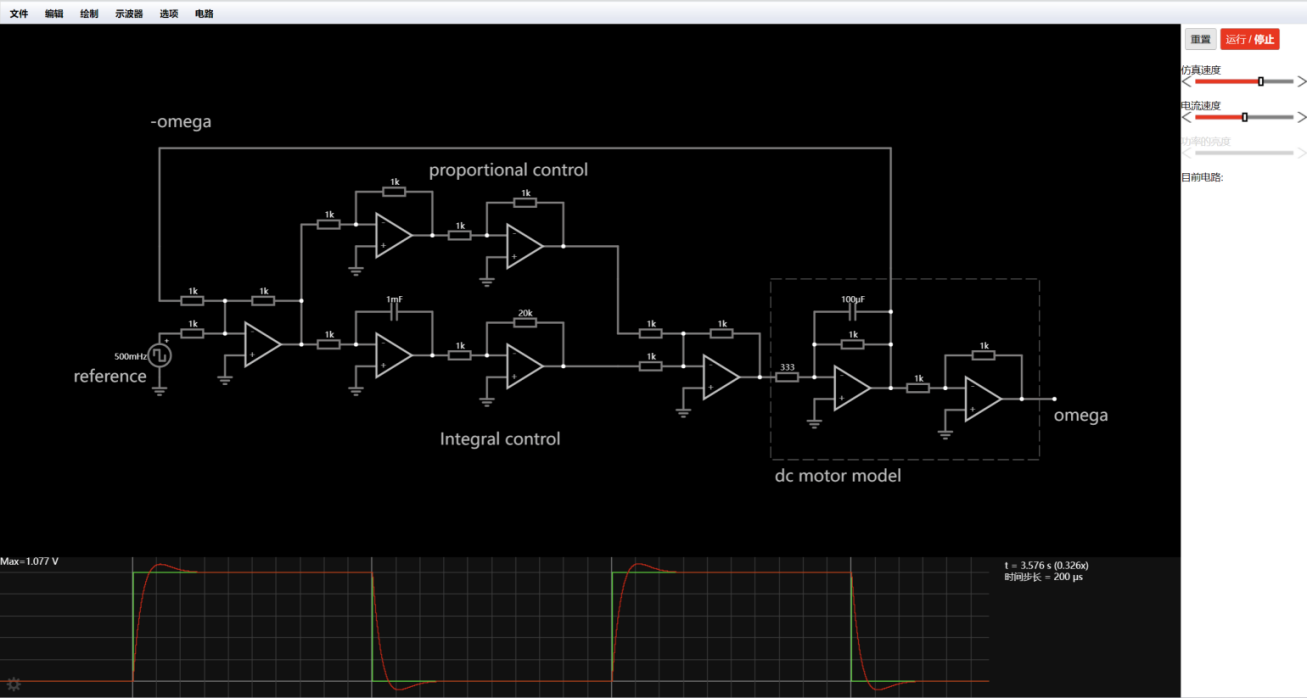
Figure 6. circuit of PI control system in Falstad.

In order to further explore the impact of In order to further explore the impact of Ki and Kp values on the PI system, this report selected different Kp and Ki values for simulation, and the results are shown in Figure 7 below.

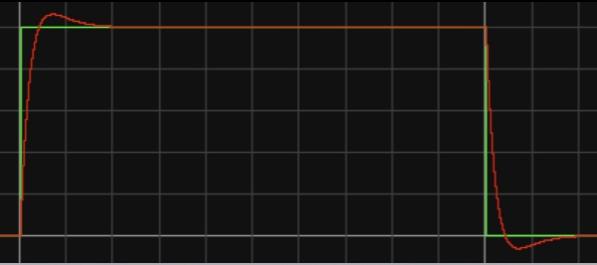
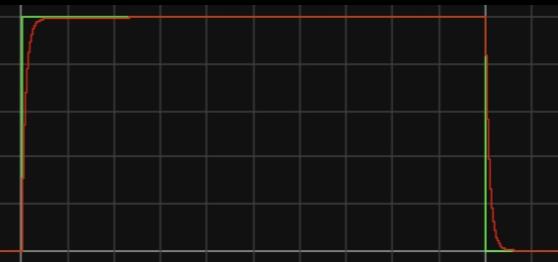
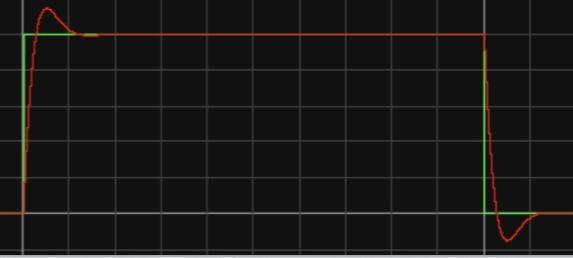
Figure 7. Reference tracking for different value of Kp and Ki in Falstad. A: Reference tracking for Kp=1, Ki=20; B: Reference tracking for Kp=2, Ki=20; C: Reference tracking for Kp=1, Ki=40.

According to figure 7, certain properties can be derived. For Proportional Gain (Kp), Increasing the value of Kp makes the controller respond more aggressively to the current error. This means that the controller will react more quickly to deviations from the desired setpoint, resulting in a faster initial response. However, if Kp is set too high, it can lead to overshoot, where the system's output oscillates around the setpoint before settling. Overshoot can be undesirable in applications that require stability and precision. Conversely, decreasing Kp slows down the controller's response to error, which can reduce overshoot but may also result in longer settling times. Finding the optimal Kp value depends on the specific system and control objectives. It involves balancing Kp to achieve a fast response without excessive overshoot.

For Integral Gain (Ki), it primarily addresses steady-state errors that persist over time. Increasing Ki strengthens the integral action, helping the controller eliminate long-term discrepancies between the setpoint and the actual process variable. However, setting Ki too high can lead to integrator windup, a situation where the integral term accumulates an excessive amount of error. This causes the controller to respond too aggressively when the error starts to decrease, potentially resulting in overshoot and instability. Reducing Ki weakens the integral action, making the controller less effective at eliminating steady-state errors, which may lead to larger steady-state errors in the system's response. Achieving the right balance for Ki is crucial. It should be adjusted to eliminate steady-state errors without causing excessive overshoot or instability.

Kp and Ki often have trade-offs. Increasing Kp for a faster initial response can sometimes lead to an increase in steady-state error, which may be compensated by increasing Ki. However, this should be done cautiously to avoid excessive oscillations or instability. The tuning process typically involves adjusting Kp first to achieve the desired response speed and then fine-tuning Ki to eliminate steady-state errors. This sequential tuning process allows for better control over the balance between responsiveness and precision.

4. Conclusion

This research, at its core, signifies a significant leap forward in the realm of adaptable robotic systems. The integration of deformable smart car design and PI control has unveiled unprecedented potential for enhancing the efficiency, adaptability, and precision of robotic systems. The smart car's capability to transform between "U" and "I" shapes, coupled with its adept navigation through narrow pipes, showcases its versatility and practical utility in complex environments.

Moreover, the intelligent utilization of cylindrical shapes during downhill scenarios highlights the robot's autonomous decision-making capacity and its prowess in conserving energy and improving stability. These features make it a formidable asset in search and rescue operations, disaster-stricken areas, and challenging terrains.

The mathematical model underpinning the smart car's control system, with PI control at its core, illuminates the pivotal role of this mechanism in maintaining trajectory, stability, and precise navigation. Proportional, integral, and derivative components synergize seamlessly, ensuring that the smart car adapts promptly and accurately to external factors.

In summary, the fusion of deformable smart car design, PI control, and shape transformation mechanisms represents a remarkable breakthrough in robotics. This research underscores not only their transformative impact but also their potential to redefine the possibilities of adaptable robotic technology. As we peer into the future, these innovations promise to usher in a new era of robotics, where adaptability, precision, and efficiency converge to address the most pressing challenges in disaster response and search and rescue operations.