1. Introduction

As internet and artificial intelligence technologies rapidly advance, personalized recommendation systems have become increasingly pivotal in daily life. These systems tailor recommendations, from product purchases to news reading, by leveraging users' historical behaviors and preferences [1]. Within this domain, the multi-armed bandit algorithm, a cornerstone of reinforcement learning, has garnered significant interest and research.

Originating from the slot machine metaphor, the multi-armed bandit algorithm equates each 'arm' to a selectable action or strategy, with the 'bandit' representing the encompassing environment. The objective is to maximize rewards or returns through strategic arm selection. The algorithm finds extensive applications across various sectors, including online advertising, finance, medical decision-making, and the smart Internet of Things [2]. This paper focuses on the application and research progress of multi-armed bandit algorithms in music personalized recommendation systems. It begins by elucidating the fundamental principles of key algorithms like Explore-Then-Commit, Upper Confidence Bound, and Thompson Sampling [3]. Subsequently, the application of these algorithms in music recommendation systems is analyzed. This involves comparing the average regret of each algorithm, selecting the most suitable one, and discussing its strengths, weaknesses, and potential optimizations.

The paper concludes by summarizing the main findings of existing research and projecting future research directions and potential applications in this arena. The aim is to provide insights and stimulate innovation in the recommendation system field, offering valuable guidance for researchers and practitioners [4].

2. Principles and Optimization of Typical Algorithms

Before introducing these three specific algorithms, the concept of Multi-Armed Bandit Algorithm needs to be understood. The MAB algorithm is a sequential game between a learner and an environment. A learner can be called a algorithm designer, while an environment reflects the uncertainty in the outcome of the decisions made [5]. Suppose that the game is played over n rounds, and in a single turn \( t \) ( \( t=1,2,3,\ldots,n \) ), the learner has to choose an action (also called an arm) from a set of \( k \) possible actions and receive the corresponding reward \( X_t \) . The learner would like to maximize the cumulative reward over n rounds, i.e. maximize.

\( \ \sum_{t=1}^{n}{X_t=X_1+X_2+\bullet\bullet\bullet+X_n} \) (1)

On the other hand, the quality of choices made can be measured by reward lost by taking sub-optimal decisions. It is called regret value, defined as largest possible cumulative reward in n rounds if the learner knew which arm is the best minus the current situation of the accumulated reward \( \sum_{t=1}^{n}X_t \) . Therefore, the regret value over n rounds becomes [6].

\( R_n=n\bullet\mu^\ast - E\left[\sum_{t=1}^{n}X_t\right] \) (2)

Where \( \mu^\ast\ \) represents the largest mean reward among all arms.

There are also symbols that need to be defined. Suppose there are k possible actions, reward from each action is a Bernoulli random variable. For example, reward from action \( i \) equals zero with probability \( 1 - \mu_i \) , while reward from action \( i \) equals one with probability \( \mu_i \) . So, expected value of the reward from action \( i \) becomes.

\( E\left[Reward\left(i\right)\right]=\mu_i,\ i=1,2,3,\cdots,k \) (3)

If \( \mu_i \) is known beforehand, the optimal policy would be to take the action with the largest mean reward in all rounds, i.e.

\( k^\ast=arg\ {max}\ \mu_i,i=1,2,3,\cdots,k \) (4)

The total expected reward over \( n \) rounds with that choice would be \( n\bullet\mu_k^\ast \) .

In most cases, logarithmic regret is as good as any algorithm can achieve. So-called logarithmic regret means that for some \( C\text{>}0. \)

\( R_n\le C\bullet\log{n\ } \) (5)

2.1. Explore-Then-Commit Algorithm

After introducing the concept definition of Multi-Armed Bandit Algorithm, the specific algorithm will be introduced. The first is the Explore-Then-Commit Algorithm. The core idea of ETC algorithm is to explore by playing each arm a fixed number of times and then exploit by committing to the arm that appeared the best during exploration, which is the same idea as AB testing [7]. During the exploration phase, the learner chooses each arm in a round-robin fashion until all \( k \) arms are selected \( m \) times each. During the commit or exploitation phase, starting with round \( t=mk+1 \) , the algorithm selects the arm with the largest average reward in the exploration phase for all future rounds. Regret value can be calculated as.

\( Regret\ during\ exploration=\sum_{i=1}^{k} ∆_{i}∙m=m∙\sum_{i=1}^{k} ∆_{i} \) (6)

Where \( ∆_{i} \) (sub-optimality gap of arm \( i \) ) \( =\mu^\ast - \mu_i \) , indicating the regret incurred each time the learner selects arm \( i \) .

\( Regret\ in\ commit\ phase=\begin{cases}(n - mk)∆_{1}, if ≥\ max i≠1 {} \\ ⋯ \\ (n - mk)∆_{k}, if ≥\ max i≠k {}\end{cases} \) (7)

Combining, the total mean regret from both phases is given by.

\( E\left[total\ regret\right]=R_n=m\bullet\sum_{i=1}^{k} ∆_{i}+(n - mk)\sum_{i=1}^{k} ∆_{i}∙P(≥\ max j≠1 {}) \) (8)

After a series of simplification, regret value inequality becomes.

\( R_n\le m\bullet\sum_{i=2}^{k} ∆_{i}+(n - mk)\sum_{i=2}^{k} ∆_{i}e^{ - \frac{m∙∆_{i}^{2}}{4}} \) (9)

This term illustrates the trade-off between exploration and exploitation. If the learner chooses \( m \) ‘very large’, the second term is going to be very small since \( e^{ - \frac{m∆_{i}^{2}}{4}} \) is small, i.e., probability of committing to a sub-optimal arm is small. But the first term will be large. However, if the learner chooses \( \ m \) too small, the exact opposite happens [8].

It is assumed that \( k=2 \) (i.e., there are two arms) and \( ∆_{1}=0 \) , \( ∆_{2}=∆ \) . With this simplification, regret value inequality becomes.

\( R_n\le m\bullet∆+(n - mk)∆e^{ - \frac{m∙∆^{2}}{4}} \)

\( \le m\bullet∆+n∆e^{ - \frac{m∙∆^{2}}{4}} \) (10)

\( =m\bullet∆+∆e^{\log{n} - \frac{m∙∆^{2}}{4}} \)

If:

\( \frac{m∙∆^{2}}{4}≥\log{n} \) (11)

Then:

\( e^{\log{n} - \frac{m∙∆^{2}}{4}}≤1 \) (12)

which means that the second term can be made ‘small’ (i.e., less than \( ∆ \) which is the regret incurred by each sub-optimal choice).

Let:

\( m= \) (13)

With this choice, regret becomes.

\( R_n\le\frac{4\log{n}}{∆}+2∆ \) (14)

When horizon \( n\ \) is large, this term will be approximately \( \frac{4\log{n}}{∆} \) .

2.2. Upper Confidence Bound Algorithm

The second one is the Upper Confidence Bound Algorithm. The UCB algorithm is actually generated because the ETC algorithm needs to be improved. The learner uses UCB algorithm so that advance knowledge of the sub-optimality gaps is not needed. Additionally, the abrupt transition from exploration to exploitation is avoided [9]. The UCB algorithm addresses both points and is based on the principle of optimism under uncertainty. Its main idea is that in each round, the learner assigns a value to each arm (called the UCB index of that arm) based on the data observed so far that is an overestimate of its mean reward (with high probability), and then chooses the arm with the largest value. It can be summed up as follows.

\( {UCB}_i\left(t - 1\right)=\widehat{\mu_i(t - 1)}+Exploration\ Bonus \) (15)

Where \( {UCB}_i\left(t - 1\right) \) represents UCB index of arm \( i\ \) in round \( t - 1 \) , \( \widehat{\mu_i(t - 1)}\ \) shows average reward from arm \( i \) till round \( t - 1 \) , exploration bonus indicates a decreasing function of \( T_i(t - 1) \) , \( T_i(t - 1) \) records the number of samples obtained from arm \( i \) so far. So, the fewer samples for an arm, the larger will be its exploration bonus. It is worth noting that being optimistic about the unknown supports exploration of different choices, particularly those that have not been selected many times.

There is another concern about how to choose the exploration bonus. It should be large enough to ensure exploration but not so large that sub-optimal arms are explored unnecessarily. The following confidence bound will guide the choice of the exploration bonus. Let \( \left\{X_t,t=1,2,\cdots,n\right\} \) be a sequence of independent \( 1 - subGaussion\ \) random variables with mean \( \mu \) . Let

\( \mu=\frac{\sum_{t=1}^{n}X_t}{n} \) (16)

Then,

\( P\left(\hat{\mu}+\sqrt{\frac{2\log{\frac{1}{\delta}}}{n}}\text{>}\mu\right)\geq1 - \delta\ for\ all\ \delta\in(0,1) \) (17)

Where \( \hat{\mu}\ \) indicates empirical average over \( n \) samples, \( \sqrt{\frac{2\log{\frac{1}{\delta}}}{n}} \) is the term added to the average to overestimate the mean, \( \mu \) shows true value of the mean. So, if the learner chooses \( \hat{\mu}+\sqrt{\frac{2\log{\frac{1}{\delta}}}{n}} \) as the UCB index for an arm that has been selected \( n \) times, then this index will be an overestimate of the true mean of that arm with a probability of at least \( 1 - \delta \) . \( \delta\ \) should be chosen ‘small enough’ and it will be chosen \( \delta=\frac{1}{n^2}. \) Therefore, \( \sqrt{\frac{2\log{\frac{1}{\delta}}}{n}} \) is selected as the exploration bonus for an arm that has been selected \( n \) times.

After the above analysis, the specific steps of the UCB algorithm can be summarized as follows. Firstly, input \( k\ \) and \( \delta \) . Secondly, for \( t=1,2,\cdots,n \) , choose action \( A_t={arg}_i\max{{UCB}_i(t - 1,\delta)} \) . Thirdly, observe reward \( X_t \) and update the UCB indices. Finally, end for where the UCB index is defined as.

\( {UCB}_i\left(t - 1,\delta\right)=\widehat{\mu_i(t - 1)}+\sqrt{\frac{2\log{\frac{1}{\delta}}}{T_i(t - 1)}} \) (18)

If \( T_i\left(t - 1\right)=0\ \) (i.e., arm \( \ i \) has never been selected until round \( t - 1 \) ), then \( {UCB}_i=\infty. \) This equation ensures that each arm is selected at least once in the beginning.

The performance of the UCB algorithm is dependent on the confidence level \( \delta. \) For all arms \( P({UCB}_i\le\mu_i)\le\delta \) at any round. So, \( \delta\ \) controls the probability of the UCB index of an arm failing to be above the true mean of that arm at a given round. The learner does not want this to happen at any one of the n rounds. So, choosing \( \delta\ll\frac{1}{n} \) will ensure that the probability of UCB index ‘failing’ at least once in \( n \) rounds is close to zero. A typical choice would be \( \delta=\frac{1}{n^2} \) . With this choice, the equation becomes.

\( {UCB}_i=\widehat{\mu_i(t - 1)}+\sqrt{\frac{4\log{n}}{T_i(t - 1)}} \) (19)

The corresponding UCB algorithm is sometimes referred to as \( {UCB}_1 \) .

However, there are two caveats with the previous UCB algorithm where \( \delta=\frac{1}{n^2} \) . On the one hand, it requires the knowledge of horizon \( n \) (algorithms that do not require the knowledge of \( n\ \) are called anytime algorithms) [10]. On the other hand, the exploration bonus does not grow with \( t \) , i.e., there is no built-in mechanism to choose an arm that has not been selected for a long time. To solve these problems, Asymptotically Optimal UCB Algorithm is introduced. In rounds \( t=k+1 \) , the learner chooses \( A_t={arg}_i\max{(\widehat{\mu_i(t - 1)}+\sqrt{\frac{2\log{(f(t))}}{T_i(t - 1)}})} \) where \( f\left(t\right)=1+t\log^2(t) \) . So, the exploration bonus is modified as \( \sqrt{\frac{2\log{(1+t\log^2(t))}}{T_i(t - 1)}}) \) . The UCB index is updated at every round for all arms. Exploration bonus increases for arms not selected, and decreases for the selected arm. Comparatively, exploration bonus of the UCB algorithm \( \sqrt{\frac{4\log{n}}{T_i(t - 1)}} \) remains the same for the arms that are not selected, and goes down for the selected arm.

2.3. Thompson Sampling Algorithm

The third one is Thompson Sampling Algorithm. It is based on Bayesian Learning. The uncertainty in the environment is represented by a prior probability distribution (reflecting the belief on the environment). Then, the learner chooses the policy that minimizes the expected loss. For example, let \( \varepsilon \) denote the set of all possible environments. For each possible environment \( v \) , let \( q(v) \) denote the possibility that the environment is \( v \) . Then, the optimal policy is given by \( {arg}_\pi min\sum_{v\in\varepsilon}{q(v)}\bullet l(v,\pi) \) , where \( l(v,\pi) \) means the loss of \( \pi \) under environment \( v \) , \( \sum_{v\in\varepsilon}{q(v)}\bullet l(v,\pi) \) means expected loss of policy \( \pi \) .

In the sequential decision-making framework (e.g., multi-armed bandits), the learner can update the prior distribution on the environment based on the data observed in each step, and make the next decision using the new distribution. The new distribution (computed after data is obtained) is called the posterior.

The main idea of Thompson Sampling Algorithm is using Bayesian Approach. The learner starts with a prior distribution (e.g., on the mean reward of each arm), makes a decision based on the current distribution of mean rewards, and gets new data. Then, the current distribution is updated by using new data. A key difference with other algorithms covered is that exploration in TS algorithm comes from randomization. In addition, Thompson Sampling Algorithm is shown to be close-to-optimal in a wide range of settings. It often exhibits superior performance in experiments and practical settings compared to UCB and its variants. However, it can have larger variance in its performance from one experiment to the next.

After the above analysis, the specific steps of Thompson Sampling Algorithm can be summarized as follows. Firstly, input prior cumulative distribution function (CDF) \( F_1\left(1\right),\ F_2\left(1\right),\cdots,F_k\left(1\right) \) . These reflect the belief on the mean reward of the arms. Secondly, for \( t=1,2,\cdots,n \) , sample \( \ \theta_i~F_i(t) \) independently for each arm \( i \) . Thirdly, choose \( A_t=arg{max}_i\theta_i(t) \) . Then, observe \( X_t\ \) and update the distribution of the arm selected in the third step. Let \( F_i\left(t+1\right)=F_i\left(t\right) \) for all \( i\neq A_t \) because the distribution remains the same for the arms that have not been selected. Comparatively, \( F_{A_t}\left(t+1\right)=UPDATE(F_{A_t}\left(t\right))\ \) . For the arm selected in round \( t \) , the CDF of its mean reward is ‘Bayesian-Updated’ using the new data \( X_t. \) In most implementations of this algorithm, Gaussian UPDATE is used:

\( UPDATE\left(F_i\left(t\right),A_t,X_t\right)=CDF(N(\widehat{\mu_i\left(t\right)},\frac{1}{T_i(t)})) \) (21)

This means that the ‘current belief’ about the mean reward of arm \( i \) is represented by a Gaussian distribution with \( mean=\widehat{\mu_i\left(t\right)}=average\ reward\ received\ from\ arm\ i\ until\ round\ t \) and \( variance=\frac{1}{T_i(t)}=\frac{1}{number\ of\ samples\ from\ i\ till\ round\ t} \) . Variance decreases as \( T_i(t) \) increases. If the reward distributions are \( \sigma - subGaussian \) , it becomes \( CDF(N(\widehat{\mu_i\left(t\right)},\frac{\sigma^2}{T_i(t)})) \) .

3. Applications in music recommendation system

3.1. Spotify System Context

Music recommendation systems have become increasingly popular as more and more people rely on digital platforms for their music consumption. These systems aim to provide personalized recommendations to users based on their preferences and past listening behavior. Spotify is one of the typical examples.

Spotify’s mission is to unlock the potential of human creativity — by giving a million creative artists the opportunity to live off their art and billions of fans the opportunity to enjoy and be inspired by it. It aims to match fans and artists in a personal and relevant way.

Developers have put a lot of effort into this goal, such as the design of the home page. Home is the default screen of the mobile app for all the users worldwide. It surfaces the best of what Spotify has to offer, including music and podcasts for every situation, personalized playlists, new releases, old favorites, and undiscovered gems. Value to the user here means helping them find something they’re going to enjoy listening to, quickly.

At the core of Spotify's mission lies the ambition to empower human creativity----embarking on a journey to support a myriad of talented artists in realizing their dreams, while simultaneously providing billions of fans with the opportunity to revel in and draw inspiration from their creations. Central to achieving this objective is the seamless alignment between enthusiasts and creators, fostered through a personalized and meaningful connection.

This lofty goal has driven developers to dedicate significant resources, particularly evident in the meticulous design of app's home page----the quintessential entry point for the global user base. Here, users are greeted with a curated selection showcasing the very essence of Spotify's offerings. From an eclectic mix of music and podcasts tailored to every mood and moment, to personalized playlists catering to individual tastes, and a treasure trove of both new releases and timeless classics, the home page is a gateway to an unparalleled auditory experience.

The relentless pursuit of value for the user is epitomized in the commitment to facilitating swift and enjoyable content discovery. Whether it's uncovering a new favorite track or diving into a hidden gem, its endeavor is to ensure that every visit to the home page is met with a delightful and fulfilling musical journey.

3.2. Algorithm Implementation

Among the various algorithms used in music recommendation systems, the Explore-Then-Commit (ETC) algorithm has gained attention for its unique approach to balancing exploration and exploitation.

In the context of music recommendation, the ETC algorithm introduces a two-phase approach. Initially, it focuses on exploring a wide range of songs or artists to gather information about user preferences. This exploration phase allows the algorithm to build a diverse understanding of the user's music taste. After the exploration phase, the ETC algorithm transitions into the exploitation phase, where it leverages the knowledge gained during exploration to provide personalized recommendations. By committing to the best-performing songs or artists identified during exploration, the ETC algorithm ensures that the recommendations align with the user's preferences.

The advantage of the ETC algorithm is its ability to adapt to changing user preferences over time. By periodically re-evaluating the performance of recommended items, the algorithm can update its understanding of the user's preferences and adjust future recommendations accordingly.

The other popular algorithm used in music recommendation systems is the Upper Confidence Bound (UCB) algorithm.

In the context of music recommendation systems, the UCB algorithm helps suggest songs or artists to users by effectively managing the trade-off between recommending familiar tracks that the user is likely to enjoy and recommending new tracks to explore. The UCB algorithm works by maintaining an estimate of the expected reward associated with each song or artist. It leverages a confidence bound to determine the degree of exploration or exploitation for each recommendation. By continuously updating the estimates based on user feedback, the UCB algorithm adapts to individual user preferences over time, providing more accurate and personalized recommendations.

The UCB algorithm's ability to strike a balance between exploration and exploitation makes it an ideal choice for music recommendation systems. It allows users to discover new music while also ensures that their preferences are taken into account. Additionally, the UCB algorithm's adaptability and scalability make it suitable for large-scale music recommendation platforms that handle vast amounts of user data. It plays a significant role in enhancing the user experience of music recommendation systems by providing personalized and diverse recommendations that cater to individual preferences while encouraging exploration and discovery.

The other algorithm that has gained attention for its effectiveness in these systems is the Thompson Sampling algorithm.

In the context of music recommendation, the Thompson Sampling algorithm operates by maintaining a probability distribution over the potential songs or artists to recommend. It dynamically updates this distribution based on user feedback, constantly adapting to individual preferences.

The key advantage of the Thompson Sampling algorithm lies in its ability to balance exploration and exploitation. It achieves this by using a Bayesian approach, where it samples from the probability distribution to select recommendations. This allows the algorithm to explore new songs or artists while also exploiting the knowledge gained from past user feedback. The Thompson Sampling algorithm's adaptive nature makes it particularly effective in music recommendation systems. It continuously learns and updates its understanding of user preferences, ensuring that recommendations become more accurate and personalized over time.

Another advantage of the Thompson Sampling algorithm is its ability to handle uncertain environments. In music recommendation systems, where user preferences can vary and evolve, this algorithm excels by adapting to changing tastes and providing recommendations that suit individual users' preferences.

The scalability of the Thompson Sampling algorithm also makes it suitable for large-scale music recommendation platforms. It can efficiently handle vast amounts of user data, making accurate recommendations even in high-demand scenarios.

3.3. Results Analysis

To optimize the personalization of user experiences and foster meaningful connections between fans and artists, the author has opted for a sophisticated database encompassing a wealth of user information. This comprehensive dataset includes factors such as gender, age, historical listening patterns, preferred genres, and more. Each music genre within this database serves as an 'arm' within the context of Multi-Armed Bandit (MAB) algorithms, while user ratings represent the rewards garnered when a user engages with music from a particular genre.

The performance evaluation of various MAB algorithms, like Explore-Then-Commit (ETC), Upper Confidence Bound (UCB), and Thompson Sampling (TS), is crucial in determining their efficacy in this context. This assessment revolves around measuring the expected cumulative Regret incurred by each algorithm up to round \( t \) , where \( t \) ranges from \( 1 \) to \( n \) , defining the total number of rounds the algorithm is deployed.

By running the code, the result looks like the Figure 1-4.

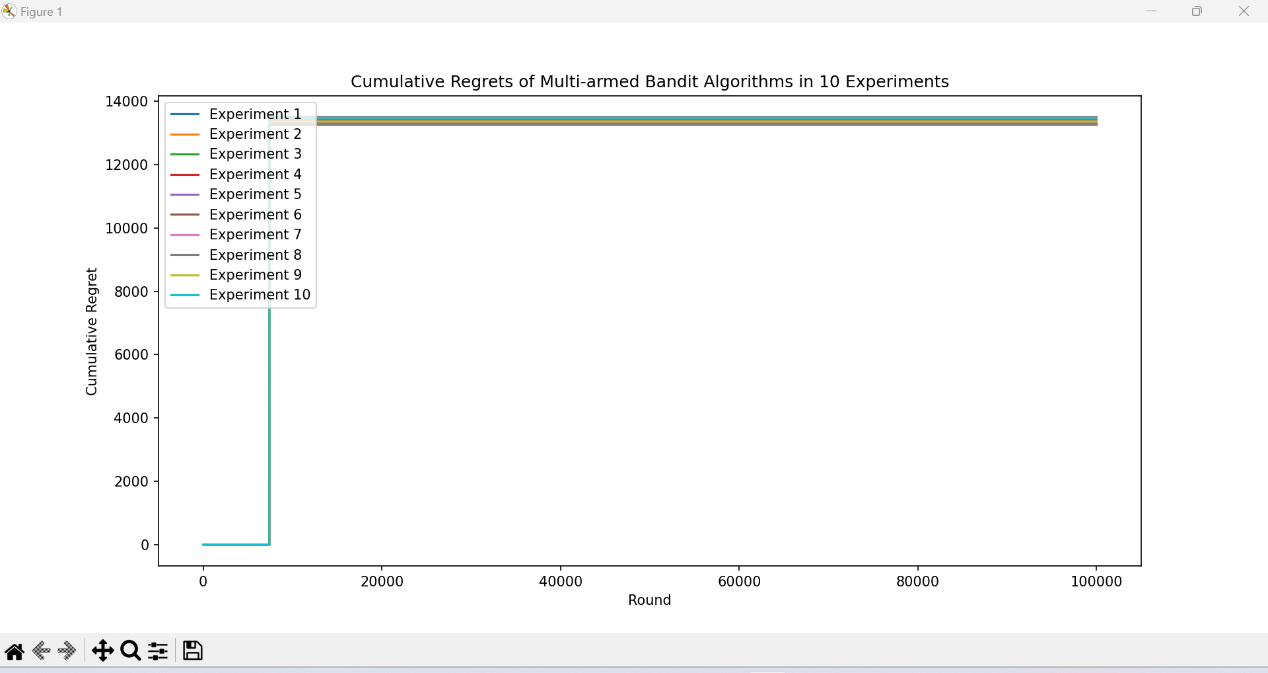
Figure 1. Cumulative Regret of ETC Algorithm in 10 Experiments (Picture credit: Original).

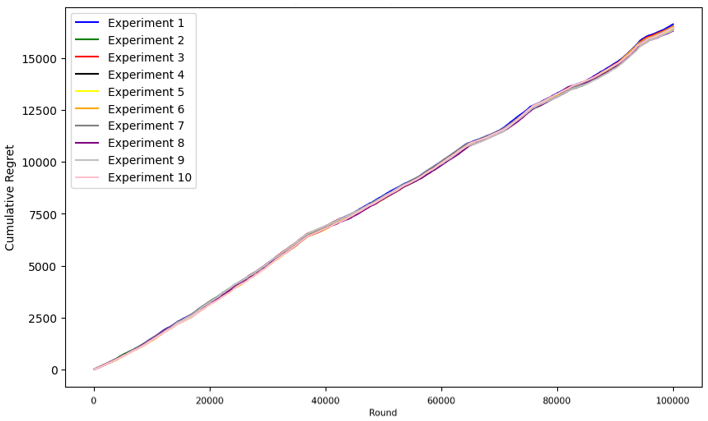
Figure 2. Cumulative Regret of UCB Algorithm in 10 Experiments (Picture credit: Original).

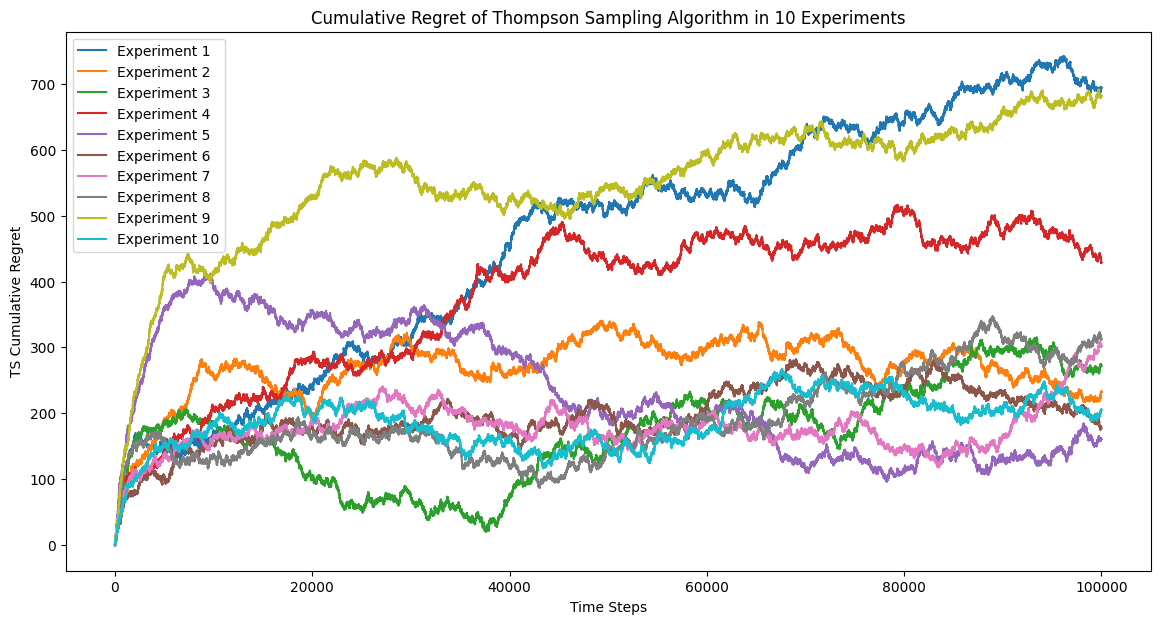
Figure 3. Cumulative Regret of TS Algorithm in 10 Experiments (Picture credit: Original).

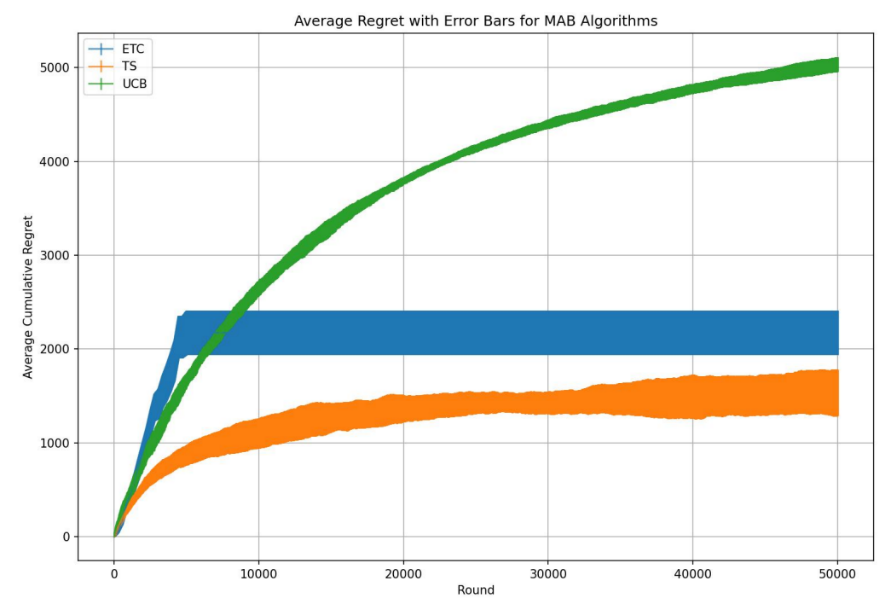
Figure 4. Average Regret with Error Bars for MAB Algorithms (Picture credit: Original).

It seems like ETC and TS algorithm has the most variation while UCB algorithm seems to be more stable.

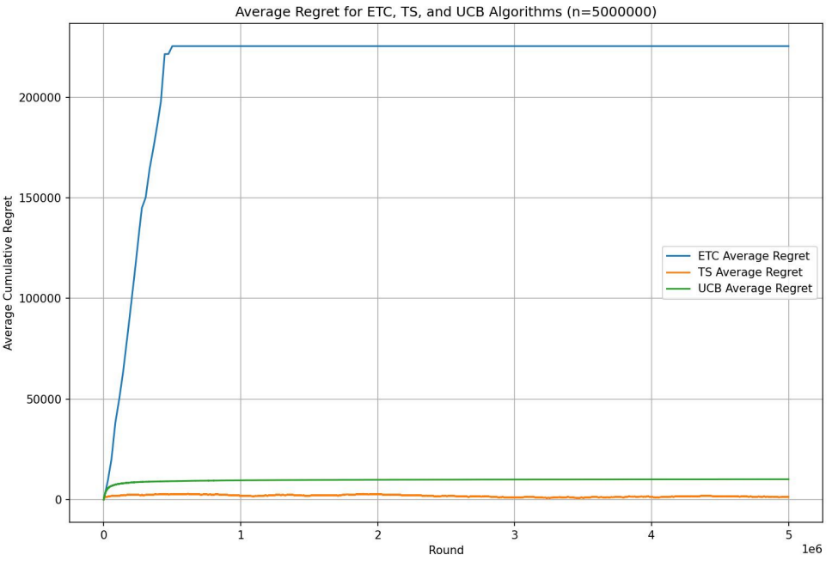
Figure 5. Average Regret for ETC, TS, and UCB Algorithms (n=5000000) (Picture credit: Original).

As is depicted in the Figure 5, the ETC algorithm exhibits the highest cumulative regret, significantly surpassing the other two algorithms. On the other hand, the performance of the remaining algorithms is relatively comparable. The Thompson Sampling algorithm ranks first, followed by the UCB algorithm. This implies that optimizing algorithm parameters and selecting the appropriate algorithm can greatly enhance the overall outcomes.

Through intuitive analysis of average regret induced by the three algorithms, it becomes apparent that for music recommendation systems, both TS and UCB algorithms are suitable choices, while the ETC algorithm may introduce significant judgment errors, thereby impacting user experience. As for the choice between TS and UCB algorithms, it largely depends on factors such as the number of users, the fine-tuning of parameters and algorithmic optimization.

This observation underscores the importance of algorithm selection in optimizing user satisfaction and engagement in music recommendation systems. While TS and UCB algorithms exhibit robust performance, careful consideration of specific contextual factors and algorithmic nuances is essential in determining the most effective approach for a given platform or user base.

4. Challenges Encountered and Future Prospect

In the context of music recommendation systems, the choice of delta parameter in UCB Algorithm plays a crucial role in balancing exploration and exploitation to enhance user satisfaction. Larger delta values tend to slow down convergence rates as the algorithm prioritizes exploring less-known music genres over exploiting those with higher estimated rewards. Consequently, this delays the system's ability to discover the true optimal music genre, as it spends more time gathering information through exploration. Conversely, smaller delta values lead to faster convergence rates, as the algorithm focuses more on exploiting the known music genres with higher estimated rewards. This enables the system to approach the true optimal music genre more swiftly, resulting in quicker and more accurate recommendations for users.

However, it's essential to consider the limitations of the provided value of \( n \) , representing the total number of recommendation rounds. This value may not be large enough to fully capture the effects of different delta values on convergence rates. As a result, the plot generated from the given code may not offer a precise representation of the performance differences between the algorithms. To obtain more reliable results, it's advisable to increase the value of \( n\ \) to allow for a more extended exploration-exploitation trade-off and conduct additional experiments, ensuring that the music recommendation system achieves optimal performance in providing personalized and satisfying recommendations to users.

As for Thompson Sampling (TS) algorithm, it involves random sampling of parameters and updating posterior distributions, which can lead to higher computational complexity. For large-scale music libraries and extensive user bases in recommendation systems, this high computational cost can pose a challenge. Additionally, as a method based on random sampling, TS algorithm may exhibit instability in certain cases. Particularly in scenarios with sparse data or frequent variations, inherent randomness can result in uncertainty in recommendation outcomes, consequently affecting the user experience.

Although UCB and TS algorithm faces many challenges in music recommendation system, there is no denying that it plays a pivotal role in refining recommendation systems and enhancing the overall listening experience for diverse user base.

By utilizing three advanced algorithms, the potential of personalized audio experiences within music recommendation systems is explored. These algorithms offer promising avenues for enhancing user satisfaction and addressing algorithmic bias, thereby empowering Spotify teams to better serve diverse audiences and creators. Spotify aims to provide users with enriched and diverse music recommendations while ensuring fairness and inclusivity in the platform's recommendation processes. This approach not only enhances user satisfaction but also promotes diversity and representation within the music industry.

5. Conclusion

In a detailed comparison of the Explore-Then-Commit, Upper Confidence Bound, and Thompson Sampling algorithms using the same user dataset in the music recommendation arena, this study seeks to identify the algorithm most effective in resolving the user-artist matching challenge, thereby enhancing recommendation accuracy. The study reveals that the ETC algorithm incurs significantly higher regret values compared to UCB and TS. This can be attributed to ETC's methodology of fixed exploration rounds for each strategy, followed by complete exploitation of the seemingly optimal strategy. This approach often leads to the premature dismissal of potentially superior choices, resulting in notable inaccuracies. The rigidity in exploration phase settings may also cause an under-exploration of the full potential of various options, thus overlooking high-reward opportunities. Additionally, the algorithm’s inflexibility in transitioning between exploration and exploitation, based on a predetermined round count, can impede adaptability to environmental shifts, such as changes in user preferences or updates to the music library, leading to performance declines. In contrast, both UCB and TS demonstrate enhanced performance in music recommendation, showing negligible differences between them. Their success is attributed to a more dynamic equilibrium between exploration and exploitation. These algorithms, by continuously adjusting the exploration-exploitation balance and estimating the confidence or probability of different choices, are better equipped to modify strategies in response to real-time feedback and environmental alterations. The real-time updates of parameters and posterior distributions enable these algorithms to adapt more effectively to shifts in user preferences and changes in the music content. Consequently, these advantages generally translate to improved functionality in music recommendation systems, resulting in more tailored and satisfying user experiences.