1. Introduction

At present, shortcomings still exist in the automatic course selection and course scheduling system despite its wide application. Mistakes such as time conflicts can occur frequently, which is not convenient for students' course management. In addition, due to a lack of intelligence and science, the staff needs to make repeated adjustments when scheduling conflicts occur [1]. Intelligent algorithms such as the genetic algorithm (GA) [2-3] and ant colony algorithm [4] take a long time and achieve low results.

Under this circumstance, the greedy algorithm [5] is used in this paper in order to find the optimal solution to course selection and course scheduling problems. In this paper, the author first studies the properties of greedy algorithms and then applies them to concrete examples. Finally, the global optimal solution is obtained by several local optimal solutions.

The research method of this paper focuses on specific case studies. This article establishes a one-to-one match between all students in the same class, the teacher in that class, and the classroom they need. Everyone's common free time can be found with the help of greedy algorithms, and the time is used to schedule the necessary lessons.

This article can make it easier for educators to manage students' classroom schedules, offer better time plans, and improve the living arrangements of each student and teacher. In addition, it can better explain the application of greedy algorithms in daily life, provide references including examples, broaden the perspective of researchers, and help researchers solve more potential time allocation problems.

2. The basic concept and application scope of the greedy algorithm

The idea of greedy algorithms is to start from the initial solution of the problem and go step by step according to certain optimization measures. Each step is made to ensure that the local optimal solution can be obtained. Only one data is considered at each step, and its selection should meet the conditions of local optimization. If the next data is no longer a viable solution together with the partial optimal solution, no more data is added to the part of the solution until all data enumerations are completed.

Greedy methods do not seek optimal solutions or require backtracking, they only seek a more satisfactory solution. Although the greedy algorithm cannot obtain the overall optimal solution for all problems, it is the most straightforward algorithm design technique for a wide range of optimization problems. It always breaks down the whole problem-solving process into small steps, determines the processing order according to its difficulty, makes the local optimal choice at present, and gradually approaches the given goal to obtain satisfactory processing results as soon as possible [6].

Greedy algorithms have several key points in the actual solution process: the first is to set the initial conditions. Usually, the initial conditions are generated based on the problem to be solved, but to the extent that the conditions allow, it is possible to combine the best starting conditions with a method to solve the locally optimal solution later. The second is how to solve the local optimization problem. The optimization problem is usually solved by putting forward the optimization function, and the quality of the optimization function directly determines the quality of the whole greedy algorithm. This is the most critical part of the greedy algorithm. The third point is to establish final conditions. The so-called final condition includes two points: one is the end condition of the overall greedy algorithm, which should be determined according to the accuracy requirements of the problem; the other is the constraint on the optimal choice of each local stage, which determines whether the optimization function has been optimized.

3. The role of greedy algorithms in the course selection and scheduling system

3.1. The role of greedy algorithms in the course selection system

During the course selection process, in which a small number of subjects are involved and only the students who choose the course are included, we just need to handle the amount of concurrency that the system can handle using normal methods and make sure that students choose the corresponding courses they want in order. The greedy algorithm is used to sort students nearby and monitor the list of students in each course to ensure that there are no anomalies in the course selection process where the latter students are ranked ahead of the former students or the number of students exceeds the capacity of the course.

It should be noted that the greedy algorithm can only sort students according to the local optimal solution, and it cannot guarantee that students are completely satisfied with the previous course arrangement and the courses they continue to choose. However, the above problems can be solved by students' simple thinking and choice, so it can be seen that this shortcoming of greedy algorithms can also become the advantage of increasing students' freedom of course selection, which is the double-sided advantage and disadvantage of greedy algorithms.

The steps for students to select a course mainly include the login interface, confirming the schedule of required courses, selecting optional courses that can be selected, reconfirming the schedule, etc., until all courses have been selected. This process involves frequent loops, in each of which the greedy algorithm can help students determine whether the course they have chosen is an elective, whether it conflicts with other electives or required courses, or whether it meets preset online or offline course requirements, as shown in Figure 1.

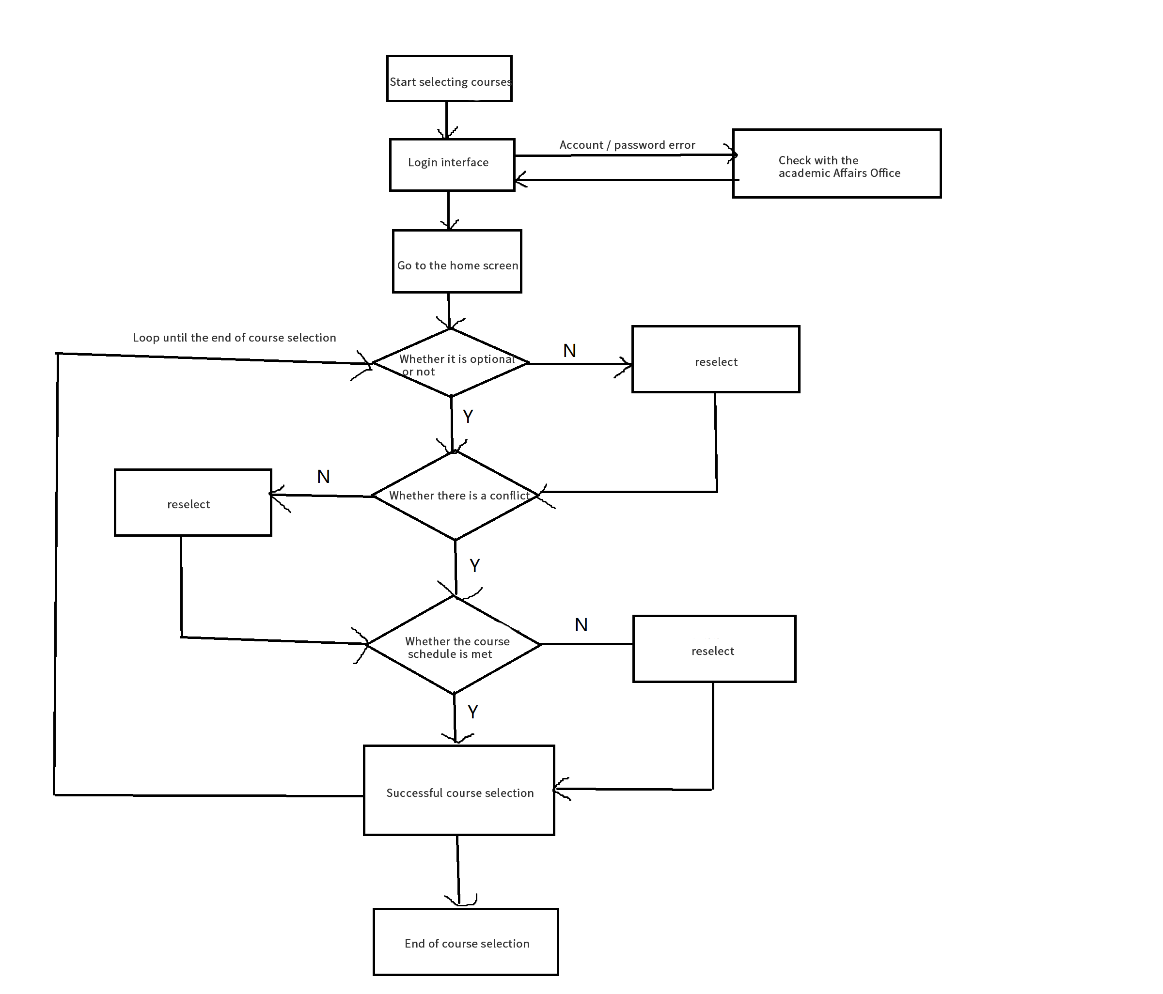
Figure 1. Application process of greedy algorithm in course selection.

3.2. The role of greedy algorithms in the course scheduling system

The essence of the course scheduling process is the optimization process of five basic elements: teacher, classroom, class, course, and time [7]. The main task of course scheduling is to assign teachers to the classes of the whole school according to the teaching plan for this semester, reasonably arrange class time and classrooms, and ensure that there is no conflict in course scheduling. The ultimate goal of course scheduling is to make full use of the school's teaching resources and obtain the best teaching effect under the premise of satisfying all kinds of soft and hard constraints.

The hard constraint conditions refer to the conditions that must be met in the course scheduling. If they are not met, something impossible will happen in the concept of time and space between teachers, students, and the classroom, resulting in conflicts in class [8]. A good class schedule should be able to meet the administrative requirements of the school, meet the basic requirements of all participants, and schedule most classes as much as possible to the satisfaction of teachers and students. In view of the above, in order to arrange a satisfactory schedule, the following basic principles must be observed in the course scheduling: students in a class can only arrange one course at a time; teachers can only schedule one course at a time; only one course can be arranged in a classroom at a time, and the classroom type must meet the requirements of that course; the classroom capacity for each course must be greater than the total number of students enrolled in the course; the total number of courses scheduled at one time cannot be greater than the total number of available classrooms; one cannot schedule each class twice; each course must meet the required number of credit hours.

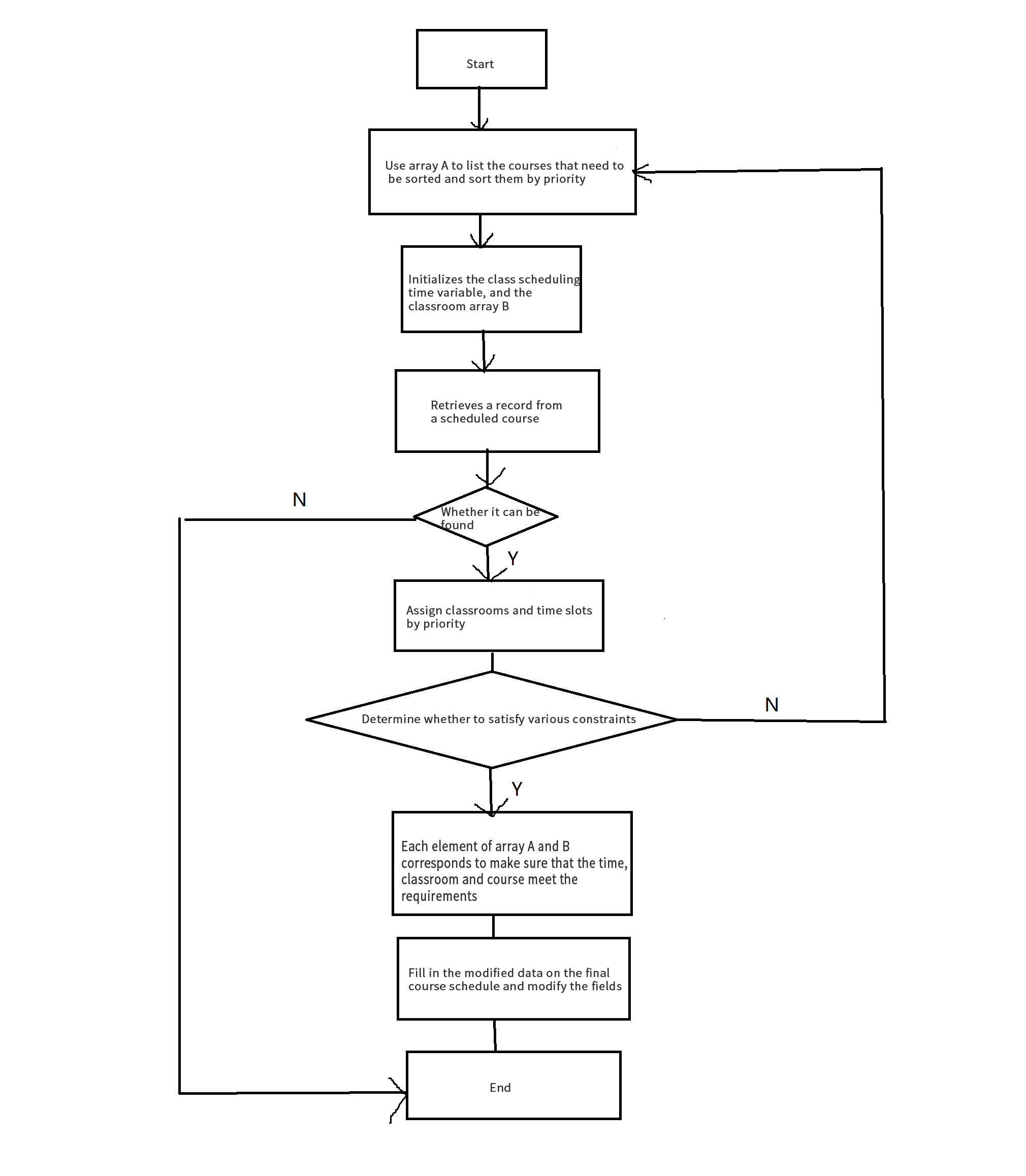
Figure 2. The application process of greedy algorithm in the course scheduling process.

At the same time, in order to make the course arrangement more reasonable and humane, the following factors should also be considered: the class time of each course in a week should be distributed as reasonably as possible. It should be arranged according to the requirements and characteristics of the course, for instance, basic courses, theoretical courses, and professional courses should be arranged in the morning as far as possible, while elective courses should be arranged in the afternoon as far as possible. For two consecutive courses, the classrooms should be switched as little as possible, or they should be arranged close to each other. Different lectures for the same course should be arranged in the same classroom as much as possible, and they should be evenly spread out over different days of the week so that teachers have enough time to prepare the course and students have enough time to review and digest. Given that most teachers expect to teach different classes consecutively, the same teacher should be scheduled as many different classes as possible each day. The schedule of compulsory courses should be made as balanced as possible; the objective requirements of each course should be met as far as possible; the special class time requirements of individual teachers (e.g. external teachers) should be considered. For example, physical education classes are not scheduled in the morning or on holidays. Classroom functions should meet classroom requirements (language room, multimedia room, general classroom, laboratory, etc.).

In the course scheduling process of greedy algorithms, the following principles should be considered, for example, the course priority is high, and the number of available courses must meet the requirements of the course, as shown in Figure 2.

4. Detailed algorithm and process

The system adopts the priority greedy algorithm. The course scheduling process based on the priority greedy algorithm is based on the manual course scheduling process, taking the course to be scheduled as the unit, selecting the appropriate time around the free time of each teacher and classroom, and selecting the optimal resources in the time used for course scheduling. After the schedule of each class is set, the schedule of the teacher and the classroom is set accordingly.

When there is no shortage of teaching resources, the greedy algorithm based on priority can produce a relatively reasonable class schedule. The greedy algorithm always breaks down the whole big problem-solving process into a relatively small step, determines its processing order according to the designed problem-solving principle, makes the current local optimal choice, and gradually approaches the given goal to obtain satisfactory processing results as soon as possible. Although greedy algorithms can not obtain global optimal solutions for all problems, they can produce global optimal solutions for many problems, such as the container loading problem, knapsack problem, topological sorting problem, binary coverage problem, shortest path problem, and minimum cost spanning tree problem.

In some cases, even if the greedy algorithm cannot get the global optimal solution, its final result is a good approximation of the optimal solution. The specific execution process of the algorithm is described as follows: initialize all the classes and classrooms to be scheduled, calculate the priority of each class, and rank the classes according to the priority. The main content of the general class scheduling problem consists of two parts, one is the allocation of teachers' class time, and the other is the allocation of classrooms and teaching equipment, which is the so-called resource allocation problem. Considering that teachers' class time each semester is basically consistent and has strong stability, the algorithm does not take teachers as the basic factor in the course scheduling but uses teachers who directly designate classes when entering the course scheduling. At the same time, in order to prevent teachers from conflicts in the course of course scheduling, conflict detection should be carried out in the automatic course scheduling module and manual course scheduling module.

5. Conclusion

In this paper, the course selection and scheduling system of college students is deeply studied, and the greedy algorithm is adopted to meet this demand. First, the system strives to extend from the local optimal solution to the global optimal solution by continuous use of greedy algorithms and the limited idea of mathematics. This enables students to better use the course selection system and freely choose courses when they are legal, compliant, and in line with the schedule.

Second, it also allows educators responsible for scheduling classes to reduce the burden of heavy human scheduling. Because course scheduling is a nonlinear multi-objective optimization problem, the designed algorithm should be simple to operate and set fewer parameters [9]. Greedy algorithms can help streamline operational steps, and based on greedy algorithms, people can quickly identify conflicts in their class schedules and ensure that everyone's time is arranged at minimal cost.

In addition, the greedy algorithm also involves the arrangement of teachers' free time, the arrangement of free classrooms, and the coordination of the flow of personnel in each teaching building to prevent crowding and stampedes.

Greedy algorithms play an important role in the course scheduling system, and efforts need to be made in future studies to further improve the algorithm to eliminate more human labor.