1 Introduction

The Cops and Robbers game is a famous game modeling pursuit and evasion in graph theory. It is introduced by Nowakowski and Winkler [1]. The game needs two players, called cop and robber, to play a game on a graph G according to the following rules: First the cop then the robber occupies some vertex of G. After that, they move alternately along the edges of G. The cop wins if he succeeds in putting himself on top of the robber, otherwise the robber wins.

In this game, the winning strategies for both the cop and the robber depend on the structure of the graph. If the graph is connected, which means the cop is able to reach the robber’s vertex, the winning strategy of the cop is to chase the robber along a path in a way that it can keep or decrease the distance between them in each step. If the graph is acyclic (no cycles), the cop can employ a more efficient strategy by moving along the linear path between them. The robber can have a winning strategy when the graph includes cycles. The strategy is to move along the cycle to keep their distance the same at every step.

The Cops and Robbers game includes multiple types of variants. The variant might change the number of cops and robbers [2], the ways players move [3, 4], or the ways they detect each other [5]. As the graph and rules change, the winning strategy also changes.

The reason people study these variants is not only for studying and solving graph theory problems, these variants and their winning strategies can play a big role in the model and algorithm of machine learning. Pursuit-evasion games have numerous applications including artificial intelligence, robot motion planning, database theory, distributed computing, and algorithmic theory [6]. However, the cops and robbers game is designed to be played on a graph, so many papers about the variants of the cops and robbers game only focused on studying mathematic characteristics and algorithms. The numerous numbers of articles about applications only introduced the pursuit-evasion game. It’s hard to find an article introducing cops and robbers game for a model of artificial intelligence or robot motion planning. So the purpose of this paper is to focus on finding the specific relations between pursuit-evasion game applications and variants of the cops and robbers game.

2 Method

To find the specific applications of each variant and sort them, the pursuit-evasion game and the variant should be the same or similar to make sure the specific application is suitable for this variant. In order to prove the pursuit-evasion game used the same algorithm as the variant, both their game rules and winning strategies will be taken out for comparison. If they follow the same rules and use the same winning strategy, then this study about pursuit-evasion game is a possible application of this variant.

This paper first finds some different types of variants of the Cops and Robbers game, classifies them according to their game rules. Then looks for articles related to pursuit-evasion games and machine learning, and studies the models used in them, finding the game rules, winning strategies, and how they work in this application. The rules and winning strategies are used to compare and find related variants.

To cover more types of variants, this paper classifies different variants and tries to discuss them together. For example, adding the number of cops to 3 or 4 is one way of changing the number of cops. The application might be more specific, such as only using 3 cops as a model. In this case, this application might refer to the variant that changed the number of cops, but the paper will describe it more specifically because the winning strategies and algorithms might change based on the numbers.

Some articles only describe the game rules but not the winning strategies, in this case, the articles might show different strategies or algorithms. Also, the cops and robbers game is a pursuit-evasion game on a graph, so this paper can only sort all relations between the variant and application, it can’t prove a variant can be used in the same way for an application.

3 Types of Variants

3.1 Number of Cops

The number of cops is a simple variant of the game. In the same graph, the number of cops affects the winning strategy of the game. For example, if there is only one cop in a pentagon (Figure 1), the cop will never catch the robber while the robber goes around the pentagon. But if there are two policemen in the picture, they can surround the robber directly in a line, then narrow down the area, and finally catch him [7]. In the former condition, the robber has a winning strategy. In the latter condition, the cop has a winning strategy. Therefore, the number of cops will have different effects on a given graph. The number of cops is a special and popular problem in cops and robbers games. People often study this problem under different graphs or game conditions.

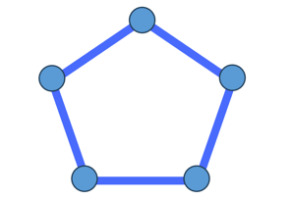
Figure 1. Graph of pentagon

Some people have studied the minimum number of cops needed in different graphs for the cop to have a winning strategy to catch the robbers. One example is the study of Fromme, which says that in a planar graph, a maximum of 3 cops is enough for the cop player to win [2]. Other multiple studies focused on the minimum number of cops in other types of graphs. Lu proves that for general connected graphs, the upper bound of the cop number is \( c(G)≤O(\frac{n}{2^{(1-O(1))}\sqrt[]{log_{2}n}}) \) [8].

One application of this type of problem is an article that introduces pursuit-evasion games for intelligent agents in the Unity 3D environment [9]. In this game, the player is an evader on the map, while the remaining 4 pursuers are controlled by the game’s intelligent agent. These 4 pursuers controlled by the game use a game variant of 4 cops. However, the rules of this Unity game are more complex, with settings for visibility and information sharing. Therefore, the specific model and algorithm must be different from the four simple police game variants.

Figure 2. Game environment design [9]

3.2 Speed of Cop and Robber

Speed and acceleration are another type that differs from the number of cops and robbers because they focus on the movement of two players, they determine the number of vertices the player can move in each step. Usually, speed is the parameter that determines the average number of vertices a cop or robber takes per step. A difference in speed between the cop and the robber can create changes between the cop-win graph (the graph that cops must win if they follow the winning strategy) and the robber win graph. For example, in the graph in Figure 1, the robber will win if both players can only move one vertex in each step. If the speed of the cop changes to 2 vertices, then it will run faster and be able to catch the robber. In the most common cops and robbers game, both sides have a velocity of 1 and an acceleration of 0. If the acceleration is added as a parameter to the game and is not zero, then in different turns, the players can take different numbers of moves.

A simple example of this variant is Mehrabian’s study on faster robbers, which examines the upper limit on the number of cops if the robber had faster speed than the cop.

For the variant that studied both variables, an article talked about speed restrictions and provided some findings [4]. It first constructs a situation of infinite speed and studies the winning strategy under that condition. Then it searches for situations in which the cops will have a winning strategy. This article mentioned speed-(s,s), which is defined as both the cops and the robbers are allowed to move along paths of length at most s on their respective turns. In the simplest cop and robber condition, it can be represented as speed-(1, 1). In this variant, the speed and acceleration of cops and robbers will change randomly.

In an article about the pursuit evasion game in the presence of obstacles, the learning method of chasing and escaping two robots in the case of obstacle avoidance is studied [10]. The article states that in order to be applied to real-world systems, the players in the game are mobile robots whose kinematics need to meet the non-holonomic constraints, velocity constraints and acceleration constraints. Therefore, if a variant of cops and robbers is chosen to simulate the motion of real objects, it is inevitable to include the speed and acceleration of police and robbers into the parameters of this variant.

3.3 Visibility of Cop and Robber

The visibility of the cop is also a variant direction that has been studied. In most variants of cops and robbers, visibility means the cop will get the location information of the robber only when the robber is a few steps away from him, which means the cop will get the information of the robber depending on the distance between them. For example, zero visibility means the cop is chasing an invisible robber, and one visibility means that only when two players are adjacent can the cop get location information about the robber. The winning strategy of cop will be affected by different states (visible or non-visible). The cop needs to predict the movement of the robber at first and change the strategy while the finding the robber.

The article by Yang introduced previous examples while taking a deeper look at the winning strategies of the one visibility cop on the tree graph [5]. This algorithm calculates an optimal cop-win strategy based on the number of cops and the construction of the graph.

In Lozano’s study of robot pursuit-evasion game, two players drive a robot with a rotating camera and a moving one [11]. In this game, players need to calculate their position and viewing angle to get visibility. While this is also related to visibility, most studies of the cops and robbers game do not look at this variant. In other words, although the visibility of police and robbers is an applied area, the current cops and robbers studies and pursuit-evasion game application studies define the way of obtaining visibility differently. In addition, researches on variant of visibility are often limited by the type of the graphs, which makes it difficult to use current research results to support practical applications.

4 Conclusion

After conducting research and summarizing the findings, it was discovered that it is difficult to directly connect the cops and robbers game with the application scenarios that introduce the pursuit-evasion game as a model. Because the cops and robbers game is a game built on a graph, its analysis of deduced using mathematical theories in graph theory. Compared to the real-world environment, a graph can oversimplify a lot of problems. In the graph, the players can only stay on the vertices and move along the edges. However, in some practical cases, the object should be able to move randomly within an area, using a graph to represent this area will simplify it and might lose accuracy. Also, some graphs might be special and worth studying in graph theory, but they are difficult to represent in practical cases.

The problem does not only appear when simplifying the reality area into a graphical situation. Many studies of the variants are not aimed at studying the winning strategy, but rather the number of police officers, the fewest paths, and the less time in different situations, which makes it difficult for some studies on variants to find relevant applications. In many machine learning models based on the pursuit-evasion game, the purpose of using pursuit-evasion game as a model is to use the model's winning strategy or algorithm to calculate the distance relationship between objects. This makes it difficult to find applications related to other studies, such as minimum police numbers.

Another point is that many applications have more complex rules than game variants, and there will always be differences between the rules, but each of these differences may affect the algorithm of winning strategy, which makes it difficult to find a high degree of similarity between the research results of variant and research application. Among the previously mentioned applications, Şahin's 3D game uses rules that include multiple police numbers and visibility at the same time [9]. In order to achieve the purpose of real-world applications, multiple functions need to be played together, but for cops and robbers games, an algorithm that calculates problem A and problem B at the same time is sometimes not directly equal to the sum of their strategies. However, the research direction on the mathematical graphs is inevitably different from the research direction of machine learning algorithms. As a result, it is difficult for current research results of cops and robbers game to be directly applicable to the developed applications.

One of the more unique applications is the game agent, which is a game that uses algorithms to manipulate characters. Because games on electronic devices can be designed based on random game rules and have a low requirement for mobility, the impact of the problem just mentioned can be weakened artificially. It is the most likely application that is most similar to the research direction of cops and robbers in each application scenario.

Overall, for a number of reasons, it is difficult to find a directly related application for current cops and robbers research. Among the many applications, the game agent is an application with a higher relation to cops and robbers research. In the future, if the algorithms and strategies of the cops and robbers model are expected to be used for application, an algorithm that can adapt to a variety of situations may be a future research direction. In addition, with the development of machine learning, there have been studies about using machine learning to simulate and study the variant's winning strategy [12]. This method might be a way to help solve the problem that variant research is based on graphs and mathematical theories, which results in too many preconditions and is inconvenient for applications.