1. Introduction

The use of harmonies in musical compositions has held a timeless fascination. Consider Claude Debussy, the celebrated French composer known for his nuanced use of harmony and texture; his compositions have captivated musicians, scholars, and the public for generations [1]. Interesting use of chords imbues compositions with colors, emotions, and significance, to the extent that it is sometimes possible to identify the composer based on the stylistic chord progressions used in the composition [2].

Computational models of chord progressions (CP) have garnered increased attention in the past few decades for a range of applications, including music generation, human-machine co-performance, and compositional tools. For instance, Morris et al. employed Hidden Markov Models (HMM) to harmonize melodies with user-specified parameters [3], while Chuan and Chew utilized Markov chains to generate harmonization that emulates certain styles [4]. Choi et al. trained Long Short-Term Memory (LSTM) networks on sequences of jazz chord progression texts for music generation [5]. Carsault et al. trained both Multiple-Layer Perceptron (MLP) and LSTM structures for creating stylistically coherent CPs, integrated into the DYCI2 system for human-machine co-improvisation [6]. ChordRipple leveraged Word2vec to embed CPs and suggest contextually relevant and surprising chords to composers, resulting in more adventurous and compelling compositions [7]. More recently, the use of transformer architectures in modeling CPs has gained increasing attention [8]. Transformers are known for their superior ability to model sophisticated long-term dependencies. Li et al. trained a transformer-based model to predict CPs with given melodies [9], while Chen et al. explored expressive coloring and voicing of jazz CPs using Multi-Head Self-Attention (MHSA) [10]. Furthermore, Dalmazzo et al. provided a detailed investigation of the tokenization and encoding methods for transformer networks on a large chord corpus [11].

Modeling diverse CPs for accompaniment generation and human-machine co-creation is interesting and useful; however, less attention has been devoted to modeling musicians’ stylistic disparities and enhancing the generation of specific interesting chord progressions. ChordSequenceFactory [12], for instance, employs chord transition probabilities to model CPs, enabling both CP generation from scratch and rearrangements using stylistic CPs from musical pieces. Nonetheless, enhancing the generation of specific CPs necessitates meticulous manipulation of the matrix generations, and this approach may not generalize well to long contexts or large chord vocabularies. Such endeavors hold promise for enriching musical understanding and creativity. For example, examining how different musicians select chords within the same contexts provides insights into their unique habits and mindsets. Moreover, composers and improvisers often seek a broad array of harmonic choices to unleash their expressive potential, yet developing this intuition takes time and practice. As Ref. [7] reveals, novice composers may feel uncertain about the effect of novel CPs and their integration into their compositions. A possible solution lies in learning the CPs step by step, focusing on particular progressions of interest. By playing these CPs across various keys and contexts, musicians can build up intuition and become more acquainted not only with their distinct sounds but also with the techniques for quick reproduction, such as memorizing chord notes and chord relations, keyboard positions, and hand position changes.

Therefore, this study aims to develop a customizable model to help users learn specific stylistic CPs of interest. The study first trains a foundation model using a nano Generative Pre-trained Transformers (https://github.com/karpathy/nanoGPT) on the Choco chord corpus [13], then proposes three fine-tuning strategies to enhance the generation of the interested CPs. Section 2 provides detailed explanations of the data, training, and strategies, while Section 3 evaluates the models’ performance using existing and new metrics, including an analysis of a text-based user interface. The study’s limitations and future directions are covered in Section 4, and Section 5 summarizes the study’s findings. This paper makes two main contributions: the design and evaluation of three fine-tuning strategies to influence the foundation model’s behavior, resulting in improved generation of musically coherent CPs; and the proposal of a new mode of generation that can illuminate chord novelty assessment and offer a creative approach to learning and sharing chord styles.

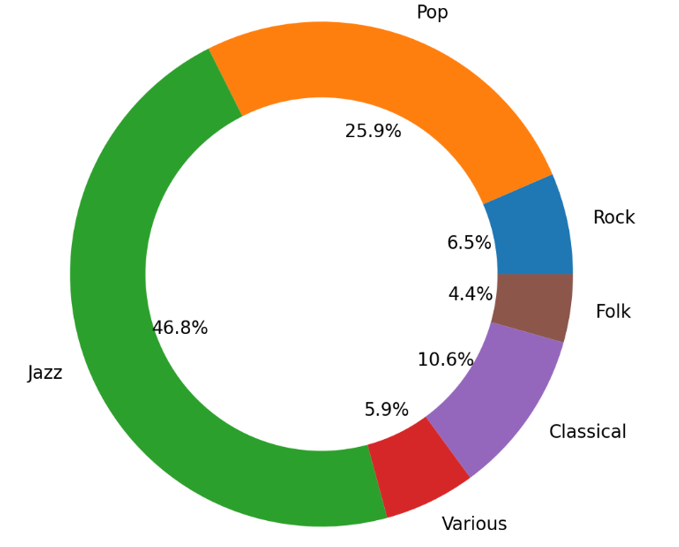
Figure 1. Music genre distribution (Photo/Picture credit: Original).

2. Data and method

2.1. Choco dataset

The model is trained on sequences of Harte-style chord notations obtained from the Choco Dataset [13], which encompasses a variety of musical styles, including jazz, pop, and classical. Fig. 1 provides an approximate breakdown of the style distribution within the dataset, indicating jazz and pop as the predominant styles. The dataset comprises chord progressions extracted from a total of 20,086 musical pieces, amounting to 1,456,821 individual chords. To augment the dataset, the CPs are transposed to 18 equivalent keys around the circle of fifths. It is important to note that this transposition process does not consider converting notations to enharmonic equivalents based on music theory conventions. For instance, in E major, the pitch D sharp is conventionally notated as D# rather than Eb. However, during transposition, all D# are converted to Eb.

Although additional musical features such as chord duration and time signature can influence the choice of CPs, the training data used in this study consists of symbolic chord notation only. Such an approach has certain limitations as pointed out by [14]; however, the focus of this study lies in exploring the creative potential of fine-tuning chord models. Future research endeavors may consider enhancing model performance and musical expressiveness by incorporating encodings of more musical features.

2.2. Fine-tuning dataset

In addition to the Choco Dataset, the model undergoes further fine-tuning using chord progressions extracted from a single musical composition of interest. For illustrative purposes, this study utilizes the chord progressions from a game soundtrack (WitchSpring2, “parting and gathering”). The list of chord symbols are: F:maj7, E:min7, D:min7, C:maj, Bb:9(#11), F:maj7, E:min7, A:min, F#:hdim7, D:hdim7/b3, E:min7, A:min, F:maj, E:min7, A:7, D:min7, and C#:min7. The fine-tuning data is augmented using the following three strategies:

• Raw sequence: The complete CP is transposed to 18 equivalent keys, serving as the baseline approach.

• Increasing context: Starting from the given CPs of interest, new CPs are created with progressively more chord symbols from the CPs preceding the target progressions (A, BA, CBA…). These sequences are then transposed to 18 equivalent keys.

• Generated context: Leveraging another chord model trained on sequences of reversed chord symbols, previous chord symbols are generated from the given CPs of interest. The generated symbols are combined with the target CPs and transposed to 18 equivalent keys.

While Strategy 1 provides a baseline with all subsets of the progressions having equal frequency of occurrences, in practice, musicians are often more interested in certain unconventional subsets. To address this, the study proposes to augment the frequency of preferred subsets in the dataset used for fine-tuning, increasing the likelihood of the model predicting these CPs. The CP of interest in the listed chords is F#:hdim7 -> D:hdim7/b3, because the progression creates an unusual color due to the use of non-diatonic pitches in both chords as well as the stylistic sound of consecutive half-diminished seventh chords. Another famous use of this progression occurs in the opening piano part of Sergei Rachmaninoff’s Piano Concerto No.2 mvt. 2. The study hypothesizes that both Strategy 1 and 2 may perform poorly when faced with a more diverse chord context, for example, unseen combinations of CPs. To tackle this challenge, Strategy 3 is introduced. This strategy involves training another model to generate a musically appropriate and more diverse context preceding the target chord progression. Context generation is achieved using recursive sampling paths with specified depths.

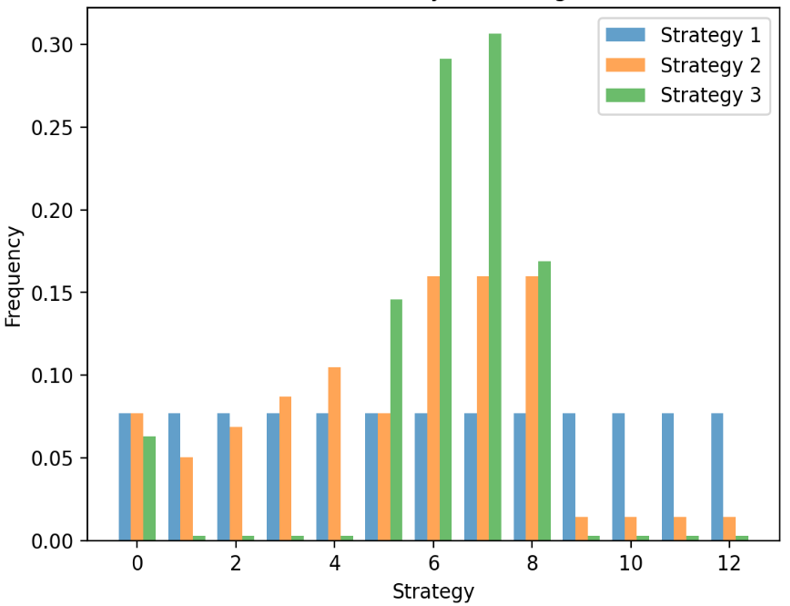
Figure 2. 2-gram distribution per strategy (Photo/Picture credit: Original).

Fig. 2 reveals the 2-gram chord distribution of the three generated datasets, represented as percentages. An N-gram chord distribution analyzes occurrences of potential subsets of size n within CPs. Notably, the distribution considers all n-gram chord progressions in equivalent alternative keys, prioritizing the relationship between chords. This metric is valuable as the relationship between adjacent chords often holds greater significance in music composition, performance, and listening. While Strategy 1 exhibits uniformly distributed 2-gram CPs, both Strategy 2 and 3 demonstrate an increase in percentage from the 7th to the 9th 2-gram CPs, encompassing the CP of interest.

2.3. Tokenization

The study predominantly adopts the tokenization method proposed by [11]. A Harte chord symbol is decomposed into a tuple of tokens, consisting of the chord root (e.g., Bb, A), quality (e.g., min, maj), added notes, and bass. For example, the symbol Bb:maj(11, 13)/5 will be parsed into ‘Bb’, ‘maj’, ‘add’, ‘11’, 13’, ‘/’, ‘5’. Each chord is separated by a ‘.’ token, while a [eos] token is inserted between individual sequences of CPs to denote the start of a new piece. This tokenization process results in a final token vocabulary size of 75, with a total of 82,107,585 tokens obtained.

2.4. Model

The study initiates by training a nano GPT foundation model on the dataset. The model has a fixed block size of 256, with 384 embeddings, 6 layers, and 6 attention heads. Training extends over 2000 iterations (~8 epochs), using a batch size of 64 * 20 (utilizing gradient accumulation) and a 1e-4 learning rate, which cosine decays down to 1e-5. Similar to [11]’s observation, no signs of overfitting were observed during training, suggesting that the model can be bigger and trained with more epochs. Subsequently, all trainable units of the model undergo fine-tuning for 50 epochs using a learning rate of 3e-5 on datasets generated by the three strategies outlined earlier. No further modification of the model structure occurs during fine-tuning. The training and validation loss, together with the HITS@k metric, are recorded for both the base model and fine-tuned models. Additionally, the study utilizes the n-gram chord distribution as a metric for evaluating fine-tuned models. HITS@k metric is calculated by Eq. (1), where I is a function that returns 1 if the target’s rank is smaller than k and 0 otherwise:

\( HITS@k =\frac{1}{n}\sum _{i=1}^{n}I(ran{k_{i}}≤k) \) (1)

The N-gram chord distribution is assessed in two modes of generation:

• Generation from scratch: The fine-tuned model generates tokens from an initial [eos] token until a predefined maximum token length.

• Joint generation: Both the foundation model and the fine-tuned model generate tokens simultaneously from an initial [eos] token. Kullback-Leibler (KL) divergence is calculated between the output distributions of the two models. If the divergence exceeds a predefined threshold, the token generated by the fine-tuned model is selected. Otherwise, the token from the foundation model is appended to the token sequences as context for next-token prediction.

The “joint generation” mode is intended to simulate how a user interacts with the system for chord suggestion. By selecting tokens based on KL divergence thresholds, the system simulates the degree to which users follow suggested chords. A higher threshold implies that only chords with a significant difference in probability distribution are selected. The foundation model in this context represents the user’s habitual chord selection given a harmonic context, while the fine-tuned model embodies a new mindset for chord selection. A significant KL divergence suggests that the fine-tuned model has learned distinct patterns or preferences compared to the foundation model, given the same harmonic context.

3. Results and Discussion

3.1. Foundation model

Table 1 reveals the training/validation loss and HITS@k metric for both the foundation model and fine-tuned models. The foundation model exhibits no sign of overfitting during training and thus can be trained with more layers/heads and more epochs. An interesting observation is the notable discrepancy between the HITS@1 and HITS@3 scores. This suggests that while the model can reasonably predict the next chord, its confidence in the prediction might be misplaced. Moreover, the training data size is considerably larger (about 5 times bigger) than the dataset used in [11]. Training a larger GPT model with more epochs can potentially capture stylistic and contextual information more accurately.

Table 1. Training Loss, Validation Loss, HITS@k

3.2. Fine-tuned models

According to Table 2, the fine-tuned models exhibit increasing training/validation loss across the three strategies. Given that the dataset generated by the first strategy contained the least variations, it is expected that the model would converge quickly to a low training and validation loss with the highest HITS@k score. Conversely, Strategy 3, with the most diverse chord context, demonstrates the worst performance across all metrics in the table. In addition, only Strategy 3 shows a tendency to overfit around 40 epochs of training. Table 3 illustrates the HITS@k metrics of the three fine-tuned models on the foundation model’s validation dataset. Each model shows a significant drop, suggesting a deviation from the original model. Notably, Strategy 3’s model consistently exhibits the lowest scores.

Table 2. Training Loss, Validation Loss, HITS@k

Table 3. HITS@k on Original Dataset.

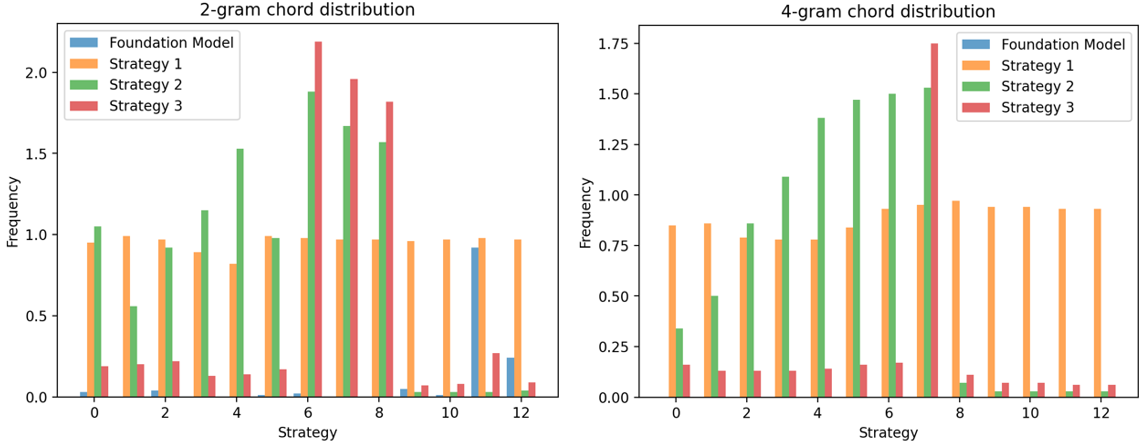
Figure 3. 2-gram and 4-gram chord distribution per strategy (Photo/Picture credit: Original).

Subsequently, this study commences with an analysis of the foundation model’s n-gram chord distribution on the CPs from the game soundtrack, followed by a comparison of the fine-tuned models’ performance in two modes of generation. For consistency, all models predict 60 tokens (approximately 20 chords) 100 times, and the occurrences of n-gram CPs are averaged per iteration. As demonstrated by Fig 3, the most frequent CP generated by the foundation model is the E:min7 -> A:7 -> D:min progression (CP 11 and 12), commonly known as the “ii-V-i” progression, a prevalent pattern found across many styles. However, the few occurrences and the absence of other chord progressions indicate a significant stylistic difference between the target CP and the foundation model’s generated CP. As seen from Fig. 3, the CPs generated by strategy 1 exhibit a mostly uniform distribution in both the 2-gram and the 4-gram chord distribution. This suggests that the model’s predictions largely adhere to the chord order observed in the original dataset. In contrast, Strategies 2 and 3 demonstrate a noticeable increase in the occurrence of 2-gram chord progression number 6, 7, and 8, encompassing the CP of interest. Due to how Strategy 2’s dataset is structured, the results for Strategy 2 reveal a progressively higher occurrence of the 2-gram and 4-gram CP. Strategy 3’s generation contains target chord progression to the greatest extent despite its poor performance in terms of loss and HITS@k metric.

For joint generation, the 2-gram chord distributions generated from three KL divergence thresholds (1, 3, 5) are recorded for comparisons (seen in Fig. 4). It is evident that the chosen level of KL divergence threshold influences all three models in producing correct 2-gram CPs. Higher levels of KL divergence thresholds decrease the likelihood of the fine-tuned model’s predictions being chosen. This can lead to the generated chords being less familiar to the fine-tuned model, further hindering its ability to produce the correct CPs. Furthermore, while the graphs illustrate an increase in the 2-gram distribution for all strategies as KL divergence decreases, only Strategy 3 consistently achieves a significantly higher frequency in the target CP compared to the other models. Since varying levels of KL divergence thresholds can generate different contexts, this indicates that Strategy 3 is the most responsive to different harmonic contexts and capable of guiding users toward the target CP.

Additionally, the difference in KL divergence can serve as a metric for chord novelty. Previous scholars have utilized metrics such as overall chord frequency in a set [7] or distance-based metrics [4] to assess chord novelty. However, an equally important aspect of chord novelty is its perceived newness and interest to individual users, which can be highly subjective due to levels of musical training [15] and aesthetic interest [16]. By fine-tuning a foundation model on two stylistically distinct sets of CPs, chord novelty can be effectively represented by the KL divergence between the two fine-tuned models during predictions. As observed in the study, the KL divergence will be small for common CPs but significantly larger if one of the models learns to respond differently when given the same chord context. This reflects not only the statistical differences between the two sets but also signs of disparities in habits and mindsets, which are indicators of relative chord novelty to individual users.

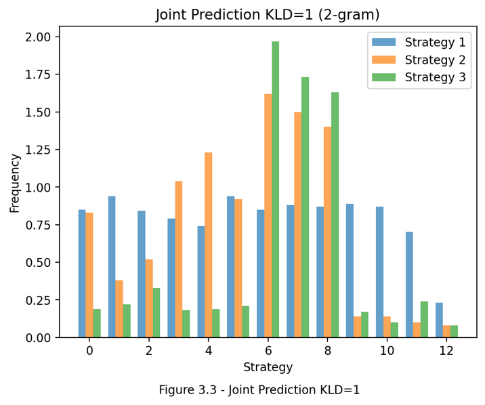
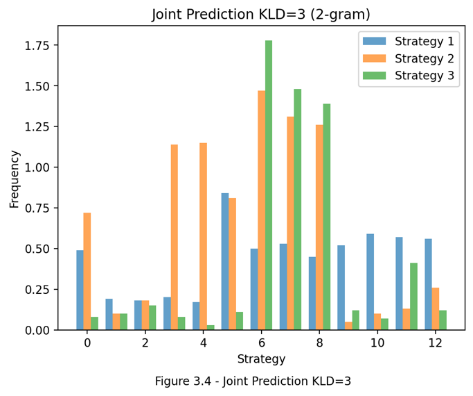
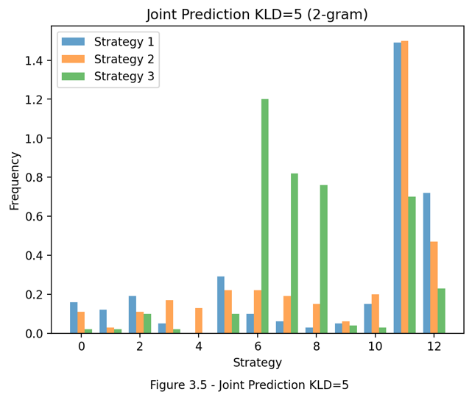
Figure 4. Joint prediction for KLD=1,3,5 (Photo/Picture credit: Original).

3.3. Usage case and analysis

A demonstration and use-case analysis are presented here, involving a text-based interactive interface with the model fine-tuned by Strategy 3. Table 4 contains example outputs, where “tok_seq” represents the tokenized user input, and “suggested chord” represents the model’s prediction along with its probability. The user interacts with the interface by entering a Harte-style chord symbol at a time, and the terminal colorizes the log to indicate the model’s confidence in its predictions.

Table 4. Example Output

The model demonstrates increased confidence in predicting the target progression when relevant combinations of chord symbols are presented. For instance, when the sequence starts with A:min and D:min (a v-i progression), establishing the key of D minor, the model accurately predicts the half-diminished chord, which should be a minor third below the preceding minor chord. This pattern holds for progressions like “A:min, D:min, E:maj, A:min” (i-iv-V-i), where the key of A minor is established. Additionally, after the F# half-diminished chord, the model correctly identifies the next half-diminished chord, which should be a major third below the previous chord. The responsiveness to various chord contexts is valuable in guiding the user to reproduce the CP of interest across keys and in diverse musical contexts. It can enhance the user’s understanding of how the progression sounds and unfolds and thus facilitates their ability to utilize the CP in their compositions or improvisations.

However, two drawbacks are observed. Firstly, Strategy 3 tends to predict a half-diminished chord after most minor chords. This suggests that the model may be overly reliant on the pattern, which could limit its flexibility in generating diverse and contextually appropriate CPs. Additionally, Strategy 3’s generated datasets consist of [eos] tokens directly after the target CP, leading to a bias in the model predicting the [eos] token after the target progression. To address these two issues, future studies may augment the dataset by replacing and extending parts of the CPs using functionally equivalent chords. This approach could help introduce more variety into the training data and mitigate the oversimplified patterns observed in Strategy 3’s predictions. Additionally, modifying a larger foundation model with more advanced fine-tuning methods may enhance the model’s ability to model complex musical relationships and generate more nuanced CPs.

4. Limitations and prospects

This study contains several limitations. To start with, the paper primarily relies on Harte chord symbols as context for generating chord progressions. Future studies could explore incorporating additional contextual information such as beat position, chord voicings, and rhythms to improve the model's ability to discern phrasal structures and generate more nuanced and musically coherent progressions. Secondly, the focus on a single musical piece and CP in this study limits the findings’ generalizability. Future research can examine the method on various musical pieces, use a bigger fine-tuning dataset, and explore the generation of multiple target chord progressions. Additionally, while the study evaluates model performances through several quantitative metrics, studying human participants’ reactions, such as assessment of the musical quality and usability of the generated progressions, can provide valuable insights into how musicians perceive and interact with the model. Last but not least, the study only examined fine-tuning by adjusting all of the trainable units’ weight. More advanced fine-tuning techniques, for example, low-rank adaptation, may be explored in future studies.

In terms of future outlooks, this study has illuminated a novel way to learn harmonic progressions that hold great potential for musicians and composers alike. For instance, musicians may find value in mastering descending fifth sequences in every key to enhance their improvisational skills. To facilitate this learning process, musicians can customize the model with descending fifth chord progressions, enabling them to interactively improvise with the model and receive visualized feedback, such as highlighting relevant keys on a piano keyboard for the next appropriate harmony. Moreover, the ability to fine-tune models with personal improvisation data opens up exciting possibilities for collaboration and knowledge sharing among musicians. Users can train and upload their fine-tuned models, thereby sharing their unique chord progression styles with others. Through real-time interactions with various models, they can explore and learn from each other’s musical styles, fostering a collaborative and enriching learning environment.

5. Conclusion

The study developed a customizable model to facilitate users’ learning of specific chord progressions. Through training a foundation model on the Choco chord corpus and examining three fine-tuning strategies, the study sought to enhance the generation of these CPs. The evaluation of the model’s performance revealed promising results, showcasing an improved generation of musically coherent CPs across diverse contexts. Additionally, the study designed a new mode of generation that can shed light on chord novelty assessment and offer a creative approach to learning and sharing chord styles. These findings underscore the significance of the study in advancing automatic chord progression generation techniques and providing creative tools for musicians seeking to explore and enhance their intuition for harmonies.