1 Introduction

With an increasing requirement of game-theory algorithms recently, more and more work has been done in relevant fields, especially Self-Play algorithms. Self-Play algorithms include algorithms that are developed based on the original Fictitious Play (Brown et al., 1951). After the development over the past years, Self-Play has become a large, and prosperous field. Most Self-Play algorithms are based on Extensive Form Games, while former ones are applicable to Normal Form Games. Extensive Form Games are multiagent games, that involve agents’ sequential interactions. Extensive Form Games also involve a decision tree which describes a set of state $S$ , a set of actions $A$ , and agent’s action $a∈A$ under state $s∈S$ [1].

Self-Play algorithms are ideal when targeting at improving agents’ performance without much outside instructions. It allows agents to start from random policies, combat with itself in each iteration, and improve ability gradually. However, some deficiencies reside in Self-Play algorithms, since they rely on countless iterations and focusing on beating itself. For example, robustness of the agents and calculation amount are significant deficiencies. Over years of development, solutions have been derived to resolve these problems, and each of them has their unique merits.

This paper begins with summaries of some basic and fundamental work, as well as presents of their relationship with relevant fields, and then discusses important Self-Play algorithms. Finally, the paper presents defects in the algorithms and their solutions.

2 Background

Some important works lay foundations for a variety of Self-Play algorithms, including Markov Decision Process, Model-Based Reinforcement Learning, Q-learning, and Fictitious Play. This section briefly summarizes the three algorithms and concepts, as well as presenting their relationship with other concepts.

2.1 Markov Decision Process

A process satisfies Markov Property if each state of the process only depends on the state directly before it. Any process that has Markov Property is a Markov Process, and in which we can apply Markov Decision Process (MDP) to enact the best policy and choose actions. MDP consists of tuples $(S,A,P,R,γ)$ , where $S$ denotes state, $A$ denotes action under the state, $P$ transition probability distribution, $R$ reward of transition from $S$ to $S \prime$ , and $γ$ discount rate. State Value Function calculates the expected future revenue under a certain state, $V=E[\sum _{i=0}^{∞}{γ^{i}}{r_{i}}|{s_{0}}=s]$ . Action Value Function denotes the expected future revenue under a certain state and action $Q=E[\sum _{i=0}^{∞}{γ^{i}}{r_{i}}|{s_{0}}=s,{a_{0}}=a]$ .

2.2 Model-Based Reinforcement Learning

In contrast to Model-Free RL, Model-Based RL applies model to simulate environment. Models are created according to experience using tuple $(S,A,R,{S^{ \prime }})$ , and stores current state, action, revenue gained, and the state after applying the action. Agents benefit from models by thoroughly know about the environment.

Starting with a random policy, the agent interacts with the environment, records models, and stores them in pool $M$ . In each iteration, agent trains $f(s,a)$ to minimize the difference between anticipated state and actual state $s$ . Agent also appends a new model $(s,a,{s^{ \prime }})$ to $M$ every $n$ steps. Figure 1 illustrates the general idea [2].

A successfully trained model set allows agent to have a traversal of all possible states and has a corresponding action to each of the states. However, Model-Based RL requires an inaccessible amount of data to train a good model, since all the trainings are based on datasets. Consequently, two other problems are generated: agents stuck in an attempt of re-exploring familiar environments and has no experience on unknown sections; significant problem of overfitting and less total rewards consequently. Adding a limit on iterations and compelling the agent to focus on less-familiar sections is proposed as a solution [3]. Moreover, combining Model-Based RL and Model-Free RL resolves the overfitting problem, since Model-Free RL allows agents to focus on future rewards [4].

2.3 Q-Learning

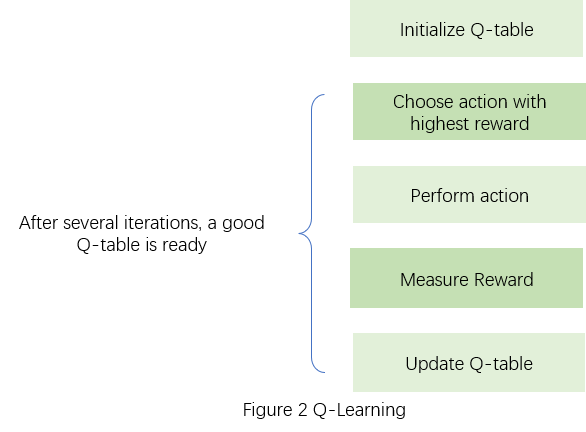
Q-learning is a value-based method, and calculates Q-value based on MDP. Q-learning targets at traversing all possible states and recording the most ideal actions. Starting from a random policy, the agent constantly attempting different actions at each state. After having a Q-table, the agent chooses the best action at each state according to the table, measure its reward, and update Q-value. Figure 2 presents the general idea. Q-learning updates the table using function $Q(s,a)←Q(s,a)+α[R(s,a)+γ {max_{{a^{ \prime }}}} Q({s^{ \prime }},{a^{ \prime }})−Q(s,a)]$ . However, Q-learning requires an inaccessible amount of calculation and attempts for the agent to construct an ideal Q-table, since it applies a “trial-and-error” method to choose actions. Consequently, Q-learning cannot be applied to solve problems in continuous environments, due to the countless possible states. Therefore, Continuous Q-Leaning [5] and Deep Q-Network are presented [6].

2.4 Fictitious Play

The general idea of Fictitious Play [7] is to record adversaries’ strategies and make a coping strategy accordingly. Specifically, the agent chooses the best strategy based on other players’ average strategies, observes, and stores adversaries’ current strategy in the strategy set. Moreover, the agent also updates its own average strategy set.

Fictitious Play is one of the original forms of other Self-Play and fictitious play algorithms, and inevitably has defects. For example, Fictitious Play is inefficient in solving Extensive Form Games. Besides, it is also limited to zero-sum and some constant-sum games. Since Fictitious Play relies Nash Equilibrium to resolve problems, it cannot guarantee best solutions.

3 Amelioration of Fictitious Play

The idea of Fictitious Play is not broadly applied until more improvements are made, because Fictitious Play can only be used in normal form games, which are generally less popular forms. and an excessive amount of calculation is required to train an ideal agent. However, the idea of recording and learning from opponents’ strategies has inspired various algorithms, which in turn are making the field of Self-Play prosperous.

3.1 General Fictitious Self-Play and Neural Fictitious Self-Play

General Fictitious Self-Play (FSP) is an enhancement of Fictitious Play, which cannot be applied to Extensive Form Games. Similar to Fictitious Play, FSP also consists of two sections. Firstly, it records opponents’ strategies and uses the data to anticipate their current strategy. Secondly, it chooses a coping strategy based on its own past strategies. Finally, it updates all the strategy datasets. FSP is ameliorated based on Extensive-Form Fictitious Play in order that the algorithm can be adapted in various situations and under different machine learning frames. Moreover, a data generator is also added to produce more general samples based on known datasets. Specifically, FSP attempts to mix the agents’ average strategies with best response strategies, ${σ_{k}}= (1−{η_{k}}){π_{k−1}}−1+{η_{k}}{β_{k}}$ , where ${σ_{k}}$ is the sampling strategy, ${π_{k−1}}$ is the agent’s average strategy in the former episode, ${β_{k}}$ is the best response strategy, and ${η_{k}}$ is the coefficient of mixing the two strategies. [8]

Neural Fictitious Self-Play (NFSP) is a further enhancement of FSP, so that neural networks and Q-learning can be used to improve efficiency. Besides, $ϵ−greedy$ method is also used in the data generator section of FSP.

3.2 δ Fictitious Self-Play

δ Fictitious Self-Play (δ-FSP) focuses on improving opponent sampling based on how new the samples are. δ-FSP uses coefficient $δ$ to determine how many latest models are sampled while $(1−δ)$ determines how may earlier models are sampled. Specifically, setting $δ=1$ allows the agent to concentrate on the latest models, and $δ=0$ requires it to sample uniformly over the entire past models. Experiments proves that certain agents in some games require a larger value of $δ$ since earlier models of opponents are not strong enough, whereas other games require smaller value of $δ$ because either the models are generally constant or the training is aiming at improving the agent’s robustness. [9]

3.3 Prioritized Fictitious Self-Play

Prioritized Fictitious Self-Play (PFSP) aims at choosing the best-fit opponents for the agent. Instead of traversing the entire model set, or simply choosing between the latest and the earlier models, PSFP chooses models based on the probability of beating a model. Firstly, the agent $A$ determines the probability of beating the models in dataset $D$ . Then, $A$ chooses a certain model $M$ from $D$ with probability $p=\frac{f(ℙ[A beats M])}{\sum _{m∈D}f(ℙ[A beats m])}$ , where $f$ is certain function, and is determined as $f=x(1−x)$ by Oriol et al. in order to help the agent to focus opponents at similar level. [10]

4 Problems and Solutions

Similar problems lie in each generation of Self-Play, and different algorithms have proposed distinct solutions. Most salient problems include requirement of robustness, and excessive calculation amounts. This section analyzes the two problems in general, and then presents how does each algorithm solves them.

4.1 Defect of Robustness

Robustness denotes how universal a set of strategies is. Algorithms that mainly rely on sample sets are especially prone to have defects in robustness since they only depend on certain samples that cannot necessarily represent the whole. Similarly, Self-Play algorithms also have this problem because of their dependence on model samples. Most of the Self-Play algorithms improve the performance of agents by requiring them to beat model samples. However, in some games there is no universal strategies that guarantee agents’ victories over most opponents. Consequently, it is important for the algorithm to adjust agents’ strategies so that they do not focus on only one opponent. [11]

Approaches targeting at improving robustness include using noisy stochastic gradient updates and mixing best response strategy with average strategies. NFSP uses $ϵ−greedy$ to allow agents to choose from strategies, besides, it also adds random exploration to impact the response strategy with a random factor. FSP uses coefficient $η$ to set the mixture of average strategy and best response strategy.

4.2 Excessive Calculation

Excessive calculation is a significant defect in most Self-Play algorithms, because of their reliance on repetitive combats with past models. For example, one great problem of Fictitious Play is too much calculations, and hence inapplicable in Extensive Form Games. The general idea of reducing computations is to focus on certain opponents, instead of traversing all of them.

One of the most important solutions is put forward by PFSP. It uses function $f$ and probability $ℙ$ , which determines the possibility of beating a certain model, to reduce calculation amount. Specifically, PFSP chooses which category of models the agent focuses on by changing $f$ . This allows agent to concentrate on either easier or harder opponents rather than the entire model set. Besides, δ-FSP solves the calculation deficiency by choosing from either latest or earlier models.

5 Conclusion

This paper firstly discusses the basis of Self-Play algorithms, including MDP, Model-Based RL, Q-learning, and Fictitious Play. Then the paper summarizes major Self-Play algorithms. Finally, discussions of defects and solutions are included. Future ameliorations will be achieved by learning from other fields and introduce algorithms to Self-Play. For example, Deep Q-learning, as an enhancement of Q-learning by introducing Deep Neural Network, can be taken into consideration and help to improve sample efficiency.