1. Introduction

Material science, a multidisciplinary field intersecting physics, chemistry, and engineering, is continually faced with challenges, from developing new materials with desired properties to understanding complex processes at the atomic or molecular level. Traditional computational methods have limitations, largely due to the immense computational resources required to accurately simulate and predict material behaviors. As machines' computing power was limited, exploring the vast 'material universe' seemed a near-impossible task. However, with the advent of machine learning (ML), researchers have made significant strides in this field, changing the way we understand and design materials. Machine learning has been integrated since the late 1990s and early 2000s. During this period, basic techniques, including regression models, were employed for various purposes, such as predicting material characteristics based on specific input variables. Then, the real revolution started in the mid-2010s, when advances in hardware technology and the advent of deep learning allowed researchers to build more complex and accurate models. By leveraging large datasets (termed "material informatics")., researchers began to use deep learning techniques to make predictions about material behaviors, properties, and suitable conditions for various applications. Initially, the focus of machine learning in materials science was mainly predictive: given a material's composition and structure, what will its properties be? what should a material's composition and structure be? Nowadays, this method has gone far beyond that. For instance, it is used for guiding experiments and developing new materials, optimizing manufacturing processes, and simulating and understanding complex phenomena that are hard to investigate with traditional computational methods. The ongoing developments in machine learning, such as reinforcement learning and transfer learning, promise to further revolutionize the field of materials science. Researchers are now working towards creating a closed-loop system where machine learning models can guide experimental procedures and the experimental results can further refine the models in a continual learning process. As machine learning continues to innovate, we can expect even more significant breakthroughs in materials science in the future. This review is organized as follows. In section \Rmnum{2}, we give a brief introduction of the density functional theory, and then in section \Rmnum{3} the combination of DFT and ML in materials science is summarized. Various models of machine learning with DFT are reviewed. In section \Rmnum{4}, we summarize the application status of various models in material discovery and performance prediction. To be noted, this article aims to study materials science issues from the perspective of machine learning models.

2. Density functional theory

Density Functional Theory (DFT) is used for analyzing the electronic structure of atoms, molecules, and solids. Its development includes the following key milestones:

• Thomas-Fermi model (1927): Thomas and Fermi established DFT's foundation using a semiclassical approach for atoms and solids.
• Hohenberg-Kohn theorems (1964): Hohenberg and Kohn created DFT's framework, proving ground state energy is determined by electron density and an energy functional exists with a minimum value at ground state density.
• Kohn-Sham equations (1965): Kohn and Sham introduced Kohn-Sham equations, simplifying the many-body problem using non-interacting single-particle equations.
• Exchange-correlation functionals (1970s-1980s): Researchers developed approximations, such as LDA, GGA, and hybrid functionals, to enhance DFT accuracy.
• Efficient algorithms and computational advances (1980s-present): Improved numerical algorithms and computer hardware enabled more accurate and practical DFT calculations.
• Time-dependent DFT (1980s-present): This extension allows studying time-dependent perturbations, with applications in spectroscopy, photochemistry, and excited state dynamics.
• Multiscale modeling (1990s-present): Researchers combined DFT with less computationally demanding methods, like classical molecular dynamics, for large systems or long timescales.

In short, DFT is popular in computational quantum chemistry, materials science, and condensed matter physics due to its accuracy and efficiency. Ongoing developments aim to improve functionalities, enhance algorithms, and expand applications. Next, this article will elaborate on the principle of DFT, the combination of DFT and ML, and the ML method combined with material science, summary, and prospect. Since some heuristic algorithms, such as Particle Swarm Optimization and Genetic Algorithms, are not machine learning algorithms per se, these will not be included in this article. However, heuristic algorithms are also widely used in the field of materials science. For example, Song et al. used PSO, GA, and Beetle Antennae Search (BAS) to optimize the mixing ratios of modern cementitious materials [1]. Sahimi summarized the use of various heuristic algorithms in the reconstruction, optimization, and design of heterogeneous materials and media [2]. Density Functional Theory (DFT) has emerged as a fundamental pillar of modern quantum chemistry and solid-state physics, offering effective solutions to electronic structure problems. While its origins can be traced back to the early work of Thomas and Fermi in the 1920s, DFT achieved significant breakthroughs with the formulation of the Hohenberg-Kohn (HK) theorem in 1964 and the subsequent development of the Kohn-Sham (KS) equations in 1965. A key focus of DFT lies in approximating the exchange-correlation functional, denoted as  \(E_{xc}[\rho]\) , which represents the distinction between the actual energy and the classical energy of the system. Nowadays, machine learning has become increasingly important in DFT calculations for several reasons including computational cost reduction, speeding up convergence, handling complex systems (strong correlation, hybrid functionals), high-throughput screening, and interpretable models. By integrating ML and DFT, researchers can accelerate the discovery of new materials and molecules, as well as gain a deeper understanding of their properties.

3. Machine learning methods

Machine learning has emerged and developed for a long period. Selecting the appropriate machine learning algorithm is essential when constructing a machine learning system since it can significantly influence the accuracy of predictions and the system's ability to generalize. There is no single algorithm that fits all problems, as each algorithm has a specific area of application. When working with datasets, the approach taken depends on whether the data is labeled or unlabeled. If the data has corresponding labels, a supervised learning algorithm is used to identify the mapping between data points and their labels. However, if the data lack labels, unsupervised learning techniques are utilized to uncover patterns and structure within the datasets. Xie and Grossman developed a crystal graph convolutional neural network (CGCNN) for predicting material properties using supervised learning [3]. In molecular dynamics simulations, the forces that govern the interactions between atoms are usually described by the so-called "force field". The accuracy of the force field is paramount for the reliability of the MD simulation results. Using supervised learning to "learn" the force fields from data. Zhang et al. introduced the DeePMD method, which uses deep learning models to represent atomic interactions and model potential energy surfaces, making accurate predictions about atomic forces in MD simulations [4]. Apart from this, Sch¨utt et al. introduced SchNet, a deep learning architecture for quantum chemistry [5]. The model is designed to capture interactions in molecules and condensed matter, providing highly accurate predictions of energy and force fields for MD simulations. The work by Ward et al. showcases the application of unsupervised machine learning in predicting the characteristics of inorganic materials [6]. They employ a clustering algorithm to group materials based on their local chemical environments, without using any prior knowledge about their properties. This unsupervised approach helps identify underlying patterns in the datasets, which can then be used to guide the development of more accurate and efficient predictive models.

3.1. Regression

Machine learning algorithms in materials science can be categorized into three main types: probability estimation, regression, and clustering/classification. Probability estimation algorithms are typically applied in the search for novel materials, while regression, clustering, and classification algorithms are used to forecast material properties at both macro and micro scales. Many methods of machine learning include regression methods, such as support vector machines, artificial neural networks, multiple linear regression, and so on. Specifically, SVR is used for predicting various material properties, such as electronic, optical, mechanical, and thermal properties. It can handle nonlinear relationships, small datasets, and high-dimensional data effectively, making it suitable for materials science applications. ANNs are employed for modeling complex, nonlinear relationships between material features and properties, such as electronic structures, phase stability, and mechanical properties. They offer flexibility in architecture and can be fine-tuned for specific tasks. MLR is applied to predict material properties based on linear relationships between material descriptors and target properties. It provides valuable insights into the relationships between material features and properties but may be limited when dealing with nonlinear relationships or high-dimensional data.

3.1.1. Support Vector Regression.

Although ANNs have shown improved prediction capabilities compared to linear regression, they still suffer from certain weaknesses, such as the need for many controlling parameters and the danger of overfitting. A method developed by Fang et al. utilizes real-value genetic algorithms (RGAs) to determine the optimal hyperparameters of SVR, resulting in the most accurate and adaptable prediction of atmospheric corrosion of zinc and steel [7].

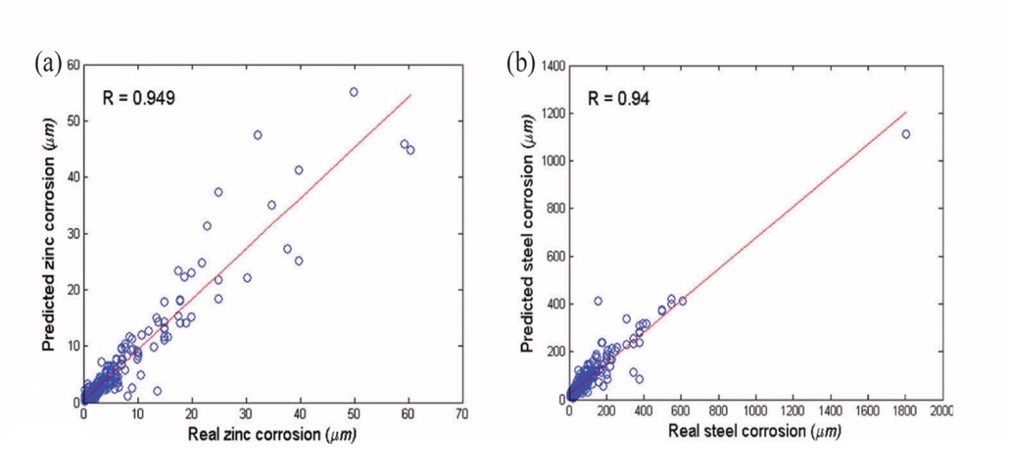
Desu et al. conducted a study on utilizing SVR to model the correlation between flow stress and various factors like strain and temperature in materials [8]. Olatunji and Taoreed employed a hybrid approach of Support Vector Regression (SVR) and Genetic Algorithm (GA) to accurately estimate the energy gap of doped spinel ferrite nanoparticles, taking into account the size of the particle and the crystal lattice parameter as key inputs for the model [9]. Owolabi and Mohd combined SVR with a gravitational search algorithm (GSA) in predicting the energy gap of doped bismuth ferrite compounds, which is a typical non-linear problem [10].

3.1.2. Artificial neural network.

Nikoo et al. used ANN to predict the compressive strength of concrete [11]. The model combines ANN and evolutionary search procedures, such as genetic algorithms (GA), to optimize the number of layers and nodes, and weights in the ANN models. The main aim of these models is to estimate the compressive strength of concrete. To enhance their accuracy, a GA is employed. After optimization, the accuracy of the ANN model is gauged against the Multiple Linear Regression (MLR) model. Bio-ceramics play a pivotal role in repairing and reconstructing damaged or diseased human body parts. Altinkok and Koker implemented an ANN to estimate the alumina percentage in ceramic mixed components and the porosity volume fraction [12]. As depicted in Fig 2, the ANN structure is designed with an input layer, a hidden layer, and an output layer. The input layer takes in the SiC amount, whereas the output layer yields two pieces of information: the alumina percentage in the produced ceramic mixed components and the porosity volume fraction in the ceramic cake. The number of neurons in the hidden layer is determined by experiments.

The model is trained using experimental samples obtained by experiments, employing the gradient descent learning algorithm to compute the synaptic weights and biases. After calculating the weights and biases, they are used to determine the OUT and NET values. These values are then subject to an activation function. The outputs from the hidden units become inputs for the subsequent layer units.  \(NET_j\)  represents the net interval activity of neuron j. Upon training the ANN with experimental samples, it exhibits reasonably accurate outputs for some of the trial inputs in the test set. Consequently, ANN holds great promise for conducting studies in material science.

3.2. Probability Estimation

3.2.1. Expectation Maximization.

Expectation Maximization (EM) is a statistical method that is widely used in many fields, including materials science. The main goal of EM is to estimate the parameters of a statistical model when data is missing or incomplete. In materials science, EM has been used for a variety of applications including the analysis of X-ray diffraction patterns, the characterization of microstructures, and the modeling of molecular dynamics simulations. Specifically, EM has been used to analyze X-ray diffraction data to determine the atomic structure of a material. The diffraction pattern contains information about the positions of atoms in the crystal lattice, but the positions are often not directly observable. In molecular dynamics simulations, EM has been used to estimate the energy landscape of a system. The energy landscape describes the system's potential energy as a function of the positions of the atoms. EM can be used to estimate the energy landscape from a set of simulations with different starting configurations. In a study conducted by Kujawińska et al., they explored an alternative approach to selecting materials for the Submerged Arc Welding method process [13]. They utilized the non-hierarchical Expectation Maximization (EM) method. Li et al. used the expectation-maximization algorithm to analyze their data to reveal different mechanical phases, considering shale Young’s modulus and hardness [14].

3.2.2. Naive Bayes.

In materials science, Naive Bayes is a popular machine learning algorithm that has been applied to a variety of tasks, such as materials discovery, materials property prediction, and materials classification. Based on Bayes' theorem, it assumes that features are independent, This makes it not only easy to implement but also extremely computationally efficient. To give an intuitive picture, we provide an example here to show how Naive Bayes was applied in materials science. In the area of materials discovery and property prediction, for example, In their study, Ward introduced a machine learning framework that can be used for predicting the properties of various inorganic materials [15]. Although Naive Bayes does not outperform other methods in this study, it still achieves reasonable accuracy in predicting the properties of inorganic materials. This highlights the potential of Naive Bayes as a computationally efficient and straightforward technique for material property prediction.

3.3. Classification and Clustering

3.3.1. K-nearest neighbors.

K-Nearest Neighbors (KNN) is a supervised machine learning algorithm that classifies a data point based on the majority class of its 'k' nearest neighboring data points in the feature space. It is simple, easy to implement, and works well for problems with a small number of dimensions and many training samples. The KNN algorithm is also widely used in material science. To predict the phase of high-entropy alloys (HEAs), Ghouchan et al. developed an algorithm that utilizes a graph-based KNN method [16]. By selecting the K-nearest neighbors in the HEA network, the algorithm is able to accurately predict the phase through plurality voting. In order to make predictions, the algorithm initially detects the position and then connects the new compound in the HEA network. It then does the prediction by finding the closest neighbor in the network. The accuracy of the proposed approach was compared with six other methods, and it outperformed all of them, which is shown in Fig 3.

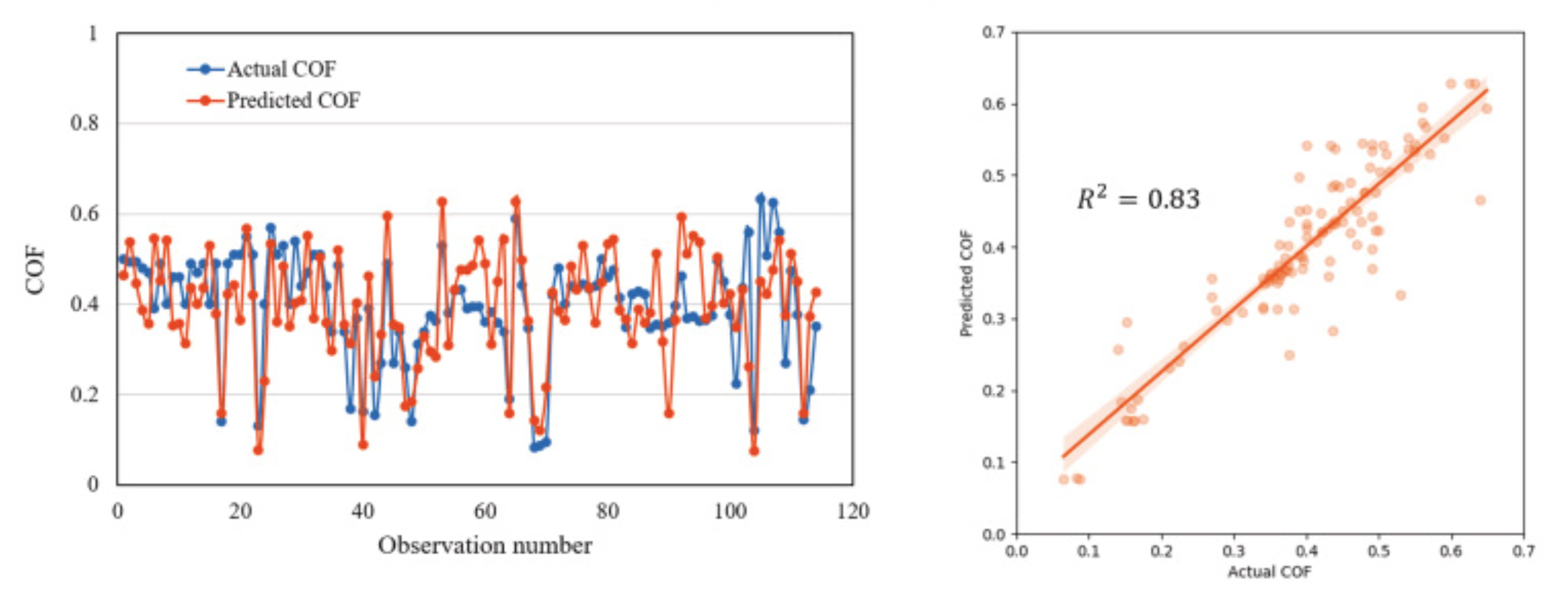
Mitra et al. examined the application of KNN in forecasting the formation of solid solution diborides within multi-component ceramics [17]. The selection of the KNN model was driven by its ability to maintain a balance between model performance and complexity, making it an effective tool for projecting new compositions. In Wen et al. study, KNN is applied, along with other ML algorithms, to assist in the design of high-entropy alloys (HEAs) with specific properties [18]. In microstructure analysis, KNN is utilized to analyze and classify material microstructures based on their features, such as grain size, grain orientation, and phase distribution. By leveraging the similarities between different microstructures, KNN can provide valuable insights into material properties, processing conditions, and performance. In Hasan et al. research, K Nearest Neighbor (KNN) algorithm was used for predicting the coefficient of friction (COF) of aluminum alloys from the material and tribological test variables [19]. The specific data are in Figure 3. The conclusion is that the KNN algorithm emerged as superior in predicting the COF of aluminum alloys in this study.

3.3.2. Decision Tree.

Decision trees are a popular and versatile class of machine learning algorithms used for classification and regression tasks. They are easy to interpret, can handle various data types, and are relatively efficient in computation and memory. A Decision Tree is a flowchart-like tree structure in which each internal node represents a feature (or attribute), each branch represents a decision rule, and each leaf node represents an outcome, like the structure in Fig 4. The goal is to recursively partition the input space, creating a tree structure that accurately classifies or predicts the output for new samples.

The decision tree algorithm constructs a tree-like model by recursively partitioning the input data into subsets based on the most discriminative features, ultimately leading to a prediction or decision. Due to their interpretability and ability to handle non-linear relationships between variables, decision trees have been successfully applied to tackle complex problems in material science. By constructing predictive models using available data, decision trees can guide the search for materials more efficiently, significantly reducing the number of experiments needed to identify high-performance materials. These methods can be combined with other machine learning techniques, such as active learning or adaptive design, to iteratively update the models and improve their predictive capabilities as new data is acquired. Increasing energy density and efficiency in rechargeable batteries is a goal in material science. The process of growing the decision tree involves dividing the data into two parts while minimizing the increase in Gini impurity. Also, the tree shouldn’t grow too large to avoid overfitting. After the tree is fully grown, it is pruned to the point where the cross-validation error is at its lowest. As for process optimization, Theeda et al. applied a decision tree algorithm to optimize the process parameters of laser additive manufacturing [20]. They consider various process parameters, such as laser power, scanning speed, and layer thickness, and their effects on the material properties, including relative density and tensile strength. The decision tree model is trained using experimental data and then used to predict the optimal process settings for producing high-quality parts. The model's predictions are verified by experimental tests, demonstrating the effectiveness of the decision tree algorithm in LAM process optimization. The decision tree algorithm proves to be a viable approach in dealing with this. complex. computations involving vast amounts of data, particularly in the production of coal tar-based CMs. As shown in Zhou et al. study, the model accurately identified the crucial variables that affect CM preparation, namely the raw material type, reaction temperature, and reaction time, in a specific order [21].

4. Conclusion and outlook

To summarize, this article painted a roadmap for the development of machine learning in materials science, we hope it can benefit researchers working on materials discovery with desired properties. ML is used extensively in materials science, guiding experiments, optimizing manufacturing processes, and simulating complex phenomena. Then it explores the potential of newer techniques like Capsule Neural Networks, Echo State Networks, and Quantum Machine Learning in materials science. Here we show the recent materials science investigation utilizing machine learning algorithms for various applications, including composite design, molecular dynamics, phase prediction, and property prediction. By integrating ML and Density Functional Theory (DFT), researchers can accelerate the discovery of new materials and molecules and gain a deeper understanding of their properties. However, there are many methods of machine learning, some of which are not currently applied in materials science. To give some pointers, we outlook these methods as follows:

• A capsule neural network signifies a type of artificial neural network (ANN) utilized in machine learning, which excels at effectively modeling hierarchical relationships. This method is conceived to emulate the organization of biological neurons more accurately.
• Echo State Networks (ESNs) are a special type of Recurrent Neural Networks (RNNs) suitable for processing time series data. The core idea of ESNs is to fix a large part of the neural network to a random state, and only train the connection of the output layer, which can greatly reduce the complexity and computational cost of training. In cases where time-dependent properties are studied in materials science, researchers might prefer alternative RNN architectures like Long Short-Term Memory (LSTM) or Gated Recurrent Units (GRU), which have a more established reputation.
• Quantum Machine Learning (QML) is an emerging interdisciplinary domain that merges quantum computing with machine learning. Leveraging the principles of quantum mechanics, such as superposition and entanglement, quantum computers demonstrate superior computational efficiency over classical computers for specific problem-solving tasks. QML algorithms leverage the unique capabilities of quantum computers to improve the efficiency and effectiveness of machine learning tasks. Quantum computers can potentially provide exponential speedup for problems like searching unsorted databases, factoring large numbers, or simulating quantum systems.

Overall, it is important to note that the field of machine learning is constantly evolving, and as those methods mentioned above continue to be researched and refined, their potential advantages and applications in materials science may become more apparent. Over time, they could gain more traction in the field as researchers become more familiar with their capabilities and potential benefits.