1. Introduction

The reliability of engineered structures is of paramount importance. It depends on sound design and careful construction to ensure that the actual state of the structure upon completion is consistent with the design expectations. However, over time and with continued use of the structure, its actual state often changes due to various factors, including structural deterioration, disaster damage, and overloaded operations. Historically, major accidents due to structural damage have been commonplace, such as the 2013 collapse of the Rana Plaza building in Dhaka, Bangladesh. The eight-storey commercial building had been added to multiple floors without permission and had serious building quality issues. On April 24, 2013, the building suddenly collapsed, with tragic consequences of at least 1,127 deaths and over 2,000 injuries[1]. On October 30, 2022, local time, a cable-stayed bridge collapsed in Gujarat, India, with about 500 people on board at the time of the collapse, and about 100 people trapped in the water, resulting in a large number of casualties[2]. These accidents show that safety and reliability of large and important structures such as bridges, buildings and oil platforms must be given high priority. In the process of structural use, regular inspection and maintenance are required to detect and repair potential damages and hidden dangers in a timely manner. The current research direction on structural damage identification is mostly oriented to the centralized processing of large amounts of data. For example, Sunfeng You based on environmental excitation on the bridge vibration characteristics and damage identification[3]. WeiJian Yi et al. based on Bayesian statistical inference on the damage diagnosis of frame structures[4]. Yuyao Cheng monitored structural health using long-scale fiber optic sensing technology[5].

In this paper, the basic laws of parameter updating are explored through the application of the Bayesian updating method in structural damage identification. The main advantages lie in its capability to rigorously fuse the original data, providing probability estimates of each possible damage state, enabling accurate prediction and categorization of damage situations.The causal relationship and conditional independence between variables are utilized to simplify the joint probability model and improve the computational efficiency, while relying on the principle of virtual work to validate the data for the displacement calculation. The damage identification process is made more efficient and reliable.

2. Methodologies

2.1. Structural Damage Research Methods

Since the 1940s, structural damage identification has become a hot spot of academic research. Over the decades, with the expansion of civil engineering construction scale and the advancement of computer technology, structural damage identification methods have made remarkable development. For example, Sheng Zhang analyzed the reliability of concrete gravity dam system based on structural performance feedback[6], Fuyu Bai identified and assessed the state of seismic damage of wood-framed ancient buildings [7] Frans Richard et al. used the third-level method to identify the damage of space truss structures [8] These methods are constantly innovated and developed, which not only improve the accuracy and efficiency of damage identification, but also provide a new method for the safety assessment and maintenance management of civil engineering structures. These methods improve the accuracy and efficiency of damage identification and provide strong technical support for the safety assessment and maintenance management of civil engineering structures.

Structural damage research methods mainly include dynamic parameter identification and static parameter identification. Dynamic parameter identification focuses on analyzing the dynamic characteristics of a structure through its vibration signals or sensor data, such as modal analysis and frequency domain analysis, which are effective in identifying structural damage and evaluating its extent. Static parameter identification, on the other hand, relies mainly on the static properties of the structure, such as stiffness characteristics, and identifies damage by means of loading experiments, which has the advantage of being easy to operate, economical and fast, and predicting the remaining life of the structure. Structural damage identification can be made more accurate and dependable by using these two techniques separately or in combination. Deterministic input-output and mapping connections are the foundation of the somewhat idealized deterministic method to structural damage identification. However, in the actual process of structural damage diagnosis, many uncertainty factors are often difficult to be considered comprehensively in deterministic methods, thus limiting their wide application in engineering practice.

Recognizing that the uncertainty factors (e.g., observation, modeling, etc.) of structural damage identification in actual engineering should not be neglected, the structural damage uncertainty identification methods have been gradually developed, and nowadays they are mainly focused on two directions: one is based on Bayesian updating of the identification method, and the other is based on the fundamentals of Monte Carlo sampling method.

2.1.1. Recognition method based on Bayesian updating Bayesian updating is a probabilistic inference method based on Bayes' theorem, which allows us to update the prior probability distribution as new evidence emerges, resulting in a more accurate posterior probability distribution. In structural engineering, we can consider the a priori information as a general understanding of the structure's performance, such as design parameters, material properties, etc.; and consider the new evidence as the actual use of the structure, monitoring data, etc. Through Bayesian updating, we can combine this a priori information with new evidence to provide a more accurate assessment of structural performance. Bayesian updating allows flexible integration of the prior. In practical structural engineering problems, combining the a priori with observed data produces highly accurate and robust models. Also Bayesian updating can dynamically update the model. In structural engineering, a structure's performance changes with time and changes in the external environment. Bayesian updating can dynamically update the model parameters based on new observations to more accurately reflect the current performance of the structure. The Bayesian formulation is a mathematical expression of the Bayesian principle, specifically:

\( P(B/A)=\frac{P(B/A)*P(A)}{P(B)} \) (1)

where P(A/B) denotes the probability that event A occurs after event B is observed; P(B|A) denotes the probability that event B occurs given that event A occurs; and P(A) and P(B) are the a priori probabilities of event A and event B, respectively.

2.2. The basic principle of Monte Carlo sampling method

The model identification method based on Monte Carlo Simulation (MCS) has attracted much attention because of its powerful statistical inference capability. The method provides an effective way for structural damage identification by simulating a stochastic process that generates a large number of possible sample results, thus estimating the statistical characteristics of the model parameters. This approach begins by building a finite element model that reflects the mechanical and response characteristics of the structure and identifying the key sampling parameters. Subsequently, Monte Carlo sampling techniques are utilized to generate many parameter samples to simulate the structure's response in different states. By statistically analyzing these response samples, the damage of the structure can be identified. This method is flexible and highly accurate, but is computationally intensive and may be limited by a priori information. In structural damage identification, Monte Carlo sampling methods can be used to model the randomness of the structural response and thus estimate the range of variation of structural parameters (e.g., stiffness, mass, etc.) to identify structural damage.

From the definition of probability, It is well known that the frequency with which an event occurs across a large number of trials can be used to estimate its likelihood. In cases where the sample size is sufficiently high, the frequency with which an event occurs can also be regarded as its probability. As a result, many random samples of the random factors influencing its dependability can be obtained. To find out if the structure fails, these sample values can then be entered into the functional equation in a group. Ultimately, it is possible to derive the structure's failure probability from it. This analytical concept is the foundation of the Monte Carlo method.

There are statistically independent random variables

\( {x_{i}}(ⅈ=1,2,3,⋯,k) \) (2)

Their corresponding probability density functions are

\( {f_{{x_{1}}}},{f_{{x_{2}}}},…,{f_{xκ }} \) (3)

The functional equation is

\( z={g_{({x_{1}},{x_{2,⋯,xk}})}} \) (4)

First, generate N sets of random numbers x1, x2, ..., and xk values based on the corresponding distribution of each random variable and compute the function. Function values \( {z_{i}} \)

\( {Z_{i}}=g({x_{1}},{x_{2}},…,{x_{k}})(i=1,2,…,N) \) (5)

If one of the groups of L random numbers corresponds to the value of the function Zi ≤ 0, then when N → ∞, according to Bernoulli's Large Number Theorem and the properties of normal random variables there are: the probability of structural failure, the reliability index.

Establishing various estimators is equivalent to examining and registering the results of simulation experiments, from which the problem's solution is obtained[9]. The idea of the Monte Carlo method can be seen from the fact that the method avoids the mathematical difficulties in the analysis of structural reliability, regardless of whether the state function is nonlinear or not and whether the random variable is nonnormal or not, as long as the number of simulations is sufficiently high, a more accurate probability of failure and reliability index can be obtained. The results are more accurate and easy to program due to the simplicity of the idea.

2.3. Classification of objects for identification of structural damage

Parameter identification plays a crucial role in structural engineering, and according to different identification strategies, it can be roughly divided into two categories: static parameter identification and dynamic parameter identification. These two types of methods have their own characteristics and play different roles in practical applications.

Dynamic parameter identification mainly depends on the dynamic response of the structure, i.e., the dynamic properties such as mass, stiffness, and damping. These dynamic characteristic parameters can be obtained by applying certain dynamic excitation and measuring the structure's response. For example, Zhenqiang Jiang et al. identified the dynamic characteristics of offshore wind power monopile foundation[10] , and Longwei Zhang et al. used the dynamic response generated by a crossing vehicle on a bridge to quickly identify the axle mass of the vehicle[11]. However, dynamic parameter identification is less sensitive and time-consuming in determining damage locations and dealing with complex structures. It also requires complex equipment and is costly, so it needs to be combined with other methods to improve accuracy and reliability.

In contrast, static parameters are more concerned with the static properties of the structure. By applying static loads and measuring the displacement response of the structure's stiffness distribution and changes can be deduced. Static parameters show significant advantages in structural damage identification compared to dynamic parameters. Firstly, static testing is simple and economical, without the need for complex equipment and test conditions, which makes the testing process more convenient and economical. Secondly, static parameters have high measurement accuracy and can provide accurate damage identification information in a stable environment. In addition, static testing methods can identify damage to structures, assess damage to a wide range of materials, and evaluate the remaining life of a structure. These advantages give the static parameters important application value in structural damage identification. In practical application, the advantages and disadvantages of static and dynamic parameters need to be considered comprehensively to select the most suitable damage identification method.

In summary, the static parameter identification method has unique advantages in the field of structural damage identification and has gained more and more attention in practice from researchers. In practical application, suitable identification methods should be selected according to specific engineering needs and conditions in order to realize accurate assessment and prediction of structural damage.

3. Analysis of results

For the complex task of structural damage identification, a combination of OpenSees software, Monte Carlo sampling principles, Bayesian updating methods, and virtual work principles can be used to construct an efficient and accurate analysis framework. The following is a detailed description of this process.

First, OpenSees software, an open system for earthquake engineering simulation, provides a powerful computational tool for structural damage identification. Developed by the University of California, Berkeley, and other institutions, OpenSees is primarily used to simulate seismic responses in structural and geotechnical aspects. Its wide range of material models, cells, and solution algorithms allow it to accurately simulate the nonlinear response of various complex structures under external forces such as earthquakes. In structural damage identification, OpenSees can be used to numerically model the structure to be analyzed and simulate the structural response under different damage states. In structural damage identification, Monte Carlo methods can be used to estimate the posterior distribution of structural physical parameters. Since the posterior distributions of structural physical parameters are often complex and high-dimensional, it is very difficult to directly solve their exact forms. In contrast, Monte Carlo methods can approximate the statistical properties of the posterior distributions by extracting a large number of samples, thus providing important information for structural damage identification.

On the basis of Monte Carlo sampling, the Bayesian updating method is used to update the prior distributions of structural physical parameters. Through continuous iteration and updating, the Bayesian method can gradually approximate the real values of structural physical parameters, thus realizing the effective structural damage identification. The modeling information is shown in Figure 1 below, with the damaged bars in red.

Figure 1. Bayesian update based damage identification method

Meanwhile, the principle of imaginary work plays an important role in calculating structural displacements. Calculation of displacement by virtual work is a method of structural mechanical analysis, which is based on the principle of virtual work, and solves the real displacement of a structure under the action of external force by considering a hypothetical small displacement (i.e., virtual displacement) that corresponds to the actual displacement, and calculating the work done by external force and internal force (i.e., virtual work) under this virtual displacement. This method is applicable to complex structural systems, i.e., the deformation and displacement of the structure can be determined by comparing the virtual work of the external force and the virtual work of the internal force, which provides an important means for the mechanical analysis and optimal design of the structure. The principle of virtual work is a basic principle in analytical mechanics, which utilizes the concepts of false displacements and ideal constraints to discuss the conditions for a mechanical system to be in equilibrium. In structural damage identification, the principle of virtual work can be used to calculate the displacement response of the structure under different damage states. The location and extent of damage to the structure can be recognized by comparing the displacement response under different damage states. The application of the virtual work principle makes the calculation of structural displacement more accurate and efficient, and provides a strong support for structural damage identification.

In the specific implementation, OpenSees software can model the structure to be analyzed and simulate the structural response under different damage states. Then, the Monte Carlo method is used to extract many samples to estimate the posterior distribution of the physical parameters of the structure. Then, the Bayesian updating method is utilized to update the prior distribution according to the observed data to obtain a more accurate posterior distribution. Finally, the displacement response of the structure under different damage states is calculated using the principle of virtual work, and the damage location and degree of the structure is identified by comparing the displacement response

By modeling the structure in OpenSees to simulate the damage environment, the update results by the above method are shown in Figure 2 Figure 3. In this update, it can see the actual data in Table 1.

Table 1. Bayesian update based damage identification method

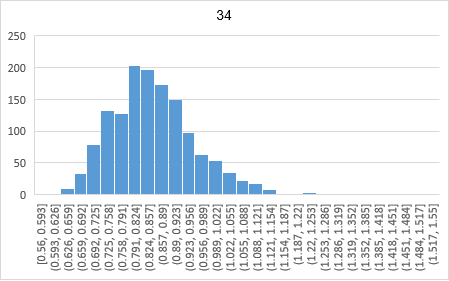
Figure 2. Bayesian update based damage identification method

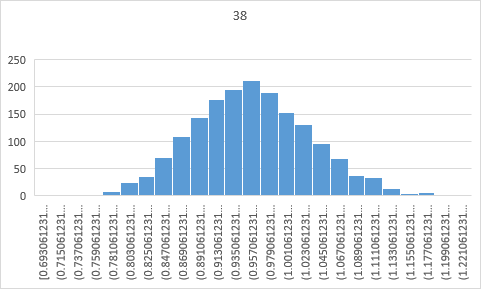
Figure 3. Bayesian update based damage identification method

Comparison between Figure 2 Figure 3 with the predicted data after Bayesian updating. The effect of the update shows that the Bayesian approach significantly adjusts the initial probability distribution to match the actual data more closely. This adjustment reflects the impact of new evidence on the original hypotheses, thus making the predictions more accurate. Specifically, the updated data distribution is more centralized, reducing uncertainty and improving the results' prediction accuracy. In addition, there may be some outliers or extreme cases in the actual data, and the Bayesian approach can effectively take this information into account to avoid overfitting or ignoring important details.

4. Conclusion

This method combines the OpenSees software, the statistical properties of Monte Carlo sampling, the inference ability of Bayesian updating method and the mechanics of virtual work principle to provide a comprehensive and effective solution for structural damage identification. Through continuous iteration and optimization, the method can gradually approximate the real situation of structural damage, providing an important basis for structural safety assessment, repair, and reinforcement. Overall, Bayesian updating has shown remarkable effects in data analysis. It not only makes the predicted data closer to the actual data, but also improves the accuracy and reliability of the prediction. This updating method has obvious advantages in dealing with complex data and uncertainty, and can provide more accurate and comprehensive information support for decision makers. Therefore, Bayesian updating has important application value in the field of data analysis and prediction. With the continuous development of technology and in-depth research, the Bayesian updating method will continue to be optimized, and the existing improved algorithms, such as the component-by-component adaptive Metropolis-Hastings (MH) sampling technique, have significantly improved the computational efficiency and convergence speed. With further improvement in computational power and deeper algorithmic research, more efficient and stable sampling algorithms are expected to be developed to make the application of Bayesian updating in structural damage assessment more efficient and accurate. Second, multi-source data fusion will be another important trend of Bayesian updating in structural damage assessment. Structural damage assessment usually involves multiple data sources, such as monitoring data, sensor data, and historical records. Bayesian updating methods can effectively fuse these multi-source data to provide more comprehensive and accurate structural damage information. With the rapid development of IoT, big data and other technologies, multi-source data fusion will become an important means of structural damage assessment, and Bayesian updating methods will play a greater role in this field.