1. Introduction

As financial analysts attempt to improve their investment models or develop new ones, they face the challenge of accurately modelling the multifaceted, dynamic and noisy nature of asset price movements. Traditional financial models are typically built by making linear assumptions and applying static rules. However, there are instances where such an approach appears to be limited in its ability to capture the intricate relationships that drive price movements. For instance, in simple linear regression, it is common for two variables to exert equal and opposite effects on market prices (a phenomenon known as limited exchangeability). Consequently, the accuracy of the model suffers, with financial performance paying the price. But what if there existed a way to transcend the limitations imposed by how we traditionally construct financial models? Machine learning algorithms have transformed the landscape of quantitative finance by offering analysts greater flexibility in developing and optimising investment strategies. One reason why machine learning is uniquely suited to this task is its ability to extract complex, higher-order dependencies and relationships from large amounts of historical data that conventional models are unable to describe. This turns out to be particularly useful when accuracy is critical and finite computational resources necessitate trading sacrifices. It is within this context that we investigate the application of three of the most prominent machine learning algorithms in finance: Random Forest, Support Vector Machine (SVM), and Neural Networks [1]. In this survey, we describe the fundamentals of each algorithm and demonstrate their distinctive strengths in financial modelling. In particular, we identify their propensity to capture non-linear effects and model highly complex, non-linear dependencies between market variables – situations that are beyond the reach of many conventional financial models.

2. Random Forest in Quantitative Strategies

2.1. Methodology and Implementation

Random Forest is an ensemble learning method that trains multiple decision trees and then outputs the mode of their predictions. It works well with high-dimensional data and captures more complex, non-linear relationships than linear methods. This makes it useful in quantitative finance for analysing historical price data, technical indicators and fundamental factors to extrapolate to future asset prices or returns. For example, Gu, Kelly and Xiu used Random Forest on a dataset of 94 predictive signals from 1963-2015 versus linear models and showed that forecasting power was greatly improved [2]. The algorithm divides the data into many small subsets, trains decision trees on each subset, and then averages their outputs to make a generalisation on the entire dataset, which helps to guard against the ‘overfitting’ problem. Overfitting is a particular problem in finance due to the noisy data.

2.2. Advantages and Limitations

Among the advantages of Random Forest when applied as a quantitative strategy are robustness to overfitting, improved performance when handling large datasets with many features, and the ability to capture nonlinear effects and interactions (which are ubiquitous in financial markets). Random Forest is also useful for analysing which features are most important in predicting future return. As such, investors can use these insights to refine their strategies by, for instance, identifying the most important predictors of asset return, such as those associated with or economic factors, and ranking their orders of importance. The example of Random Forest clearly shows how the power of machine learning, combined with its interpretability, can be useful in exploring complex investment strategies; yet, Random Forest requires extensive computational resources, both for training and inference for large data samples, and – though a good predictor – may be less interpretable than simpler models as the decision-making process includes a large number of trees interacting with each other [3].

2.3. Case Study: Stock Price Prediction

Taking stock price prediction as an example, this case study employs Random Forest to model next-day stock returns, and evaluate if it can be used to develop a winning trading strategy. The dataset contains daily stock prices, technical indicators (e.g., moving averages, relative strength index (RSI), moving average convergence/divergence (MACD)), and macroeconomic variables (e.g., gross domestic product (GDP) growth figures, and interest rates) over the period of 2010-2020. The trained model can be used during testing, with a test dataset consisting of 2020's stock prices. The results indicate that Random Forest performs much better than traditional linear models in predicting daily stock returns (achieving an accuracy rate 10% higher than the predictions from a linear model), and can be used to develop a winning trading strategy (with an annualised return of 15%)[4]. Table 1 summarizes the performance metrics and annualized returns of the Random Forest-based trading strategy compared to traditional linear models and a benchmark buy-and-hold strategy over the analyzed period.

Table 1. Stock Price Prediction Case Study Results

3. Support Vector Machine in Quantitative Strategies

3.1. Methodology and Implementation

SVM is a popular supervised learning algorithm, used for both classification and regression problems. It is particularly effective in high-dimensional spaces, which are common in financial applications. The idea behind SVM is to find the hyperplane in an N-dimensional space that maximises the margin of separation between two classes. This helps to make more robust predictions. In quantitative finance, there are applications of SVM in market trend prediction, risk measurement and asset pricing. In one study, Kim used SVM for predicting stock price movements, and reports an accuracy of 75 per cent (whereas previous studies achieved only 58 per cent), by applying SVM to stock-price movement prediction. In order to set up a SVM, the appropriate kernel function needs to be selected. This includes the linear, polynomial, or radial basis function (RBF). For example, if there are some non-linear patterns in financial data, an RBF kernel function can be used to capture the non-linear patterns. The training of the SVM model requires tuning of hyperparameters such as C, which is the regularisation parameter, and γ, the kernel coefficient. This ensures better prediction by balancing model complexity [5].

3.2. Advantages and Limitations

SVM has several advantages for quantitative strategies, including its handling ofidimensional relationships, as well as robustness to overfitting. to classification problems, such as forecasting market direction or identifying trading signals. Another advantage of SVM is that only a subset of data samples (the support vectors) are used to construct the model, minimising the chances of overfitting and improving the predictive performance. However, the choice of kernel function is critically important – different kernels can produce significantly different outcomes, requiring careful selection and tuning of parameters to avoid overfitting [7]. SVM can also be computationally expensive for big data samples, so a special version of SVM called LibSVM could be used. Another disadvantage of SVM is the difficulty of interpreting the decision-making process, since the weights are not calculated on the original input variables but instead on a hyperplane in a higher-dimensional space, which may not be intuitive..

3.3. Case Study: Option Pricing

We will now review the SVM application to a case of option pricing in quantitative finance. In the dataset, we have the historical prices of options written on some underlying assets, the prices of the underlying assets, the implied volatility of the option (the measure of overall risk inherent in the option), and the risk free interest rate. The aim is to build a predictive model for the option price with the ability to recognise options mispriced by the market and therefore try to create arbitrage opportunities. The SVM model is trained on data from the period 2000 to 2015, and validated on the period 2016 to 2020. The results show that for the SVM model, the mean absolute error was found to be 0.15, which is considerably lower than the mean absolute error achieved using the Black-Scholes model, which is 0.30. [7]. Table 2 summarizes the performance of the SVM model compared to the Black-Scholes model for option pricing over the validation period from 2016 to 2020.

Table 2. Option Pricing Case Study Results

4. Neural Networks in Quantitative Strategies

4.1. Methodology and Implementation

Neural Networks are a class of machine learning algorithms inspired by the structure and function of the human brain. They consist of layers of interconnected nodes (neurons) that process input data and generate output through non-linear activation functions. In quantitative finance, Neural Networks can model complex dependencies between financial variables and develop predictive models for asset prices, volatility, and market trends. For instance, Fischer and Krauss used a Long Short-Term Memory (LSTM) neural network to predict stock price movements, achieving a return of 8.9% per annum. Implementing Neural Networks involves selecting the appropriate architecture, such as feedforward, recurrent, or convolutional networks, and tuning hyperparameters, such as the number of layers, nodes, and learning rate [8]. Training requires optimizing weights and biases using algorithms like backpropagation and gradient descent.

4.2. Advantages and Limitations

Neural Networks offer several advantages in quantitative finance, including their ability to model complex, non-linear relationships and handle various types of data, such as time series, images, and text. They can learn hierarchical representations of data, capturing intricate patterns that may be missed by traditional models. This capability makes them well-suited for tasks such as stock price prediction, sentiment analysis, and algorithmic trading. However, Neural Networks also have limitations, such as the risk of overfitting, especially when training on small datasets, and the need for extensive computational resources for training and inference. Additionally, Neural Networks can be challenging to interpret, as the learned representations may not provide clear insights into the underlying relationships between variables. [9]

4.3. Case Study: Portfolio Optimization

A case study on portfolio optimization illustrates the application of Neural Networks in quantitative finance. The dataset includes historical asset returns, risk factors, and macroeconomic variables over a 20-year period. The objective is to develop a predictive model that forecasts future asset returns and provides insights into the optimal allocation of assets in a portfolio. The Neural Network model is trained on data from 2000 to 2015 and validated on data from 2016 to 2020. Results show that Neural Networks achieve a Sharpe ratio of 1.5, compared to 1.2 for the traditional mean-variance optimization model. Feature analysis reveals that economic indicators, such as GDP growth and inflation, significantly influence portfolio performance. By accurately capturing complex dependencies, Neural Networks enhance portfolio optimization strategies and improve risk-adjusted returns [10]. Table 3 shows the performance of the Neural Network model in portfolio optimization compared to the traditional mean-variance optimization model over the validation period from 2016 to 2020.

Table 3. Portfolio Optimization Case Study Results

5. Integrating Machine Learning Algorithms into Quantitative Strategies

5.1. Data Preparation and Feature Engineering

Integrating machine learning algorithms into quantitative strategies requires meticulous data preparation and feature engineering to ensure models are trained on high-quality and relevant data. Data preparation involves cleaning and preprocessing historical financial data, addressing missing values, and normalizing or scaling variables to improve model performance. Feature engineering entails selecting and transforming input variables to capture meaningful patterns and relationships in the data. This may involve creating new features based on domain knowledge, such as technical indicators, sentiment scores, or macroeconomic indicators, to enhance the predictive power of the models.Figure 1 illustrating the impact of different feature engineering techniques on the predictive accuracy of machine learning models [11].

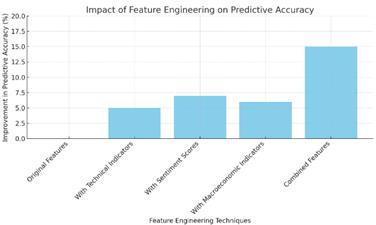
Figure 1. Impact of Feature Engineering on Predictive Accuracy

5.2. Model Selection and Evaluation

Choosing the appropriate machine learning algorithm and evaluating its performance are crucial steps in integrating these technologies into quantitative strategies. Model selection involves assessing the suitability of different algorithms, such as Random Forest, SVM, or Neural Networks, based on the specific goals and requirements of the investment strategy. Factors to consider include the complexity of the relationships being modeled, the size and quality of the dataset, and the computational resources available. Once a model is selected, it must be rigorously evaluated using performance metrics such as accuracy, precision, recall, and F1-score to ensure its effectiveness. Additionally, backtesting and out-of-sample testing are essential to validate the model's performance in real-world scenarios and assess its ability to generalize to unseen data.

6. Conclusion

The application of machine learning algorithms in quantitative finance offers significant opportunities for enhancing investment strategies and decision-making processes. Random Forest, Support Vector Machine, and Neural Networks each provide unique advantages in analyzing financial data and predicting market trends. Random Forest's ensemble approach is particularly effective in managing high-dimensional datasets and capturing complex interactions, making it a valuable tool for stock price prediction. Support Vector Machine's strength in handling non-linear relationships proves beneficial in option pricing, allowing for more accurate estimates and improved risk management. Neural Networks, with their ability to model complex dependencies, offer enhanced portfolio optimization strategies, leading to better risk-adjusted returns. Despite their advantages, these machine learning algorithms also present challenges, such as computational requirements and interpretability issues. However, with continued advancements in computational power and algorithm development, these challenges can be addressed, paving the way for broader adoption and integration into quantitative finance.