1. Introduction

Contrastive learning, as a primary approach within self-supervised learning, is widely applied to feature learning across various data types such as images [1], text [2], and sound [3]. The aim of contrastive learning is to minimize the distance between instances of the same class while maximizing the distance between instances of different classes. The core idea of this approach lies in learning effective feature representations by comparing (contrasting) the similarity and dissimilarity between data samples, as depicted in Figure 1. In contrastive learning, the strategy for sampling positive (similar) and negative (dissimilar) samples is a crucial area of research because it directly impacts the effectiveness and efficiency of the learning process [4]. The choice of which samples to use as positives and negatives profoundly influences the learning objectives and difficulty during optimization. Moreover, in practical applications, sample distributions may exhibit high levels of imbalance and complexity. Therefore, designing effective sampling strategies for selecting positive and negative samples is a significant research challenge aimed at enhancing model learning efficiency and generalization capabilities.

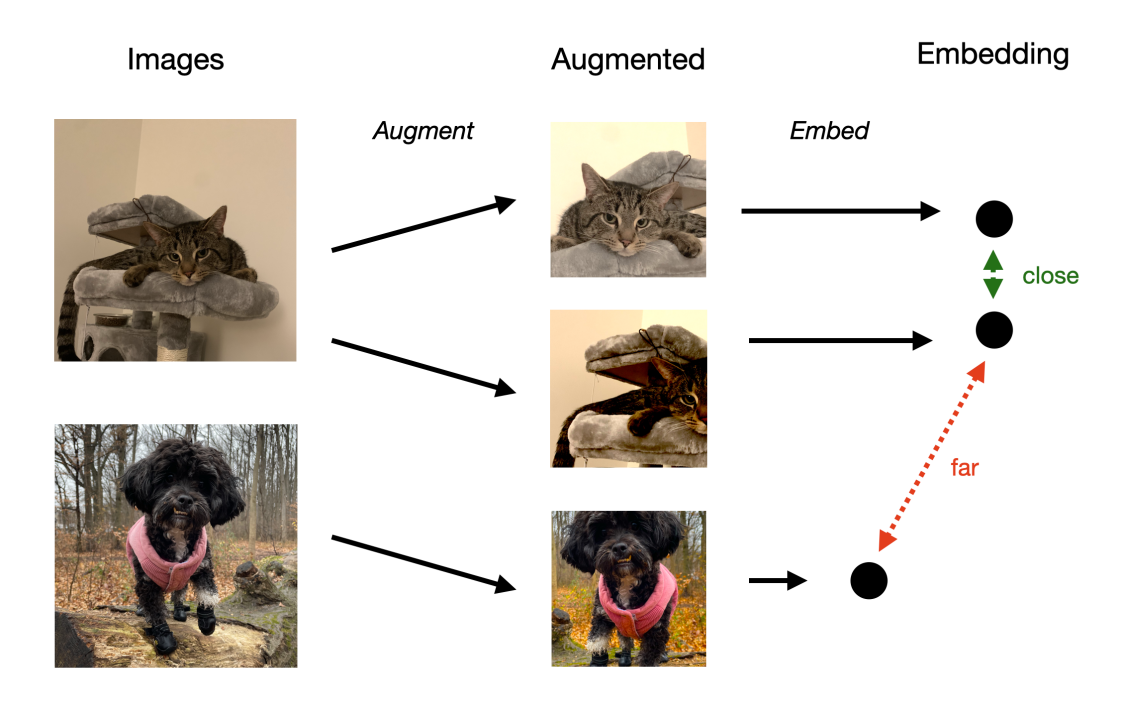
Figure 1. Basic conceptual diagram of contrastive learning.

Research on sampling strategies for positive and negative samples in contrastive learning has been continuously evolving, and as of 2023, significant progress has been made in this field. During the dataset sampling process, several main strategies are currently employed: firstly, random sampling [5], which involves randomly selecting positive and negative samples from the dataset; secondly, hard negative mining [6], which focuses on selecting negative samples that are highly similar to positive samples; and finally, false negative identification strategies [7], which aim to identify negative samples that actually belong to the same semantic category as positive samples using specific methods, and subsequently exclude or treat them as positive samples in contrastive learning. While these methods are effective, they also have their limitations. For instance,

1. Random sampling may lead to uneven sample quality when dealing with imbalanced data distributions, thereby affecting overall learning effectiveness.

2. Overemphasis on hard negative mining can potentially cause model overfitting, and the process of identifying hard negatives incurs additional computational costs.

3. False negatives may lead to misleading learning and degradation of model performance, yet effective criteria for filtering false negatives (and false positives) are currently lacking.

Building upon SimCLR [8], this study innovates by integrating weights pretrained under the DINO framework into the ResNet-50 architecture. Leveraging self-supervised learning on extensive unlabeled data, DINO captures richer and more discriminative visual features. These features serve as the starting point for the SimCLR task, facilitating faster learning and improved generalization of the model. Additionally, we adjusted the similarity matrix of sample pairs by introducing a threshold: similarity scores below this threshold are reduced by 0.5, thereby decreasing the similarity scores between pairs that are already less similar. This adjustment further enlarges the distance between positive and negative sample pairs.

2. Related work

Contrastive learning falls within the realm of self-supervised learning. This learning approach has demonstrated significant development and application potential in various fields such as image recognition [9], natural language processing [10], and sound analysis [11]. The following are some important works related to contrastive learning, each contributing to the advancement of this field.

2.1. SimCLR method

SimCLR, proposed by Google in 2020, is a straightforward yet effective framework for visual contrastive learning, as depicted in Figure 2. Its core idea is to minimize the consistency among different images (negative sample pairs) while maximizing the consistency among similar images (positive sample pairs) to learn feature representations. The specific structure is as follows:

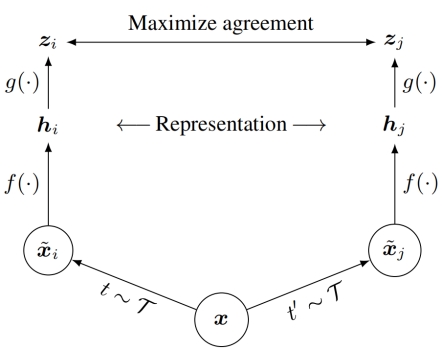
Figure 2. SimCLR framework.

• SimCLR applies two different data augmentation methods to the same image to obtain a pair of positive samples. These augmentations may include random cropping, color distortions, Gaussian blurring, and others. For negative samples, SimCLR utilizes all other images within the current batch; in each batch, besides the positive samples matching a given image, all other images are considered as negative samples.

• SimCLR employs the deep neural network ResNet-50 as an encoder to extract feature representations from images.

• After feature extraction, SimCLR utilizes a small neural network (projection head) to project the features into a lower-dimensional space.

• In this space, contrastive loss computation takes place. The loss function utilized is NT-Xent loss (Normalized Temperature-scaled Cross Entropy Loss) [12]. This type of loss function is particularly suitable for handling a large number of negative samples.

2.2. MoCo method

MoCo [13], proposed by Facebook AI in 2019, is another influential contrastive learning framework, as shown in Figure 3. Its primary contributions include the introduction of a momentum encoder and a dynamic dictionary queue, effectively enhancing the diversity and quantity of negative samples. The specific architecture is detailed as follows:

• MoCo utilizes two encoders: one for the current image (Query Encoder) and another for encoding keys in a dictionary (Key Encoder). The parameters of the Key Encoder are the exponential moving averages of the Query Encoder's parameters, a design that helps maintain consistency in encoding.

• MoCo shares the same positive sample selection strategy as SimCLR, creating positive sample pairs by applying different data augmentation techniques to the same image.

• In contrast to positive sample selection, MoCo innovates in negative sample selection by employing a dynamic dictionary queue to store historical encoded samples as negatives. This queue, of fixed size, retains representations of samples from previous batches. As new samples are encoded, they are appended to the end of the queue, displacing the oldest samples at the front.

• MoCo uses the InfoNCE [14] contrastive loss function to compute the similarity between positive and negative sample pairs.

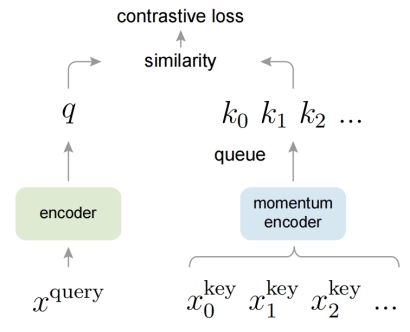
Figure 3. MoCo framework.

2.3. Contrastive Learning with Hard Negative Samples

The paper "Contrastive Learning with Hard Negative Samples" [15] extensively discusses methods and principles of using hard negative samples in contrastive learning. This strategy dynamically selects negative samples close to positive sample features based on the current model state, considering inter-sample similarity (inner product). During the model training process, the selected hard negative samples evolve accordingly. Initially, the model may struggle to differentiate between different samples, hence many negative samples appear "hard". As the model gradually learns more effective feature representations, it becomes capable of accurately identifying genuinely hard negative samples.

2.4. Incremental False Negative Detection for Contrastive Learning

The paper "Incremental False Negative Detection for Contrastive Learning" [16] introduces an incremental method for detecting and identifying false negative samples. This approach gradually removes false negative samples based on their confidence scores, starting from those that are relatively easier to distinguish, thereby mitigating their negative impact on the overall contrastive learning model. As the model performance improves, progressively more challenging false negative samples are excluded to further optimize model performance.

2.5. Other work

The paper "Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning" [17], unlike traditional contrastive learning methods that rely on pairs of negative samples, explores an algorithm that learns without directly utilizing negative sample pairs [18]. It introduces two networks, a target network and an online network, where the online network is trained to predict outputs of the target network without directly employing pairs of negative samples.

"Unsupervised Learning of Visual Features by Contrasting Cluster Assignments" employs a unique approach by contrasting cluster distributions between different views (i.e., augmented versions of data) for contrastive learning. This method allows the model to perform representation learning and clustering simultaneously without directly comparing data samples.

"Supervision Exists Everywhere: A Data Efficient Contrastive Language-Image Pre-training Paradigm" [19] proposes a multimodal contrastive learning model that jointly trains image and text representations on large-scale datasets. By learning correlations between image content and descriptive text, it understands and generates cross-modal content, exhibiting strong generalization capabilities for new tasks.

"Representation Learning with Contrastive Predictive Coding" [20] introduces a contrastive learning approach applied to sequential data. It learns useful representations in sequences by predicting future data representations rather than directly reconstructing data, showing outstanding performance in both audio processing and natural language tasks.

"Prototypical Contrastive Learning of Unsupervised Representations" [21] combines prototypical learning with contrastive learning to enhance learning efficiency and representation quality. This method maps data points onto representations of prototypes (i.e., centroids or representative points of data), particularly beneficial for tasks requiring fine-grained classification or segmentation.

3. Contrastive Learning Method Based on Differential Augmentation

3.1. Research motivation

Current contrastive learning approaches predominantly utilize randomly generated pairs of positive and negative samples [22]. While simple and effective, this approach may lead to inconsistent sample quality when handling complex datasets. Moreover, random generation can result in insufficient differences between positive and negative samples, making it challenging for the model to accurately distinguish between them. The distinctiveness between positive and negative sample pairs is crucial for the model to learn discriminative feature representations effectively in contrastive learning. Nonetheless, SimCLR fails to fully consider the similarity between samples when generating positive and negative sample pairs, resulting in inadequate discriminative power between them.

Addressing these limitations, this study innovates upon SimCLR by proposing a novel method. Leveraging the DINO pre-training model [23], we compute feature similarities and adjust the similarity matrix by reducing elements below a specified threshold by 0.5. This adjustment further enlarges the gap between positive and negative samples, aiding the model in better distinguishing between them. (To facilitate better understanding of this operation, we provide an illustrative adjustment of the similarity matrix as shown in Figure 4.)

Figure 4. Illustrative Adjustment of Similarity Matrix

3.2. Representation Learning Method Based on SimCLR

3.2.1. Conceptual Overview

SimCLR is a popular contrastive learning approach aimed at enhancing model performance in unsupervised or semi-supervised learning by learning feature representations of data samples. The fundamental concept of SimCLR involves applying different data augmentation transformations to the same image to generate multiple views and learning representations by maximizing the similarity between these views. This contrastive learning framework helps the model acquire more accurate feature representations.

3.2.2. Representation Learning Process

Figure 5 illustrates the four main components of this framework.

Figure 5. SimCLR Framework Structure

( \( {z_{i1}} \) , \( {z_{i2}} \) ,……, \( {z_{ik}} \) are negative sample features corresponding to the ith sample)

4. Data Augmentation: This process transforms the same data sample into two correlated views, labeled as \( x_{i}^{1} \) and \( x_{i}^{2} \) , forming a pair of positive samples. The aim is to enhance the training data further by adding diversity to the samples.

5. Feature Extractor: Utilizing the neural network base encoder f (·) (ResNet-50) as the feature extractor, which extracts feature representations from augmented data samples.

6. Projection Head: In neural networks, the function of the projection head g (·) is to project the data representations into a latent space suitable for computing contrastive losses. We apply a hidden layer MLP to obtain \( {z_{i}}=g({h_{i}})={W^{(2)}}σ{(W^{(1)}}{h_{i}}) \) , which introduces non-linear features using ReLU as the activation function.

7. Contrastive Loss Function: This function is designed to increase the similarity between positive samples while decreasing the similarity between negative samples. By comparing the numerator and denominator, the model is constrained to learn relatively. Higher numerator values and lower denominator values indicate that the model successfully captures the associations between positive sample pairs and distinguishes them from other negative pairs. The loss function used in SimCLR is the NT-Xent loss:

\( {l_{i,j}}=-log\frac{exp⁡(sim({z_{i}},{z_{j}})/τ)}{\sum _{k=1}^{2N}{I_{[k≠i]}}exp⁡(sim({z_{i}},{z_{k}})/τ)} \) (1)

3.3. Methodology and Model

3.3.1. Method Overview

We have enhanced SimCLR by proposing a novel contrastive learning approach. In contrast to traditional SimCLR, we employ the DINO pre-training model to compute feature similarity. DINO is a visual Transformer model based on self-supervised learning, renowned for its strong feature extraction capabilities and learning efficiency, applicable across various visual tasks [24]. A key innovation of our method lies in the adjustment of the similarity matrix. In conventional SimCLR, the similarity matrix is solely used to measure the similarity between positive and negative sample pairs. However, we further modify the similarity matrix by applying adjustments specifically to elements with similarity scores below a given threshold, subtracting 0.5 from these scores. This adjustment aims to widen the distance between positive and negative sample pairs, thereby enhancing the model's ability to distinguish between them.

3.3.2. Feature Extraction from Pre-trained Models

In our approach, we utilize the DINO pre-trained model for feature learning by loading its weight parameters into the ResNet-50 network.

In DINO, the model initially learns feature representations from large-scale image data through self-supervised learning. By constructing self-supervised tasks such as image reconstruction and contrastive learning, DINO autonomously learns statistical structures and semantic information within image data without requiring manual annotation. Experimental results demonstrate its outstanding performance across various visual tasks. Compared to traditional CNN models [25], DINO maintains lower computational costs while offering more discriminative and generalizable feature representations, thus providing a stronger foundation for solving diverse visual tasks.

We incorporate the weights of the DINO pre-trained model into the ResNet-50 architecture of SimCLR. Through this integration, we apply the rich feature representations learned by DINO within the contrastive learning framework of SimCLR, thereby enhancing the model's performance in tasks such as image classification.

3.3.3. Enhancement of Contrastive Sample Diversity

We introduced the Enlarge Distance operation on top of the original SimCLR model, which adjusts the similarity matrix to increase the distance between positive and negative samples. Specifically, we penalize similarity scores below a predefined threshold (subtracting a fixed value of 0.5). This adjustment effectively enlarges the gap between positive and negative samples, thereby enhancing the model's capability to differentiate between these two types of samples. This method focuses primarily on more challenging sample pairs, thereby improving the robustness and applicability of the model.

In Figure 6, we illustrate the distribution of sample similarity scores before and after the adjustment of the similarity matrix. Prior to adjustment, similarity scores exhibited a basic normal distribution, with most scores clustering around intermediate values and fewer scores concentrated near extreme values. This distribution pattern could lead the model to excessively prioritize sample pairs with high similarity scores, neglecting crucial information from other pairs.

The change in distribution pattern following the adjustment reflects distinctive characteristics of the adjusted similarity matrix. Compared to the pre-adjustment normal distribution, the post-adjustment distribution tends to favor lower similarity scores, indicating that the model now focuses more on challenging sample pairs, while penalizing pairs with higher similarity scores to some extent. This adjustment aims to facilitate better learning of discriminative and generalizable feature representations, thereby enhancing the model's performance across various visual tasks.

In summary, by carefully designing and adjusting penalty mechanisms, we can guide the model towards learning more discriminative and generalizable feature representations. This improvement strategy is not only applicable to traditional contrastive learning methods but can also be integrated with other self-supervised learning frameworks [26], offering novel approaches and methods for model training and feature learning.

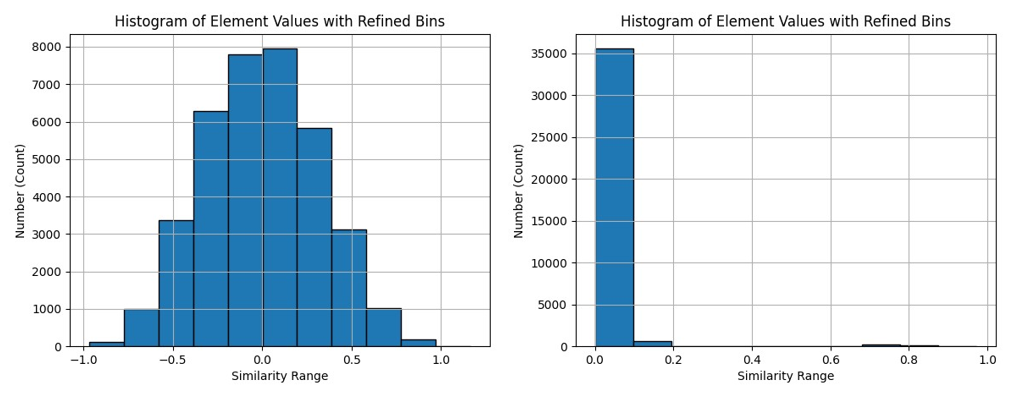
Figure 6. Distribution of Similarity Scores

(The left image shows the pre-adjustment scenario, while the right image shows the post-adjustment scenario. After normalizing the feature vectors in the right image, the range of similarity scores becomes [0,1].)

3.3.4. Learning Process Representation

This paper innovatively improves upon the SimCLR framework by optimizing aspects such as feature extractor and contrastive loss function. The following are the main four components of our model framework, as illustrated in Figure 7.

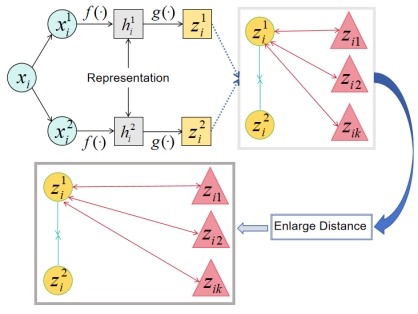
Figure 7. The improved model framework

( \( {z_{i1}} \) , \( {z_{i2}} \) ,……, \( {z_{ik}} \) are negative sample features corresponding to the ith sample)

8. Data Augmentation: [27] Here, we employ a variety of data augmentation techniques, including random cropping, color distortion, and Gaussian blur. The purpose of these augmentation operations is to generate two positively correlated views, enabling the model to learn the essence of image content rather than relying excessively on specific visual details.

9. Feature Extractor: The feature extractor [28] is a core component of the model responsible for extracting meaningful feature representations from input data. We opted for the ResNet-50 backbone encoder. To enhance the model's representational power, we initialized it with weights pre-trained on the DINO framework. This initialization imbues the base encoder's features with enhanced discriminative capability.

10. Projection Head: The projection head is a crucial component that maps feature representations into the contrastive loss space. Here, we employ an MLP with one hidden layer as the projection head, utilizing ReLU as the activation function for the hidden layer. This design enhances the model's non-linear capacity, thereby enriching and distinguishing the feature representations more effectively.

11. Contrastive Loss Function: In our enhancement, we introduced an Enlarge Distance operation that adjusts the similarity matrix across all pairs of samples. Specifically, we subtract 0.5 from similarity scores below a given threshold, thereby reducing the similarity scores of pairs that are not inherently similar, thereby enlarging the distance between positive and negative sample pairs. This operation helps to increase the distinctiveness between positive and negative pairs, enhancing the model's discriminative ability. Our loss function is defined as follows:

\( {l_{i,j}}=-log\frac{exp⁡(sim \prime ({z_{i}},{z_{j}})/τ)}{\sum _{k=1}^{2N}{I_{[k≠i]}}exp⁡(sim \prime ({z_{i}},{z_{k}})/τ)} \) (2)

Our designed loss function numerator reflects the similarity of positive sample pairs, measured exponentially to maximize consistency among target samples. The denominator encompasses the sum of similarities for all sample pairs, covering both positive and other pairs. This design enables us to maximize the distinction between positive and negative sample pairs by comparing the similarity of positive pairs relative to all other pairs.

3.4. Experimental Results

3.4.1. Experimental Dataset

We conducted experiments on the CIFAR-10 and CIFAR-100 benchmark datasets to validate our approach. These datasets are widely used in evaluating and comparing the performance of various machine learning and deep learning models for image classification tasks.

3.4.2. Experimental Setup

Our model was validated for the task of image recognition and classification, which is a fundamental task in the field of computer vision aimed at assigning input images to predefined categories. Specifically, we conducted detailed evaluations of the improved model through two aspects: Fine-tuning and Linear evaluation.

3.4.3. Implementation Details

12. Model Structure: In our study, for feature extraction, we employed ResNet-50 and has been initialized with weights from the DINO pre-training model. Additionally, we utilized an MLP structure with a single hidden layer as a projection head to map high-dimensional features extracted from the feature extractor to a lower-dimensional representation space. ReLU was used as the activation function [29] to enhance the network's representational capacity.

13. MLP Structure: The MLP (Multi-Layer Perceptron) [30] structure serves as the projection head to map high-dimensional features to a lower-dimensional representation space. This MLP structure consists of only one hidden layer.

14. Optimization Method: We employed the LARS optimizer, LARS (Layer-wise Adaptive Rate Scaling) [31], designed to address issues of gradient stability and convergence in deep neural network training.

15. Experimental Settings: The learning rate (LR) was set to 0.001; weight decay was set to 1e-5; batch size was 96; and the number of iterations was set to 200 epochs.

16. Evaluation Metrics: The evaluation metrics included Top-1 and Top-5 classification accuracies.

3.4.4. Experimental Results and Analysis

We extensively validated the improved model on CIFAR-10 and CIFAR-100 datasets, conducting detailed performance analysis. We will systematically delve into our experimental results, including performance enhancements across various tasks and datasets, as well as the advantages of the improved model relative to competitors. Our initial focus will be on the experimental results obtained on the CIFAR-10 dataset.

Table 1. Comparison of Experimental Results on the CIFAR-10 Dataset.

Through Table 1, it is evident that our model has achieved significant performance improvements in both Linear evaluation and Fine-tuned settings on the CIFAR-10 dataset. In Linear evaluation, our model achieved Top-1 and Top-5 classification accuracies of 64.06% and 78.13%, respectively. This represents relative improvements of 3.37% and 3.46%, demonstrating the effectiveness of our enhanced methods in feature extraction and classification tasks. Compared to MoCo, our model has also been significantly improved.

In Fine-tuned evaluation, our model achieved Top-1 and Top-5 classification accuracies of 82.81% and 88.61%, respectively. Compared to SimCLR, our model showed improvements of 7.81% and 10.41% in Top-1 accuracy and relative improvements of 6.36% and 7.73% in Top-5 accuracy. In comparison with MoCo, our model exhibited increases of 5.65% in Top-1 accuracy and 1.69% in Top-5 accuracy, with relative improvements of 7.32% and 1.94%, respectively. These results indicate that our enhanced model adapts better to new data in Fine-tuned scenarios, demonstrating improved generalization ability. As depicted in Figure 8, the Top-1 accuracy and loss function graphs on the CIFAR-10 dataset illustrate these findings.

By contrasting the Top-1 accuracy and loss function graphs in Figure 8, we can visually observe the performance gains of the improved model relative to SimCLR. Experimental results indicate slight enhancements in both loss function and classification accuracy due to our refined methodologies.

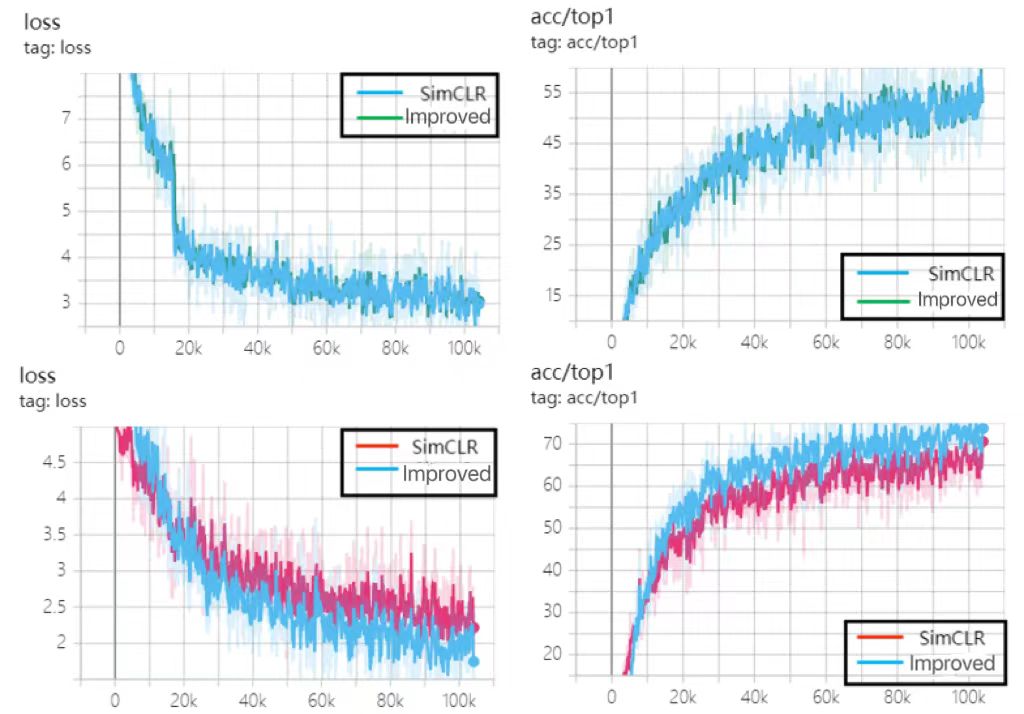
Figure 8. Training Results on the CIFAR-10 Dataset

(where the first row includes the loss curve and top-1 classification accuracy curve for Linear evaluation; the second row includes the loss curve and top-1 classification accuracy curve for Fine-tuned evaluation).

Next, we present our experimental results on the CIFAR-100 dataset.

Table 2. Comparison of Experimental Results on the CIFAR-100 Dataset.

From Table 2, it is evident that our improved approach exhibits substantial performance gains on the CIFAR-100 dataset. In Linear evaluation, our model achieved Top-1 and Top-5 classification accuracies of 59.9% and 75.37%, respectively, marking improvements of 7.82% and 4.14% compared to the SimCLR model. Compared to MoCO, our model showed increases of 0.53% and 7.03% in Top-1 and Top-5 classification accuracies, respectively, further confirming the superiority of our approach across different datasets.

In Fine-tuned evaluation, our model exhibited improvements of 7.29% and 3.63% in Top-1 accuracy compared to SimCLR and MoCo, respectively. For Top-5 accuracy, the improvements were 6.78% and 2.6% over SimCLR and MoCo, respectively. These results underscore the significant advantages of our enhanced model in adapting to diverse datasets and tasks. As depicted in Figure 9, the Top-1 classification curve and loss curve on the CIFAR-100 dataset further validate our model's performance gains.

Figure 9. Training Results on the CIFAR-100 Dataset

(where the first row includes the loss curve and top-1 classification accuracy curve for Linear evaluation; the second row includes the loss curve and top-1 classification accuracy curve for Fine-tuned evaluation).

3.4.5. Ablation experiments

We conducted a series of ablation experiments on our improved method, focusing primarily on validating the effectiveness of the enhancement modules and threshold ablation experiments. Our improvements primarily involve loading the pre-trained DINO model and adjusting the similarity matrix. Below, we detail the results of our effectiveness validation experiments.

Validation Experiments of Improvement Modules:

We designed a series of experiments to evaluate the impact of two enhancements on model performance: whether to load the DINO pre-trained model and whether to adjust the similarity matrix. We employed a range of experimental conditions labeled as T/F, F/T, and T/T, where T indicates loading and F indicates not loading. These combinations covered all possible scenarios, comprehensively assessing the contribution of each enhancement to model performance. As shown in Table 3 below, F/F denotes the original SimCLR model, T/F indicates loading only the DINO pre-trained model, F/T indicates adjusting only the similarity matrix, and T/T indicates both loading the DINO pre-trained model and adjusting the similarity matrix.

Table 3. Validation of Enhancement Modules

From the experimental results in Table 3, it is evident that two enhancements, loading the DINO pre-trained model and adjusting the similarity matrix, significantly impact model performance. Firstly, we focused on the influence of the DINO pre-trained model on model performance. By comparing experimental conditions T/F and F/F, it can be observed that solely loading the DINO pre-trained model without adjusting the similarity matrix improved the Top-1 and Top-5 classification accuracies by 3.64% and 2.14%, respectively. This indicates that loading the DINO pre-trained model markedly enhances the model's feature representation capabilities, thereby improving its ability to learn from data and generalize.

Secondly, we investigated whether adjusting the similarity matrix affects model performance. By contrasting experimental conditions F/T and F/F, we found that solely adjusting the similarity matrix without loading the DINO pre-trained model increased the Top-1 and Top-5 classification accuracies by 2.08% and 1.63%, respectively. This suggests that adjusting the similarity matrix effectively enhances the clustering performance of the model in the feature space, improves similarity measurements between features, and consequently enhances classification performance.

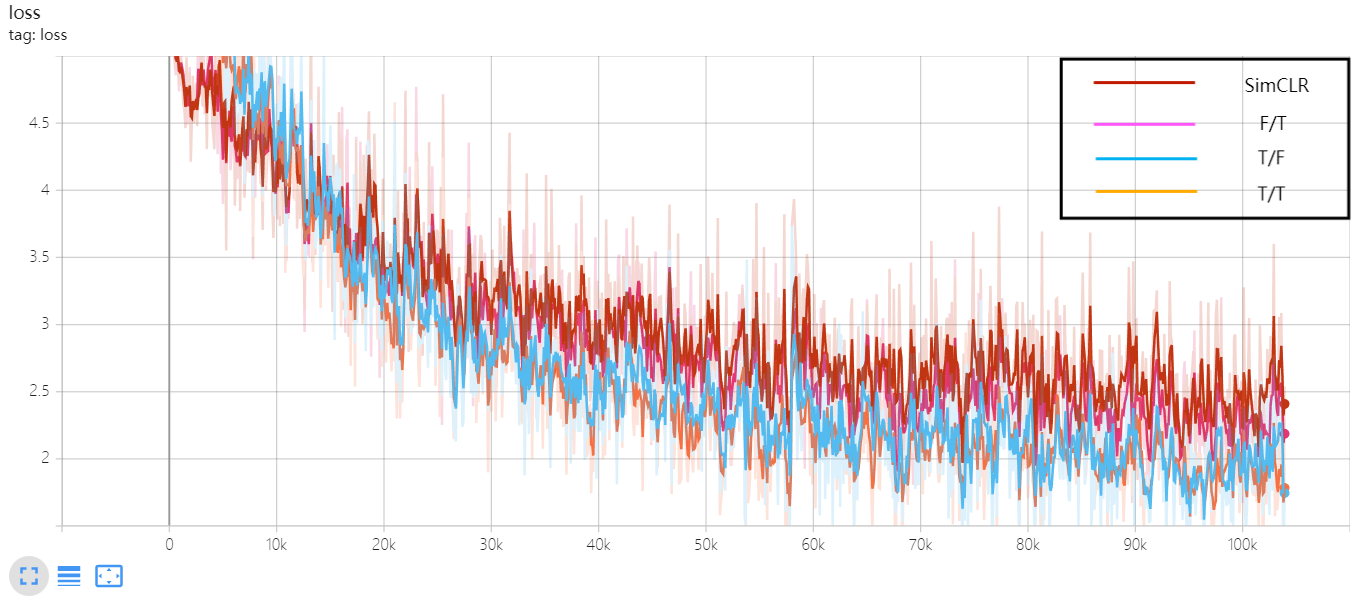
Figure 10. The loss curve of the validation experiment for the enhancement module.

Lastly, we comprehensively assessed the combined effects of loading the DINO pre-trained model and adjusting the similarity matrix. By comparing experimental conditions T/T and F/F, it is evident that when both loading the DINO pre-trained model and adjusting the similarity matrix simultaneously, the model improved its Top-1 and Top-5 classification accuracies by 7.81% and 3.19%, respectively. This further confirms that the combined effect of these two enhancements is more significant than their individual applications alone, contributing significantly to enhancing model performance.

Figure 11. The Top-1 classification accuracy curve of the validation experiment for the enhancement module.

We visualized the experimental results in Figure 10 and Figure 11, which include the loss curve and Top-1 classification curve from the validation experiments of the enhancement modules respectively. Through these plots, we can visually observe the variation in model performance under different experimental conditions, further validating the reliability and effectiveness of our experimental results.

Threshold ablation experiment:

To validate whether model performance is influenced by varying threshold conditions, we conducted threshold ablation experiments. Table 4 below presents the experimental results under different threshold conditions.

Table 4. Threshold ablation experiment

Based on the experimental results shown in Table 4, we conducted an analysis of the variation in model performance under different threshold conditions. Across these experiments, we observed that setting the threshold to 0.75 yielded the optimal performance, with the model achieving a Top-1 classification accuracy of 82.81% and a Top-5 classification accuracy of 88.61%.

The results of the threshold ablation experiments indicate that selecting appropriate thresholds during adjustment of the similarity matrix can significantly impact model performance.

4. Conclusion and Outlook

4.1. Conclusion

This study undertook a targeted exploration in the field of image classification by integrating the weights of the DINO pre-trained model into the SimCLR framework and adjusting the similarity matrix to enhance the model's learning representation and generalization capabilities. This innovative adjustment mechanism provided crucial support for enhancing the performance of contrastive learning methods.

Experimental validation on CIFAR-10 and CIFAR-100 demonstrated significant performance improvements in both Fine-tuning and Linear evaluation methods. These results indicate that our proposed method shows potential in enhancing learning representation quality and efficiency, while paving the way for new perspectives and approaches in future exploration and practice.

4.2. Outlook

The innovative approach proposed in this study provides new insights into the application of contrastive learning in image classification tasks. Moving forward, we aim to further explore the following directions to enhance model performance and application value:

17. Continued Optimization of Model Architecture:

• Investigate the impact of different network depths, widths, and activation functions on model performance.

• Explore lightweight models to accommodate edge computing devices, enabling the model to operate in resource-constrained environments.

18. Enhancement of Positive Pair Generation Methods:

• Explore alternative strategies for generating positive sample pairs, such as using Generative Adversarial Networks (GANs) to obtain more diverse positive samples.

• Experiment with multi-strategy fusion approaches, such as simultaneously employing data augmentation and generative models to create more challenging positive sample pairs.

19. Exploration of Novel Evaluation Metrics and Datasets:

• Develop new evaluation metrics tailored to contrastive learning to comprehensively measure various aspects of model performance.

• Gather and construct more diverse and challenging datasets, particularly addressing issues like few-shot learning and imbalanced class problems, to test and enhance the model's performance limits.

Acknowledgments

I would like to express my gratitude to Professor Zengjie Song for his guidance in conducting the experiments, and to my classmate Siqi Hao for her encouragement and support.