1. Introduction

1.1. Background on greedy algorithms

Algorithms in computer science are the building blocks of effective problem-solving strategies [1]. Greedy algorithms belong to the most basic algorithmic categories that utilize the “greedy strategies” concept, whereby a problem is solved by choosing localized optimal decisions in the hope that the overall optimal solution will be realized. The base idea corresponds to the choice of the optimal decision at each stage to gradually build up the overall best solution [1]. Albeit allowing for simplicity, greedy algorithms originate from combinatorial optimization and theoretical computer science discussions that occurred numerous decades ago [2]. They originated from the need to find solutions on how to solve difficult computational problems as noticed across various fields of application. When problem structures meet certain conditions to guarantee optimality, like optimal subproblems and greedy choice facilities, the greedy algorithms provide well-defined procedural frameworks for solving optimization challenges with optimality in the simplest ways [1]. However, it is essential to mention the shortcomings because greedy heuristics are not always able to provide the optimal solutions and may, at times, stop at a suboptimal solution because subsequent decisions regarding further optimization depend on the previous decisions in some classes of problems [2].

1.2. The widespread use of greedy algorithms

Greedy algorithms have been widely applied to both traditional and modern computational sciences. For instance, in graph theory, greedy algorithms are used to address issues such as MST with Kruskal’s or Prim’s algorithms and the Shortest Path problem with Dijkstra’s algorithm [3]. In addition to this, greedy algorithms have been featured in solving resource allocation problems like the Fractional Knapsack Problem, solving the Activity Selection Problem, and data compression techniques like Huffman Coding to allow for storage space reduction [4]. These application areas demonstrate how the greedy algorithms are useful and meritorious in various domains. It could be argued that greedy algorithms do not always ensure globally optimal solutions regardless of the problem kind, but if the certain problem’s structure can be decomposed into a sequence of admissible greedy choices, then such algorithms will yield an optimal and efficient solution [5].

2. The basis of greedy algorithms

2.1. The core thoughts of greedy algorithms

The greedy algorithm follows the general idea of climbing a mountain, step by step, getting higher and higher with every radical change. In other words, it seeks to find the best solution iteratively [6]. This proves to be a conceptually simple but limited means of handling optimization challenges. Earl’s greedy algorithms do not specify adherence to any particular structure and are solely based on the selection of the “greedy strategy” [6]. This strategy must possess one of the characteristics called “no retrospect” that means that the state after a particular state has no influence on the states before it. From the standpoint of the present state, this decision is unrelated to further consequences. According to [6], greedy algorithms are considered the most basic and fastest approach that could provide optimal solutions to some outlined problems. In particular cases, finding the global optimum comes down to making a number of locally optimal decisions or so-called “myopic strategies” [7]. However, it is important to realize that a neighborhood optimum does not ensure that we get the globally optimal solution. Still, it often helps in deriving an estimative optimal solution [7]. As is the case with the greedy algorithm, every phase just looks at the current best choice for the algorithm, instead of asking whether this choice will be good in the future.

This form of step-by-step optimization constitutes the basis of the functional concept of greedy algorithms. Despite providing conceptual convenience and computational flexibility, their design does not guarantee derivation of categorically best solutions for all types of problems. The selection technique limits inspection to present states that exclude the possibility of reconfiguring prior states, which in turn limits the reach of the optimal solutions guarantee to certain types of problems. Nevertheless, the accumulation of successively locally optimal decisions based solely on the current system state presents the greedy method as capable of providing approximatively optimal or precisely optimal solutions to well-defined optimization problems at a computational complexity that cannot be equaled by exhaustive assessment. This justifies their endurance as one of the basic types of algorithms.

2.2. Mathematical proof

As with other algorithms, the effectiveness of the greedy algorithms can be proven mathematically under certain conditions. This we shall illustrate using the Activity Selection Problem, whereby the aim is to select the maximum number of non-overlapping activities within a given period of time. Every activity has its own start and finish time. A greedy strategy could imply that the chosen activity be the one with the earliest completion time each time a decision was to be made.

2.2.1. Proof. Here, A = {a1, a2, …, an}, represent set of “n” numbers of activity having start time si and end time fi. A greedy algorithm schedules activities by:

• Sort the elements in the set A in non-decreasing order of fi

• And inserting each of the elements with the next element of the same type (ai, ai+1) into schedule S if si ≥ fi [1]

Let P(n) be the proposition stating that for any set of activities, the greedy algorithm yields an optimal ASP schedule. We apply induction in order to prove that P(n) holds for all n.

2.2.2. Base case: In case n = 1, it is quite obvious that this single activity will schedule optimally. P (1) is true.

Inductive hypothesis: Suppose that P(k-1) is true for some k-1 activities.

2.2.3. Inductive step: Let there be a set of activities A, where |A| = k If the greedy algorithm is such that the first activity chosen is a1 then A’ = A - {a1}. By the inductive hypothesis, the greedy algorithm optimally schedules A’. The union schedule of activity a1 and all activities in A’ is optimal since none of the A’ activities coincide with all.

Therefore, for every n in the set of natural numbers N, (∀n ∈ N,) P(n) statement is valid based on the principle of mathematical induction. Q.E.D.

The successful proof given in this paper utilizes mathematical induction to show that the greedy algorithm given above is capable of arriving at an optimal schedule in the context of the ASP [1]. Let P(n) = Greedy approach gives an optimal schedule for any activities on n. The base case is established for =1, because there will only be activity scheduled and this will be done optimally. Therefore, for the inductive hypothesis, we assume that P (k - 1) is true for k-1 activities. In the inductive step, a set A of k activities is taken into account. For simplicity, let A’ represent the set of activities after the first activity (a1) to be scheduled greedily is deleted. Therefore, the greedy activity can be seen as indicated in Table 1 below. By the inductive hypothesis of the greedy method, the above schedule of node A’ is the optimum schedule. As a result of completing logical induction, the hypothesis P(n) holds for any natural number n, meaning that the greedy selection in nondecreasing order of finish times and insertion of pairs where start exceeds prior finish will provide the best solution to the ASP. This is due to the inherent characteristic of the selection strategy to build the best solution from some starting point step by step by choosing the best local solution at each step. While this guarantee can only be proven mathematically in specific and limited circumstances, they do assure that the best overall arrangement will be recognized, which is what the A* algorithm is primarily designed to do [1,2].

Table 1. Activity Schedule Validation.

Greedy schedule: a3, a1, a5

3. The logic of greedy algorithms

3.1. Advantages and disadvantages of greedy algorithms

Greedy algorithms have some advantages that imply the simplicity and high performance of these algorithms. Their iterative, gradual strategy that leads to the global optimization by approximating local optimization at each stage makes sense in a quite heuristic way [6]. This simple nature facilitates its ease of understanding, implementation, debugging and modification, thus giving shorter development times than may be expected when using more complex algorithms [6]. Moreover, greedy methods usually indicate splendid time complexity when problem characteristics are rightly matched to a one-pass, myopic choice mechanism [8]. Since they do not keep track of the preceding calculations, greedy algorithms require the smallest amount of memory and can solve vast problem instances with basic computing technology within acceptable time frames. Their efficiency thus allows for the analysis of the large resource-intensive datasets, which might be cumbersome to other methods [8]. It is vitally important to remember that greedy algorithms do not guarantee the categorically best solution for all problems and still, they deliver outcomes that are near optimal – the solutions that are reasonably implementable, specifically in the case of computationally intensive problems [8]. This makes them suitable for a wide spectrum of practical optimization problems where nearly-optimal solution times, or rates of convergence, are much more important than actual identification of global optima.

However, there are also some drawbacks to using greedy algorithms as well. Their successive decisions get reduced to functions of selection process and problem definition only. If these do not align with requisite features like optimal substructures and the greedy-choice principle, greedy algorithms stand to produce results that are highly sub-optimal or inefficient [10]. Consequently, Figure 1 shows Comparison of Greedy Algorithms with Other Optimization Techniques in details. In addition, lack of forward planning prevents one from identifying if early choices are still perfectly appropriate as the issue unfolds. Greedy algorithms do so at the expense of heuristically scanning the whole solution space at every selection point for the sake of computational efficiency. Though performing very well on particular classes of problems, greedy heuristics require good knowledge of related drawbacks for determining harmony with target tasks.

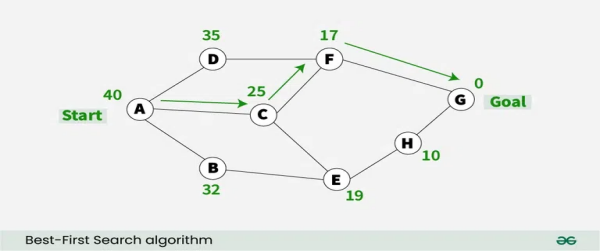
Figure 1. Comparison of Greedy Algorithms with Other Optimization Techniques.

Chart comparing the time complexity of greedy algorithms, dynamic programming, and backtracking

Figure 2. Example of a Greedy Algorithm Applied to the Fractional Knapsack Problem.

Flowchart depicting the stages in the greedy approach for the fractional knapsack problem (Figure 2). Combining the information presented above, it can be stated that greedy algorithms provide an effective instrument in solving optimization problems. It is important to state that these structures are easy to design, effective in their performance and useful in approximating solutions to an array of problems.

3.2. Examples of greedy algorithms in action

In order to give a more detailed description of greedy algorithms, two problems, which are Fractional Knapsack and Shortest Path, are explained below. The Fractional Knapsack Problem involves selecting the largest value containing item set getting into a knapsack of restricted weight; here, every item has a unique weight and value [11]. In a greedy approach, an ‘‘item is chosen from which has the highest value-divided-by-weight at each step with due consideration of weight’s constraints. Although optimality is not ensured, this approach assembles incrementally the best solution within minimal deviation relative to the optimum based on locally efficient decisions. The Shortest Path Problem involves computing the least number of edges between two nodes in an edge-weighted graph [12]. Iterative graph exploration is achieved by a greedy algorithmic approach; Dijkstra’s selection at each step is the unvisited node with the smallest total distance from the source node. Upon reaching the destination, the reconstructed path represents the shortest path to travel. Both exhibit greedy algorithms that work by making steps of pure choices of the best local improvements to achieve approximate global optimal solutions. At each step, focusing exclusively on the present utility of those systems provides people with decisions that are not influenced by the future. Although it is not possible for greedy algorithms to assert categorically that other solutions are non-optimal, the factors of time efficiency, approximation of optimal solutions and proven optimal solutions for certain types of problems uphold the general applicability of greedy algorithms. What concerns their properties, these structures are especially appropriate for large-scale computationally oriented problems where slight imperfection is acceptable to achieve near optimal solutions. Exactly, greedy algorithms suitably solve problems with characteristics such as optimal substructures and the greed choice property. Despite such shortcomings, a general aim of simple solutions tends to overshadow the concomitant sub-optimality associated with these algorithms to qualify the greedy approach as a brute-force method of first choice.

4. Applications of greedy algorithms in the real world

Greedy algorithms have vast applicability in real-life scenarios. The distribution tasks that involve rationed resources that have to be distributed among several competing needs are usually performed using greedy strategies. Other examples are CPU scheduling, mentioned before, and bandwidth management in networks, in which near-optimal schedules are built by choosing the highest priority allocation over and over again [13]. Greedy optimization is used rather pervasively in real-life applications; for example, data compression. One of the most basic compression methods is Huffman coding, which generates efficient prefix codes for symbols in relation to the frequency by a greedy algorithm. Chronologically assigning short codewords to frequent symbols reduces the overall storage space needed [14]. Machine learning algorithms also appear with greedy thinking incorporated into their systems. The classification technique of decision tree learning continually picks the attribute in each loop that creates the “purest” divisions of subgroups and goes on subdividing the observations in that way until their conclusion or end branches in a prediction. This greedy construction of optimal splitting decisions constructs decision trees step by step and therefore improves interpretability [15]. These are to illustrate how greedy algorithms may be applied to various aspects of resource storage and retrieval, and information sorting and assessment. The efficiency of their methods and reasonable solutions derived from iterative improvement of solutions within local optima allow for solving many problematic issues of optimization maintenance in computationally intensive practical applications. When a global optimum cannot be determined, greedy algorithms’ blend of strong throughput with decent solution quality allows for a wide range of application areas for system management, for example [13-15]. Due to their practical, straightforward, and efficient characteristics, these are some of the most useful techniques for simulating optimization problems in technology, science, and other fields where optimal solutions may not necessarily be necessary on a global scale.

5. Conclusion

Some techniques, such as the greedy algorithms, have become firmly rooted in the field of computer science because of the demonstrated ability of generating solutions that are approximations of the optimal values rapidly. These basic advantages stem from the simplicity of ideas that underlie them, time requirements, and the ability to iteratively choose the locally optimum decision. Even though greedy heuristics do not always provide global optimality, they are used because they always provide reasonable, approximate or optimal solution. This makes it possible to solve very large problem instances intractable to thin, more general exhaustive approaches. When the problems belong to well-defined categories that can be mapped to greedy principles, we know that better solutions are guaranteed to bolster this strategy’s effectiveness. However, increasing compatibility with greedy algorithm properties, such as optimal substructure and the greedy choice property improves the solution. Moreover, an awareness of limitations and biases that originate from myopic vision is crucial for determining relevance and assessing its applicability as well as guarding against possible sub-optima. However, overall structural simplicity usually makes up for occasional sub-optimal solutions, thus supporting greed-based methods as first choices. Flexibility occurs from leverage throughout resource management, information processing, analytical processing, among others. It’s an essence aimed at a pragmatic approach at optimizing the quality of solutions and the speed of how they are delivered bridging the gap between the mere technicality of investigation and the specific scientific pursuit of an answer. Subsequently, the perpetual identification of more suitable problem domains reinvigorates the theoretical basis of greedy algorithms. As problems grow with technology, efficient approximate methods require more need as the scale increases. The long-term relevance of greedy algorithms can therefore be safely assumed. Despite the optimization potential of stochastic variants, the sheer concept and computation ease that stochastic methods afford underline their eternal uses in optimization.