1 Introduction

Techniques for path planning and obstacle avoidance have significant potential for application in a variety of areas, including autonomous driving, unmanned aerial vehicle (UAV) control, and industrial robotics. However, the development of effective and dependable path planning and obstacle avoidance techniques in complex and evolving environments represents a significant and ongoing challenge. This study aims to address the challenges posed by dynamic and unpredictable environments, whereas traditional methods often fall short in terms of adaptability and efficiency [1][2]. In this paper, the efficacy of algorithms for efficient path planning and obstacle avoidance in dynamic environments is explored by comparing the traditional Q-Learning method and the optimized Double DQN method. Through the experimental analysis, the advantages of the optimized model in complex dynamic environments are verified. Specifically, this study indicates that the performance of robotic systems in real applications can be significantly improved by combining heuristic strategies with advanced reinforcement learning techniques. Therefore, the paper presents the design of two experimental systems: the initial model and the optimization model. The initial model employs the fundamental Q-Learning method, whereas the optimization model integrates the dual DQN algorithm and heuristic policies. The performance advantages and disadvantages of the two models are assessed through a comparison of their training and testing outcomes in an identical environment. The research adheres to a meticulous experimental design to ensure that the results are statistically significant and reproducible. Furthermore, the research is conducted in a MATLAB environment, leveraging the Reinforcement Learning Toolbox to implement and train the models.

2 Literature Review

Techniques for path planning and obstacle avoidance are important topics in mobile robot research. These technologies are critical for the autonomous operation of robots, enabling them to navigate through complex environments without human intervention. In recent years, the development of deep learning technology has led to a growing interest in the application of deep reinforcement learning in path planning and obstacle avoidance. Traditional methods, such as A* algorithm and Dijkstra’s algorithm, despite their effectiveness in static environments, often struggle with dynamic changes and require extensive computational resources [3][4]. In contrast, deep reinforcement learning optimizes path selection strategies through interaction with the environment, with advantages such as strong adaptability and high learning efficiency. Reinforcement learning allows agents to learn optimal behaviors through trial and error, leveraging rewards and penalties to guide their decisions. Common methods in path planning and obstacle avoidance include DQN, Double DQN, and their variants, which have shown promise in addressing the limitations of traditional approaches [5][6]. Heuristic strategies combine the advantages of traditional path planning methods, thus effectively improving the learning efficiency and the path planning effect of the model by guiding the learning process. The combination of domain-specific knowledge and heuristic strategies allows for a significant reduction in the search space and an increase in convergence speed. This approach is particularly advantageous in complex environments where purely data-driven methods may necessitate extensive training to attain satisfactory performance [7][8].

3 Methodology

3.1 Experimental System Design

The experimental system consists of an initial model, which adopts the basic Q-Learning approach, and an optimized model, which combines a Double DQN algorithm and a heuristic strategy, as shown in Figure 1. Both models are implemented in the MATLAB environment, leveraging the capabilities of the Reinforcement Learning Toolbox for algorithm development, training, and evaluation. The Reinforcement Learning Toolbox in MATLAB provides a comprehensive array of features, including model training, debugging, and performance assessment, so as to facilitate the development and optimization of intricate reinforcement learning algorithms. As a result, this design allows for a systematic comparison of the traditional Q-Learning approach with the advanced method integrating Double DQN and heuristic strategies. Furthermore, it evaluates their performance in a variety of environments in terms of learning efficiency, strategy optimization, and adaptability to environmental changes..

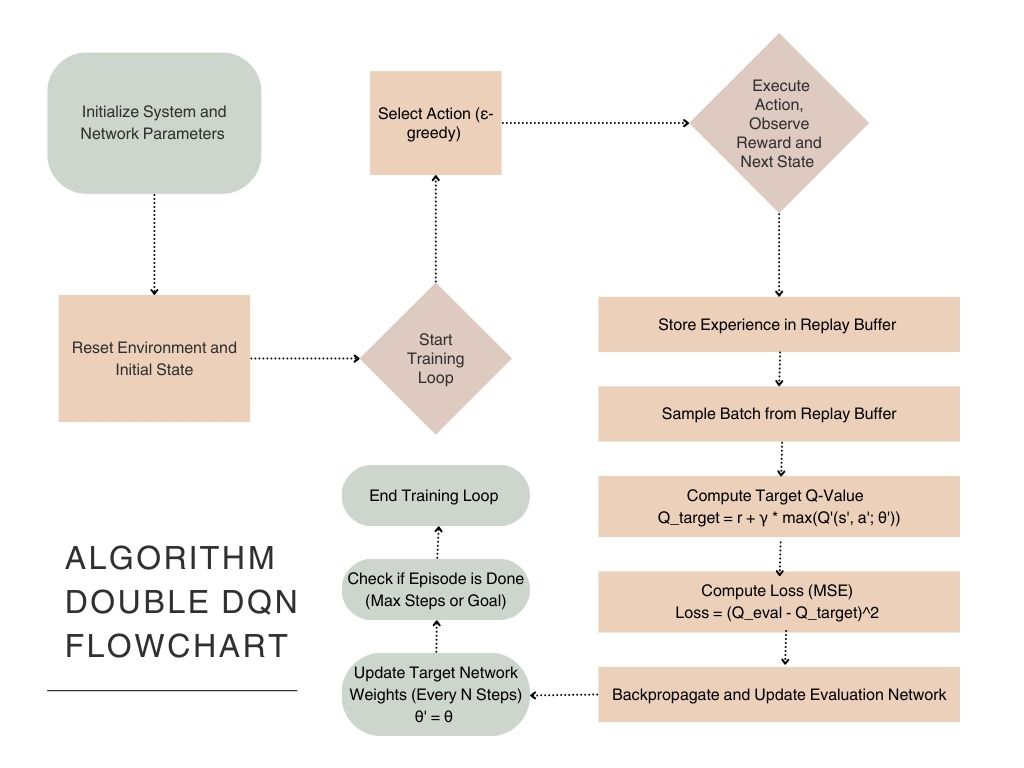
Figure 1. Algorithm Double DQN Flowchart

3.2 Initial Model Design

The core algorithms of the initial model include state update and reward calculation, as shown in Eqs. (1) and (2):

robotPosotion \( =\begin{cases}robotPosition+[0,1] (up) \\ robotPosition+[0,-1] (down) \\ robotPosition+[-1,0] (left) \\ robotPosition+[1,0] (right)\end{cases} \) (1)

which is used to update the current state of the robot so that it can adjust its decision-making strategy based on feedback from the environment.

\( reward=-∥robotPosition-goalPosition∥-10∙I(distanceToObstacle \lt 1) \) (2)

which is used to compute the reward after the robot takes action in a given state. Negative rewards are used to penalize the robot for having a collision or taking a sub-optimal path, thus guiding the robot to learn to avoid these unfavorable situations.

This basic models enables robots to progressively optimize their behavioral strategies through reinforcement learning mechanisms. However, due to the simplification of its approach, the initial model may be limited in its ability to navigate when faced with complex, dynamic environments. This limitation is mainly reflected in its weak ability to adapt to changes in complex environments, as well as the lack of an effective strategy to quickly find the optimal path when encountering multiple possible path choices. Consequently, while the fundamental model offers a foundation for learning, more sophisticated techniques may be necessary to enhance performance and adaptability in practical applications.

3.3 Optimized Model Design

The optimized model is an extension of the initial model, incorporating the Double DQN algorithm and heuristic strategies, as shown in Eqs. (3) and (4):

\( guidedQValues=α∙heuristicCost+(1-α)∙qValues \) (3)

\( reward=-∥robotPosition-goalPosition∥-10∙I(distanceToObstacle \lt 1)-0.1∙(|robotPosition\text\lbrace _\rbrace 1-goalPosition\text\lbrace _\rbrace 1|+|robotPosition\text\lbrace _\rbrace 2-goalPosition\text\lbrace _\rbrace 2|) \) (4)

The reward function in the optimized model is further refined by the addition of a penalty for path smoothness, which encourages the robot to choose routes that are not only efficient but also safer. Specifically, the model addresses potential problems such as path discontinuities and obstacle interference by incorporating smoothness criteria into the reward structure. In this way, the robot is able to evaluate and optimize its decision-making strategy more comprehensively, thereby improving navigation and safety. The optimization model aims to better handle dynamic environments, improve decision accuracy and action efficiency, thereby reducing risk and uncertainty and enhancing robot performance in complex tasks.

4 Experimental Results and Analysis

4.1 Initial Model Results Analysis

The average reward during the training of the initial model is -2268.9165, which indicates its poor performance in path planning and obstacle avoidance. The training curve shows that the initial model exhibits significant fluctuations in the early stages of training and stabilized later, but with low reward values, indicating limited performance improvement. This result highlights the inherent limitations of basic Q-learning in handling dynamic and unpredictable environments. The training parameters of the initial model are shown in Table 1, and the training curve of the initial model is shown in Figure 2.

Table 1. The Relevant Training Details and Parameters of the Initial Model

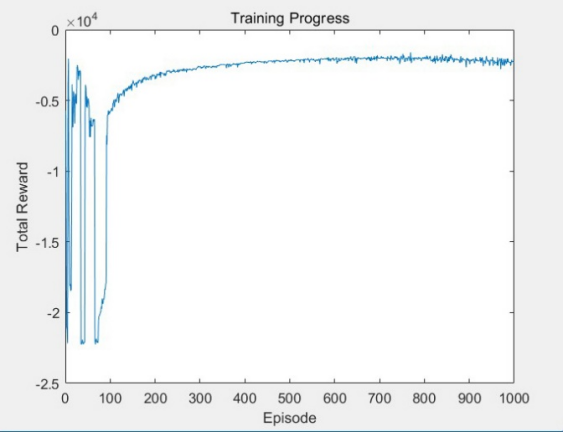
Figure 2. The training curve of the initial model

4.2 Optimized Model Results Analysis

The average reward during the training of the optimized model is -1580.5414, significantly higher than the initial model. The training curve shows that the optimized model also fluctuates significantly at the beginning of the training period, but the reward value gradually increases and stabilizes at the later stage, demonstrating better path planning and obstacle avoidance performance. These improvements underscore the effectiveness of combining Double DQN with heuristic strategies in enhancing the learning and decision-making processes of the robot. The training parameters of the optimized model are shown in Table 2, and the training curve of the optimized model is shown in Figure 3.

Table 2. The relevant training details and parameters of the optimized model.

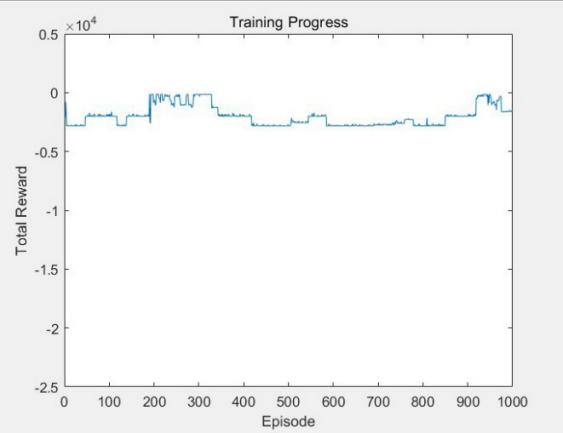
Figure 3. The Training Curve of the Optimized Model

Figure 4 shows a comparison between the training curve of the initial model and the training curve of the optimized model:

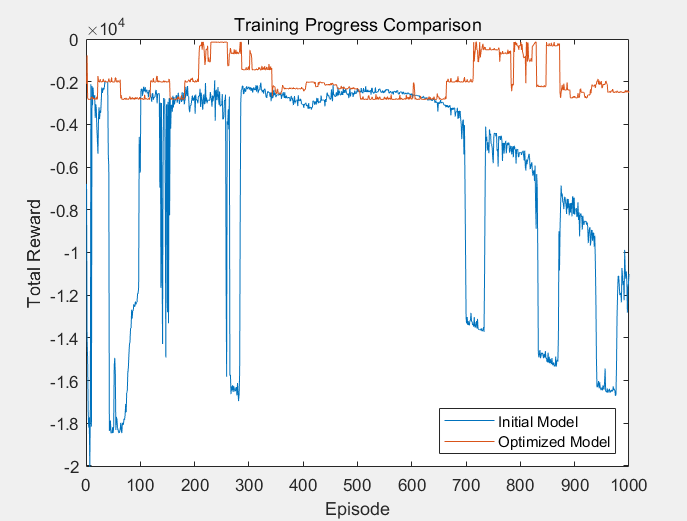
Figure 4. Comparison of the Training Curves between the Initial Model and the Optimized Model

The optimized model consistently outperforms the initial model in terms of total reward throughout the training process. The initial model shows significant fluctuations and instability, with frequent drops in reward, indicating inefficient learning and poor performance. In contrast, the optimized model maintains a relatively stable and higher total reward from the early stages of training, indicating that the optimization has significantly improved the model's learning efficiency and overall performance.

5 Discussion

5.1 Advantages of the Optimized Model

The optimized model demonstrably enhances learning efficiency and path planning performance through the incorporation of the Double DQN algorithm and heuristic strategies. The Double DQN algorithm enhances learning outcomes by differentiating between the target Q-value and the current Q-value, thereby mitigating the potential for Q-value overestimation. This separation facilitates the stabilization of the learning process, thereby enabling the implementation of more reliable policy updates [9][10]. The incorporation of heuristic strategies enhances the rationality and stability of path planning, enabling the robot to make more informed decisions based on both learned experiences and pre-defined heuristics [1][11]. This approach employs domain-specific knowledge to furnish auxiliary guidance throughout the training process, enabling the model to circumvent suboptimal pathways and concentrate on more promising regions of the solution space. As previously stated, the integration of heuristics with deep reinforcement learning results in the development of a more robust and efficient path planning algorithm.

5.2 Core Algorithms of Model Optimization

The core algorithms of the optimized model encompass state update, reward calculation, and Q-value estimation. By meticulously accounting for path smoothness and obstacle proximity, the optimized model can effectively plan routes and avoid obstacles in complex dynamic environments [12][13]. As mentioned above, the state update formulation, which describes how the robot’s position changes with different actions, is the basis of the state transition function, which ensures that the robot updates its position based on discrete actions, facilitating the learning of the optimal motion strategy. Regarding reward calculation, the initial model employs a reward function that primarily considers the robot's distance to the goal and collisions with obstacles. This function uses negative distance and penalty terms to guide the robot in avoiding obstacles and approaching the goal. While this simple reward function is easy to implement, it may not capture all nuances of a dynamic environment. In contrast, the optimized model introduces an enhanced reward function that includes a path smoothness penalty, which encourages the robot to choose more reasonable paths, minimizing unnecessary turns and detours. The improved reward function not only considers goal distance and obstacle avoidance but promotes smoother paths, which is crucial for real-world applications where abrupt movements can lead to inefficiencies or safety hazards. For Q-value estimation, the Double DQN algorithm employs Equation (5) that reduces the risk of Q-value overestimation by separating the target Q-value from the current Q-value, improves the robustness of the model in dynamic environments, and stabilizes the learning process, especially in environments with large and complex state and reward spaces.

\( Q_{(s,a;θ)}=r+γmax^{ \\prime a}Q_{(s^{ \\prime },a^{ \\prime };θ^{ \\prime })} \) (5)

Furthermore, the integration of heuristic strategies into Q-value adjustment enhances the model’s performance. By combining heuristic insights with the learned Q-values, the model benefits from both empirical data and domain-specific guidance. This dual approach improves learning efficiency and path planning, ensuring a more effective and comprehensive decision-making process.

5.3 Implementation in MATLAB

The experimental setup and model implementation are performed in MATLAB with the functionality of the Reinforcement Learning Toolbox that provides robust support for developing and evaluating reinforcement learning algorithms, including predefined functions and environments that simplify the design, training, and deployment of agents. The environment was set up using MATLAB’s custom functions to simulate a dynamic scenario with moving obstacles. The state space included the robot's position and the positions of obstacles, while the action space consisted of discrete movements such as up, down, left, and right. This design introduces a high degree of complexity and dynamism to the environment, which is crucial for assessing the model's performance under realistic conditions. For agent configuration, the Double DQN agent utilizes two neural networks, one for policy evaluation and another for target Q-value estimation, to improve Q-value accuracy and model stability. These networks are trained using backpropagation with mean squared error as the loss function to ensure precise Q-value estimation. In the training process, the agent learns through multiple interactions with the environment, employing an experience replay mechanism to store and sample past experiences. This approach not only increased the diversity of learning data but also reduced overfitting to recent observations, thereby enhancing the model’s learning efficiency and decision-making quality.

5.4 Verification of Experimental Results

The experimental results show that the optimized model performs significantly better than the initial model in terms of average reward and more stable learning curves in path planning and obstacle avoidance tasks, which verifies the effectiveness and robustness of the optimized model in dynamic environments. Figures 2, 3, and 4, along with Tables 1 and 2, provide a detailed comparison of the algorithm's performance before and after optimization. These visual and tabular representations clearly illustrate how the optimized model enhances performance. Specifically, the training curves of the initial model highlight its limited performance and high variability, which often led to inconsistent results and sub-optimal performance. In contrast, the optimized model displays more consistent and gradual improvements over time, achieving higher average reward values. The enhanced stability and performance of the optimized model can be attributed to the integration of heuristic strategies and advanced reinforcement learning techniques. By incorporating heuristic guidance, the model benefits from domain-specific insights, which complement the data-driven learning approach of Double DQN, leading to more efficient path planning and more reliable obstacle avoidance, thereby improving the overall capabilities of the robotic system. These results highlight the significant advantages of employing sophisticated reinforcement learning techniques and heuristics to not only improve the efficiency and effectiveness of robotic systems, but also to ensure their reliability when dealing with complex and changing environments, underscoring the immense benefits of model optimization.

6 Conclusion

This study explored the development and optimization of algorithms for robot path planning and obstacle avoidance in dynamic environments. By comparing a traditional Q-learning approach with an advanced model that integrates Double Deep Q-learning (Double DQN) and heuristic strategies, the research demonstrates potential improvements in both efficiency and reliability. The optimized model generally performed better than the initial model across various metrics, particularly in addressing the challenges posed by dynamic and unpredictable environments. The deployment of the Double DQN algorithm was effective in reducing the overestimation bias commonly seen in Q-Learning, leading to more stable and accurate policy decisions. Furthermore, the inclusion of heuristic strategies provided additional guidance, which enhanced the model’s ability to navigate complex scenarios and improve the learning process. Overall, this research highlights the potential benefits of advanced reinforcement learning techniques in developing robotic systems capable of real-time decision-making in dynamic settings. The findings provide useful insights that can inform the design of more efficient and reliable algorithms for future applications in autonomous systems, robotics, and related fields.