1. Introduction

The ability to generate realistic images has significant implications across various fields, including art, entertainment, healthcare, and autonomous systems. In recent years, Generative Adversarial Networks (GANs) have revolutionized the domain of image generation [1,2]. GANs consist of two competing neural networks: a discriminator and a generator. The role of the generator is to fabricate data that emulates a specified dataset, whereas the discriminator's objective is to discern genuine data from the fabricated data. These networks participate in a minimax competition where the generator endeavors to fool the discriminator, and the discriminator strives to precisely differentiate between authentic and counterfeit data. This dynamic has enabled GANs to produce highly realistic images, significantly advancing the field of image synthesis. The traditional GAN framework, while groundbreaking, has several limitations that have prompted the development of various GAN variants. One of the prominent challenges associated with GANs is the lack of stability during the training phase, often caused by the use of the Jensen-Shannon (J-S) divergence to measure the difference between real and generated data distributions. When the discriminator becomes too strong, it can lead to vanishing gradients, making it difficult for the generator to improve. Additionally, conventional GANs encounter problems like mode collapse, wherein the generator yields a restricted range of variations in the synthetic images, thereby undermining the diversity of the generated output. [3,4].

To address these challenges, Wasserstein GANs (WGANs) were introduced by Arjovsky, Chintala, and Bottou in 2017 [5]. WGANs utilize the Wasserstein distance, also known as the Earth-Mover distance, which are designed to quantify the smallest expense required to shift mass in order to convert one distribution into another. This distance provides a more meaningful measure of distribution similarity, leading to improved training stability and addressing some of the shortcomings of traditional GANs. Despite these improvements, WGANs face their own set of challenges, particularly with weight clipping, which can either slow down the training process or lead to vanishing gradients, especially in deeper networks [6].

To overcome the limitations of weight clipping in WGANs, researchers updated the WGAN with Gradient Penalty (WGAN-GP). This modification substitutes the previous weight clipping approach with a gradient penalty mechanism, which enforces a Lipschitz condition by ensuring that the gradient magnitude of the critic's response to its input remains approximately one. The gradient penalty not only contributes to the stabilization of the training phase but also improves the quality of the produced images, rendering the WGAN-GP a more resilient and potent framework for tasks involving image synthesis [6].

This work will discuss the implementation and analysis of WGAN-GP. This approach integrates the core principles of WGAN with gradient penalty and applies them to the CIFAR-10 dataset, a widely recognized benchmark for image generation tasks. By leveraging the code, which incorporates techniques like batch normalization and adaptive optimizers, this work aims to demonstrate the improvements in training stability and image quality achieved by WGAN-GP. Furthermore, this work explores the effects of various hyperparameters, such as the learning rate, gradient penalty coefficient, and critic iterations numbers per generator update, providing insights into the optimization of WGAN-GP for different image generation scenarios.

2. Method

2.1. Principle of WGAN

WGAN represents a significant advancement over conventional GANs, which suffers from issues like training instability and mode collapse [5]. In traditional GANs, the generator sometimes produces limited and repetitive outputs due to difficulties in the training process. WGAN addresses these challenges by using the Wasserstein distance, which offers more consistent and significant gradients throughout the training process. This results in a more stable learning process and boosts the generator's capacity to generate a variety of high-fidelity images. The WGAN framework is also less sensitive to the specific architecture of the network and hyperparameter settings, making it easier to train across different datasets and conditions [5,7].

WGAN begins with the initialization of two neural networks: the generator, aim at creating synthetic data, and the critic, which replaces the discriminator used in traditional GANs. The objective is to assess the similarity between the generated data and the actual data. The system processes a set of authentic data samples as input, and concurrently, the generator creates a set of artificial data by converting random noise vectors, which are drawn from a specified distribution. The critic is subsequently trained to punish the discrepancy between its evaluations of the real data and the synthetic data. This process involves several iterations of updating the critic’s parameters. A crucial aspect of WGAN is the enforcement of the Lipschitz constraint on the critic, which is done by clipping the weights of the critic network to a fixed range after each iteration. This clipping ensures that the critic operates within the space of 1-Lipschitz functions, which is necessary for the Wasserstein distance to update correctly after each iteration. After the critic has been updated, the generator is trained to improve its outputs based on the feedback range from the critic. The generator's goal is to generate data that the critic will deem as genuine, thereby minimizing the Wasserstein metric between the actual and synthetic data distributions. Unlike traditional GANs, where two modules are trained simultaneously, WGAN trains the critic more frequently than the generator. This allows the critic to approach optimality, providing more accurate gradients for the generator's updates. Then after iterations and iterations, the output will be better and better [5,8].

2.2. Principle of gradient penalty

Although WGAN improves upon traditional GANs, its reliance on weight clipping to enforce certain constraints introduces new challenges, such as slow training and potential gradient vanishing issues in deeper networks. To address these drawbacks, Gulrajani et al. proposed WGAN-GP in 2017 [6]. Rather than employing weight clipping, WGAN-GP utilizes a gradient penalty to impose the required constraints more efficiently and avoids the adverse impacts associated with weight clipping. WGAN-GP retains the core principles of WGAN but replaces weight clipping with the gradient penalty, which more effectively evaluating the Lipschitz constraint on the critic network. Instead of using weight clipping to evaluate critic to lie within a fixed range, WGAN-GP imposes a penalty on the magnitude of the critic's gradient relative to its input. This ensures that the gradient magnitude stays near one, upholding the Lipschitz condition while circumventing the drawbacks of weight clipping.

This gradient penalty is computed with a interpolate parameter between real and generated data samples which start from 0 (entire generated data) to 1 (entire real data), then determining the magnitude of the gradient of the critic's output concerning these interpolated instances. Though critic’s loss is will be larger because of the gradient coefficient, but this approach not only stabilizes the training process but also allows for more effective training of the critic, even in deeper networks.

The gradient penalty stabilizes the training process, allowing WGAN-GP to train faster and produce higher-quality images. This approach also makes WGAN-GP more stable and effective across different types of datasets and tasks.

This work aimed to demonstrate the advantages of WGAN-GP over the standard WGAN by applying both models to well-known datasets, such as CIFAR-10 and MNIST.

It concentrated on refining critical elements of the training regimen, encompassing the learning rate, the frequency of critic updates for each generator iteration, and the coefficient for the gradient penalty. After examination, the learning rate performance best between 0.0001-0.00005 and the gradient penalty coefficient should between 5 and 15.

By meticulously adjusting these parameters, this research managed to enhance the training process's efficiency and attain superior image quality. The experiments clearly showed that WGAN-GP consistently outperformed the standard WGAN, especially at the beginning phase of the learning, by producing clearer and more distinct images. This work also explored the impact of different blocking strategies and hyperparameters on the results, confirming that the gradient penalty significantly enhances both the speed of convergence and the overall quality of the generated images.

3. Result

3.1. Dataset

For experiments, this work utilized two widely recognized datasets: CIFAR-10 and MNIST. CIFAR-10 comprises 60,000 color images, each measuring 32x32 pixels, spanning 10 distinct categories, and is frequently utilized for the training of image processing algorithms. [9]. The MNIST dataset consists of 70,000 grayscale images of handwritten digits (0-9) in 28x28 pixel format [10]. These datasets provide a robust foundation for evaluating the performance of generative models like WGAN and WGAN-GP.

3.2. Performance comparison

The experiments were conducted over 20 iterations, comparing the performance of WGAN and WGAN-GP at intervals of 5, 10, and 20 iterations. Key hyperparameters were carefully selected for fair comparison between the two models. They were trained using the same architectures for the generator and critic, with identical batch sizes, learning rates, and optimizer configurations. The only difference in training was the incorporation of the gradient penalty in WGAN-GP. Images were generated and saved at each interval to visually compare the progression and quality of the generated outputs.

The comparison between WGAN and WGAN-GP across different iterations reveals distinct differences in image quality and clarity.

Generated images of CIFAR-10 dataset, at 5, 10, 20 iterations are respectively demonstrated in Figure 1, Figure 2, and Figure 3. At the beginning phase of learning, WGAN-GP produced images that were significantly clearer and more distinct compared to those generated by standard WGAN. The images generated by WGAN appeared blurred and lacked defined boundaries, whereas the WGAN-GP images had clearer shapes. After 10 iterations, WGAN still struggled with color distribution and clarity, often producing predominantly green images. In contrast, WGAN-GP generated more colorful and well-defined images, demonstrating better overall performance. By the 20th iteration, both WGAN and WGAN-GP produced relatively clear images, though WGAN-GP still maintained a slight edge in terms of image quality and distinction.

Figure 1. Generated images of CIFAR-10 dataset at 5 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

Figure 2. Generated images of CIFAR-10 dataset at 10 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

Figure 3. Generated images of CIFAR-10 dataset at 20 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

Generated images of MNIST dataset, at 5, 10, 20 iterations are respectively demonstrated in Figure 4, Figure 5, and Figure 6. WGAN-GP started producing recognizable digit shapes as early as the 5th iteration, while WGAN’s outputs were still blurry and undefined. By the 10th iteration, WGAN-GP continued to show more recognizable digits, with sharper edges and clearer shapes than those generated by WGAN. At 20 iterations, both models produced similar quality outputs, though WGAN-GP had consistently shown faster convergence to clear and distinct image generation throughout the earlier iterations.

Figure 4. Generated images of MNIST dataset at 5 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

Figure 5. Generated images of MNIST dataset at 10 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

Figure 6. Generated images of MNIST dataset at 20 training iterations by WGAN and WGAN-GP (Figure Credits: Original).

These comparisons clearly show that WGAN-GP consistently outperforms WGAN in terms of training speed and image quality, particularly at the early phase of learning. This aligns with the findings of Gulrajani et al., who demonstrated that the inclusion of gradient penalty accelerates convergence and produces images with high quality.

In addition to comparing WGAN and WGAN-GP, this study also investigated how different gradient penalty influence the quality of the generated images. This analysis was conducted by comparing the Inception Scores across different iterations, as illustrated in Figure 7. Specifically, the figure shows how adjusting these parameters, with a learning rate of 0.0001, batch size of 64, and gradient penalty coefficient of 10, impacted the clarity and distinctness of the images produced by both WGAN and WGAN-GP.

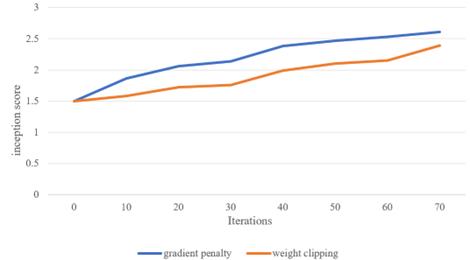
Figure 7. Comparison between WGAN and WGAN-GP (Figure Credits: Original).

4. Conclusion

In a nutshell, this work explored the effectiveness of WGAN and its improved variant, WGAN-GP, this method applies gradient penalty instead of clipping weight which could leads to unstable and inefficient problem, the results demonstrated that WGAN-GP consistently outperformed the standard WGAN, particularly at the beginning phase of training, by producing clearer and more distinct images. The gradient penalty not only enhanced training stability but also accelerated convergence, confirming its superiority in image generation tasks. This method has proved its potential for broader applications in generative tasks where image quality and training efficiency, Future work could explore further optimizations, such as adaptive gradient penalty or integration with other advanced techniques such as sound generating.