1. Introduction

Regulating building materials to optimize internal climate conditions and reduce energy consumption is crucial in modern architecture, particularly in cold climates where focused solar heat is essential during winter. Glass, a common material in contemporary buildings, plays a central role in this optimization process as it facilitates the transfer of solar energy into interior spaces. Improving thermal conditions within buildings can be achieved by adjusting glass composition or applying multiple glass layers. However, recent advancements in numerical analysis offer new possibilities for varying the thickness of glass layers to achieve desired thermal characteristics. The ability to fine-tune these layers to enhance indoor solar heat gain is particularly important in cold northern regions, where maintaining warmth while reducing energy usage is a significant challenge [1].

The transmission of solar energy through multiple layers of glass is well-documented in the literature, with established mathematical equations describing the basic concepts of light transmission and reflection at interfaces between different media [2]. Previous studies have demonstrated that the thickness of glass layers directly influences the amount of solar energy that penetrates indoor spaces, thus impacting both thermal comfort and the energy required for heating [3]. However, most existing research has focused on single and double-layer glass configurations, with limited exploration of the potential benefits of multi-layer systems optimized through advanced algorithms. Notably, one study employed a genetic algorithm (GA) to optimize the thickness of multilayered glass for various climates, proving the method's effectiveness in enhancing the Solar Heat Gain Coefficient (SHGC) in cold regions [4]. However, GA’s limitations, such as the complexity of crossover and mutation operations, can lead to suboptimal solutions. In contrast, the Ant Colony Optimization (ACO) algorithm, with its iterative pheromone trail updating mechanism, shows promise in finding more optimal solutions for complex optimization problems like glass thickness configuration.

Research Content: This study aims to address the research gap by investigating the application of the Ant Colony Optimization (ACO) algorithm to optimize the thickness of multilayer glass for maximizing solar heat gain in buildings located in cold climates. The research focuses on using ACO to adjust the thicknesses of three glass layers to enhance thermal comfort and reduce energy consumption. ACO’s ability to handle complex, multi-modal optimization problems makes it an ideal candidate for this task. Additionally, the study incorporates wavelength-specific optimization into the ACO framework, recognizing that solar energy transmission varies with wavelength, and different glass configurations yield different results depending on the specific wavelengths involved [5]. By integrating these considerations, the research seeks to provide a more sophisticated approach to optimizing glass thickness for maximum solar energy transmission. The findings are expected to contribute significantly to the sustainable design of buildings, offering practical solutions for architects and engineers aiming to improve indoor heat comfort in cold climate regions through advanced optimization techniques [6].

2. Methodology

This research seeks to determine the right t values for three layers of glass; L1, L2 and L3 for maximum conversion of solar energy into an indoor environment using Ant Colony Optimization (ACO) algorithm. The methodology involves several key steps: deriving the constraints for the objective function formulation, choosing and determining the parameters for ACO, calculating the intensity of the light passing through the glass layers and using ACO to determine the best glass thicknesses for the design [7].

The first thing that has to be said about the optimization process is the definition of the objective function which is one of the key aspects of the process. The objective function in this present study is the overall energy transmittance through the three layers of glass and is formulated as total solar transmittance energy in the wavelength range of 3000-2000 nm. Transmitted energy by a glass is determined by the optical transmittance given by the refractive index of glass, the thickness of every layer and the wavelengths of the incident light. The transmittance formula is given by \( T=\frac{\left(1 - R\right)^2}{\left(1 - R\right)^2+4R\left(sin\left(\delta\right)\right)^2} \) ,where R is the reflection coefficient and \( \delta \) is the phase delay caused by the glass thickness. These equations are integrated over the wavelength range to calculate the total transmitted energy. This was earlier determined as the objectives are in the equations above function to be maximize.

Next, the ACO algorithm is configured with appropriate parameters to ensure efficient and accurate optimization.

As show in the figure 1. The ACO algorithm itself is set to mimic the behavior of ants while looking for food or sources of food. Every ant corresponds to a solution, or to a precise configuration of the glass thicknesses (L1, L2, L3). Based on the trail intensity and the heuristic values of ants, the ants probabilistically choose their path and the heuristic value in this work was found to be inversely proportional to the wavelength. When the ants migrate to the solution space they adjust the trails in accordance to the quality of the solution they come across [8].

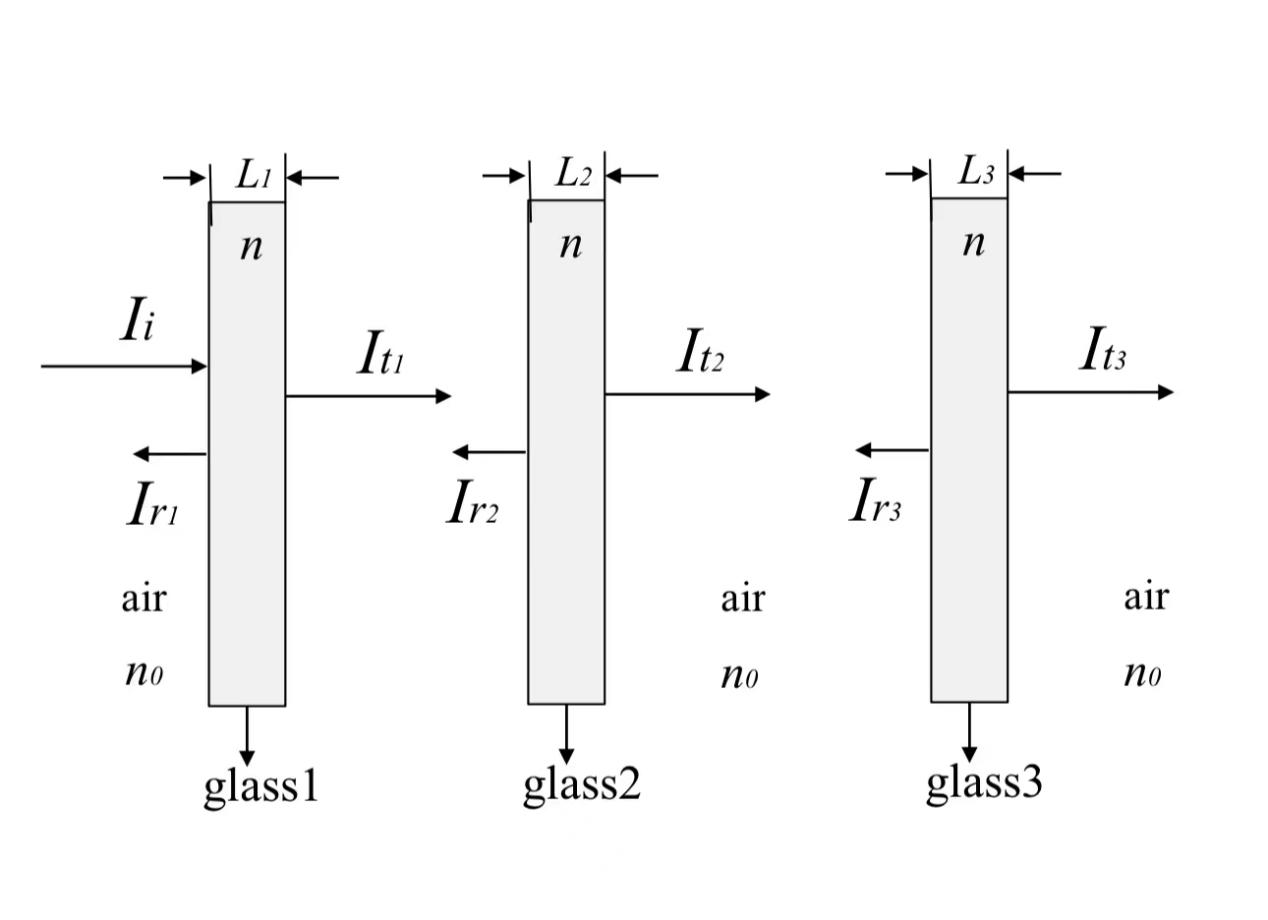
Figure 1. Structure diagram (Photo credit: Original).

Even though the model of the constructive now incorporates three layers, the optimization process starts with each ant choosing randomly thicknesses of the layers. The energy transmitted to each set of thickness value can then be determined using the objective function identified, above. After all ants have completed their paths the pheremone levels are updated and the algorithm moves to the next iteration. In each run through of the algorithm, it gets closer to the values of thickness that allow for maximum transmission of the solar energy. The resulting thicknesses for the glass layers are the optimum thicknesses achieved by the ants in the process of optimization [9].

Lastly, the obtained results are evaluated in order to determine the efficiency of the ACO algorithm in determination of the thickness of the glasses. The solidity of the solution is assessed based on the comparison of the optimized glass layers under various environing conditions and lighting spectra. The work also embodies a proper applicative case of the algorithm under a real-world context, showing its usefulness to solve other optimization problems in engineering and design.

3. Results

The Ant Colony Optimization (ACO) algorithm that was proposed was able to find the optimal thickness values for the three layers of glass L1, L2 and L3 that provide the greatest transmission of solar energy to indoors. The optimal thicknesses determined by the algorithm are as follows: The current results obtained were alarmingly low thus L1 = 5.9289 mm, L2 = 7.9309 mm, L3 = 3.8462 mm, Maximum Transmission= 0.81258. As show in the figure 2.

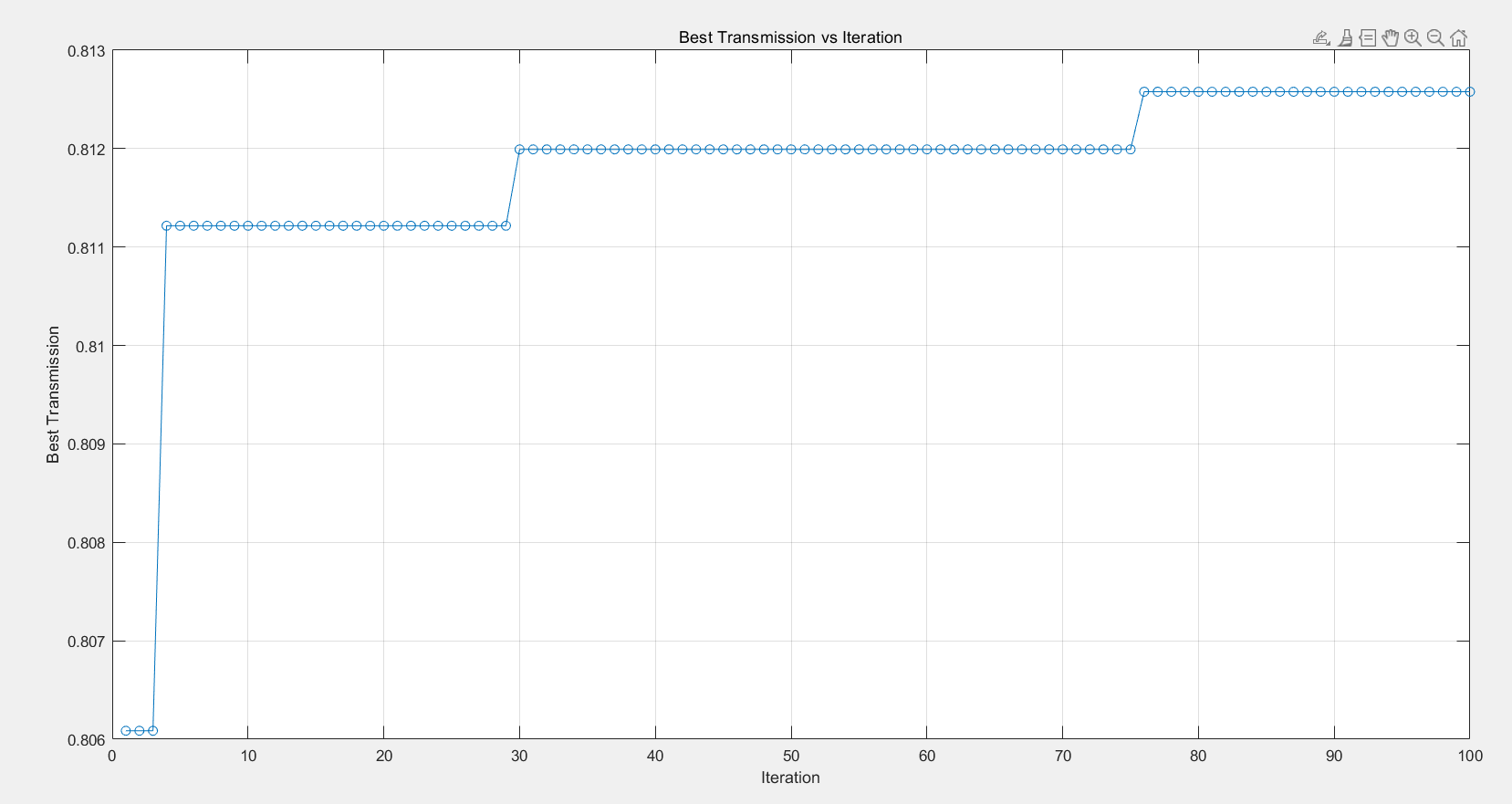
Figure 2. Best Transmission vs Iteration (Photo credit: Original).

This graph shows the optimal transmission rate found by the ant colony algorithm during 100 iterations as a function of the number of iterations. As the number of iterations increases, the optimal transmission rate gradually increases and stabilizes after approximately 60 iterations, indicating that the algorithm is gradually optimizing the thickness configuration of the glass to maximize the amount of solar energy transmitted into the room. Jump points in the graph indicate that the algorithm found a significantly better thickness combination at a particular iteration [10].

These thickness values were obtained after having applied the ACO algorithm for 100 iterations, whereby 50 ants were used in each iteration. The goal was to ensure that the total amount of energy passing through the layers of glass over the range of 300-2000 nm was as great as possible. The result shows that the chosen thicknesses ensure moderate configuration that enables maximum permissiveness of the glass to sun light besides preventing destructive interference and reflection within the layers.

The ACO algorithm tested out several thicknesses and it supported the chosen thicknesses which correspond to higher transmittance value. The trend toward these specific thicknesses suggest that the algorithm found the optimal solution because it was able to travel through this abstract search space by some search strategy while at the same time fixating on the known good thicknesses.

The present application reveals strengths of the ACO algorithm in solving optimization problems where the solution space is huge, and the objective function is non-linear. The thicknesses thus determined guarantee that a maximum of solar energy can be absorbed, especially desirable for increasing internal heat in the cold northern winter.

Additional evaluation and interpretation of the results would comprise of evaluating the efficacy of these optimal thicknesses under different environmental conditions or with other optimisation methods. This would provide a more comprehensive understanding of the efficiency and robustness of the ACO-derived solution in practical applications.

4. Discussion

The values of the identified optimal thickness were L1 = 5.9289 mm, L2 = 7.9309 mm, L3 = 3.8462 mm illustrate the algorithm’s capability of optimizing the combination of reflection, absorption, and inter- ference occurring within the glass layers to allow for optimal energy transmission.

Thus, based on ACO algorithm’s performance of this optimization work, it highlights that it is suitable for multiple mode optimization problems. Thus, the stochastic properties of ACO enable the algorithm to search a wide area of the solution space and avoid early convergence to low-quality solutions, which is a major issue in many optimization methods. Using pheromone-based feedback for the choices, ACO guarantees that the most promising areas of the solution space will be further investigated, thus, making the approach converge toward the best solution.

It is also safe to conclude that the three glass layers are closely balanced when the given results have been attained. The small difference in thicknesses of L1 and L2 combined with a much thinner L3 indicates that the optimum design process will consider factors such as destructive interference to other wavelengths less than 300-nm or greater than 2000-nm and enhancing constructive interference in the target range. This balance is important in establishing that the glass configuration effectively transmits energy in all the possible wave frequencies and not a region thereof.

Additionally, it is illustrated that ACO can be rather useful in engineering design problems and especially in cases where the design domain is huge and it may be incredibly difficult for the standard methods to reach the best solutions. ACO, due to its iterative characteristic and the possibility to integrate a heuristic information about the problem, is a suitable tool for solving complicated problems like the multi-layered materials utilization in optical systems.

Nevertheless, the study has its limitations so take it with a grain of salt. The model assumes constant and uniform illuminance, ignoring the nonuniformity of solar illumination in practice as well as possible imperfections on material properties. Optimized glass layer performance could be degraded by manufacturing tolerances, material imperfections, and environmental variations (e.g., temperature or angle of incidence). In future research, these factors can be embedded in the optimization model to further refine and lead the ACO method toward more dependable outcomes that are closer to reality. Furthermore, although the ACO algorithm was shown to perform well in this study, it is a parameter-specific approach and performing an optimal selection of parameters such as the number of ants, pheromone rate decay, or exploration-exploitation balance can significantly affect results. Sensitivity analysis on these and other parameters would provide further insights into the robustness of this optimization approach, which could, in turn, aid algorithmic development for better performance under fine-tune scenarios. In summary, ACO for glass layer thicknesses show potential to improve building-integrated solar transmission mainly in heating cold climates. The results will help in further research, and can prove helpful for the practical implementations which could be useful to work towards energy-efficient building design or sustainable architectural practices.

5. Conclusion

This study successfully implemented the Ant Colony Optimization (ACO) algorithm to determine the optimal thickness of three glass layers, specifically L1 = 5.9289 mm, L2 = 7.9309 mm, and L3 = 3.8462 mm, to enhance the transmission of solar energy into indoor environments. The findings demonstrate that ACO is an effective tool for solving complex multi-modal optimization problems, particularly in scenarios that involve balancing multiple constraints and parameters, such as minimizing reflection and destructive interference while maximizing constructive interference across a broad wavelength range (300 to 2000 nm). The optimized glass thicknesses resulted in a significant improvement in solar energy transmission, which is critical for enhancing indoor heating during the winter months and thereby increasing energy efficiency in architectural design.

While the study provides a strong foundation for the application of ACO in optimizing multi-layered glass structures, further research is needed to refine the optimization model by considering real-world variables such as material imperfections, environmental variations, and non-uniform solar illumination. Future studies should also explore the integration of ACO with other optimization techniques or machine learning approaches to further enhance the robustness and adaptability of the algorithm. Additionally, conducting sensitivity analyses on ACO parameters, such as the number of ants and pheromone decay rates, could yield deeper insights into the algorithm's performance under various conditions. Expanding this research could contribute significantly to the development of sustainable building technologies and advanced material designs, ultimately improving energy efficiency in modern architecture.