1. Introduction

Automobile adaptive cruise control (ACC), sometimes referred to as active cruise control, is a new system that adds the control function of keeping reasonable distance with the vehicle in front on the basis of the constant speed cruise system. Compared with cruise control, it does not require the driver to frequently cancel and set the cruise control function, so as to avoid distracting the driver during driving. In addition, adaptive cruise can automatically control the engine and brakes properly. In other words, models equipped with fixed-speed cruise can only play a role when there is very little traffic and the road conditions are very good, while the applicable scenarios of adaptive cruise are much wider. Ideally, as long as you get on the high speed, you can directly turn on the adaptive cruise, so that it can control its own deceleration and acceleration, and almost completely free the right foot. ACC further considers safety and comfort, can alleviate driving fatigue, and has a broad space for development.

Fu et al. examined three critical factors—efficiency, accuracy, and passenger comfort—and utilized the DDPG algorithm to address autonomous braking by closely analyzing both lane changes and braking processes [1]. Zhang et al. introduced the use of the Catmull-Rom spline used for modeling lane markings, which offers greater stability and simplicity in construction compared to cubic polynomials, along with enhanced accuracy [2]. Liu et al. developed the AD-GNN framework for predicting adaptive traffic flow using a neural network, which integrates gated time convolutional networks with diffusion convolutional networks to simulate spatial-temporal relationships [3]. Zhang et al. also created an adversarial pedestrian detection model, employing adversarial learning during training, which enhanced detection accuracy by 18.45% and delivered real-time processing at 318 frames per second [4]. Jin et al. applied the 3D-EAFF model, along with trajectory deletion and update strategies, to enhance the tracking accuracy of 3D multi-object tracking (MOT) [5]. Desjardins et al. used function approximation and gradient descent algorithms to refine automatic vehicle control strategies, enhancing the performance of cooperative adaptive cruise control (CACC) [6]. Finally, Chen et al. designed a path planning strategy leveraging deep reinforcement learning to reduce vehicle fuel consumption while meeting task deadlines [7]. This paper focuses on adaptive cruise control, employing the DDPG algorithm from deep learning to implement speed and distance control modes by adjusting for speed and distance errors.

2. Background Knowledge

Deep reinforcement learning (DRL) is an AI method that simulates human decision-making by combining the perceptive abilities of deep learning with the decision-making mechanisms of reinforcement learning. This approach allows control to be exercised directly based on visual inputs. The remarkable achievements of deep reinforcement learning, particularly demonstrated by AlphaGo, have drawn considerable attention from the global research community. Its effectiveness in making decisions under complex conditions highlights its potential. The complexity of vehicle operation, which requires analyzing large volumes of detected data and making real-time decisions, aligns well with the strengths of deep reinforcement learning. Figure 1 illustrates the key components and processes involved in reinforcement learning.

Figure 1. Component composition and process of reinforcement learning.

The agent engages with its environment by taking actions, which in turn cause the environment to change and yield a reward. Through repeated interactions, the agent acquires knowledge through a process of trial and error to develop an optimal strategy. This process, involving trial and error with delayed feedback, is referred to as a Markov decision process. A Markov decision process is characterized by a tuple \( \lt S,A,P,r \gt \) , where \( S \) represents the set of all potential states, \( A \) represents the set of all potential actions, \( P \) represents the probability of state transition (i.e., the likelihood of moving from state \( s \) to state \( {s^{ \prime }} \) after taking action \( a \) ), and \( r(s,a) \) is the reward function, which specifies the reward earned from executing action \( a \) in state \( s \) . During each interaction cycle, the agent traces an interaction trajectory, and the cumulative return at a given state is calculated as follows: \( ({s_{1}},{a_{1}},{r_{1}},{s_{2}},{a_{2}},{r_{2}},⋯,{s_{T-1}},{a_{T-1}},{r_{T-1}},{s_{T}},⋯){s_{t}} \)

\( {R_{t}}=γ{r_{t+1}}+{γ^{2}}{r_{t+2}}+{γ^{3}}{r_{t+3}}+⋯=\sum _{k=0}^{∞}{γ^{k}}{r_{t+k+1}} \) (1)

Where \( γ∈[0,1] \) represents the discount factor, which determines how future rewards are valued relative to immediate ones. A higher value of \( γ \) places more emphasis on long-term rewards, while a lower value focuses more on short-term gains. The main goal of reinforcement learning is to optimize the expected cumulative reward, expressed as:

\( π(a|s)=arg\underset{a}{max}E[R] \) (2)

To determine the optimal strategy, we can introduce the value function and the state-action value function. The value function is defined as:

\( {V_{π}}(s)={E_{π}}[\sum _{k=0}^{∞}{γ^{k}}{r_{t+k+1}}|{s_{t}}=s]={E_{π}}[{r_{t+1}}+γ V({s_{t+1}})|{s_{t}}=s] \) (3)

The state-action value function is defined as:

\( {Q_{π}}(s,a)={E_{π}}[\sum _{k=0}^{∞}{γ^{k}}{r_{t+k+1}}|{s_{t}}=s,{a_{t}}=a] \) (4)

Then the optimal state-behavior function corresponding to the optimal strategy is satisfied:

\( {q^{*}}(s,a)=\underset{π}{max} {q_{π}}(s,a) \) (5)

3. ACC Based on DDPG Algorithm

The Deep Deterministic Policy Gradient (DDPG) algorithm is a deep reinforcement learning method specifically created to address issues in continuous action spaces. It integrates deterministic strategies with the concept of experience replay. DDPG operates on a framework based on the actor-critic model, where the Actor is tasked with learning deterministic policies—outputting specific action values for a given state. Meanwhile, the Critic’s role is to learn the value function and assess the current state. Unlike traditional policy gradient methods, DDPG uses deterministic strategies that output exact action values rather than probabilities, making it more effective in continuous action spaces. Before training begins, the network architecture and parameters for both the Actor and Target-Actor, as well as the Critic and Target-Critic, are identical. During training, the parameters of the Target-Actor and Target-Critic networks are updated according to formula (5):

\( \begin{cases}\begin{matrix}{θ^{Q \prime }}=τ{θ^{Q}}+(1-τ){θ^{Q \prime }} \\ {θ^{π \prime }}=τ{θ^{π}}+(1-τ){θ^{π \prime }} \\ \end{matrix}\end{cases} \) (6)

Where \( {θ^{{Q^{ \prime }}}} \) , \( {θ^{Q}} \) , \( {θ^{π}} \) , \( {θ^{π \prime }} \) represent the parameters for the Target-Critic, Critic, Target-Actor, and Actor networks, respectively. Additionally, \( τ≪1 \) governs the rate of parameter updates. The anticipated gradient of the action-value function aligns with the gradient of the deterministic policy function:

\( {▽_{θ}}J({μ_{θ}})={E_{{μ_{θ}}}}[{▽_{θ}}{μ_{θ}}(s){▽_{a}}{Q^{μ}}(s,a){|_{a={μ_{θ}}(s)}}] \) (7)

The spacing strategy employed in this paper utilizes the fixed time interval approach (CTH). In the CTH method, the time gap between vehicles is kept constant, and the distance relative to the vehicle ahead is directly related to its speed. For safety purposes, the strategy includes a minimum safe distance, outlined in the following formula \( {t_{{​_{H}}}} \) :

\( Δ{x_{des}}={t_{h}}{ν_{H}}+{x_{0}} \) (8)

In this formula, \( Δ{x_{des}} \) represents the desired relative distance between the vehicles, \( {t_{h}} \) is the time gap, \( {ν_{H}} \) is the speed of the leading vehicle, and \( {x_{0}} \) is the minimum safe distance to follow. The MATLAB/Simulink simulation flowchart for the algorithm utilized in this study is displayed in Figure 2.

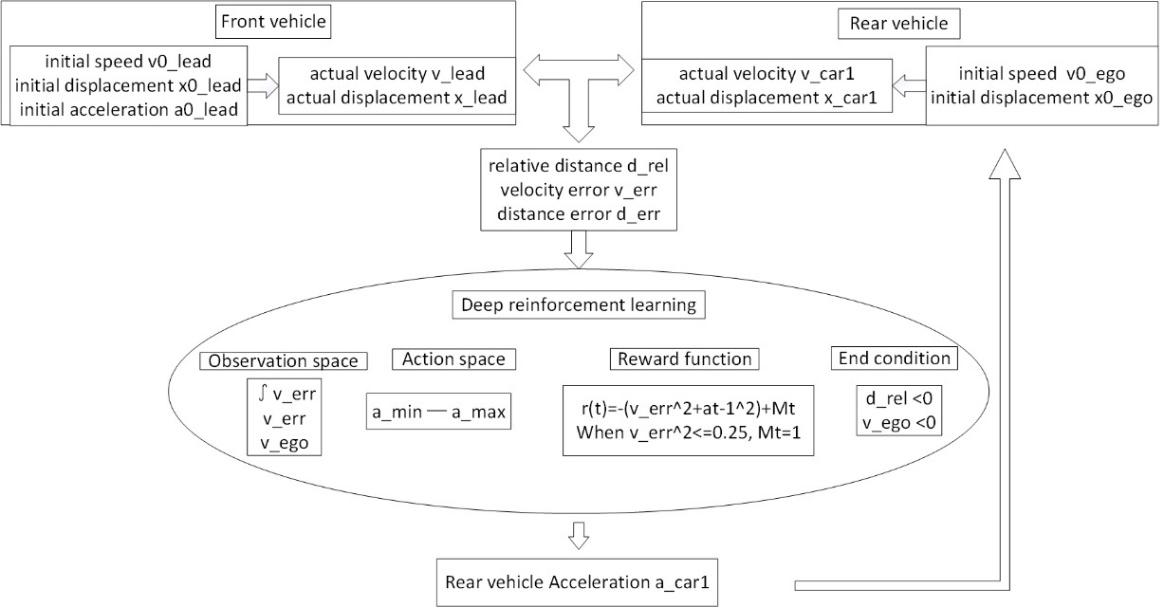
Figure 2. MATLAB/Simulink simulation flow chart.

4. Experimental Results

The hardware setup for the algorithm in this study includes an AMD R7 5800H processor with Radeon Graphics, 16GB of DDR4 3200MHz RAM (8GB × 2), an M.2 2280 512GB SSD, and an NVIDIA GEFORCE RTX 3050 GPU. The software environment is Windows 10 Home (Chinese 64-bit) running Matlab R2022a with Simulink. Figure 3 displays the safety distance and relative distance curves, while Figure 4 illustrates the displacement curve.

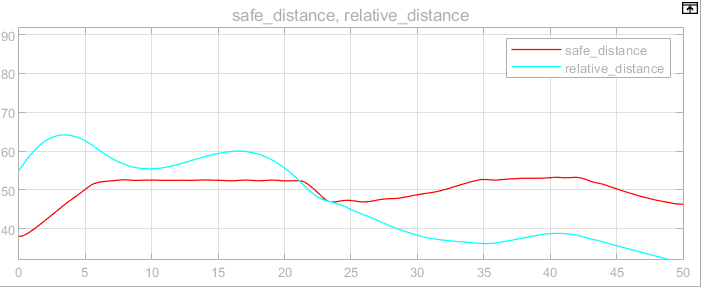
Figure 3. Safety distance and relative distance curve.

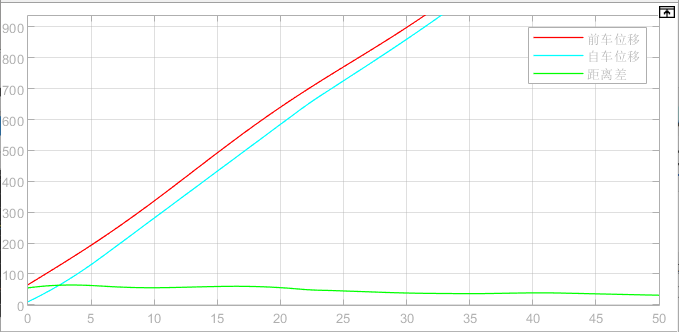
Figure 4. Displacement curve.

As shown in the figure, the relative distance between the two vehicles exceeds the safe distance during the first 23 seconds. After 23 seconds, the relative distance falls below the safe distance, but the gap between the two vehicles stabilizes. Figure 5 presents the acceleration curve of the leading vehicle.

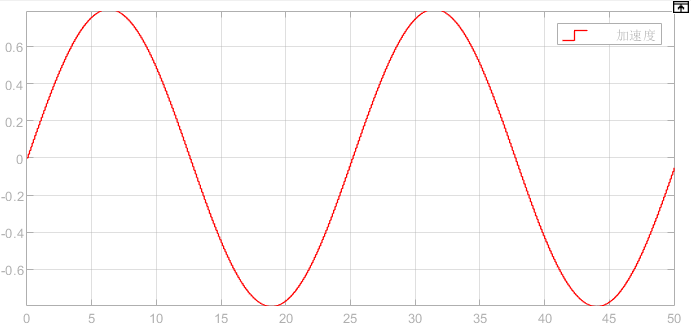
Figure 5. Acceleration curve of the front vehicle.

In this study, the initial acceleration of the leading vehicle is defined as 0.8sin (0.25ωt). The speed curve is depicted in Figure 6.

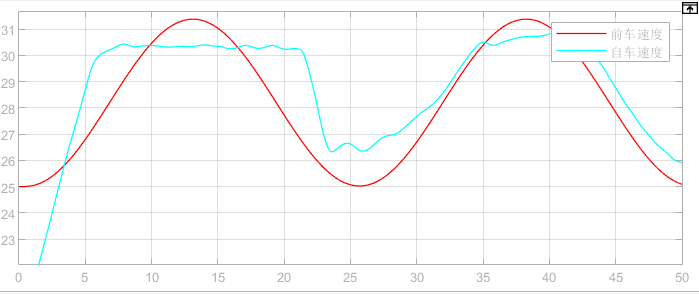
Figure 6. Speed curve.

The figure shows that before 23 seconds, the relative distance surpasses the safe threshold, and the system operates in speed control mode, maintaining the vehicle speed at around 30 m/s. After 23 seconds, when the relative distance drops beneath the safety threshold, the system switches to distance control mode, with v_ref=min {v_lead, v_set}. The acceleration curve for this vehicle is presented in Figure 7.

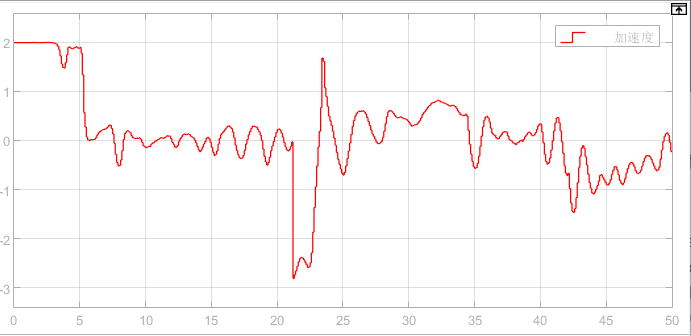
Figure 7. Acceleration curve of the vehicle.

The acceleration curve of the leading vehicle indicates that the acceleration varies over time during both the speed control and spacing control modes. Figure 8 illustrates the reward value curve, which shows rapid convergence. This demonstrates the effectiveness of using reinforcement learning to implement adaptive cruise control (ACC) efficiently.

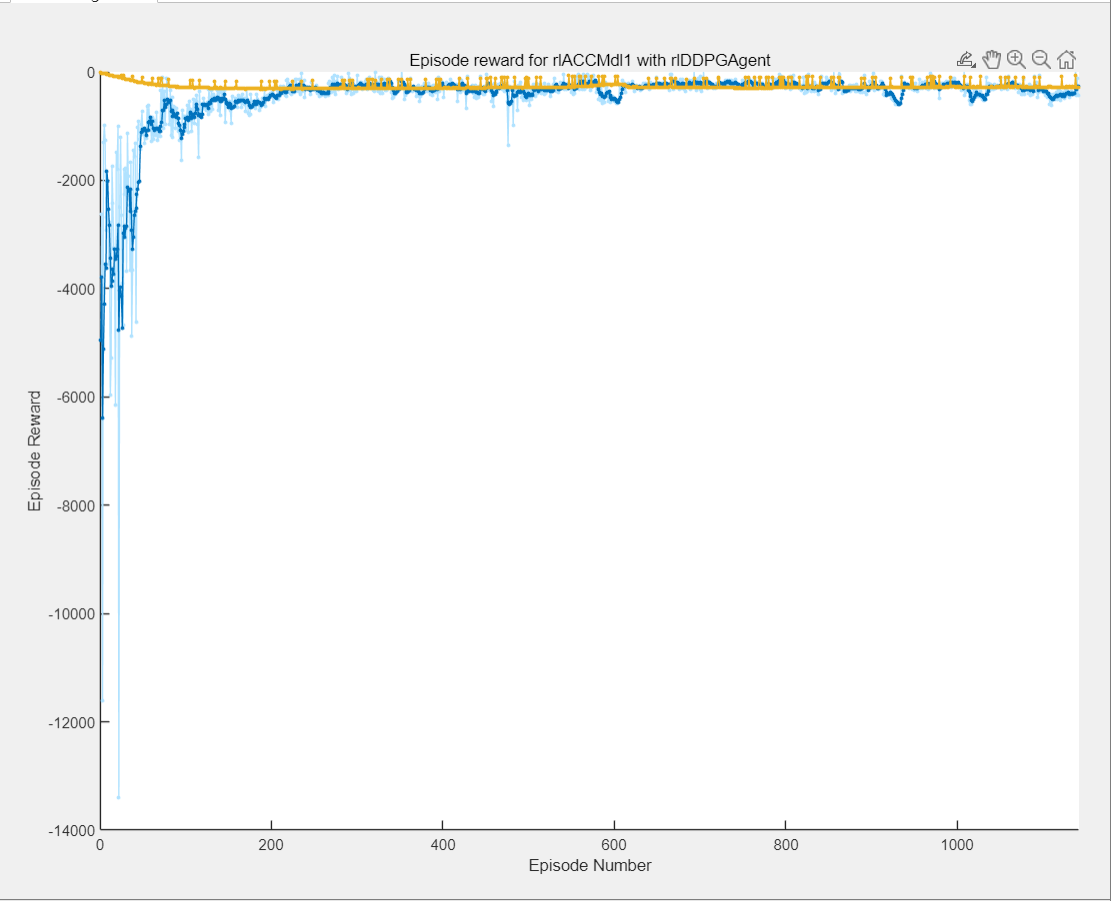
Figure 8. Reward value curve.

5. Conclusions

This paper focuses on adaptive cruise control (ACC) and implements it using the DDPG (Deep Deterministic Policy Gradient) algorithm within deep learning. By incorporating functions for speed error and distance error, two control modes—speed control and distance control—are established along with a reward value function. The algorithm is tested and validated through simulations in MATLAB/Simulink. The experimental results confirm that the DDPG algorithm successfully handles both control modes using deep reinforcement learning. While this study considers a scenario involving two vehicles, real-world traffic conditions often involve three or more vehicles. Future research will aim to enhance model performance by extending the approach to multi-vehicle scenarios using deep reinforcement learning.