1. Introduction

The realm of digital communication and information security has perpetually evolved to counteract the ever-increasing threats of data breaches and unauthorized access. Among the myriad of cryptographic techniques employed to safeguard data, public key cryptography stands out, with the RSA (Rivest-Shamir-Adleman) algorithm, introduced in 1977, being one of its most enduring pillars [1]. This algorithm has not only anchored the confidentiality of digital communications but has also facilitated the expansion of secure operations across various technological spheres, reflecting a growing dependency on robust cryptographic mechanisms.

In the current landscape, the RSA algorithm's applications have transcended simple data encryption to become integral components in securing complex systems, including microcontrollers and digital image transmissions [2]. These areas are particularly sensitive to security breaches due to the ubiquity of digital images and the increasing incorporation of microcontrollers in everyday devices. As technology continues to advance, the need for enhanced cryptographic methods that can operate efficiently within these frameworks grows, driving research into not only the application but also the optimization of existing cryptographic practices.

This paper focuses on exploring the RSA algorithm's application in two primary areas: image encryption and microcontroller security. It delves into the practical implementation of RSA in securing image data through chaotic encryption techniques and in safeguarding communications within microcontroller environments using Arduino platforms [3]. Through experimental setups and security analyses, this study evaluates the effectiveness of RSA in these domains and discusses its potential limitations and future directions. The research aims to contribute to the ongoing discourse on cryptographic security, emphasizing RSA's adaptability and resilience in facing modern digital challenges.

2. Overview of RSA principles

2.1. Basic concepts of the RSA algorithm

RSA algorithm is an asymmetric encryption algorithm proposed by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977 [3]. Asymmetric encryption employs a pair of keys: a public key and a private key. The public key is utilized for encrypting data, whereas the private key serves to decrypt data. RSA stands as one of the earliest widely adopted public key encryption algorithms.

2.2. Workflow of the RSA algorithm

2.2.1. Select two large prime numbers: randomly select two large prime numbers, P and Q. The method for determining whether a number is prime involves trial division, the simplest approach. If there exists a positive integer a and another number b, where b is less than or equal to the square root of a, and a is divisible by b, then a is not prime [4]. Conversely, if no such b exists, a is prime. When using Python to determine if a positive integer a is prime, it is unnecessary to iterate through all numbers less than a. Instead, it suffices to iterate through all positive integers from 2 to the square root of a to check for divisibility [5].

The Python implementation code is as follows:

import math

def is_ prime(a):

if a <= 1:

return f"{a} is not a prime number."

sqrt_ a = int (math. sqrt (a))

for i in range (2, sqrt_ a + 1):

if a % i == 0:

return f"{a} is not a prime number."

return f"{a} is a prime number."

n = int (input ("Please enter a positive integer: "))

result = is_ prime(n)

print(result)

2.2.2. Calculate the modulus n: compute n = p × q. The modulus n is used to generate public and private keys, and it also serves as the modulus in the encryption and decryption processes [6].

The calculation and utilization of the modulus n constitute a pivotal aspect of the RSA algorithm, where the factors p and q of n must be kept confidential. If they are compromised, the RSA algorithm system will be compromised.

2.2.3. To calculate the Euler's totient function φ(n), the formula is φ(n) = (p - 1) × (q - 1). The Euler's totient function is defined as the number of positive integers less than n that are coprime to n [7].

Mathematically, it is expressed as φ(n) = | {k | 1 ≤ k ≤ n, gcd (k, n) = 1} |.

In the context of the RSA algorithm, the modulus n is given as the product of two prime numbers and q.

Therefore, for the Euler's totient function φ(n) in RSA, it holds that φ(n) = (p - 1) × (q - 1).

2.2.4. Select the public key exponent e: Choose an integer e that satisfies 1 < e < φ(n) and gcd (e, φ(n)) = 1. Typically, e = 65537 is preferred due to its excellent balance between security and efficiency. Here, it is crucial to verify that the greatest common divisor (GCD) of e and φ(n) is 1, often achieved using the Euclidean algorithm or the repeated division method. For any two integers a and b (assuming a > b), their GCD is equivalent to the GCD of b and the remainder of a divided by b [8]. Mathematically expressed, GCD (a, b) = GCD (b, a mod b). If b equals 0, then GCD (a, b) is simply a.

Otherwise, update a to be b and b to be the remainder of a divided by b, and repeat the process. This algorithm gradually reduces the larger number until the remainder becomes zero, at which point the divisor represents the greatest common divisor.

In Python, this can be implemented as follows:

def gcd (a, b):

while b! = 0:

a, b = b, a % b

return a

2.3. Security analysis of the RSA algorithm

2.3.1. The challenge of large integer factorization Large integer factorization exhibits immense computational complexity, serving as the cornerstone of RSA algorithm's security. Specifically, the RSA algorithm's public key comprises a large integer n, which is the product of two large prime numbers, p and q. Cracking the RSA key involves extracting these two prime numbers, p and q, from n, posing the notorious large integer factorization problem [9]. Currently, methods for decomposing large integers, such as the General Number Field Sieve (GNFS), encounter significant computational challenges when dealing with numbers exceeding 2048 bits, rendering practical implementation infeasible. Consequently, the security of RSA heavily relies on selecting a sufficiently large key length to enhance the difficulty of factorization.

2.3.2. The irreversibility of modular exponentiation. RSA encryption relies on modular exponentiation, where for a given message m, the encryption process yields c = m^ e mod n. Deriving the plaintext m from the ciphertext c requires the inverse computation of m = c^ d mod n, with d representing the private key exponent [10]. The inherent irreversibility of this modular exponentiation renders it highly challenging to directly extract the plaintext from the ciphertext. Without knowledge of the private key exponent d, this process poses a significant computational hurdle.

3. Application of RSA in Image Encryption

3.1. Chaos-based image encryption scheme

The client generates an RSA key pair: The client utilizes the RSA algorithm to generate a pair of keys, comprising a public key and a private key.

The client transmits the public key to the server: The client forwards the generated public key to the server.

The server encrypts the Logistic Map parameters using the public key: Upon receiving the public key from the client, the server employs the public key to encrypt the parameters of the Logistic Map.

The server relays the encrypted parameters back to the client: The server returns the encrypted Logistic Map parameters to the client.

The client utilizes the private key to decrypt the parameters: Using its own generated private key, the client decrypts the encrypted parameters, revealing the original Logistic Map parameters.

In this process, the RSA algorithm primarily serves to safeguard the security of the Logistic Map parameters during transmission. Since RSA is an asymmetric encryption technique, the public key can be shared openly, whereas the private key remains solely in the possession of the client. Consequently, only the client armed with the private key can decrypt the encrypted parameters received from the server, thereby ensuring the security and confidentiality of the parameters. This encryption approach addresses the challenges associated with key management in symmetric encryption systems based on chaos, thereby enhancing the security of image encryption and transmission. As show in the figure 1.

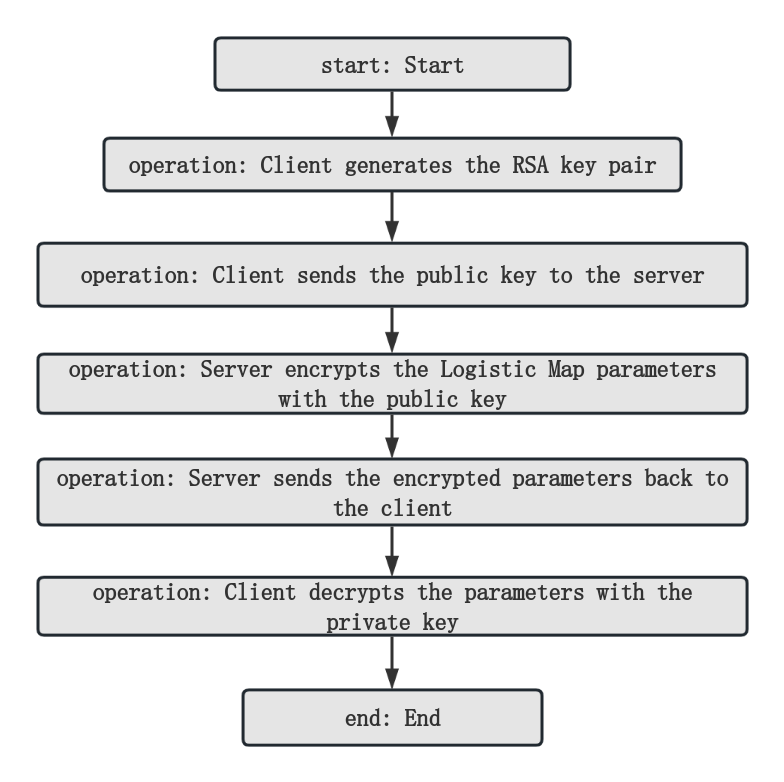
Figure 1. RSA Encryption Process Flowchart for Secure Parameter Transmission (Photo credit: Original).

3.2. Experimental results and analysis

The application of RSA algorithm in this paper primarily aims to safeguard the secure transmission of logistic map parameters during image encryption, thereby addressing the challenges of key management in chaotic-based symmetric encryption systems.

In essence, the process involves the client generating an RSA key pair and transmitting the public key to the server. Subsequently, the server encrypts the logistic map parameters using the public key and relays them back to the client, who then decrypts them with the private key.

Analyzing the merits of this application: Enhanced Security: Through asymmetric encryption, it ensures exclusive decryption access to clients possessing the private key, significantly bolstering the security of parameter transmission.

Addressing Key Management Issues: It effectively resolves the intricacies of key management in chaotic symmetric encryption systems, enhancing the overall security of the image encryption framework.

However, this application is not without potential drawbacks: Computational Complexity: The encryption and decryption processes inherent in RSA algorithm can be computationally intensive, potentially introducing overhead, especially when dealing with vast amounts of data.

Key Length and Performance: The performance of key pair generation, encryption, and decryption can be influenced by the key length, with longer keys potentially leading to slower processing speeds.

Overall, while the application of RSA algorithm offers notable advantages in bolstering the security of image encryption systems, a careful balance must be struck between its security benefits and potential performance implications in practical deployments.

4. Application of RSA in microcontrollers

4.1. Combination of RSA algorithm and arduino

The RSA encryption algorithm, widely employed in public key infrastructure, plays a pivotal role in this research.

Key Generation: The fundamental step in RSA encryption is key generation. In this study, a specialized program is utilized to produce both public and private keys. This process relies on the computational difficulty of factoring large integers. It involves selecting two large prime numbers, calculating their product, and determining related exponents to generate the required keys.

The generated public key serves the purpose of encrypting data, while the private key facilitates the decryption of data encrypted with the public key.

Encryption Process: During the encryption process, the plaintext information entered by the user is captured through the interface between Arduino and the keyboard.

Subsequently, the pre-generated public key is employed to encrypt the plaintext. This encryption step is seamlessly integrated into the Arduino programming, ensuring a smooth hardware implementation.

The encrypted ciphertext can then be displayed on an LCD connected to the Arduino or processed further through a connection with mobile devices.

Decryption Process: Decryption is the inverse of the encryption process. When decrypting ciphertext, the relevant information is retrieved through the connection between Arduino and the associated devices.

Utilizing the private key generated earlier, the ciphertext is decrypted, reverting it back to its original plaintext form.

Similar to encryption, the decrypted plaintext can be displayed on an LCD or processed on other devices as needed.

Hardware Connection and Implementation: Connection between Arduino and Keyboard: The keyboard utilized in this study, a 4x4 matrix, features eight output lines that are connected to pins 2 through 9 of the Arduino (mega 2560) board. The keyboard's functionality is integrated into the Arduino programming, enabling it to capture user inputs such as plaintext, keys, and other relevant data.

LCD Connection: The LCD is seamlessly integrated with the Arduino through a keypad and a breadboard. The specific connections include the LCD's RS pin linked to the Arduino's digital pin 12, the Enable pin connected to digital pin 11, and the D4 to D7 pins wired to digital pins 5 to 2. The R/W pin is grounded, while a 10K resistor is connected between +5V and ground, with its wiper attached to the LCD's VO pin (pin 3). This configuration allows the Arduino to control the LCD, displaying messages like "Hello World!", "Encryption," and "Decryption."

Integrated Keyboard and LCD: By connecting the Arduino, keyboard, and LCD together, a comprehensive encryption setup is established. The user can select either "Encryption" or "Decryption" through the keyboard interface and enter the necessary information, including public/private keys, the value of N, and the text to be encrypted or decrypted. The Arduino processes this information accordingly, encrypting or decrypting the data and displaying the results on the LCD.

Connecting LCD, Keyboard, and Mobile Devices: This setup further extends the encryption capabilities by integrating mobile devices. Once the necessary code is uploaded to the Arduino, the mobile device presents two options: "Encryption" and "Decryption." In the encryption mode, the user is prompted to enter the public key, the value of N, and the text to be encrypted. Similarly, in the decryption mode, the user provides the private key, N, and the ciphertext to be decrypted. This allows users to leverage the RSA encryption program running on a computer to perform encryption and decryption operations remotely through the mobile device.

In conclusion, RSA encryption, through its key generation, encryption and decryption processes, and seamless integration with hardware devices, effectively secures text information. This encryption methodology holds significant value in safeguarding information security.

4.2. Specific steps of software and hardware implementation

Software implementation steps: Utilizing Visual Basic 6, a graphical user interface (GUI) application is crafted, encompassing three pivotal stages: key generation, encryption, and decryption.

During the key generation phase, the program's objective is to generate the necessary public and private keys for the RSA algorithm, leveraging specific algorithms and logic. This intricate process involves complex mathematical computations, such as selecting large prime numbers, calculating the modulus, and determining the Euler function, to ensure the generated keys possess adequate security and reliability.

In the encryption phase, the application presents two distinct fields - one for entering plaintext and another for displaying the resulting ciphertext. Once the user inputs the plaintext into the designated field, the program employs the public key to encrypt the plaintext, thereby generating the corresponding ciphertext.

Conversely, in the decryption phase, the program reverses the encryption process. Upon the user entering the ciphertext, the program utilizes the private key to decrypt the ciphertext, effectively reverting it back to its original plaintext form.

Hardware Implementation Steps. Connecting Arduino to the Keyboard: A 4x4 keyboard, equipped with 8 output lines for transmitting keystroke information, is chosen.

The eight output lines of the keyboard are sequentially connected to pins 2 through 9 of the Arduino (mega 2560), ensuring that the Arduino can effectively receive input signals from the keyboard.

Within the Arduino programming, specialized keyboard driver code must be written to interpret signals emanating from the keyboard and translate them into recognizable input data.

Connecting the LCD: Connecting the LCD, keypad, and breadboard necessitates adherence to specific circuit connection protocols. Precisely, the RS pin of the LCD is wired to digital pin 12, the Enable pin is linked to digital pin 11, and the D4 to D7 pins are respectively connected to digital pins 5 to 2. The R/W pin is grounded, while a 10K resistor is positioned with one end connected to +5V and the other to ground, with its wiper terminal connected to the VO pin (pin 3) of the LCD.

Upon completion of the physical connections, corresponding code must be written within the Arduino program for verification purposes, to guarantee that the LCD functions properly and displays the desired information accurately.

Connecting Keyboard and LCD: The Arduino, keyboard, and LCD are seamlessly integrated to create a comprehensive input-output system.

Within the Arduino software, encryption-related code is crafted to empower the LCD to showcase two crucial options: "Encryption" and "Decryption".

Users can navigate through the keyboard to select their desired operational mode and proceed to input pertinent information, including plaintext and keys. Depending on the input, the Arduino performs either encryption or decryption operations, promptly displaying the outcomes on the LCD.

By writing specialized code within the Arduino software, mobile devices are enabled to seamlessly interact with hardware systems. Upon connecting the mobile device to the system, two options are presented: "Encryption" and "Decryption".

In the "Encryption" mode, the mobile device prompts the user to input a series of information, comprising: a) public key, b) N, and c) a combination of text 1 and text 2. Once the user provides these details as per the prompts, the Arduino utilizes the public key to encrypt the text.

Switching to the "Decrypt N, and c) a concatenation of ciphertext 1 and ciphertext. Upon receiving these inputs, the Arduino employs the private key to decrypt the ciphertext, revealing the original plaintext.

Throughout this process, the user leverages the public key, private key, and N generated by an RSA encryption program on a computer, ensuring the precision and security of both encryption and decryption operations.

In conclusion, this research has capitalized on the strengths of the RSA algorithm, realizing the functionalities of information encryption and decryption through meticulously designed software and hardware implementation steps. Furthermore, by facilitating the connection and interaction of diverse hardware devices, it enhances the system's flexibility and usability, offering a viable solution for the realm of information security.

5. Conclusion

This study extensively explores the application of the RSA algorithm in image encryption and microcontroller security, demonstrating its vital role in enhancing data protection in these domains. The research underscores RSA's capability to effectively secure image data and microcontroller communications, leveraging its robust encryption mechanisms. By integrating RSA with chaotic encryption techniques, the security of image data transmission is significantly enhanced, proving superior to traditional encryption methods. Additionally, the successful implementation of RSA in Arduino-based microcontrollers showcases its adaptability in securing embedded systems, crucial for the Internet of Things (IoT) applications.

Future research will focus on addressing the inherent challenges and extending the capabilities of the RSA algorithm. As computational demands and quantum computing pose potential risks to RSA's effectiveness, it is imperative to explore more efficient cryptographic techniques and develop quantum-resistant algorithms. Further refinement of hybrid encryption methods will also be critical to optimizing data security across various platforms. By advancing these areas, the RSA algorithm can continue to provide robust security solutions, adapting to the evolving demands of digital security technologies.