1. Introduction

Greenhouses are essential for off-season crop cultivation by providing controlled environments optimal for plant growth, including appropriate temperatures, nutrients, and light intensity. Crucial to this control is the management of light transmittance through the greenhouse coverings, which not only influences plant growth but also affects various physiological aspects such as soil microbial activity and chlorophyll content in plants [1-3]. Innovations in greenhouse environmental control have incorporated various intelligent control methods like fuzzy, decoupling, artificial intelligence, and phenotype controls to optimize conditions [4]. Advanced techniques and frameworks continue to evolve, drawing from diverse fields such as immunology for intelligent algorithm design [5] and artificial neural networks for improved prediction of climate parameters [6]. Furthermore, efforts to enhance resource efficiency in arid conditions and improve control accuracy through predictive algorithms and adaptive models are ongoing [7,8].

Despite extensive research on optimizing greenhouse conditions, there is a notable gap in studies focusing on the optimization of greenhouse glass thickness—a common element in greenhouse construction that significantly affects energy capture and efficiency [9]. The thickness of the glass directly impacts the amount of light that can penetrate the greenhouse, affecting the energy available for plant growth [10]. Given the quantum genetic algorithm’s (QGA) capability in handling multi-objective optimization problems and its success in fields like building structure optimization and large-scale network management, it stands out as a promising tool for this application [11,12].

This paper applies the quantum genetic algorithm to optimize the thickness of multi-layer glass in greenhouses to maximize light transmittance and energy utilization. Focusing on three layers of glass, we simulate direct sunlight conditions at noon, modeling the physical process of light penetration before optimizing the glass layers' thickness with QGA. The results not only yield the optimal combination of glass thicknesses for maximum emergent light energy but also demonstrate the superiority of QGA over classical genetic algorithms and random number optimization methods. By enhancing the transmittance of insulating glass, this study contributes significantly to increasing the total energy available to plants within the greenhouse, showcasing the potential of QGA in agricultural applications [13,14]. literature review

2. Literature review

To enhance greenhouse performance, various advanced environmental control methods have been explored. These methods include fuzzy logic, decoupling control, and artificial intelligence (AI) approaches, which collectively aim to achieve optimal greenhouse climate conditions . In particular, AI and machine learning techniques have shown significant promise in predicting climate parameters and controlling greenhouse environments. For instance, neural networks have been used to model greenhouse conditions accurately, allowing for better prediction and control of temperature and humidity . Other approaches, such as adaptive models and predictive algorithms, have been specifically employed to improve resource efficiency and control accuracy in greenhouse settings, demonstrating the broad applicability of intelligent control frameworks [3]. Despite the progress in greenhouse control technologies, there is a notable lack of focus on optimizing the thickness of greenhouse glass, which is crucial for maximizing light transmittance and energy efficiency. Previous studies on glass optimization in greenhouse design have primarily concentrated on energy-saving strategies . However, the thickness of the glass, which directly affects the amount of light penetration, remains an underexplored aspect. Given that light availability is one of the fundamental drivers of plant growth, optimizing glass thickness offers a potentially significant avenue for enhancing greenhouse productivity [6]. Quantum genetic algorithms (QGAs) have emerged as a promising tool for addressing multi-objective optimization challenges, including those related to energy efficiency and structural design . QGAs combine the principles of quantum computing with classical genetic algorithms, thereby enhancing the search space and improving the convergence rate. This makes QGAs particularly suitable for complex optimization problems, where they can outperform classical algorithms in terms of both speed and solution quality. Recent applications of QGAs in building structure optimization and large-scale network management demonstrate their potential for tackling energy-related optimization issues. Studies comparing QGAs with classical genetic algorithms reveal that QGAs often yield faster convergence and more optimal solutions, especially in cases where multiple variables and constraints are involved. The application of QGAs to optimize greenhouse glass thickness represents a novel approach that aligns with the recent trend towards integrating quantum computing techniques into agricultural applications. Classical genetic algorithms have been widely applied in greenhouse optimization, focusing on parameters such as temperature and humidity control to enhance crop yield [5]. However, these algorithms typically lack the computational efficiency needed to handle the complex interdependencies involved in optimizing multi-layer glass thickness for light transmittance [6]. By contrast, QGAs offer a more robust solution due to their ability to operate in a superposition state, which allows them to evaluate multiple solutions simultaneously and explore a larger solution space. This characteristic makes QGAs particularly effective for optimizing the transmittance properties of multi-layer glass, ensuring that maximum solar energy is harnessed within the greenhouse. In comparison to random optimization methods, QGAs provide a more structured approach to finding optimal solutions. Random number-based techniques can offer a baseline for performance; however, they lack the precision and adaptability required to identify the best configurations for greenhouse glass thickness [6]. Furthermore, studies have shown that QGAs consistently outperform classical genetic algorithms and random optimization methods in terms of stability and robustness, particularly in scenarios requiring the fine-tuning of multiple parameters [4]. The unique capabilities of QGAs in managing multi-layer configurations and their superior optimization performance underscore their potential as a powerful tool in greenhouse design and beyond. By leveraging QGAs to optimize glass thickness in greenhouses, this study contributes to the broader field of agricultural innovation and material science. The findings demonstrate that QGAs not only enhance light transmittance but also improve the overall energy efficiency of greenhouses, which is essential for sustainable agricultural practices. The study also highlights the versatility of QGAs in various agricultural applications, suggesting future possibilities for integrating quantum computing into smart agriculture and environmental management. In summary, this literature review illustrates the importance of optimizing greenhouse glass thickness for energy efficiency and highlights the significant advantages of QGAs over classical methods. The research underscores the potential of QGAs to revolutionize greenhouse design by offering a reliable, fast, and accurate means of optimizing multi-layer structures, paving the way for more energy-efficient and productive agricultural systems.

3. Algorithm design

3.1. Calculation of emergent light intensity under single-layer glass

As shown in Figure 1, Sunlight vertically enters glass from air. \( {n_{0}} \) is the refractive index of air at 1.0, \( n \) is the refractive index of glass at 1.5, \( {I_{i}} \) is the intensity of the incident sunlight, \( {I_{t}} \) is the intensity of the light transmitting through the glass, \( {I_{r}} \) is the intensity of the light reflected by the glass, and \( L \) is the thickness of the glass. The formula for calculating transmittance can be obtained as follows:

\( T=\frac{{I_{t}}}{{I_{i}}}=\frac{{(1-R)^{2}}}{{(1-R)^{2}}+4R{sin^{2}}⁡(kL)} \) (1)

\( R={(\frac{n-{n_{0}}}{n+{n_{0}}})^{2}} \) (2)

\( k=\frac{2πn}{λ} \) (3)

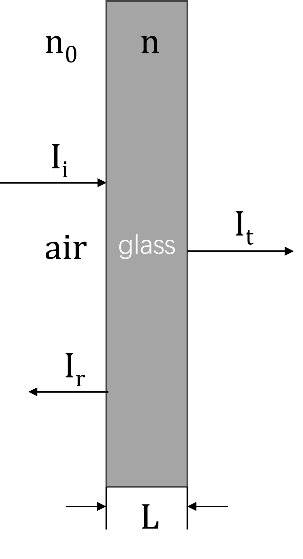
Figure 1. Sunlight injects into a single-layer glass (Photo credit: Original).

The intensity of the incident light is defined as Gaussian distribution in equation (4).

\( {I_{i}}=1000exp⁡(-\frac{(λ-{λ_{0}}{)^{2}}}{2{σ^{2}}}) \) (4)

λ is the wavelength of sunlight, ranging from 300nm to 2000nm, and the center wavelength \( {λ_{0}} \) is selected as 580nm. \( σ \) can be derived from equation (5), with a FWHM of 500.

\( FWHM=2\sqrt[]{2ln2}\cdot σ \) (5)

By plotting \( {I_{i}} \) , we can obtain the Simulated spectrum of incident sunlight as shown in Figure 2.

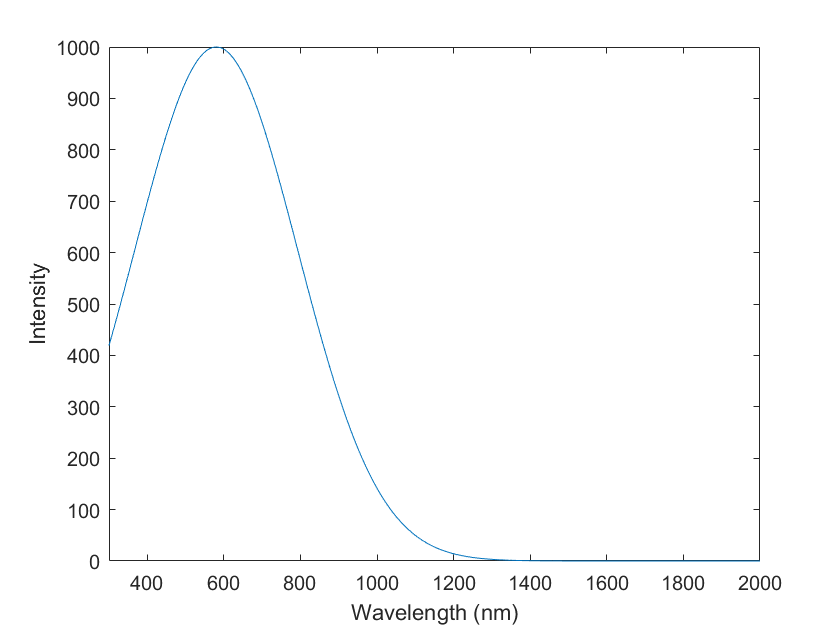
Figure 2. Simulated spectrum of sunlight (Photo credit: Original).

If we can obtain the thickness \( L \) of the glass and substitute it into equation (1) to obtain the transmittance, then the intensity of the emergent light is.

\( {I_{t}}={I_{i}}*T \) (6)

3.2. Calculation of emergent light intensity under multi-layer glass

The situation of single-layer glass mentioned above can be extended to three-layer glass. The thickness of each layer of glass is \( {L_{1}} \) , \( {L_{2}} \) , \( {L_{3}} \) , The emergent light intensity after passing through each layer of glass is \( {I_{t1}} \) , \( {I_{t2}} \) , \( {I_{t3}} \) ,The reflected light intensity is \( {I_{r1}} \) , \( {I_{r2}} \) , \( {I_{r3}} \) , The transmittance of every three-layer glass is \( {T_{1}} \) , \( {T_{2}} \) , \( {T_{3}} \) ｡The final emergent light intensity can be obtained.

\( {I_{t3}}={T_{1}}*{T_{2}}*{T_{3}}*{I_{i}} \) (7)

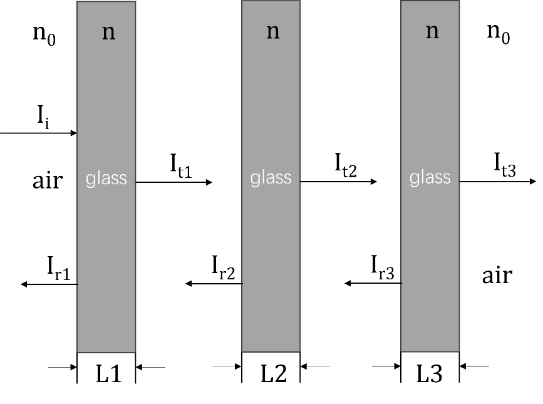
Figure 3. Sunlight injects into a multi-layer glass (Photo credit: Original).

Taking the given thickness of three layers of glass as an example, which are 5mm, 6mm, and 4mm, the transmittance of the glass can be obtained by substituting them into equation (1). Then, by substituting the results into equation (6), the relationship between different wavelengths and the intensity of the emergent light under this glass thickness combination can be obtained as shown in Figure 4.

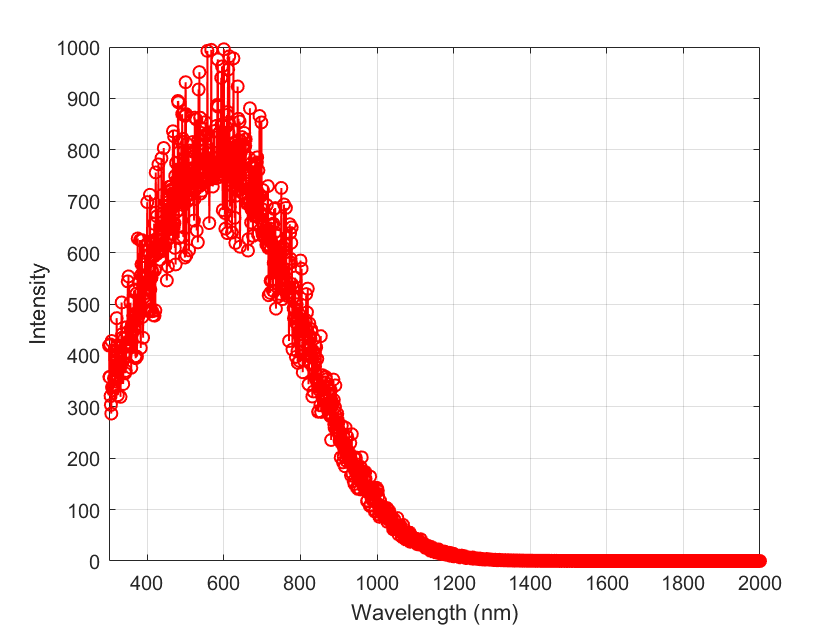
Figure 4. The spectra of sunlight passing through 5mm, 6mm, and 4mm glass (Photo credit: Original).

3.3. Optimization of emergent light intensity using quantum genetic algorithm

Firstly, initialize the population size and individual genes, taking the thickness of three pieces of glass as a variable and using it as a gene. Set a set of glass thickness combinations as one individual, with each individual having three quantum bit. Each quantum bit is in a superposition state which allows quantum bits to have the possibility of both ​|0⟩and |1⟩ simultaneously. Initialize the population using quantum bit encoding, and set the initial state of each quantum bit to a uniform superposition state, and the initial new individual is \( （\frac{1}{\sqrt[]{2}}，\frac{1}{\sqrt[]{2}}，\frac{1}{\sqrt[]{2}}） \) ,which means that the probability of a quantum bit collapsing to ​​|0⟩ and |1⟩ is the same.

Afterwards, the population is measured and the quantum state is converted into binary encoding, and quantum bits collapse from a superposition state to a definite 0 or 1.

The third step is to convert binary encoding into decimal and evaluate the fitness of each individual, Using the thickness of the three-layer glass as the variable, quantum genetic algorithm is used to optimize the final emitted light intensity to maximize it, obtaining the maximum value of the total energy of vertically incident sunlight. The thickness of the glass is limited to 1mm to 1cm. The optimization objective function is

\( I\_total=\int _{300}^{2000}{I_{t3}}dλ \) (8)

By approximating and discretizing the integral, the emergent light intensity at each wavelength can be calculated separately, and the total energy can be obtained by adding them up. If this value is larger, it indicates that the individual is more outstanding.

The fourth step is to update the population using a quantum rotation gate, which can update each individual based on the evaluation results. The more excellent the individual, the smaller the rotation angle of the quantum rotation gate, so the probability of retaining the original gene will increase. On the contrary, if the fitness value is poor, the rotation gate will rotate its quantum bits in the opposite direction, reducing the probability of this state and increasing the probability of it becoming another worthwhile state. The final solution approaches the optimal direction. By iterating through the above steps, the optimal solution can be obtained.

4. Optimization results

4.1. Optimization results of quantum genetic algorithm

Table 1 shows that the algorithm can obtain different combinations of glass thickness, and the final optimized total energy is very similar. Figure 5 shows that the algorithm can converge to the maximum light intensity each time, and the quantum genetic algorithm can obtain results within 300 generations when solving this problem. These indicate that this algorithm is very stable and robust, and can always find the optimal solution, so it can solve the optimization problem of glass thickness in greenhouses.

By substituting the four combinations of glass thickness into the model, the relationship between different wavelengths and light intensity can be obtained as shown in Figure 6.

Table 1. Optimization results of quantum genetic algorithm.

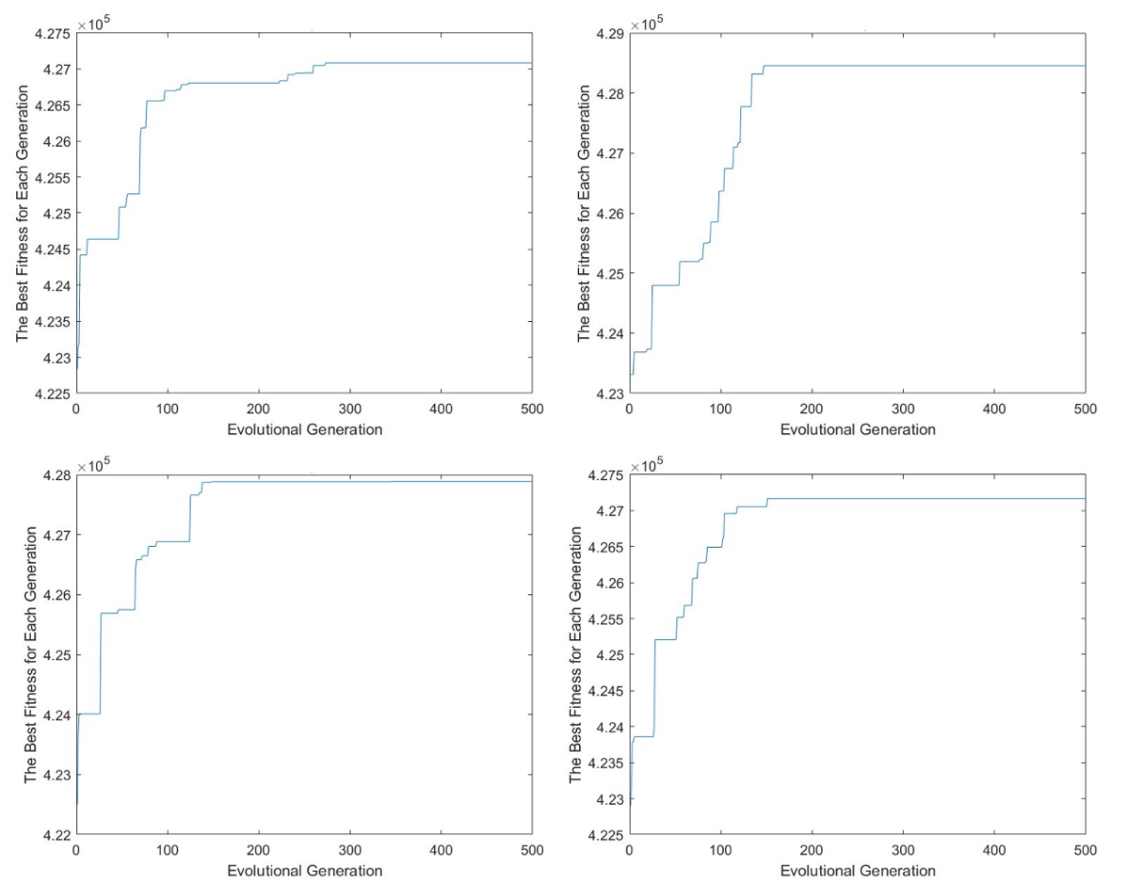
Figure 5. Evolution process diagram corresponding to the four results, with the top left corresponding to the first time, the top right corresponding to the second time, the bottom left corresponding to the third time, and the bottom right corresponding to the fourth time (Photo credit: Original).

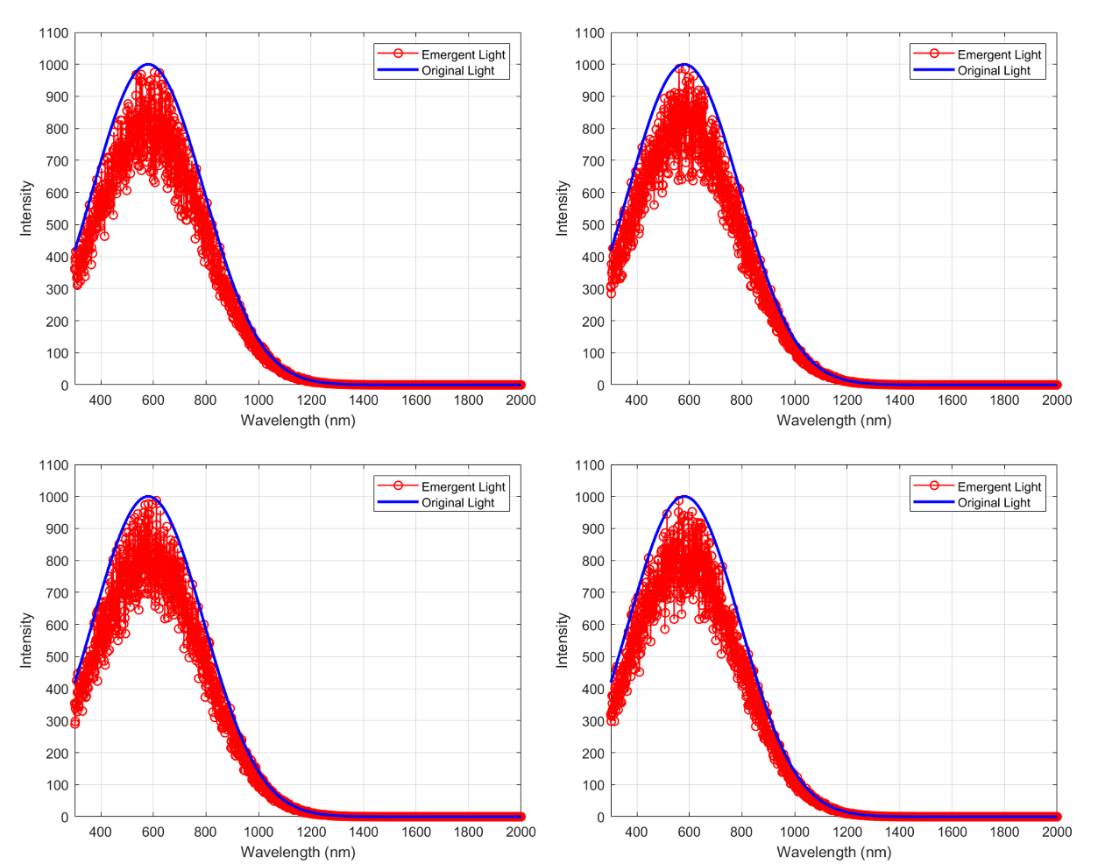
Figure 6. Spectral diagrams corresponding to four glass thickness combinations, with the top left corresponding to the first type, the top right corresponding to the second type, the bottom left corresponding to the third type, and the bottom right corresponding to the fourth type (Photo credit: Original).

From Figure 6, it can be seen that compared to the original light, after passing through three layers of glass, the distribution of the emergent light intensity is still similar to the approximate distribution of the original incident light. However, after passing through three layers of glass, the intensity of some wavelengths of light shifted downwards, and the degree of deviation varied with different combinations of glass thicknesses, resulting in differences in the final intensity of the emitted light. If at each wavelength, the higher the vertical axis, the closer it is to the original light, indicating that the energy loss after passing through the glass is smaller, and the total energy of the light ultimately entering the greenhouse will also be larger.

4.2. Optimization results of classical genetic algorithm and comparison

As shown in Table 2, classical genetic algorithms can also solve this problem. At the same time, random numbers were used to generate the thickness of three layers of glass to simulate the actual situation of selecting glass thickness randomly, and the total energy of the emergent light was obtained as shown in Table 3. By comparing Figure 7, it can be seen that the quantum genetic algorithm obtains the maximum total energy and the best optimization effect, while the classical genetic algorithm also obtains a total energy greater than the randomly generated optimization method. This indicates that in practical situations, selecting glass thickness randomly may lead to energy loss and have a negative effect on crop growth in greenhouses. Overall, quantum genetic algorithm has better advantages in solving this problem.

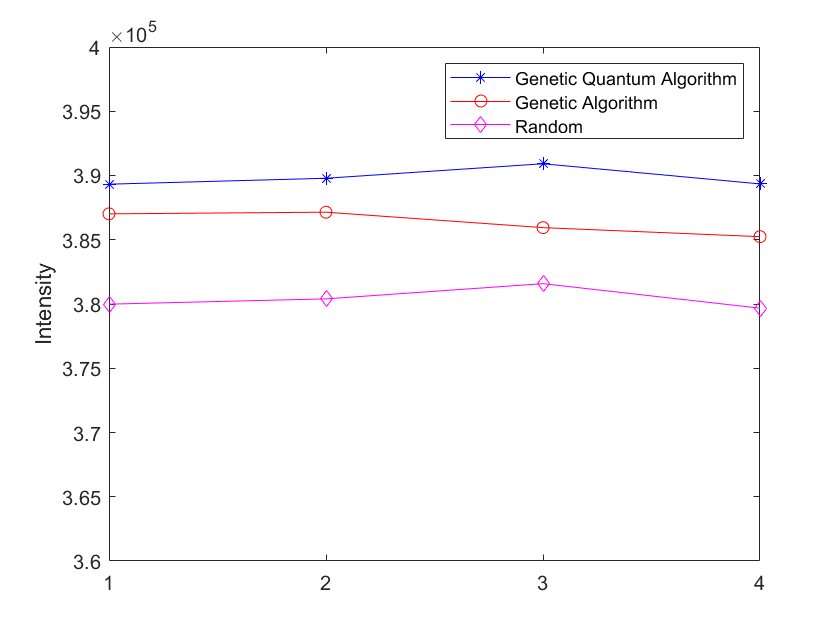
Figure 7. Comparison of quantum genetic algorithm, classical genetic algorithm, and using random numbers (Photo credit: Original).

Table 2. Optimization results of classical genetic algorithm.

Table 3. Optimization results using random numbers.

5. Conclusion

This study effectively demonstrates the application of the quantum genetic algorithm (QGA) in optimizing glass thickness for greenhouse design, providing a robust method to maximize the energy available to crops and enhance yield potential. By tailoring glass thickness, optimal light transmittance and energy utilization are ensured, substantiating the utility of QGA not only in greenhouse applications but also in studying the transmittance properties of multi-layer thin films. The precision of the optimized glass thickness highlights the algorithm’s accuracy and its potential for broader applications in materials science. To address the practical limitations of glass processing, integrating a thin film coating process is suggested to refine the glass further and align it more closely with the optimized parameters. Additionally, exploring the possibility of adjusting the refractory index within the manufacturing process could further enhance the intensity of light transmitted, pushing the boundaries of current greenhouse technology.

Looking ahead, the adaptability of this method could be significantly expanded by considering variable sunlight incidence angles, incorporating the glass angle as a dynamic variable in the greenhouse lighting system. This adaptation would pave the way for a more automated and intelligent lighting regulation within greenhouses, potentially revolutionizing the way light optimization is approached in agricultural settings. Such advancements could lead to more energy-efficient greenhouses that are capable of adjusting in real-time to changing environmental conditions, thus maximizing both energy usage and crop yields in an increasingly sustainable manner.