1. Introduction

The secure transmission and storage of data are paramount in today’s digital age, as society becomes increasingly reliant on information technology. Cryptography serves as the backbone of data security, safeguarding sensitive information across numerous applications. A fundamental challenge in cryptography is the factorization of large integers, which underpins the security of widely used encryption systems, such as RSA. Traditional factorization methods, including trial division and elliptic curve algorithms, have proven inefficient for extremely large numbers. However, with the continuous improvement of computational power and algorithmic sophistication, the demand for more effective factorization techniques has grown significantly [1, 2].

Among various algorithms, the Number Field Sieve (NFS) stands out as one of the most advanced and efficient methods for factorizing large integers, especially those exceeding 110 digits. Its sub-exponential computational complexity makes NFS particularly powerful in cryptographic contexts, such as breaking RSA encryption. The NFS method has been successfully employed in notable achievements, including the factorization of RSA-768, which required approximately 2000 core-years of computational effort, highlighting its capability in tackling large-scale factorization problems [3]. The key processes within NFS—polynomial selection, sieving, matrix solving, and square root extraction—each contribute significantly to its overall efficiency. Recent advancements have focused on enhancing these processes, particularly through parallel computing techniques that reduce computational time and resource demands.

This paper provides a comprehensive review of the NFS algorithm, detailing its foundational principles, key components, and recent research developments. The study systematically examines the four main stages of NFS, highlighting both technical challenges and solutions that have emerged in recent years. By exploring advancements in polynomial selection, lattice sieving techniques, and matrix-solving optimizations, the paper aims to shed light on how NFS has evolved and continues to set new benchmarks in integer factorization. Additionally, the paper discusses future directions for improving the algorithm, focusing on reducing computational complexity and enhancing its practicality for cryptographic applications. This analysis not only underscores the ongoing relevance of NFS but also identifies critical areas for further research in large integer factorization [4-7].

2. Relevant techniques

2.1. RSA

Encryption: Given the public key (e, N) and plaintext M, ciphertext C is calculated by the following formula:

C=E (M) =Me mod N (1)

M=D (C)=Cd mod N (2)

2.2. Advantages of the number field sieve

Large integer factorization is the process of factorizing a large integer into its prime factors. This has important applications in cryptography, especially in some encryption algorithms such as RSA. At present, large number decomposition has completely separated from the era of violent trial division, there are several common large number decomposition methods, such as trial division, ρ method, P-1 method, elliptic curve algorithm, random square method, quadratic sieve method and number field sieve method [4]. In addition, there are quantum algorithms that rely on quantum computers, which can greatly improve the efficiency of decomposition, but quantum computers are still under development. Zeng Yonghong, Liu Xinxing et al. and Yang Lili have made a very good review of large integer decomposition, pointing out that for integers greater than 110 bits, number field screening is the fastest algorithm at present, and its time complexity is as follows [5-7]:

0(exp(( \( \frac{64}{9}+0(1)^{1/3}(logN)^{1/3}(\log{logN)^{2/3}))} \) (3)

The NFS is highly parallelizable, meaning that large-scale computations can be distributed across multiple machines. This feature makes it ideal for use in grid computing and cloud computing environments, where many processors can work together to factor very large numbers efficiently. By solving this congruence, we get the nontrivial factors of N, gcd (N, x + y) and gcd(N, x-y) giving the nontrivial factorization of N with a probability of 2/3. This process is particularly complex and requires a series of mathematical concepts and mappings to finally find the combination of x and y square numbers. The detailed process can be seen in references [8, 9]. These complex theories will eventually solidify into programs. From the point of view of computer science, the number field screening method is mainly divided into four parts, which are polynomial selection, number pair screening, matrix solving, and square root finding, as shown in Figure 1.

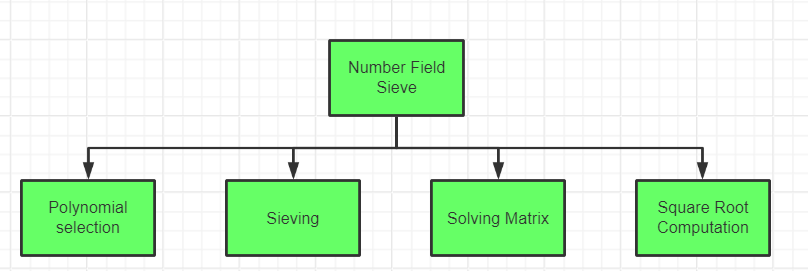
Figure 1. The main process of NFS (Photo credit: Original).

3. Research progress

The special number field sieve method deals specifically with integers that have a particular form or structure. The number field sieve is not an independent algorithm, but a collection of algorithms. The number field sieve method includes the four main calculation processes in the previous chapter, and each process contains one or more dependent algorithms [10].

Polynomial selection. Polynomial selection is the first and key step of the number field screening method, which makes the subsequent number pair screening more efficient. Polynomial selection is mainly the selection of two mutual-prime polynomials f(x), g(x), and the two polynomials have the same root in the module n. An m-based approach is usually used. Namely.

\( \mathbf{n}=\sum_{\mathbf{i}=\mathbf{0}}^{\mathbf{d}}\mathbf{c}_\mathbf{i}\mathbf{m} \) i ,0≤ \( \mathbf{c}_\mathbf{i} \) <m (4)

Get further.

f(x)= \( \sum_{\mathbf{i}=\mathbf{0}}^{\mathbf{d}}\mathbf{c}_{\mathbf{i}\ } \) xi,g(x)=x-m (5)

Finally.

f(m)≡0(mod n), g(m)≡0(mod n) (6)

f(m) and g(m) modules n have the same root m. In 1999, Murthy conducted a systematic study on polynomial selection in his doctoral thesis, and believed that good polynomials could not only generate more number pairs, but also reduce the size of the matrix [11]. Based on the base-M method, the techniques of transformation and rotation are introduced to generate skew and non-skew polynomials. The combination of nonlinear polynomial and non-first linear polynomial is a commonly used technique at present, and nonlinear polynomial is also developing [12, 13]. Prest et al. have extended the nonlinear polynomial method and increased the degree of polynomial generated by the original algorithm, but the practical application is limited at present. Yang et al. analyzed polynomial roots and found that polynomials with more small primes in their tail coefficients could generate more number pairs, and its engineering practicability needs to be further confirmed [14].

It is mainly to decompose the expression of logarithmic pairs (a, b) on the factor basis to find smooth numbers that can be decomposed into the product of small prime numbers. For each a and b, calculate two values [15]:

F(a,b)=bd ∙ f( \( \frac{\mathbf{a}}{\mathbf{b}} \) ),G(a,b)=b ∙ g( \( \frac{\mathbf{a}}{\mathbf{b}} \) ) (7)

F(a,b)= \( \prod_{\mathbf{i}}\mathbf{p}_\mathbf{i}^{\mathbf{e}_\mathbf{i}} \) , G(a,b)= \( \prod_{\mathbf{j}}\mathbf{q}_\mathbf{j}^{\mathbf{f}_\mathbf{j}} \) (8)

Where pi and qj are small prime numbers.

The line sieve is an earlier method proposed within the Number Field Sieve . It works by performing sieving in a fixed linear space to find integers that satisfy specific conditions. While the line sieve is relatively simple, its efficiency is low when dealing with very large integers. The lattice sieve is a more modern method in the NFS, which increases efficiency by performing sieving on a lattice structure. The lattice sieve is more effective in handling large integers and shows significant advantages in practical applications. In 1994, Golliver et al. introduced the operation of trial division to the lattice sieve, further improving its efficiency [16]. In 2005, Franke et al. proposed using continued fractions to enhance the sieving process in the lattice sieve [17]. With the development of computer technology, L.T. Yang et al. and Gad et al. continuously optimized the sieving algorithms in the NFS and significantly accelerated the sieving process by utilizing parallel computing techniques [18-22].

Matrix Solving. Matrix solving refers to the process of constructing linear relations from the smooth numbers obtained during sieving and finding quadratic congruences under modulus N. Initially, Gaussian elimination was used, but the Block Wiedemann algorithm or Block Lanczos algorithm are now predominantly used to solve linear algebra systems over binary fields to obtain several perfect squares, as shown in Figure 2. Yang et al. designed methods to reduce synchronization and communication for parallel Block Lanczos algorithms, obtaining approximately 7 times speedup on 16 cores and 11 times speedup on 30 cores [23-25]. Zhou proposed a custom parallel architecture for the Block Wiedemann algorithm, which can be categorized under Field Programmable Gate Array (FPGA) acceleration [26].

Solving for Square Roots. Solving for square roots refers to the process of obtaining the final factorization result based on the perfect squares obtained from the matrix solving phase. Lenstra et al. introduced the steps for solving square roots in 1993, and several methods have since emerged. Thome reviewed square root-solving methods, which primarily include the direct method, Couveignes’ algorithm, and Montgomery’s algorithm, as shown in Figure 3.

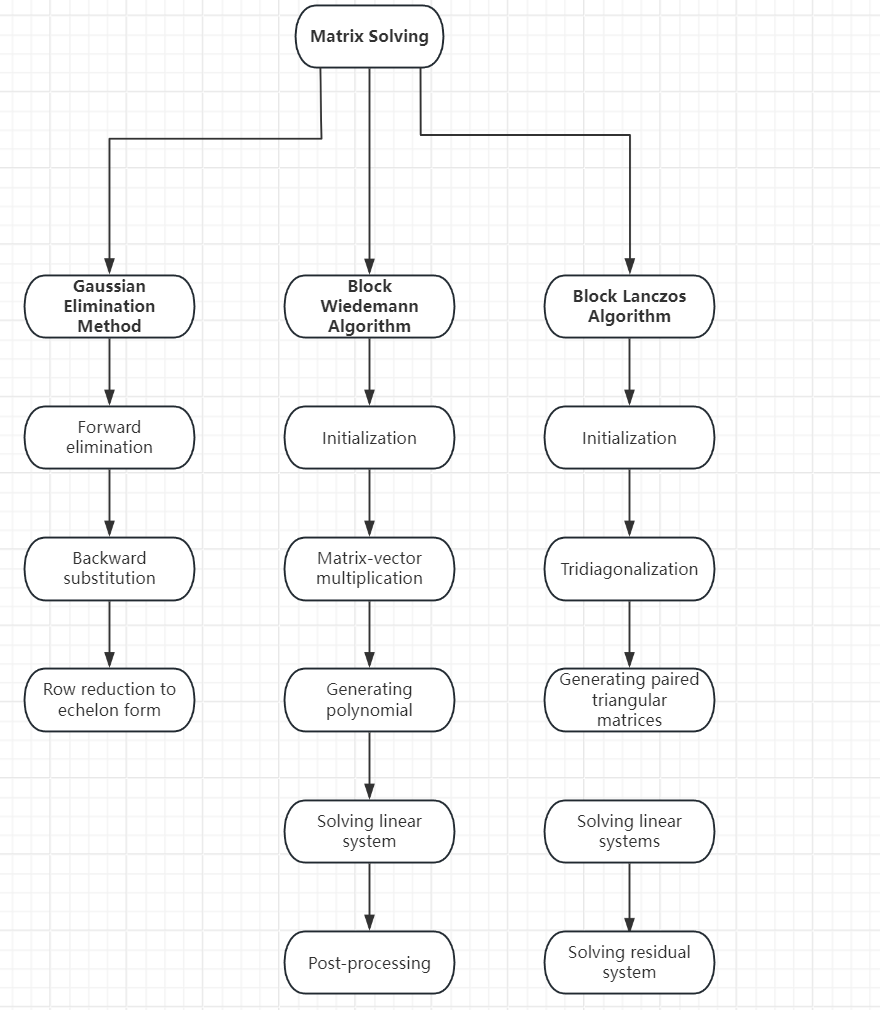
Figure 2. Three common methods of matrix solving (Photo credit: Original).

Figure 3. A new algorithm idea based on CRT (Photo credit: Original).

Since the Number Field Sieve (NFS) was proposed in 1988, it has continuously broken factorization records, setting one milestone after another in the factorization of large numbers [27]. From the successful factorization of RSA-100 in 1991 to the factorization of RSA-768 in 2009, NFS has demonstrated itself as one of the best algorithms for large integer factorization to date [28].

4. Future research directions and prospects

High Algorithmic Complexity: Will Simpler Algorithms Emerge? Currently, the NFS has the lowest complexity among large integer factorization algorithms, but it is also highly complex, involving multiple steps and a great deal of mathematical theory. Each step requires specialized knowledge and sophisticated algorithmic implementation. Whether there will be a more efficient algorithm with lower complexity is still an open question.

High Computational Resource Requirements and Large Memory Consumption. The NFS demands substantial computational resources, especially when factoring larger integers. Both the sieving and matrix-solving phases require significant computational power and memory. The high computational cost makes the NFS impractical for extremely large integers.

Inefficiency of the Sieving Stage. The relation collection (sieving) stage is the most resource-intensive part of the NFS, as it requires the collection of a large number of smooth numbers. Although this process can be parallelized, it still consumes a vast amount of computational time and resources, accounting for 90% of the total computation. Currently, there is limited research focused on improving the efficiency of the sieving process.

These issues highlight areas for potential improvement and further research to make the NFS more feasible and efficient for large-scale integer factorization tasks.

5. Conclusion

This paper provides a comprehensive review of the Number Field Sieve (NFS) algorithm, highlighting its critical role in the factorization of large integers, particularly within cryptographic applications like RSA encryption. The discussion encompasses the main components of NFS, including polynomial selection, number pair sieving, matrix solving, and square root extraction, each of which contributes to the overall efficiency of the algorithm. Recent advancements in NFS, such as improvements in polynomial selection techniques and optimizations in sieving and matrix-solving stages, have significantly enhanced the algorithm’s performance. The review also emphasizes the importance of NFS in cryptography, showcasing its effectiveness in breaking large integers and its superiority over other classical factorization methods. Looking ahead, the future research directions for NFS are centered on addressing its current limitations. One major challenge is the high computational resource requirement, especially in the sieving and matrix-solving stages, which account for the majority of the computational effort. Reducing the complexity and resource demands of these stages through innovative algorithms and enhanced parallel computing techniques is crucial for making NFS more practical for large-scale applications. Additionally, exploring new methods to simplify the overall structure of NFS could lead to the development of even more efficient algorithms with lower complexity. As computational capabilities continue to advance, further optimization and adaptation of NFS will play a vital role in the ongoing evolution of cryptographic security, driving the need for continuous research in large integer factorization methods.