1. Introduction

Tropical cyclones (TC) are powerful storm systems characterized through center pressure, emerging in tropical coastal regions, often accompanied with strong winds and heavy rainfalls [1]. Hurricanes, Typhoons are subordinate to TC according to the location of occurrence [2]. TC not only adversely affect maritime activities but also coastal areas like the Gulf of Mexico, and they could lead to catastrophic consequences from damage of infrastructures to loss of lives once cyclone makes landfall [2] [3]. As National and Oceanic Atmosphere and Administration (NOAA) stated, over the past six decades, more than 170 tropical storms, including over 60 hurricanes, have struck the Gulf coast, resulting in severe storm surges and extensive damage, often causing devastating floods [4] [5]. And therefore, it is imperative to accurately predict the locomotion of cyclones in order to prevent such outcomes

However, cyclone forecasting remains complicated attributed to chaotic atmospheric and oceanic interactions, making it a multi-aspect time-series task [6]. The uncertainty and potential severe impacts of inaccurate predictions further complicate this process compared to traditional forecasting. Conventional models like Numerical Weather Prediction (NWP) were widely used, however, it struggles with physical processes and the computational complexity which limits the accuracy [7]. To mitigate these challenges, Bayesian inference combined with Markov Chain Monte Carlo (MCMC) methods have been explored in geological and environmental contexts and could also assist with meteorological predictions [8]. And recently, deep learning advancements have improved cyclone prediction accuracy and reliability, with models like Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks illustrating abilities in accurately forecasting cyclone related events [6].

The project proposes a deep learning model that combines Convolution, Bidirectional-Long-Short-Term-Memory (Bi-LSTM), and traditional LSTM to predict tropical cyclone trajectory. The model will be used as a single model, with 6-dimension input and 2-dimension output. Performance evaluation includes statistical comparison and visualization of actual and predicted coordinates. Model parameters will be adjusted to balance computation quantity, efficiency, and accuracy.

The paper is organized as follow. Section 2 offers related previous works and methods, Section 3 presents the methodology applied to this project, including materials selection, Section 4 provides the experiments and results produced from the project and Section 5 discuss the formal results of proposed methods and conduct few fair comparisons with basic models. Finally, Section 6 concludes the work and deliver insights on possible future efforts.

2. Related Works

Kapoor et al. [6] proposed a cyclone trajectory and intensity prediction methods based on variational RNNs, which not only improves prediction accuracy but also quantifies uncertainty. Their approach utilizes Bayes-RNN and Bayes-LSTM models, and form the problem as a 3-dimensional time series, involving latitude, longitude and wind speed which displayed excellent performance throughout multiple ocean basins Pall et al. [8] developed Bayesreef, a Bayesian inference method designed specifically to adapt to respond to environmental changes in model coral reef development. This framework effectively quantifies uncertainty in stratigraphic models like pyReef-Core, thereby enabling precise predictions of reef dynamics across different environmental conditions. Bayesreef intelligently controls difficult parameters and produces accurate predictions by using past knowledge with observational data. Especially in addressing uncertainty and multidimensional difficulties, this approach provides ideas for improving the dependability and accuracy of cyclone prediction models.

As for deep learning methods, Lian et al. [9] introduced the AE-GRU model, which significantly improved trajectory accuracy across various time frames. Feng and Xu [10] developed a GRU-based model with a DILATE loss function, boosting storm surge prediction accuracy, especially for longer forecasts. Bose et al. [11] applied LSTM networks for North Atlantic hurricane predictions, achieving accuracy comparable to the National Hurricane Center with faster predictions. Sattar et al. [2] used a stacked ensemble model combining LSTM and GRU, reducing prediction errors and variance.

Two models developed by Qin et al. [12] improve typhoon and hurricane track forecasts. Strong RMSE performance allowed the DeepFR model—which combined BiLSTM and 3D CNN with multi-task learning—to greatly increase prediction accuracy. Particularly in capturing changing typhoon trajectories, the Trj-DMFMG model improved typhoon path prediction utilizing multimodal fusion and multi-task learning over conventional regression techniques.

Varalakshmi et al.[5] used Convolutional Neural Networks (CNN) and traditional machine learning classifiers to improve tropical cyclone prediction accuracy in the Indian coastal region. Their CNN model achieved 92.52% accuracy, further improved to 96.11% when combined with an enhanced C4.5 decision tree. Feng et al.[13] developed an innovative ED-ConvLSTM model for complex subsurface dynamics in geological carbon sequestration, outperforming traditional models like U-Net in prediction accuracy and computational efficiency. Both researches highlight the efficiency of CNNs and deep learning, so providing insightful analysis for the convolutional layers in suggested model.

3. Methodology

1.1 Dataset

This project uses the HURDAT2 dataset, an enhanced version of the original HURDAT database, to study tropical and subtropical cyclones in the Atlantic basin. The updated version includes more precise information and observations, addressing shortcomings in the original dataset. The dataset, a CSV file covering 1851 to 2020, contains 52,718 records representing over 1,900 unique cyclones. It includes basic track information, maximum sustained wind speeds, minimum central pressure, landfall indicators, and cyclone status at various stages. The dataset is organized for modeling, forecasting, and retrospective analysis, with each storm's record starting with a header providing essential details. The subsequent entries provide chronological information on the storm's position, intensity, wind radii, and other critical factors at specific time intervals.

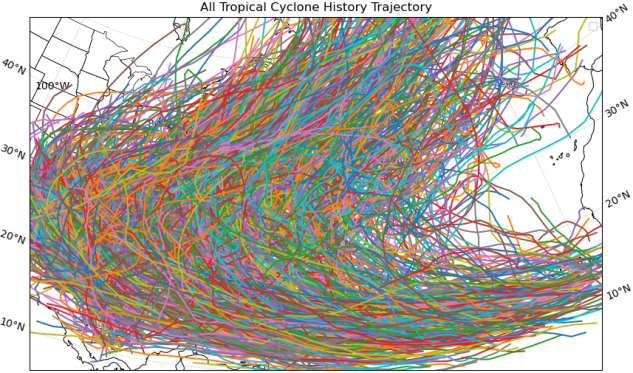
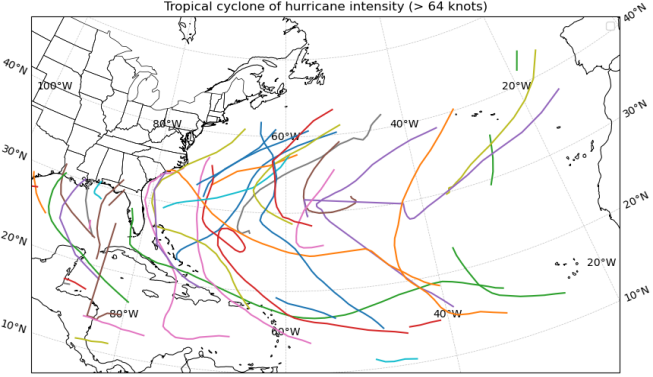
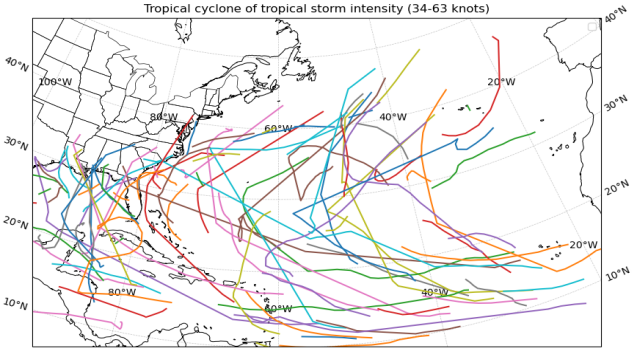
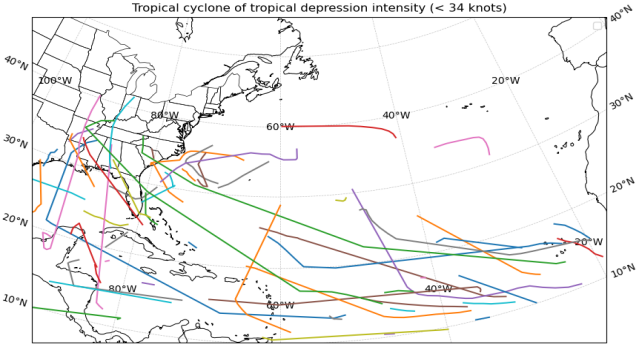
HURDAT2 has been continuously updated to incorporate the latest scientific insights and observational capabilities, making it a dynamic resource essential for tropical cyclone study. However, due to technological limitations, the reliability of the data, particularly regarding central pressure and wind radius, is lower, resulting in a significant amount of missing data. Therefore, data processing steps were necessary to ensure the project's objectives could be met. Fig. 1 represents the examples of cyclones.

1.2 Dataset processing

The project aimed to predict cyclones by analyzing data related to latitude and longitude. However, over 39,000 rows had missing data for minimum cyclone center pressure and influence radius, likely due to technical constraints. These columns were excluded from the analysis, and the remaining features like years, months, days, hours, latitude, and longitude were directly related to shifts in latitude and longitude. The data of hours was recorded at 6-hour intervals throughout each day. Examples of the retained features are presented in Table 1.

Table 1: Data feature examples

The model uses features from Table 1 to form features matrix for training, then predicting latitude and longitude coordinates from cyclone trajectory data. The data is structured into sequences of 5 consecutive time steps, allowing for more accurate predictions. The data is split into train, validation, and test datasets with a 70%:15%:15% ratio, and normalized using MinMaxScaler. The data process pipeline is illustrated in Fig. 2.

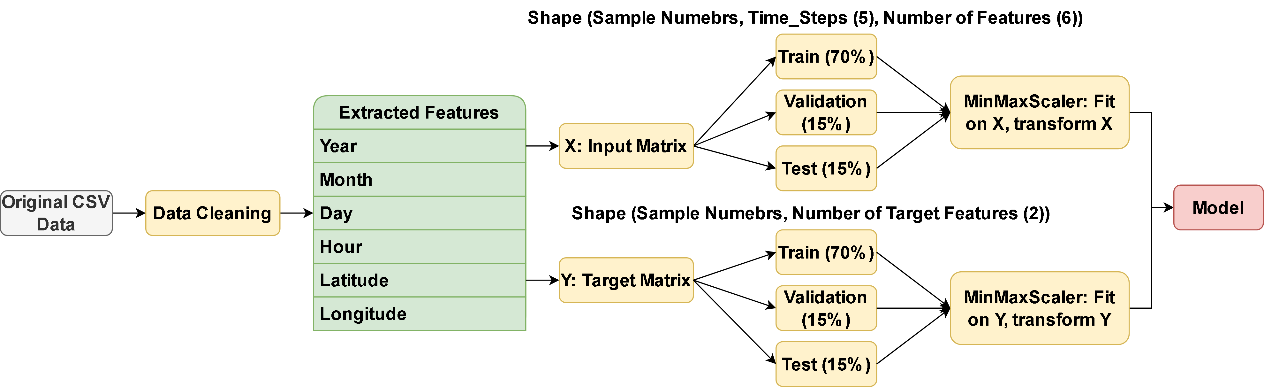
Fig. 2: Data Processing and Preparation Pipeline

1.3 Recurrent Neural Network (RNN) & Long-Short-Term Memory (LSTM)

Model is constructed based on LSTM structure, which has the effectiveness on addressing the explosion or vanishing of gradient problem that conventional RNNs [10]. In standard RNNs, gradients can diminish exponentially during backpropagation and obstructs the learning of long-term dependencies, which is crucial for tasks like cyclone trajectory prediction that rely on historical data [14]. LSTM, a specialized RNN variant, overcomes this by using input, forget, and output gates to maintain essential information over time while preventing gradient vanishing and explosion issues [6]. The basic structure of a LSTM neuron is demonstrated in Fig. 3.

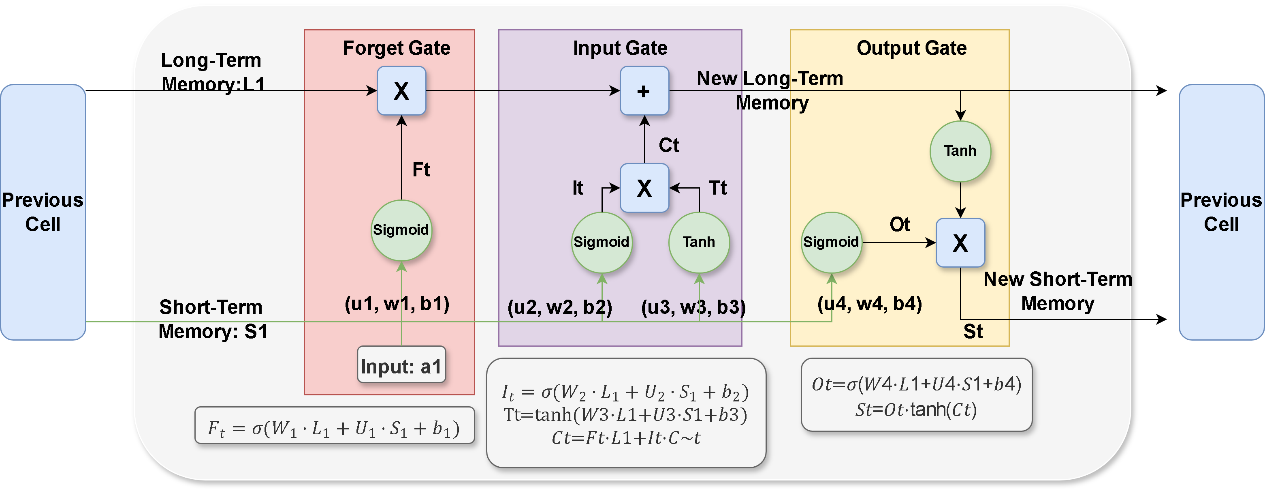
Fig. 3: LSTM Single Cell

1.4 Bidirectional Long-Short-Term Memory (Bi-LSTM)

To improve tropical cyclone trajectory predictions, Bi-LSTM layers are employed. Bidirectional Long-Short-Term Memory enhances traditional LSTM by processing data in both forward and backward directions, capturing dependencies from both past and future contexts more effectively [14] [15]. Bi-LSTM uses two LSTM networks, one reading data forward and the other in reverse, providing a richer feature representation and a more comprehensive understanding of the sequence, which enhances trajectory prediction capabilities [15]. Fig. 4 represents the Bi-LSTM structure.

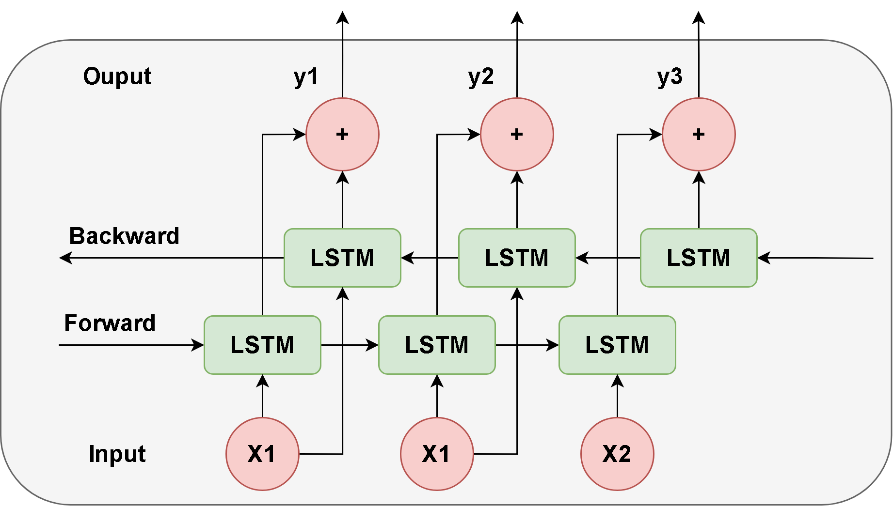
Fig. 4: Bi-LSTM basic structure

1.5 Convolutional Layer

The Convolutional Layer is key in deep learning models, designed to learn hierarchical features from input data. It applies filters (kernels) across the data to perform element-wise multiplication and summation, producing feature maps [16]. The depth of the layer determines how well these maps capture fundamental patterns like edges, textures, and more abstract representations in the data. Fig. 5 demonstrates the basic logic of convolutional layer of one dimension.

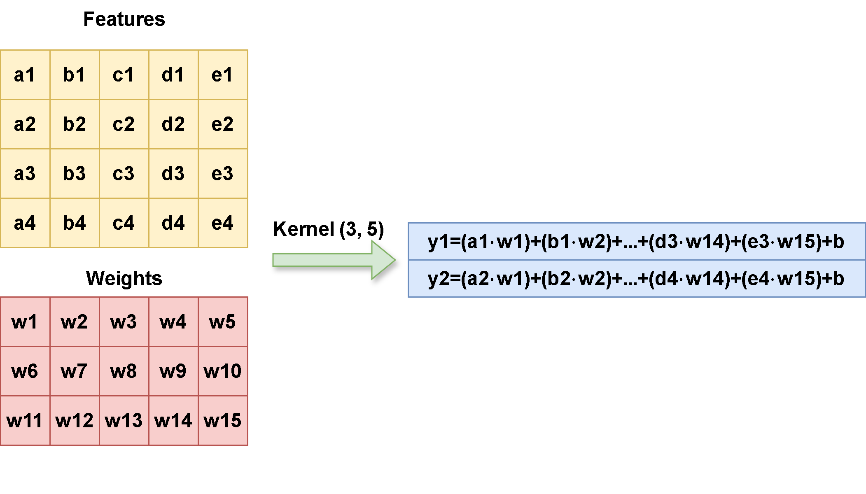
Fig. 5: Convolutional Layer Logic of One Dimension

1.6 Proposed Model Architecture

The proposed model uses a complex structure with a small number of parameters, starting with a 64-unit convolutional layer for local patterns and MaxPooling1D for reducing dimensions. Data is processed through Bi-LSTM layers, batch normalization, dropout layer, and traditional LSTM layers. A dense layer outputs predicted coordinates, balancing complexity and performance. This model is suitable for trajectory prediction with simple data processing without feature generation, making it suitable for time series data processing. Proposed model structure is displayed in Fig. 7, where training and prediction are completed through the process within it, Mean Squared Error (MSE) serves as the loss function.

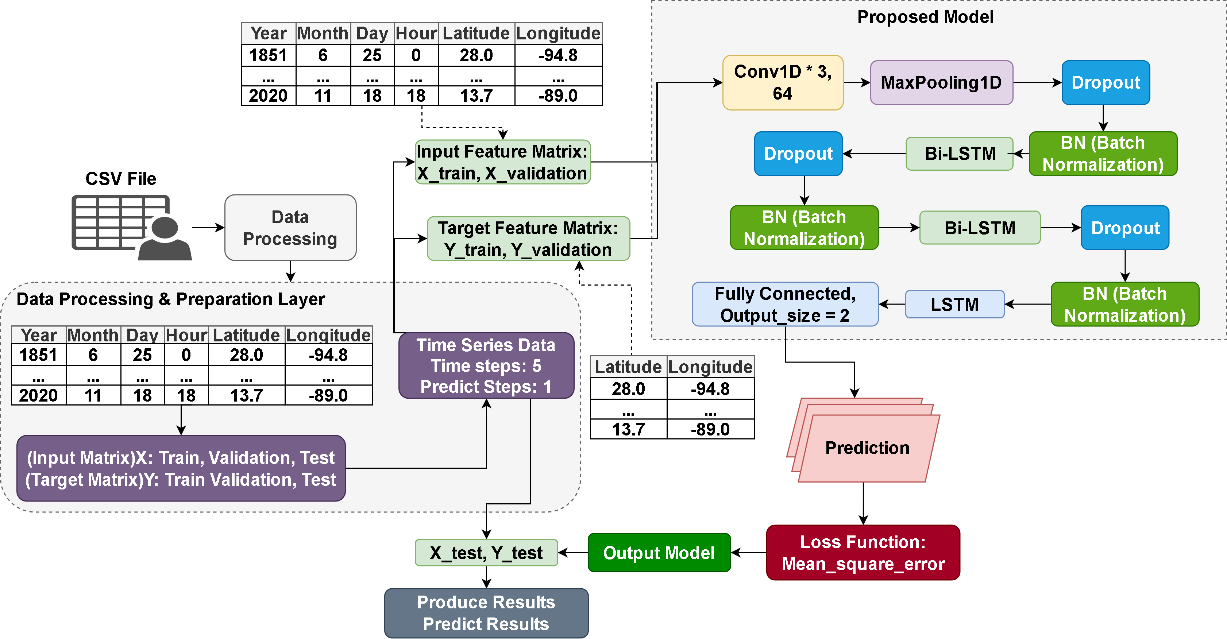
Fig. 6: Proposed Model and Pipeline of Training and Prediction

4. Experiment and Results

4.1 Fine Tune with Hyperparameters

This section displays the fine-tuning experiments and results, including optimizers, learning rate, batch size, and model with and without convolutional layers. Evaluation are metrics of loss, MSE, MAE and RMSE. All experiments incorporate early stopping.

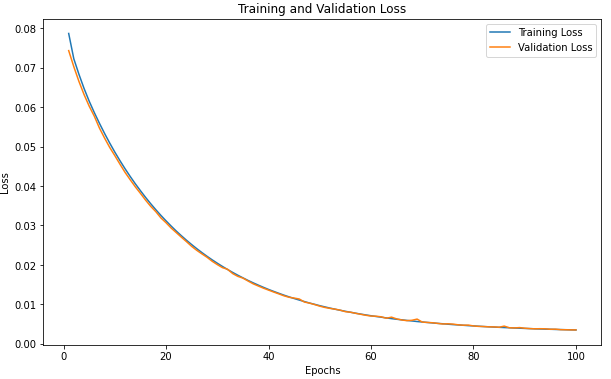
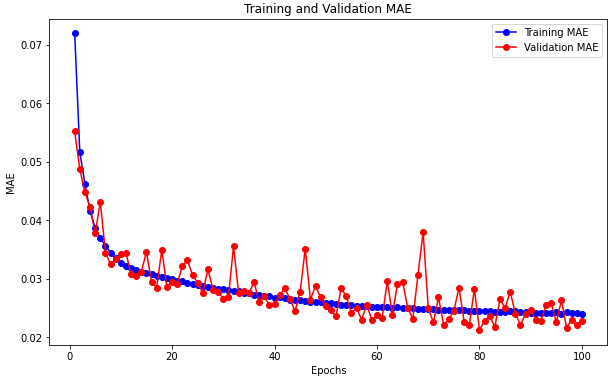
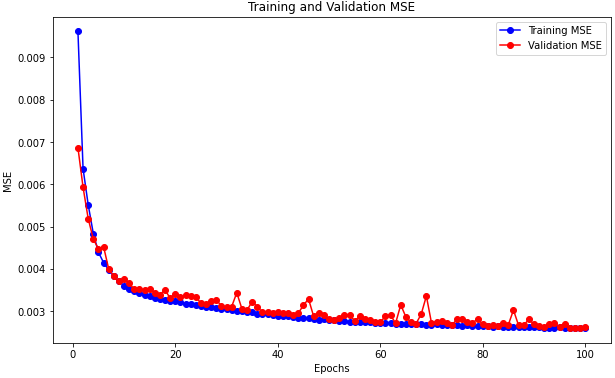
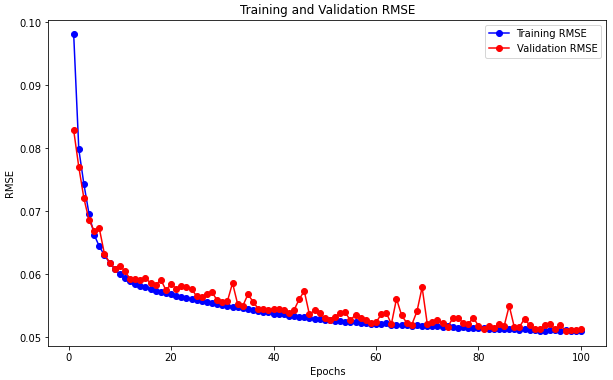
Starting with the initial model without convolutional layers, the results (Loss, MSE, RMSE, MAE) are shown in Fig. 8. The initial model showed stable fitting with a validation loss of 0.0035 under MinMaxScaler normalization. However, other metrics, particularly MAE, fluctuated significantly during training, likely due to the model’s difficulty in capturing complex feature relationships within the data. While the metrics were generally good, there is room for hyperparameter optimization to achieve a more stable model and improve trajectory prediction accuracy.

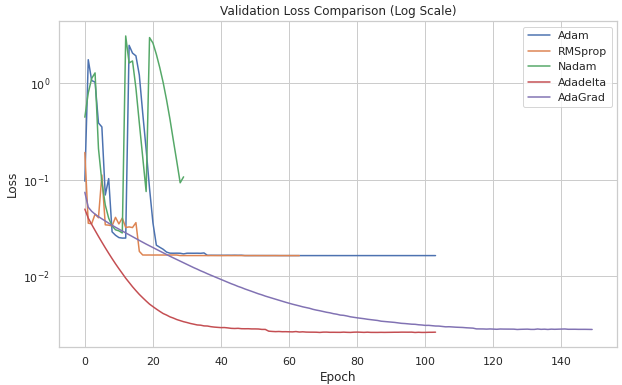
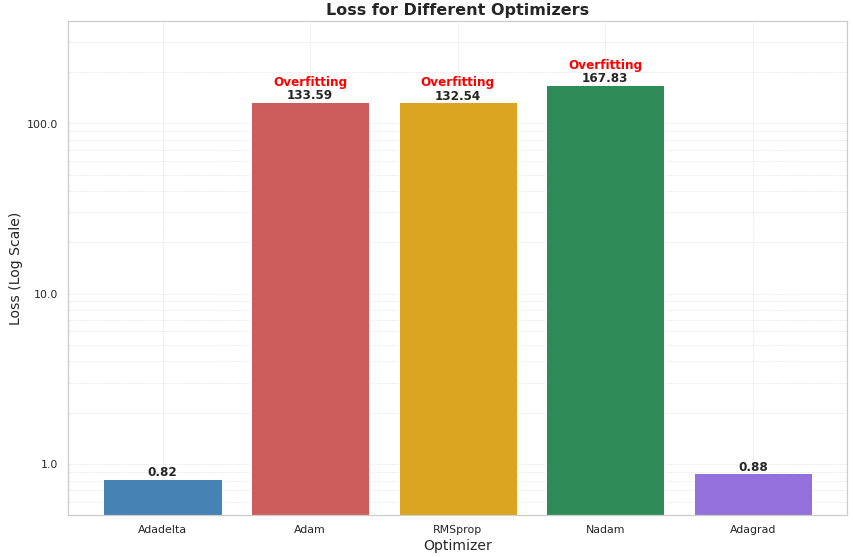
Fig. 9 compares the validation and test loss across five optimizers: RMSprop, Adam, Nadam, Adadelta, and Adagrad. RMSprop effectively maintains a steady learning rate, particularly useful for recurrent structures [17]. Adam, combining momentum and RMSprop, adjusts the learning rate dynamically for sparse gradients and noisy data [18]. Nadam enhances Adam by integrating Nesterov-accelerated gradients for faster convergence [17]. Adagrad adapts the learning rate based on accumulated gradients, while Adadelta refines this by limiting the accumulation to prevent diminishing learning rates [17]. The comparison of optimizers revealed significant differences in performance. Adadelta and Adagrad showed the lowest losses (0.82 and 0.86) on specific trajectory, indicating their effectiveness in predicting irregular and chaotic trajectory data. However, RMSprop, Adam, and Nadam all displayed signs of overfitting. These optimizers struggled with unconventional data, with Nadam exhibiting erratic fluctuations in validation loss curves. Based on convergence and losses, Adadelta was chosen as the optimal optimizer, as it effectively managed the data without overfitting.

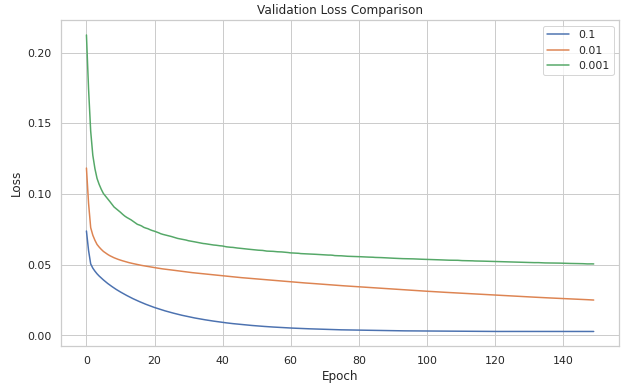
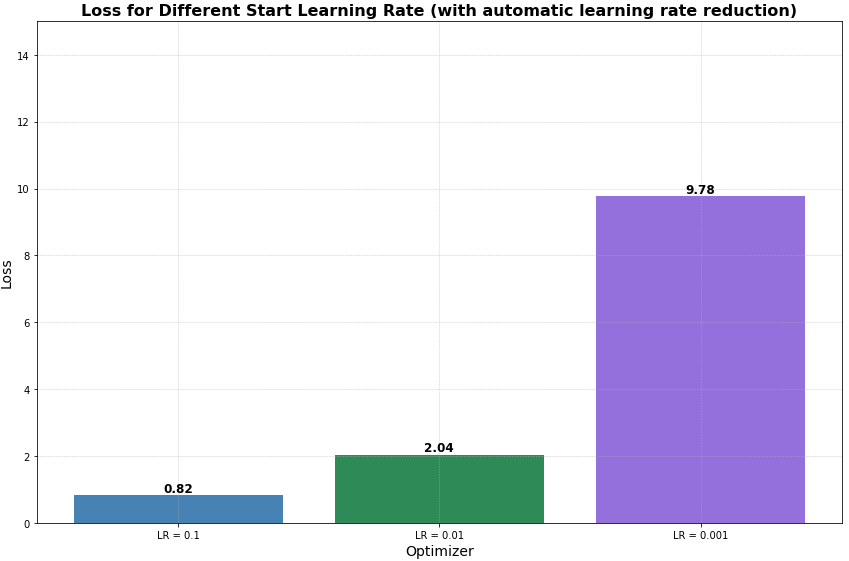
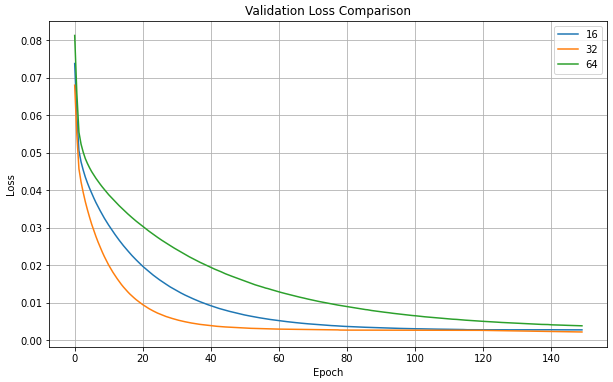
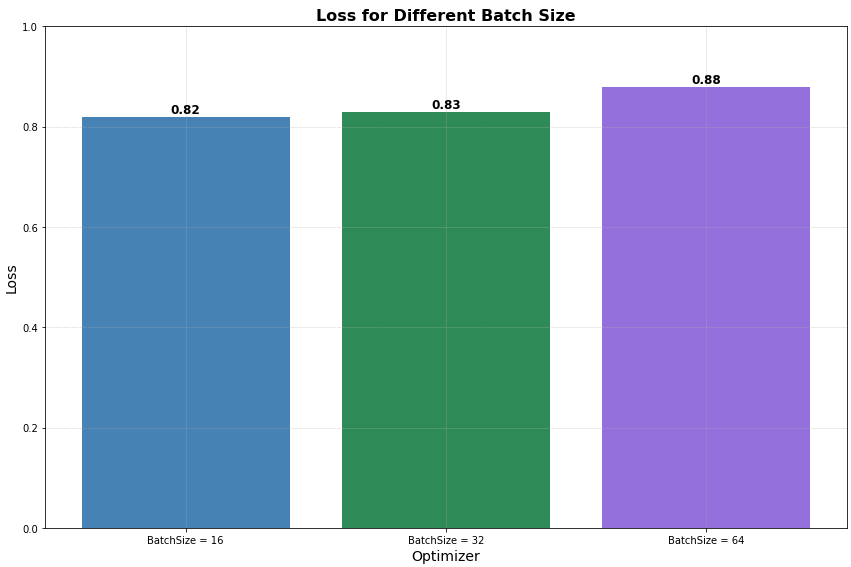
Fig. 10 presents the impact of different learning rates and batch sizes on model performance. As shown in Fig. 10 a) and 10 b), a higher learning rate of 0.1 led to the best convergence and the lowest MSE of 0.82 for trajectory prediction, indicating effective avoidance of local optima. Conversely, the lowest learning rate increased MSE, suggesting a risk of getting stuck in suboptimal solutions. Fig. 10 c) and 10 d) demonstrate that a batch size of 32 achieved the best MSE and validation loss, striking an optimal balance between gradient noise and model stability. This batch size helped the model avoid excessive noise from smaller batches and overly smooth gradients from larger ones, leading to better generalization. Consequently, subsequent experiments used the Adadelta optimizer, a learning rate of 0.1, and a batch size of 32.

4.2 Model with Convolutional Layer

The model was stabilized and further improvements were made to improve trajectory predictions by integrating convolutional mechanisms and adjusting the layer structure. The initial model and the first modified model showed similar trends in validation losses, dropping rapidly at early stages and stabilizing later. The proposed model and Modified-3-model demonstrated faster and more stable descent of losses with the replacement or reduction of Bi-LSTM layer, eventually convergent to a loss close to the original one. Structural changes caused these results, such as replacing one Bi-LSTM layer with a conventional one, reducing computations in both directions, and decreasing complexity. The modified-3-model simplified the model structure, supporting this notion. However, the average MSE of the modified-3-model was higher than the proposed model, suggesting that the model may have left less complexity. The proposed model found a balance between layer diversity, model complexity, and prediction accuracy.

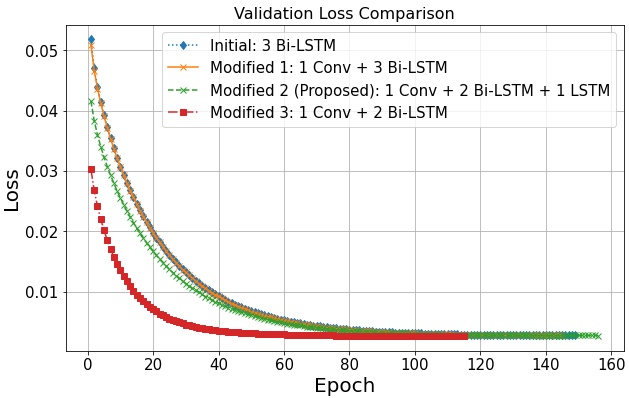
Fig. 10: Comparison of Initial Model and Modified model Training Loss

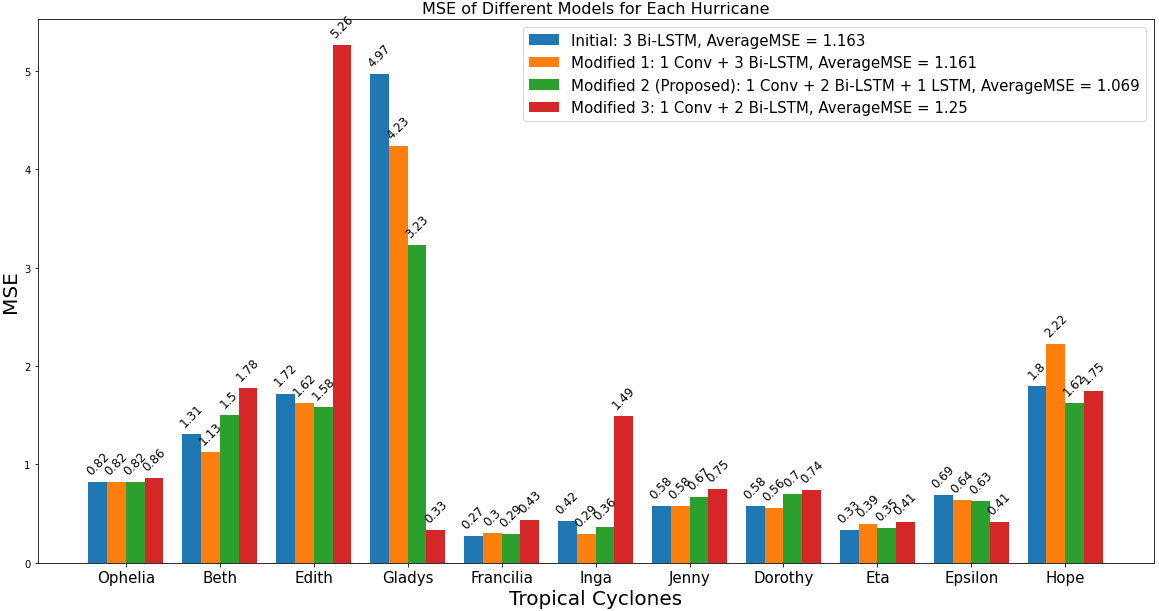
Fig. 11: Comparison on 11 Different Cyclone Trajectories using Initial Model and Three Improved Model with Convolutional Layers

Table 2 illustrates the summary of results produced by initial model, proposed model and basic models which will be discussed with proposed model in discussion section.

Table 2: Results Summary of Initial Models, Proposed Models, GRU, LSTM, and RNN

5. Discussion

For sequential data prediction, such as language models or time sequence prediction, Recurrent Neural Networks (RNNs) are often the solution. In cyclone trajectory prediction, where features from previous events are crucial, RNNs are effective. As for LSTM, a specialized RNN, was developed to address issues like gradient vanishing or explosion, making it suitable for tasks that require retaining information from longer sequences [11]. Even though with the theoretical foundation, the results of basic RNN and LSTM cyclone trajectory are unknown, since cyclone possess unconventional patterns and chaotic in nature [12]. Furthermore, Gate Recurrent Unit (GRU), one of the derivatives of RNNs widely used, sometimes can be more effective than traditional RNN on long-term dependencies [19]. With these notions, the following comparison was conducted and the validation losses are presented in Fig. 14, and the MSE of four different models tested on 11 different cyclone trajectories are illustrated in Fig. 15.

The validation loss curve reveals each model's statistical performance based on learned patterns from the dataset. Basic RNN, LSTM, and GRU showed relatively fast convergence due to their simpler architectures and consistent structures, which led to lower variance and reduced parameters. GRU, with only one update and reset gate, is more efficient but less complex, limiting its ability to learn intricate patterns [9] [20]. In contrast, the proposed model with a more complicated structure that includes convolutional, Bi-LSTM, and LSTM layers, while it is aim at capture features and patterns at various scales it relatively increases the complexity. This also ensures the preservation of long and short-term memory, reducing the risk of losing crucial information. Fig. 15 demonstrates that, apart from Gladys’s trajectory, the proposed model performs consistently well across other paths, with no significant anomalies, indicating its stability compared to the rest three models.

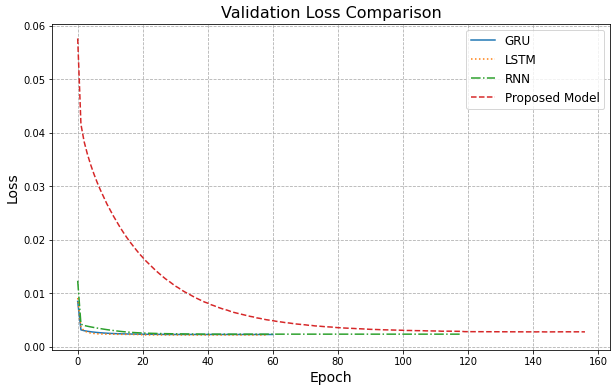
Fig. 12: Comparison of Validation Losses on Four Different Models

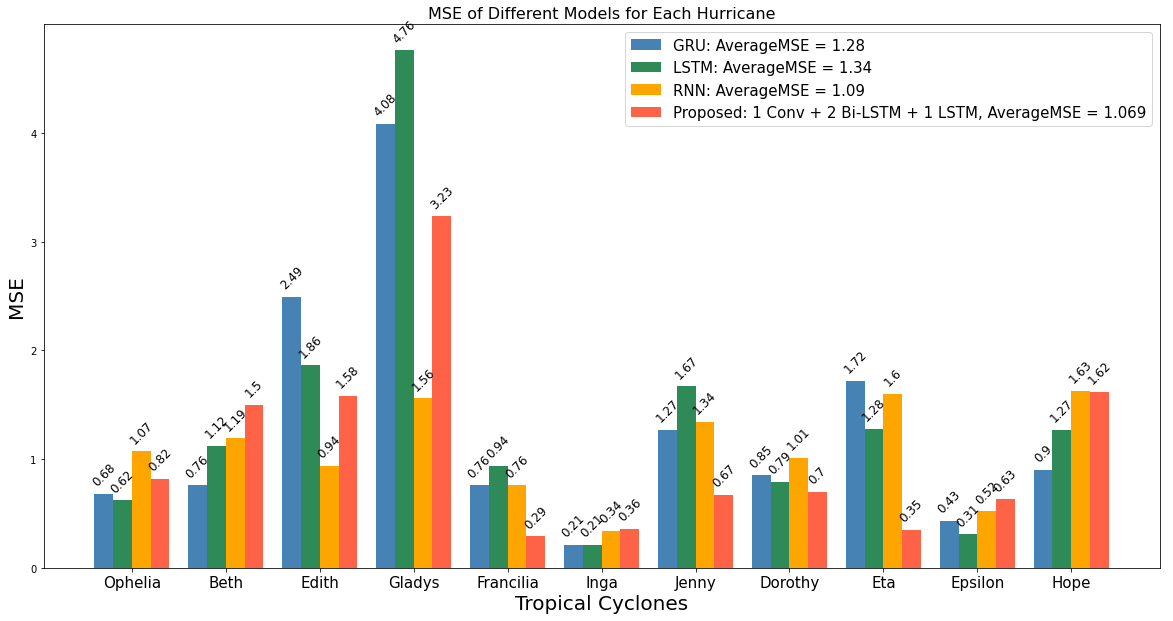
Fig. 13: MSE of Four Different Models Predicting 11 Different Cyclones

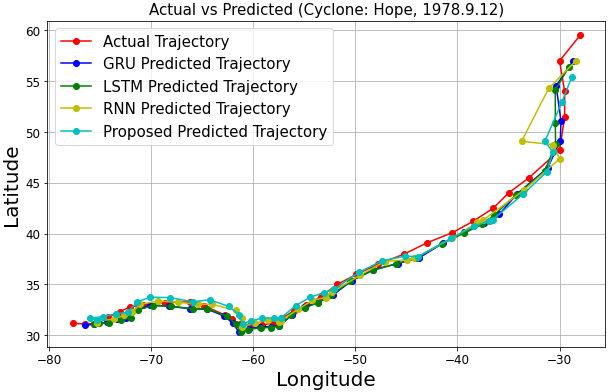
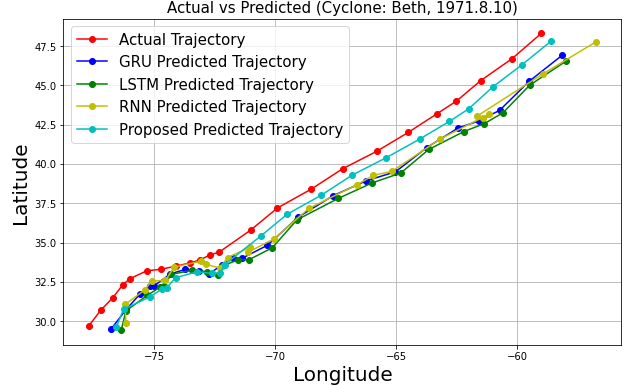
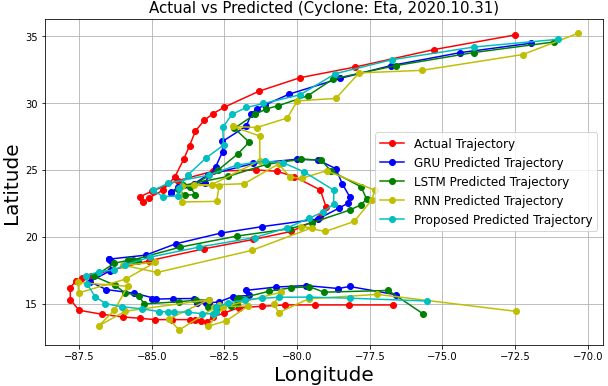
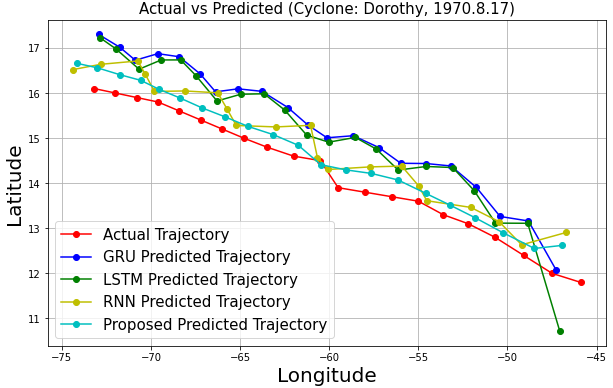
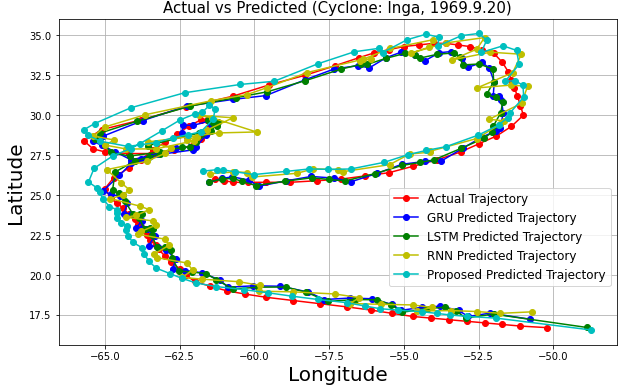
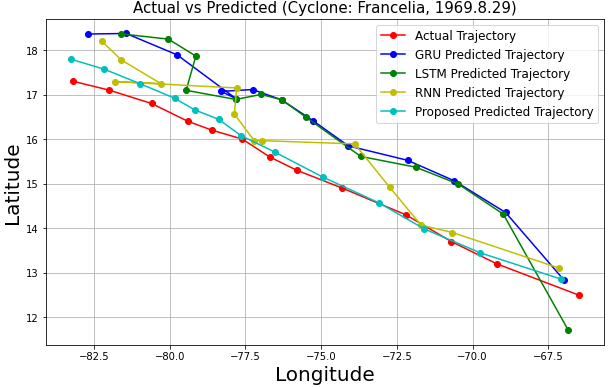
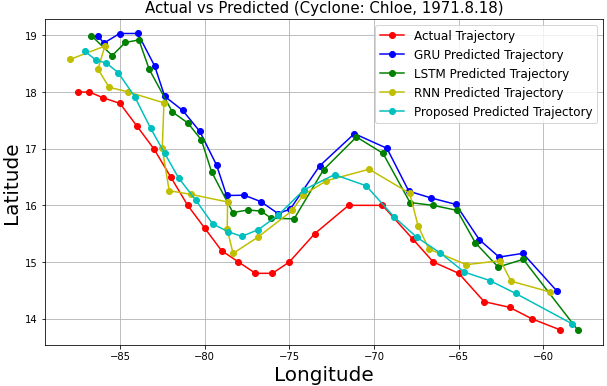
As shown in Fig. 16, the predicted trajectories are generally close to the actual coordinates, demonstrating effectiveness and stability across models. However, RNN, LSTM, and GRU showed severe fluctuations and inaccuracies, particularly at wide turns for cyclones like Eta, Dorothy, Francelia, and Inga, likely due to their simplistic structures and limitations in capturing complex patterns [21].

In contrast, the proposed model provided more accurate and stable predictions, attributed to the integration of convolutional layers with Bi-LSTM networks. These layers effectively capture spatial and temporal dependencies, enhancing dynamic prediction performance [13].

The proposed model is more accurate in predicting cyclone Dorothy and Francelia's shorter trajectory, but may have lower reliability compared to other models due to the limited number of reference coordinates. This is also true for cyclone Chloe, as frequent turning points limit the number of coordinates that can be formed into a sequence long enough for each model to predict the next coordinate, limiting the accuracy of the prediction.

6. Conclusion and Future Work

This project presented an HURDAT2 dataset-based Conv-Bi-LSTM model for TC trajectory prediction. With real and anticipated trajectories plotted for further analytics, the performance of model was assessed against conventional models like RNN, LSTM, and GRU. Proposed model had shown better relatively better capabilities in managing complex patterns and transitions especially. Though its strength is in holding information over longer sequences, hence making it resilient for trajectory prediction, increased computation complexity might lead to lower convergence speed than GRU, LSTM, and RNN.

The chaotic nature of cyclone trajectories makes it difficult to anticipate the exact coordinates with simpler models. The time series character of the data required deliberate model construction and parameter tuning. Achieving an ideal predictive performance, the suggested model effectively balance the depth of layers with the number of neurons. However, some limitations were noticeable, such as sensitivity to data volume and the difficulty in significantly narrowing the latitude and longitude prediction errors with relatively fewer features.

Future research should concentrate on following aspects, leveraging current data to create new features could improve prediction performance. For instance, calculating the movement speed towards a specific direction based on hourly shifts of latitude and longitude, or identifying trends from changes in wind speed which may provide additional relevant features. Furthermore, through current model employs various layers for diverse feature learning, its complexity is constrained. The model complexity should be enhanced as the correlations among features increase. Additionally, it might not be sufficient for high accurate predictions solely relying on deep learning models, and therefore, more exploration towards the integration of multiple models based on different conceptual frameworks are anticipated.