1. Introduction

With the development of sensor technology and artificial intelligence, robots have been widely used in industrial production, extreme environment exploration, and healthcare [1].

Robotic arms are subject to dynamics and kinematics constraints in performing motion operations from one point to another as a result of their geometry (linkage length and joint type), and also the coupled nature of multiple degrees of freedom (DOF) can make it difficult for the arm to accurately follow predetermined paths and attitudes [2]. The path planning problem of a robotic arm can basically be thought of as moving from a start point to a goal point without collisions on the way. Existing path planning methods can be broadly classified into three main categories: Heuristic Algorithms, Sampling-based Algorithms, and Machine Learning.

1.1. Heuristic Algorithms

Since the types of heuristic algorithms are too heterogeneous, both the artificial potential field method and the meta-heuristic algorithm are considered here as heuristic algorithms.

Heuristic Algorithms use some heuristic information to improve the search efficiency. This kind of algorithm is the most varied of such algorithms, the typical ones are the A* algorithm, Dijkstra's algorithm and artificial potential field (APF) method [3], [4]. In addition, there are many meta-heuristic algorithms such as Particle Swarm Optimisation (PSO) [5] and Genetic Algorithm (GA) [6].

1.2. Sampling-based Algorithms

Sampling-based motion planning algorithms are one of the most valuable algorithms in robot motion planning because they can efficiently plan paths in complex environments. Among such algorithms, Probabilistic Roadmap (PRM) [7], [8] and Rapidly Exploring Random Trees (RRT) [9] are two of the more established algorithms.

1.3. Machine Learning

Traditional algorithms have achieved compelling results in path planning, but they have long computation times in dynamic environments, which can lead to unstable computation of optimal solutions. And in recent years, machine learning has gained attention and applications because it can solve complex motion path problems well [10], and the main directions are deep learning and reinforcement learning [11], [12]. This approach allows the use of data to reduce or even eliminate the reliance on complex models and make path planning methods simpler [13].

1.4. Limitations of Individual Algorithms

Individual algorithms are often difficult to overcome drawbacks. For example, the APF algorithm suffers from Goal Nonreachable with Obstacles Nearby (GNRON) and local optimality [14], and RRT converges slowly and does not guarantee path optimality [15]. Therefore, using another algorithm to compensate for the defects of one algorithm becomes an important way to improve the algorithm. On the other hand, with the development of artificial intelligence, many machine learning-based methods have been used to optimize the path planning of robotic arms [16], [17], such as deep learning [18] and reinforcement learning [19].

While research on robotic arm path planning has made significant strides, there is a lack of comprehensive reviews that systematically summarise hybrid algorithms. This paper will discuss the methods of combining multiple algorithms to optimize the path of a robotic arm, the next section will explain the methodology of literature screening and the criteria of literature classification, the third section will discuss the innovations and basics of each hybrid algorithm, and the fourth section will discuss the research gaps and future directions of the hybrid algorithms for controlling robotic arms.

This essay focuses on two questions:

• Q1: What are the combinations of hybrid algorithms for robotic arm path planning?

• Q2: What problems are solved by hybrid algorithms for robotic arm path planning?

2. Literature Collection

A range of authoritative and representative databases were selected for this review, such as Google Scholar, ScienceDirect and Edinburgh Napier University Library. In this paper, 58 articles were initially selected from 2010 to 2024, and 18 articles were screened to meet the requirements.

In the search process, the first batch of documents were obtained with the core keywords ‘robotic arm’ and ‘path planning’, and then the abstracts of these documents were checked for algorithmic elements, and excluded if there were none. The next step is to read whether these papers are designed to improve the algorithms or combine with other algorithms, and exclude if there were none. Finally, the screened literature was categorised. In addition, to ensure the comprehensiveness of the retrieved literature, synonyms of keywords were considered, such as ‘deep learning’, ‘artificial intelligence’, ‘RRT’, ‘heuristic’.

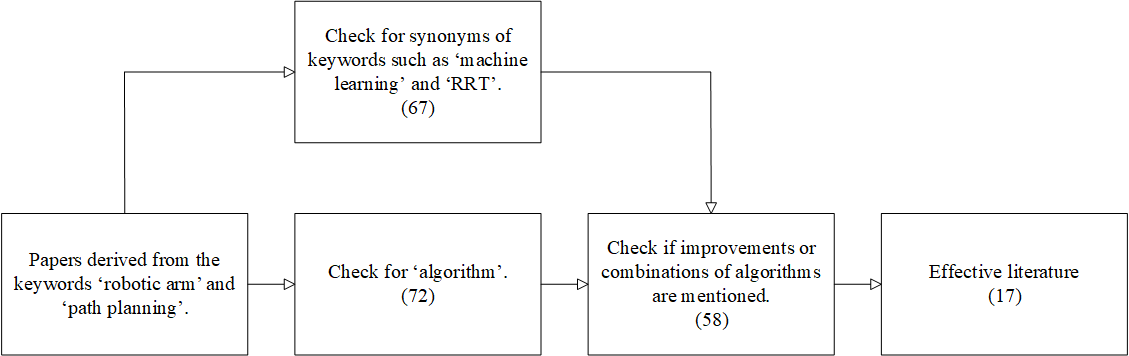
Figure 1: Inclusion Criteria

3. Review of the Literature

This section provides answers to the questions in the introduction.

3.1. The combinations of hybrid algorithms

In this paper, the retrieved hybrid algorithms are categorised into three types of algorithms according to their combination: heuristic algorithm + heuristic algorithm, heuristic algorithm + sampling-based algorithm, and traditional algorithm + machine learning.

3.1.1. Heuristic Algorithm + Heuristic Algorithm

This category is the most numerous, containing 8 papers. The algorithms involved are:

• Genetic Algorithm (GA) + Particle Swarm Optimisation (PSO) [20]

• Particle Swarm Optimisation (PSO) + D* algorithm [21]

• Particle Swarm Optimisation (PSO) + Simulated Annealing Algorithm (SAA) [22]

• Improved Whale Optimisation Algorithm (IWOA) + Particle Swarm Optimisation (PSO) [23]

• Simulated Annealing (SA) + Electro Search Simulated Annealing (ESSA) [24]

• Artificial potential field (APF) + A* algorithm [25], [26]

• Dingo Optimization Algorithm (DOA) + Simulated Annealing Algorithm (SAA) [27]

Heuristic Algorithm + Heuristic Algorithm is the simplest type of combination, and it is usually possible to combine the advantages of two different algorithms to further improve the search efficiency. Among the algorithms mentioned above the IWOA-PSO algorithm proposed by Zhao Jing and Zhu Xijing et al. is more typical. Firstly, the total population is randomly divided into two sub-populations S1 and S2, which are optimised and updated using IWOA and PSO respectively, and after sorting according to the fitness, 50% of the individuals from each sub-population are merged into a new sub-population S3, which is exchanged by the crossover strategy, and then the crossover individuals are assigned back to S1 and S2 randomly to keep the size of the sub-populations unchanged. After that, the individual fitness is calculated and the global optimal solution is updated to determine whether the termination condition is satisfied, and if not, the optimisation is repeated to output the global optimal solution. This hybrid optimisation algorithm improves the optimisation performance through sub-population division optimisation, cross-organisation and information sharing [23]. The structure of this hybrid algorithm is shown in Fig. 2.

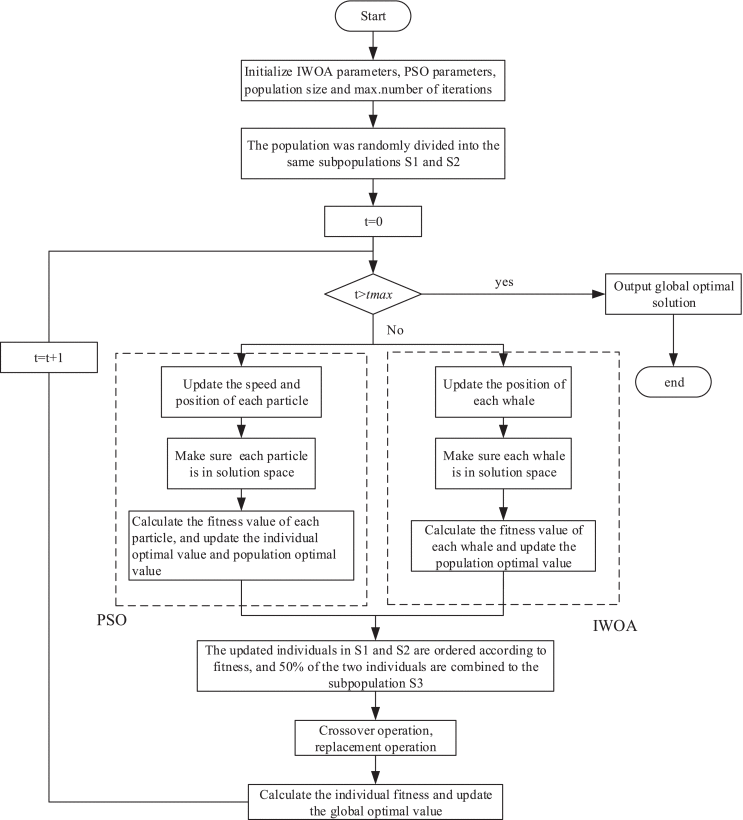
Figure 2: Structure of the IWOA-PSO algorithm [23]

3.1.2. Heuristic Algorithm + Sampling-based Algorithm

This category contains 4 papers. The algorithms involved are:

• Rapidly Exploring Random Tree (RRT) + Artificial Potential Field (APF) [28], [29], [30]

• Rapidly Exploring Random Tree (RRT) + Greedy Algorithm [31]

The heuristic algorithm + sampling-based algorithm introduces a sampling-based algorithm for the heuristic algorithm, which is better able to adapt to complex spaces and allows for real-time planning. Among the algorithms mentioned above the APF-RRT algorithm proposed by Yuan Qingni and Yi Junhui et al. is more typical. Firstly initialise the parameters, including obstacle environment, starting point, target point, step length and sampling rate. Then judge the distance between the current node and the nearest obstacle, if the distance is greater than twice the step size, then use the I-APF method for searching and advancing, calculate the gravitational force and repulsive force, and escape from local minima by using heuristic method. If the distance is less than twice the step size, the path search is performed using the I-RRT algorithm, which includes steps such as random sampling, nearest neighbour node selection, node expansion and collision detection. Finally, the obtained path is processed and judged whether it reaches the target point or not, if yes, the path is output, otherwise the optimisation continues iteratively. The algorithm makes full use of the advantages of I-APF and I-RRT and improves the global search ability while ensuring the path smoothness and obstacle avoidance, and can find the better collision-immune paths in complex environments [28]. The structure of the hybrid algorithm is shown in Fig. 3.

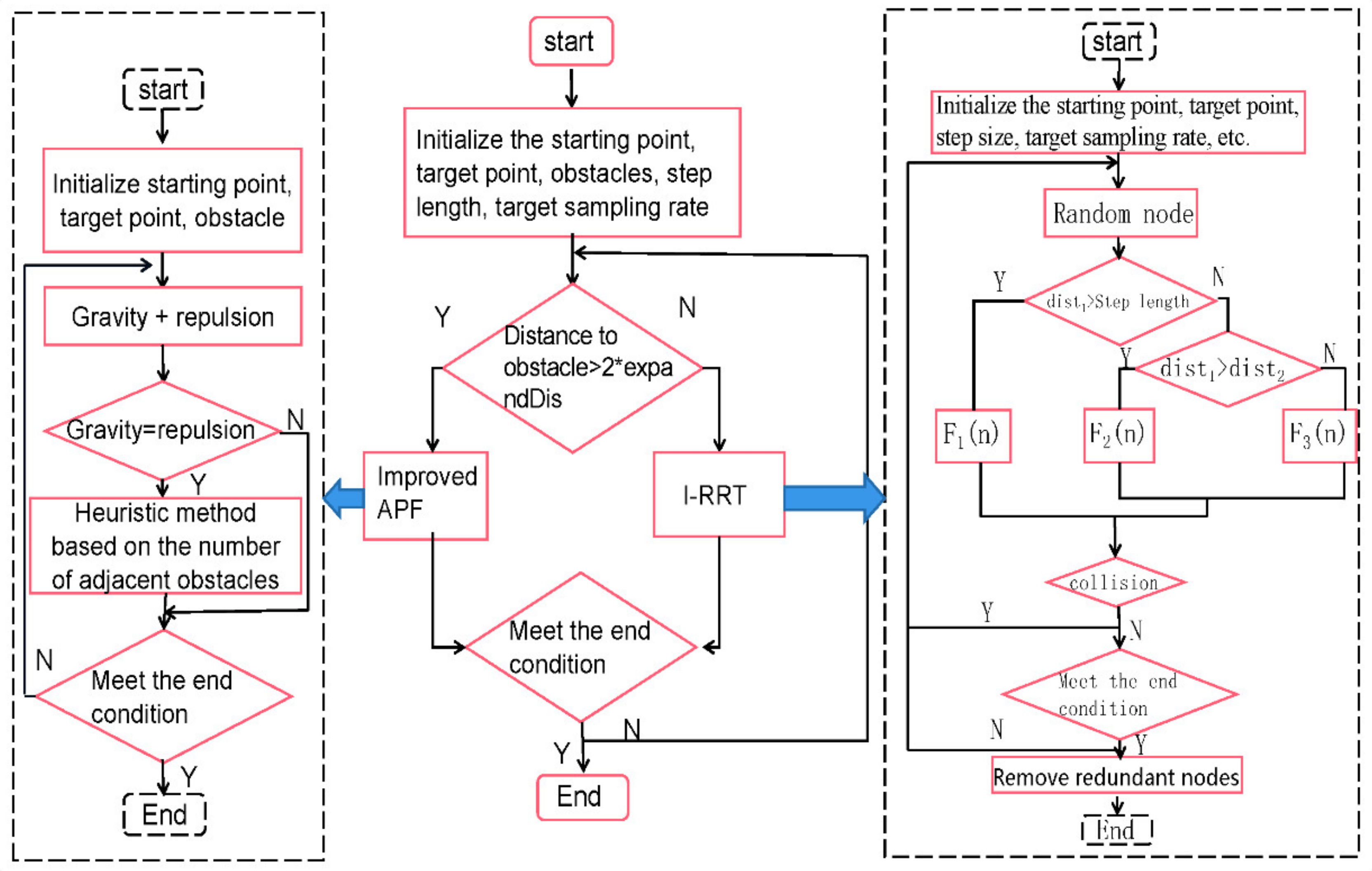
Figure 3: Structure of the APF-RRT algorithm [28]

3.1.3. Traditional Algorithm + Machine Learning

This category contains 3 papers. The algorithms involved are:

• Genetic Algorithm (GA) + Neural Network (NN) [32]

• Rapidly Exploring Random Tree (RRT) + BP Neural Network (BPNN) [33]

• Rapidly Exploring Random Tree (RRT) + Radial Basis Function (RBF) Neural Networks [34]

Traditional Algorithm + Machine Learning is a method that introduces machine learning for several of the above algorithms. It can learn better path planning strategies in complex environments and run efficiently but requires a lot of training data. Among the algorithms mentioned above the RRT-BPNN algorithm proposed by Yuan Qingni and Yi Junhui et al. is more typical. Firstly, initialise the map parameters and divide the space, calculate the sampling probability of each sampling space and predict the number of sampling nodes in each stage using BP neural network. In the first stage, new nodes are generated by nearest neighbour node expansion and collision avoidance; in the second and third stages, the sampling probability and roulette method are combined to select the sampling space for node generation until the target point is reached and a collision-free path is planned [33]. The structure of the algorithm is shown in Fig. 4.

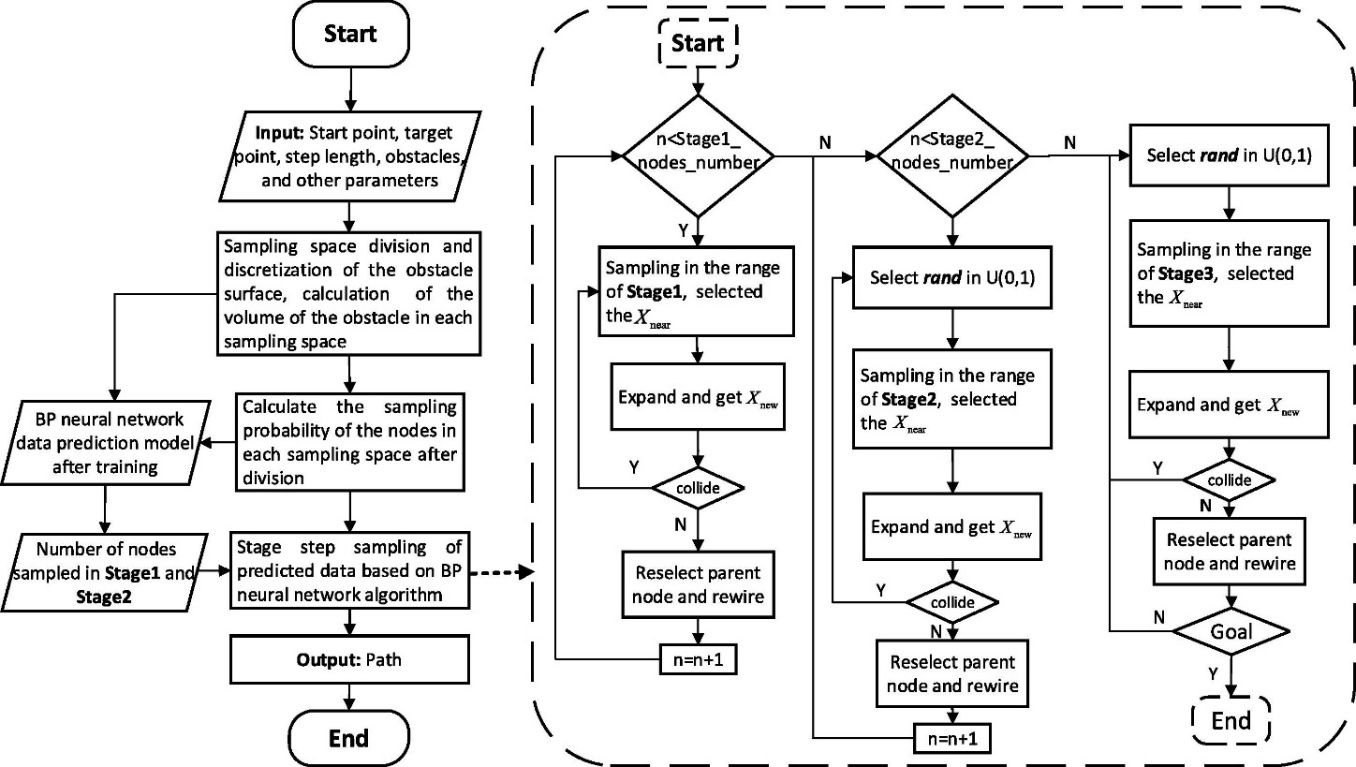
Figure 4: Structure of the RRT-BPNN algorithm [33]

3.1.4. Other hybrid algorithms

This category has less content, with only 2 papers. The algorithms involved are:

• Bidirectional RRT + RRT* [35]

• Q-learning and Neural Network (NN) [36]

In addition to the more typical three types of hybrid algorithms, there are a smaller number of special hybrid algorithms, such as the B-RRT* algorithm, which combines two sampling-based algorithms, and algorithms that combine two machine learning methods.

3.2. Problems solved by hybrid

Hybrid algorithms solve a very large number of problems with obvious effects. The main aspects are as follows: improving the efficiency of path planning, optimising the coordination of the dual manipulator, avoiding local extremes, improving robustness, making the path smoother, solving the multi-objective optimisation problem, and making the motion more stable.

3.2.1. Improving the efficiency of path planning

This is the most prevalent advantage and is achieved by almost all hybrid algorithms. Improvements in path planning efficiency can be seen in terms of reduced search time and shorter path lengths, and since the vast majority of hybrid algorithms possess this property, several algorithms that do not stand out in other respects are selected for analysis here.

In 2014, Pajaziti A. and Cana H. proposed a hybrid algorithm combining neural networks (NNs) and genetic algorithms (GA) to address the shortcomings of NNs with GA. The experimental surface shows that the GA-optimised controller can complete the path in a shorter time, indicating that this algorithm effectively improves the efficiency of path planning [32].

Later, in 2017, Abdi Ali and Adhikari Dibash et al. proposed another hybrid algorithm combining Q-learning and neural network (NN). This algorithm divides path planning into two phases; Q-learning runs the learning code in the first phase, called the active phase, and angle finding by training neural networks in the second phase, called the passive phase. This approach effectively avoids repetitive inverse kinematics computations and reduces the complexity of path planning, thereby reducing runtime [36].

Subsequently, in 2023, Cizmeci Inayet Hakki and Altun Adem Alpaslan proposed the ESSA algorithm, combining the electro-search algorithm (ESO) and simulated annealing (SA), which compared to ESO, this algorithm improves path planning's Compared with ESO, this algorithm improves the solution accuracy and convergence speed of path planning [24]. In the same year, Gao Qingyang and Yuan Qingni et al. proposed the BP-RRT* algorithm, which is based on the backpropagation (BP) neural network and the improved rapid expansion random tree* (RRT*) algorithm. This algorithm optimises the searching ability of BP neural networks to avoid blind searching and therefore improves efficiency [33].

In 2024, Wang Wei proposed a hybrid algorithm combining RRT, RRT-connect and greedy algorithm called SDPS-RRT Connect algorithm, which effectively improves the efficiency of path planning compared to the traditional RRT algorithm [31].

3.2.2. Optimising the coordination of the dual redundant manipulators

In 2023, Dai Jun and Zhang Yi et al. proposed a bi-directional RRT* algorithm that combines RRT with RRT*, which uses a master-slave planning approach. Two manipulators are considered as master and slave manipulators. The path of the master manipulator is planned by B-RRT*, and then the path of the slave manipulator is calculated based on the kinematic closed-chain constraints, which improves the efficiency of the path planning of the dual redundant manipulator arm [35].

3.2.3. Avoiding local extremes

In 2012, Yagnamurthy S. Sai Saran and Chandra M. Sudheer et al. proposed the GA-PSO algorithm to increase population diversity based on the mutation property of genetic algorithms (GA), thus avoiding local maxima in PSO [20].

Next, in 2021, Yuan Qingni and Yi Junhui et al. proposed APF-RRT, a hybrid algorithm based on an improved artificial potential field and a rapidly exploring random tree. This proposes a heuristic for detaching local minima based on the number of neighbouring obstacles, which quickly removes local minima and detaches obstacles [28].

Subsequently, in 2023, Zhuang Min and Li Ge et al. proposed a hybrid algorithm combining the artificial potential field (APF), the A* algorithm and the APF, called the APF-A algorithm. If it is affected by local extremes, then stop using the APF method and switch to the A* algorithm to escape local extremes [25].

3.2.4. Improving robustness

In 2017, Sadiq Ahmed T. and Raheem Firas A. proposed an improved PSO algorithm based on the D* algorithm, and the experimental results showed that this algorithm can effectively find the optimal path even in complex environments with good robustness [21].

Subsequently, in 2024, Liangwu Yu and Jianggui Han et al. proposed a hybrid algorithm combining APF and RRT, where AFP would enhance the target directionality of RRT, making this algorithm more robust and with shorter paths compared to the pure RRT algorithm [29].

3.2.5. Making the path smoother

In 2022, Singh Gurjeet and Banga Vijay Kumar proposed many kinds of novel combinations of heuristic algorithms such as hybrid algorithms like BRO-MRFO, DSO-ChOA and TSA-MOA. These combined algorithms allow the robotic arm to obtain the smoothest trajectory in the shortest time [37]. In the same year, Cao Menglong and Zhou Xinjie et al. proposed a hybrid algorithm based on Radial Basis Function (RBF) neural network and Rapidly Exploring Random Tree (RRT) algorithm, which uses probabilistic sampling strategy to make the tree structure grow faster towards the target point, thus speeding up the planning of RRT algorithm, and introduces the greedy algorithm and the artificial potential field method, which achieves the smoother path. smooth paths [34].

Subsequently, in 2024, Tang Xianxing and Zhou Haibo et al. proposed a hybrid algorithm based on the improved A* algorithm and the artificial potential field method. The enhanced A* algorithm redefines the node search direction and proposes a local path optimisation technique, which results in a smoother trajectory for the robotic arm [26].

3.2.6. Solving the multi-objective optimisation problem

In 2022, Chen Gang and Xu Xinyao et al. proposed the Simulated Annealing Particle Swarm Algorithm (SA-PSA), which consists of a combination of the Simulated Annealing Algorithm and the Particle Swarm Algorithm for solving multi-objective optimisation problems [22].

3.2.7. Making the motion more stable

In 2022, Zhao Jing and Zhu Xijing et al. proposed a new algorithm, IWOA-PSO, which is based on improved whale optimisation and particle swarm optimisation, and improves the efficiency of the manipulator and significantly reduces the jitter of the robotic arm [23].

Subsequently, in 2024, Pu Quan-cheng and Xu Xiang-rong et al. proposed the SA-DOA algorithm. This algorithm, based on QNURBS and an improved dingo optimisation algorithm, takes into account the smoothness of motion, which is ignored by most algorithms, and uses QNURBS to plan the smoothing angle of each joint, resulting in a significant increase in stability [27].

4. Discussion

This paper reviews three main types of robotic arm path planning algorithms. Using keywords like 'robotic arm' and 'path planning,' many studies were found. However, when focusing specifically on algorithms, the number of studies drops significantly. Research on hybrid algorithms is even more limited, mostly appearing between 2022 and 2024. This suggests that hybrid algorithms are still relatively new, likely due to their complexity. Despite this, hybrid algorithms have great potential. As machines take on more complex tasks, a single algorithm may not be sufficient, making the development of hybrid algorithms a necessary trend.

There are still many research gaps in the field of hybrid algorithms.

Firstly, most of the current research has focused on improving the efficiency of path planning, e.g., shrinking computation time, shortening the total path, etc., and there has been virtually no research on multiple robotic arms moving together or in dynamic environments. Compared to continuing to optimise efficiency, research into movement in more complex environments is clearly more in line with future needs.

Second, current hybrid algorithms continue to be dominated by traditional algorithms, with very little integration with machine learning. While the fields of deep learning and reinforcement learning have made great strides since 2022, hybrid algorithms have yet to capitalise on the strengths of these two fields.

Thirdly, very little of the current research has seen actual production, with most of the research being simulations using software, and even if there are products they are mostly confined to the lab, there is a dearth of hybrid algorithms that can be applied to real-world production.

5. Conclusion

In conclusion, this article reviews the dominant conventional algorithms used for robotic arm path planning and the hybrid algorithms that have been used from 2010 to the present day and answers the two questions posed in the introduction. Overall hybrid algorithms are still relatively under-researched, but their advantages and potential are considerable.