1. Introduction

In modern power systems, load forecasting is of crucial importance for the stable operation of the power grid. As pointed out in Ref.[1], accurate power load forecasting can effectively guide the rational arrangement of power generation plans, thereby achieving precise balance between power supply and demand and ensuring the stable and reliable operation of the power grid. If the load forecasting method is ineffective, it may lead to insufficient or excessive power supply, not only causing energy waste but also posing a serious threat to the stability of the power grid. Accurate load forecasting can provide a solid guarantee for the safe and stable operation of the power grid, and is of great significance for the efficient management of power systems and the optimal allocation of resources.

A wide variety of power load forecasting techniques have been adopted in existing research. Ref.[2] focuses on the time-series analysis method, achieving load forecasting through the trend analysis of historical load data. In Ref.[3], researchers use the regression analysis method to establish a mathematical model of the load and related influencing factors for forecasting. In Ref.[4], the grey prediction model is applied to the forecasting of load data with small samples and poor information. Ref. [5] focuses on the BP neural network method, achieving load forecasting through learning from a large amount of data.

However, these traditional methods have certain limitations. Time-series analysis has high requirements for data stationarity. Regression analysis is easily affected by multicollinearity. The grey prediction model has poor adaptability to data with large fluctuations, and neural networks are prone to fall into local optimal solutions. In contrast, artificial intelligence (AI) methods have powerful non-linear mapping and self-learning capabilities, which can better handle complex load data and improve the forecasting accuracy.

This paper proposes a load forecasting method based on the Quantum- behaved Particle Swarm Optimization (QPSO) algorithm and the Long Short-Term Memory (LSTM) network. Firstly, the QPSO algorithm is used to optimize the parameters of the LSTM network. Secondly, the optimized LSTM model is trained to learn the characteristics of load data. Finally, the effectiveness and superiority of this method in load forecasting are verified through case analysis.

2. Load Forecasting Method Based on QPSO-LSTM

2.1. Data Preprocessing

In the task of power system load forecasting, accurate load forecasting is of great significance for ensuring the stable operation of the power system, optimizing the power generation plan, and improving the utilization efficiency of power resources. The original load data we obtain often contains problems such as noise, missing values, and outliers. These problems can seriously affect the accuracy and stability of the prediction model. Therefore, data preprocessing becomes a crucial step.

In the data cleaning process, it is necessary to identify and remove noise data and outliers. Statistical methods such as the 3σcriterion are adopted. Data that deviates from the mean by more than three times the standard deviation is regarded as an outlier and is corrected or removed. For missing values, an appropriate filling method is selected according to the characteristics of the data. The linear interpolation method is used to fill the missing values by linearly fitting the data at adjacent time points. For data with correlations, the regression model is also utilized to fill the missing values based on related variables.

After completing data cleaning, data normalization processing is carried out to unify data with different dimensions into the interval of [0,1] or [-1,1]. Common normalization methods include Min-Max normalization and Z-score normalization. The formula for Min-Max normalization is: \( {x_{norm}}=\frac{x-{x_{min}}}{{x_{max}}-{x_{min}}} \) , \( x \) is the original data, and \( {x_{min}} \) and \( {x_{max}} \) are the minimum and maximum values of the data respectively. The formula for Z-score normalization is \( {z_{i}}=\frac{{x_{i}}-μ}{σ} \) , where \( μ \) is the data mean and \( σ \) is the standard deviation.

2.2. Load Forecasting Method Based on QPSO - LSTM

Traditional load forecasting methods have limitations, however,the development of AI technology provides a new way to solve this problem. As one of the neural network models in AI, the special structural design of LSTM enables it to effectively capture the long-term dependencies in time-series data, making it suitable for time-series problems such as load forecasting. However, the LSTM model has numerous parameters, and the initial parameter setting has a great impact on the model performance. If the parameters are not set reasonably, it is easy to fall into a local optimum, resulting in limited forecasting accuracy. The load forecasting method based on QPSO - LSTM combines the advantages of the Quantum-behaved Particle Swarm Optimization (QPSO) algorithm and the Long Short-Term Memory (LSTM) network, enabling more accurate forecasting tasks.

The LSTM network is a special type of recurrent neural network that can effectively solve the problem of gradient disappearance in the original RNNs. Its core structure includes an input gate, a forget gate, an output gate, and a memory cell.

In the load forecasting method based on QPSO - LSTM, the LSTM network serves as the core time-series processing model, and the operation of its core structure is precisely controlled by a series of formulas. The calculation formulas for the input gate, forget gate, output gate, and memory cell of LSTM are as follows:

Input gate calculation formula: \( {i_{t}}=σ({W_{xi}}{x_{t}}+{b_{ii}}+{W_{hi}}{h_{t-1}}+{b_{hi}}) \)

Forget gate calculation formula: \( {f_{t}}=σ({W_{xf}}{x_{t}}+{b_{if}}+{W_{hf}}{h_{t-1}}+{b_{hf}}) \)

Output gate calculation formula: \( {o_{t}}=σ({W_{xo}}{x_{t}}+{b_{io}}+{W_{ho}}{h_{t-1}}+{b_{ho}}) \)

Memory cell update formula: \( {c_{t}}={f_{t}}⊙{c_{t-1}}+{i_{t}}⊙tanh({W_{xc}}{x_{t}}+{b_{ic}}+{W_{hc}}{h_{t-1}}+{b_{hc}}) \)

Current-time output calculation formula: \( {h_{t}}={o_{t}}⊙tanh({c_{t}}) \)

\( {x_{t}} \) is the input at the current time, \( {h_{t-1}} \) is the hidden state at the previous time, \( {c_{t-1}} \) is the memory cell state at the previous time, \( W \) and \( b \) represent the weight matrix and bias vector respectively, \( σ \) is the Sigmoid activation function,and \( ⊙ \) represents element-wise multiplication.Through the collaborative work of these gates, as shown in the formulas, LSTM can effectively handle the long - term dependence problems in time-series data. In load forecasting, historical load data and influencing factors \( {x_{t}} \) are taken as inputs, and after being processed layer by layer through the LSTM network according to the above formulas, the predicted load value is obtained.

However, the performance of LSTM depends to a large extent on the initialization of parameters such as the weight matrix and bias vector. In order to find the optimal parameters, this paper introduces the QPSO algorithm. The QPSO algorithm is based on the principles of quantum mechanics, and the position and velocity of particles are described by wave functions. In QPSO, the particle position update formula is: \( x_{i,d}^{k}=p_{i,d}^{k}±β\cdot |M_{d}^{k}-x_{i,d}^{k}|\cdot ln(\frac{1}{u}) \) , \( x_{i,d}^{k} \) is the position of the i-th particle in the d-th dimension at the k-th iteration, \( p_{i,d}^{k} \) is the personal best position of the i-th particle in the d-th dimension, \( M_{d}^{k} \) is the global best position, \( β \) is the contraction - expansion coefficient, and \( u \) are random numbers between [0,1]. This formula based on quantum behavior endows particles with stronger global search ability. Compared with the traditional particle swarm optimization algorithm, it is easier to jump out of the local optimal solution.

The steps of the load forecasting based on QPSO - LSTM are as follows: First, collect, clean the historical load power data, and normalize it. Then, initialize parameters such as the positions and velocities of the particle swarm, and the maximum number of iterations. Calculate the fitness value of the particles, find the initial global optimal particle, update the particle positions according to the quantum - behavior formula, recalculate the fitness value and update the global optimum. If the maximum number of iterations has not been reached, continue the iteration; otherwise, stop. Assign the parameters of the optimal particle to the LSTM model. After that, use the pre - processed training data to train the optimized LSTM model, adjust the parameters through the back - propagation algorithm, and learn the patterns of the load data. After training, input the test data to obtain the prediction results. Finally, use the RMSE and MAPE indicators to evaluate and verify the effectiveness and superiority of the prediction method.

3. Case Study

This research focuses on the load forecasting method of LSTM based on QPSO. The load power data of the previous 10 hours are used as input to predict the load power of the next two hours. The entire dataset contains 1,131 load variables. To ensure the training effect and generalization ability of the model, it is divided into a training set and a test set according to a ratio of 70% and 30%. The training set is used to comprehensively train the model and finely adjust its parameters, enabling the model to fully learn the internal patterns and laws in the data. The test set is used to evaluate the prediction performance of the trained model, so as to examine the model's performance in practical application scenarios.

The network parameters of the LSTM load forecasting model based on QPSO are set as follows: the learning rate is 0.005, which coordinates the convergence speed and accuracy of the model. The LSTM layer is set to 2 layers, which can more effectively capture the long-term and short-term dependencies in the time series. The number of hidden layer neurons is 40. Through multiple experiments, it has been verified that this number achieves a good balance between computational efficiency and model performance.

In terms of the selection of case indicators, this paper focuses on the Root Mean Square Error (RMSE) and the Mean Absolute Percentage Error (MAPE). RMSE reflects the average error degree between the predicted value and the true value. The smaller the value, the more accurate the prediction. MAPE shows the prediction error in the form of a percentage, which can more intuitively reflect the relative accuracy of the prediction.

Through the illustration of the typical daily curve, it can be clearly seen that the prediction curve of the LSTM method based on QPSO is highly consistent with the actual load curve, and can well reflect the changing trend of the actual load. To further verify the superiority of this method, it is compared with the LSTM and PSO-LSTM methods. It can be directly observed from the comparison charts of the predicted values and the actual values of each algorithm that the prediction effect of the LSTM method based on QPSO is significantly better than the other two methods, which fully demonstrates the advancement and effectiveness of this method in the field of load forecasting.

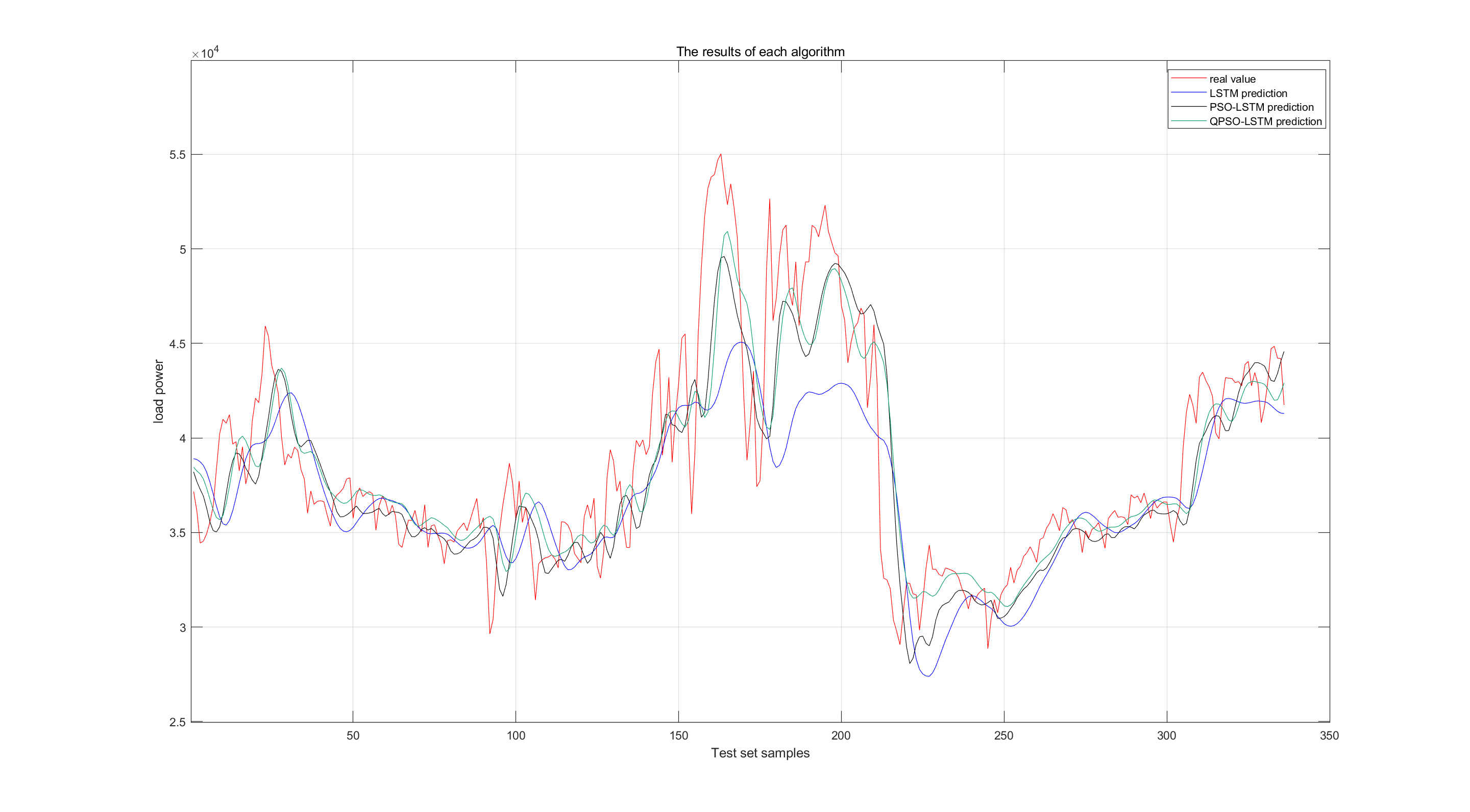
Figure 1: The comparison between the algorithm result prediction and the actual value

The performance indicators of the LSTM, PSO-LSTM, and QPSO-LSTM methods are compared in the figure below. As can be seen from the comparison results of the indicators (shown in the table below), the LSTM method based on QPSO performs outstandingly in terms of the RMSE and MAPE indicators. The average error between its predicted values and the true values is smaller, enabling it to approximate the actual load power data more accurately. This strongly demonstrates its non-negligible advantages in capturing the variation patterns of load data and improving prediction accuracy.

Table 1: Comparison results of each algorithm index

4. Conclusion

This paper proposes a load forecasting method based on QPSO-LSTM. Firstly, the load data is preprocessed. The normalization method is used to map the data to an appropriate interval, and the data is divided into a training set and a test set according to the ratio of the first 70% and the last 30%, preparing for the subsequent model training and testing. Then, an LSTM model is constructed to capture the time-series characteristics of the load data. Subsequently, the QPSO algorithm is introduced to optimize the hyper-parameters of the LSTM model, so as to improve the model performance. Finally, the prediction effect of the model is evaluated through actual test cases. The analysis and comparison of the cases verify that this method has higher prediction accuracy and stability compared with traditional prediction methods, achieving accurate and reliable load forecasting. This method gives full play to the advantages of LSTM in processing sequence data and the global optimization ability of the QPSO algorithm, and can effectively deal with the complexity and uncertainty of load data. In the actual load forecasting work of power systems, this method has important application value and popularization significance.