1. Introduction

At present, most of the tank tops use spherical lattice shell structures that were initially applied to building structures. With the development of tanks towards larger scales, both the storage capacity and diameter of tanks have increased accordingly. Large-span tank top lattice shell structures have become the focus and difficulty of construction [1]. For example, the Lattice Shell structure accumulates a large number of members at its apex, making the structure overly complex. As the number of rings increases in the Kiewitt single-layer lattice shell structure, the number of members on the outer ring will increase significantly, resulting in a sharp increase in steel consumption, decreased economy, and more difficult construction. The Kiewitt-Lamella Shell composite single-layer spherical lattice shell structure formed by combining these two types can effectively solve the above problems [2,3]. The importance of studying the stability of such lattice shell structures on tanks goes without saying.

In order to improve the structural stability to accommodate the ultra-large spans of architectural structures, some scholars have combined prestressed cables with single-layer spherical reticulated shells to create a new type of prestressed reticulated shell structure [4-6]. W. KANG et al. [7] compared and analyzed the reinforced cable-supported dome structure formed by adding cables to the outermost ring with the general cable-supported dome structure, and concluded the advantages and disadvantages of the reinforced structure.

Since prestressed cables can enhance the stability of single-layer spherical shell structures in traditional architecture, it remains to be verified whether combining prestressed cables with the tank shell roof of a storage tank can improve the stability of the tank roof. Therefore, this paper will establish a new type of storage tank prestressed shell roof with prestressed cables and perform static and stability performance analyses on the storage tank shell roof without prestressed cables. This is to verify whether adding prestressed cables can improve the stability of the tank shell roof and to analyze how different sizes and positions of prestress will affect the structure.

2. Research principles and computational models

2.1. Mechanism of action of prestressed cables

After the prestress is applied to the structure, a radial resultant force Pr is formed at the joints towards the inside of the reticulated shell. This force exerts a compressive effect on the dome, causing the shell to contract inwards. Subsequently, an anti-arch action appears in the middle part of the reticulated shell. At the same time, the anti-bending moment generated by the radial force Pr unloads the internal force members of the reticulated shell structure, as shown in Figure 1. Therefore, it can be seen that the peripheral circumferential segmented cable layout can reduce the deflection and outward thrust of the structure, decrease the overall steel consumption of the structure, lower the peak internal force of the members, thereby improving the overall stiffness of the structure and enhancing its economy.

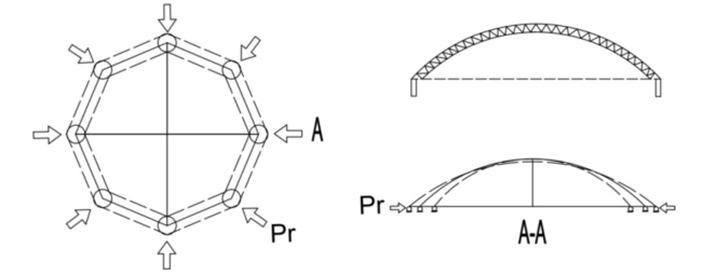
Figure 1: Schematic diagram of space truss deformation

2.2. Stability analysis method

The stability of the space truss structure can be expressed through the analysis of its load-displacement full-process curve. The iterative equation for the load-displacement full-process analysis of the space truss structure is [8]:

(1)

(2)

where K is the tangential stiffness matrix, ΔU is the displacement increment vector, R is the externally applied nodal load vector, F is the nodal force used for element stress, λ is the scalar load factor, and the actual load borne by the structure is λ times the applied load.

Regarding the solution of the above equation, among the existing numerical methods, various improved arc-length control methods are considered to be the most effective methods for tracking the entire process of buckling paths. Different scholars have conducted in-depth studies on the elastic stability and elasto-plastic stability of reticulated shell structures using geometric nonlinear elastic analysis as well as geometric and material double nonlinear analysis. These research efforts have continued to the present day [9,10].

2.3. Analysis model

An overall model of a spherical lattice shell storage tank with Kiewitt-Lianfang grid form is established using ANSYS, with a span of 80m and a rise-to-span ratio of 1/5. The lattice shell members are made of H-shaped steel (Q235), and the prestressed cables are Φ40 high-strength steel rods (pre-tension of 1200MPa). All lattice shell nodes are set as rigid joints, the edge nodes are hinged with the lower support, and the lower boundary of the tank body is considered as a fixed hinge support taking into account the stiffness influence of the tank body. The loads include dead load (1.2kN/m²) and live load (0.5kN/m²). Three cable layout methods are compared: circumferential continuous cable layout, spaced cable layout, and radial cable layout. As shown in figure 2.

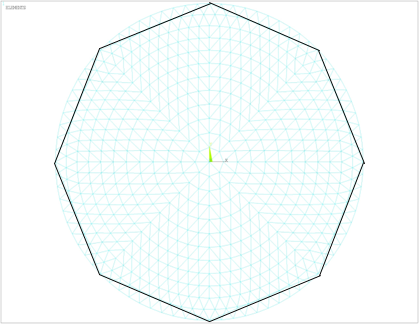
(a) (b)

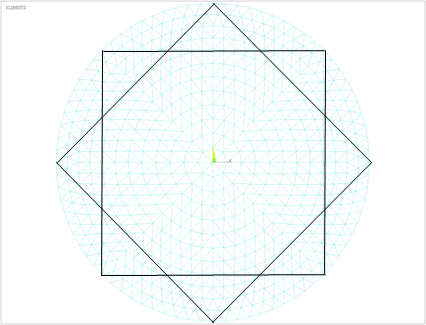
(c) (d)

Figure 2: Overall storage tank and lattice shell models with different cable bracing methods: (a)overall storage tank, (b) Circumferential tendons, (c) Spaced tendons, (d) Radial tendons

3. Research results

3.1. The influence of prestressed cable layout method

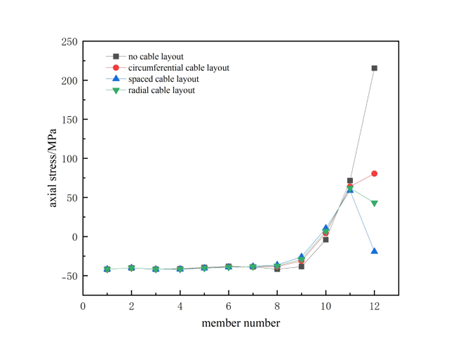
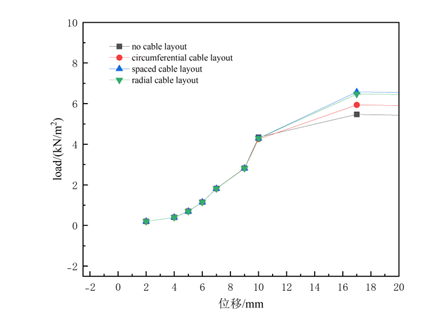
As can be seen from Figure 3, under the same working conditions, the vertical displacement of the lattice shell tank top varies from the inner ring to the outside, increasing first and then decreasing regardless of the cable layout method. Among them, without the use of prestressed cables, the overall lattice shell tank top descends nearly 50mm. However, after the application of prestressed cables, the overall displacement of the lattice shell tank top is improved: when using circumferential cable layout, the overall descent is about 25mm; when using radial cable layout, the overall descent is about 20mm; when using spaced cable layout, the overall descent is about 10mm, and even at the central node, the descent approaches 0mm.Within the inner ring of the lattice shell, the axial stress of the lattice shell members changes little; however, as it approaches the outer ring, for the lattice shell tank top with prestressed cables applied, the axial stress of the circumferential members is greatly reduced. When cables are spaced apart, the circumferential stress even manifests as compressive stress, which is the opposite of the lattice shell tank top without prestressed cables. Among the radial members near the outer ring, the application of prestressed cables also transforms the tensile stress of the lattice shell tank top into compressive stress.The stable ultimate load-bearing capacity of the tank shell roof without cable is 5.468 kN/m². When circumferential cable layout are used, the stable ultimate load-bearing capacity is 5.936 kN/m²; when spaced cable layout are used, the stable ultimate load-bearing capacity is 7.511 kN/m²; when radial cable layout are used, the stable ultimate load-bearing capacity is 7.264 kN/m². Compared with the tank roof without cable layout, the improvement rates of the stable load-bearing capacities of each structure are 8.56%, 37.36% and 32.85% respectively.

(a) (b)

(c) (d)

Figure 3: Comparison of structural performance under different binding methods: (a) Vertical displacement, (b) Internal force of circumferential members, (c) Internal force of radial members, (d) Ultimate bearing capacity

3.2. The influence of prestress magnitude

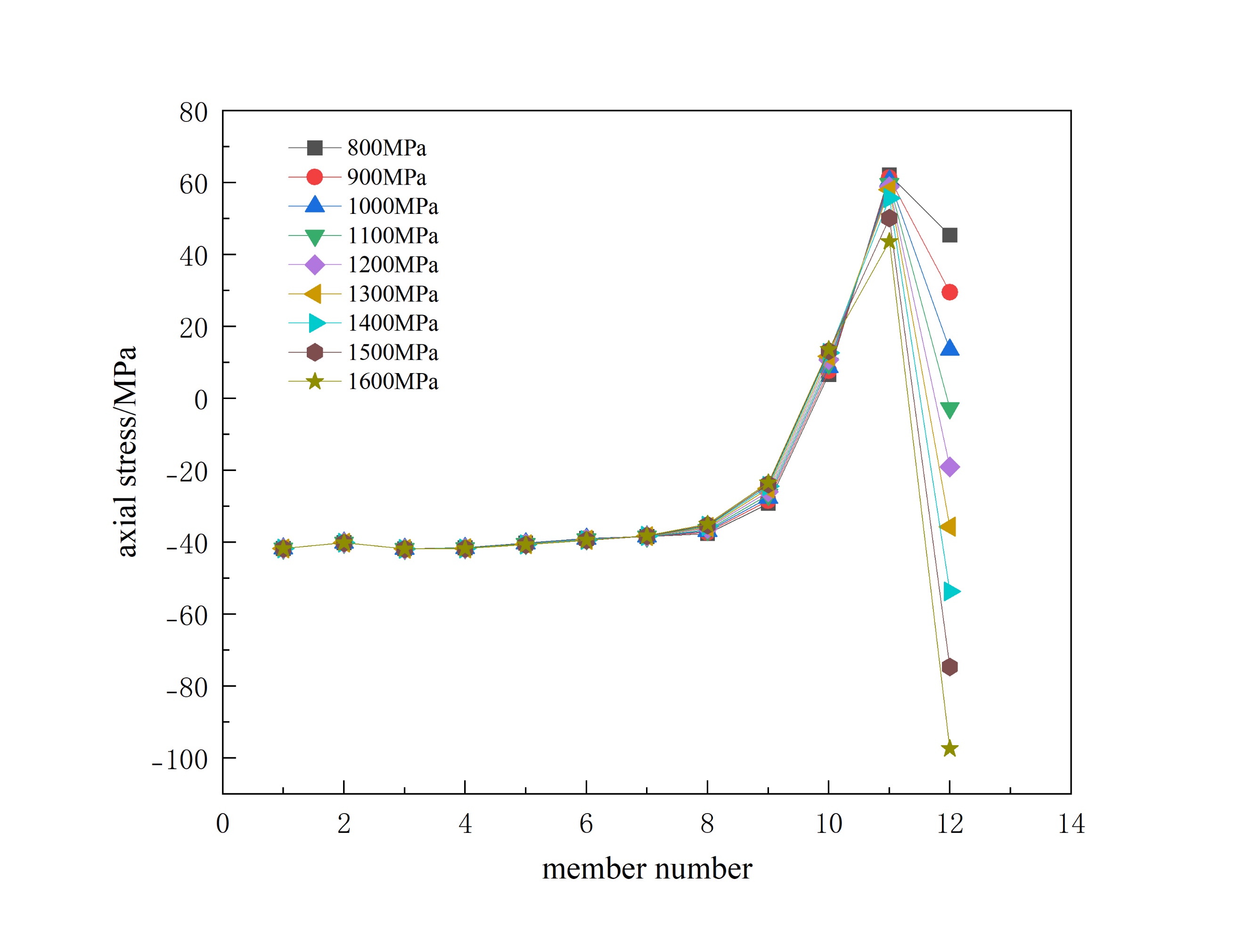
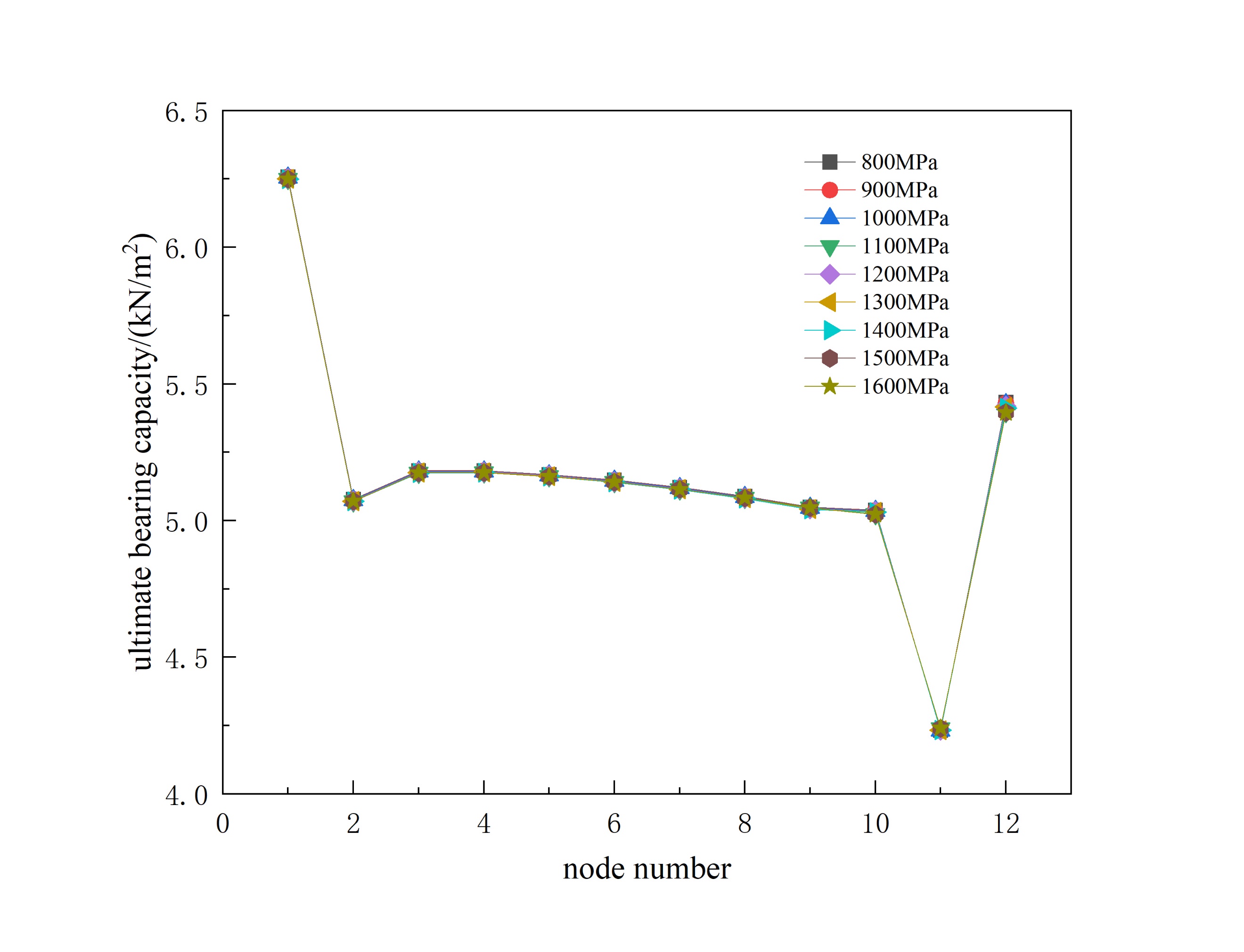
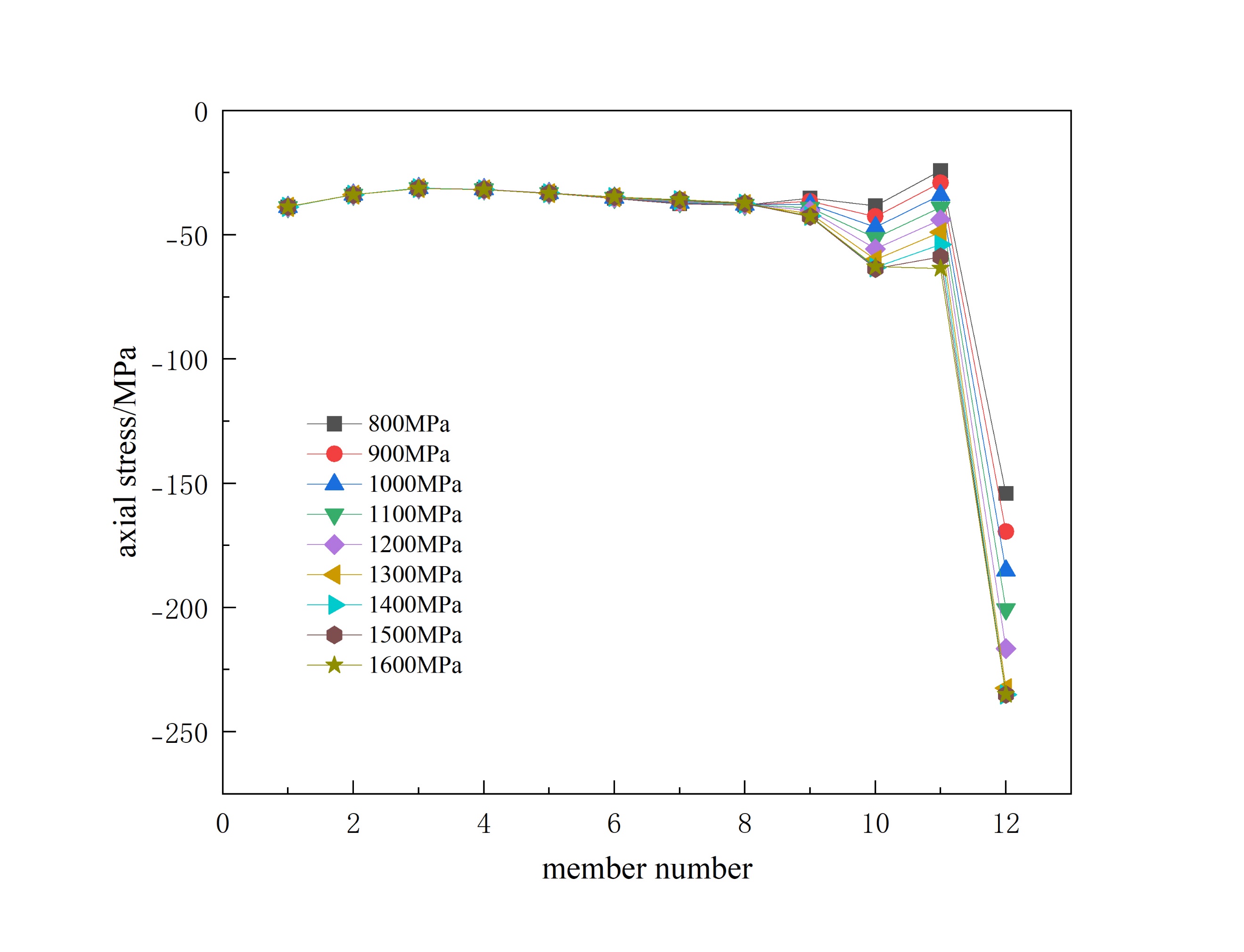
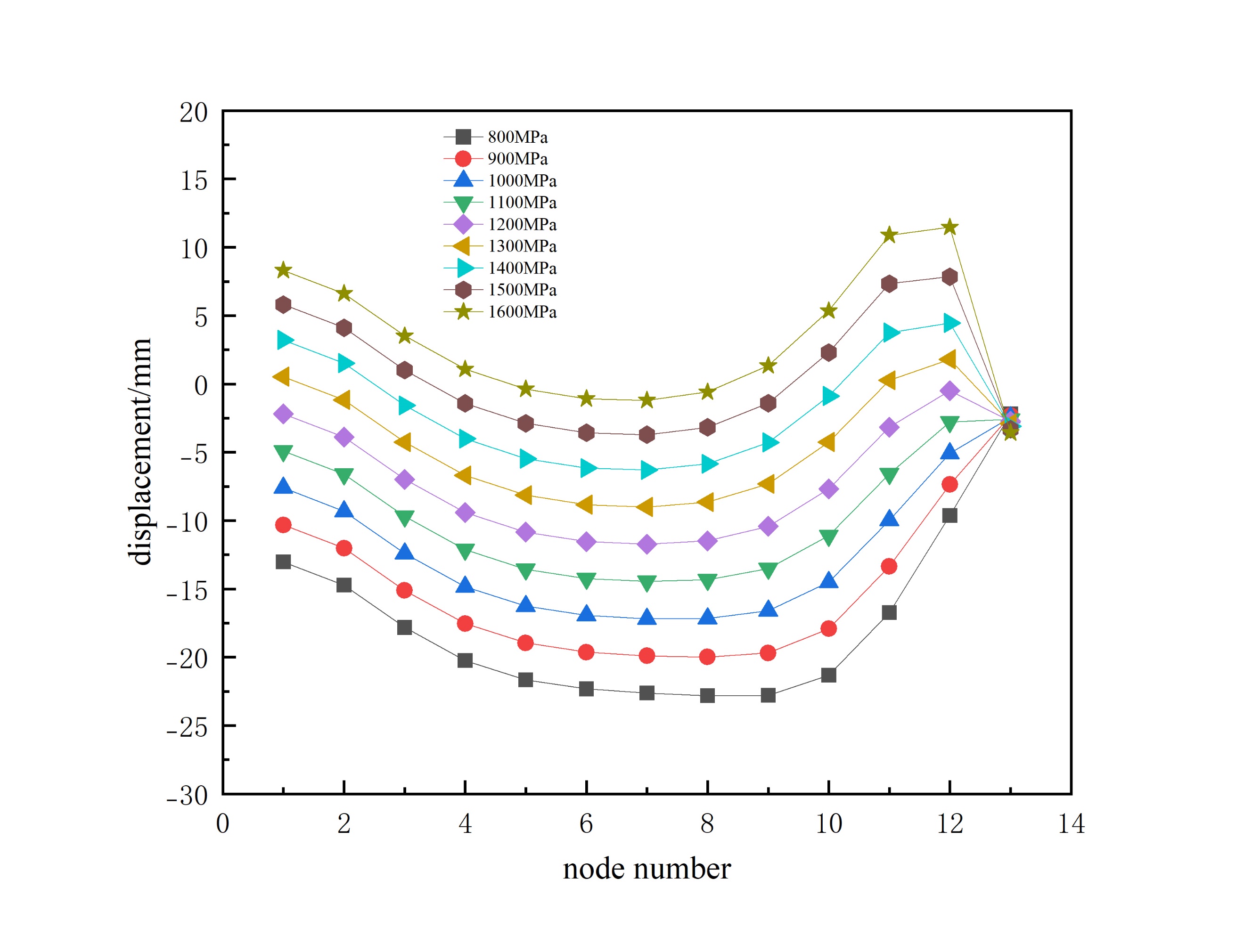Taking the interval cable bracing method as an example, only the magnitude of prestress is changed. Figure 4. show the displacement, internal forces of members, and ultimate bearing capacity of the tank roof structure of the storage tank lattice shell under different magnitudes of prestress.

(a) (b)

(c) (d)

Figure 4: Ultimate bearing capacity of each node of the model under different prestress magnitudes

As the prestress increases, the downward displacement of each node in the model also decreases accordingly, and some nodes even show an upward displacement. Therefore, from the perspective of node displacement, it is best that the applied value of prestress should not be less than 1300 MPa as much as possible. The influence of different prestress magnitudes on the axial stress of members is not significant. As the prestress increases, the axial stress of the circumferential members shows a slight decrease from the 8th ring to the 11th ring, but at the outermost ring, it changes from a gradually decreasing tensile stress to a gradually increasing tensile stress; the axial stress of the radial members shows an increasing phenomenon from the 9th ring to the outermost ring. And as the prestress increases, the ultimate bearing capacity of each node correspondingly decreases, but the degree of decrease is small. Therefore, the magnitude of prestress is not an important condition affecting the stable bearing capacity of the structure.

4. Conclusion

This article establishes a new type of storage tank lattice shell roof model by combining the prestressed cable structure with the storage tank lattice shell roof. The study investigates the stable load-bearing capacity of the roof structure from aspects such as cable layout, magnitude of prestress applied, and its position. The following conclusions are drawn from this study.

(1) Under the same working conditions, the overall displacement of the reticulated shell tank top structure with prestressed cables is significantly improved compared to the overall downward displacement, member internal force distribution, and ultimate bearing capacity of the reticulated shell tank top structure without prestressed cables. These improvements help to increase the overall buckling capacity. In summary, the improvement with spaced cable layout is more significant.

(2) As the prestress increases, the downward displacement of each node in the model also decreases, and the internal force of the members increases, but the force distribution of the structure remains unchanged. The ultimate bearing capacity of each node correspondingly decreases, but the degree of decrease is small. Therefore, the magnitude of prestress applied is not an important factor affecting the stable bearing capacity of the structure.