1. Introduction

With the continuous trend toward larger storage tanks, their construction costs and economic value have also increased significantly, leading to higher safety requirements. Therefore, studying the seismic performance of tank roofs has become particularly important [1,2].

Currently, scholars worldwide have conducted extensive research on the seismic response, seismic performance, and evaluation criteria of lattice shells. Feng et al [3,4] concluded that single-layer lattice shells are in a complex spatial stress state and require multi-dimensional seismic calculations.

Prestressed structures are widely used in large facilities such as gymnasiums [5,6]. Prestressing is a technique that effectively alters the overall stiffness and internal force distribution of a structure by rationally arranging and adjusting the tension in the cables, thereby improving the ultimate load-bearing capacity and controlling structural deformation, which significantly enhances the structural performance.

This new type of prestressed structure lacks analysis of its seismic performance, and its research holds significant reference value for the future development of prestressed lattice shells. Based on the stability analysis of prestressed lattice shells, this paper delves into the seismic performance of prestressed lattice shells for storage tanks. Time history analysis is used to investigate the mechanical behavior of the lattice shell structure under frequent earthquakes, comparing it with traditional structures to evaluate the effectiveness of prestressed cables in enhancing the seismic capacity of the lattice shell.

2. Analysis Model and Methodology

2.1. Analysis Model

The research model selected for this study is a Kiewitt reticulated shell with a span of 60 meters and a rise-to-span ratio of 1/6, divided into 8 fan-shaped sections, as shown in Figure 1. The rings are labeled from the first to the twelfth from the inside out. Since the members are directly in contact with the top skin and need to withstand bending moments, it is appropriate to use I-beams to replace steel circular tubes [7]. The lattice shell is constructed using H350×180×6×8 I-beams made of Q235 steel, with material properties listed in Table 1. The cables have a diameter of Φ30, and the applied cable tension is 800 MPa. The connection between the lattice shell and the tank roof is hinged. The seismic wave selected for analysis is the EI-Centro wave, which is representative of a Class II site. The prestressed lattice shell applies prestress using a peripheral cable arrangement.

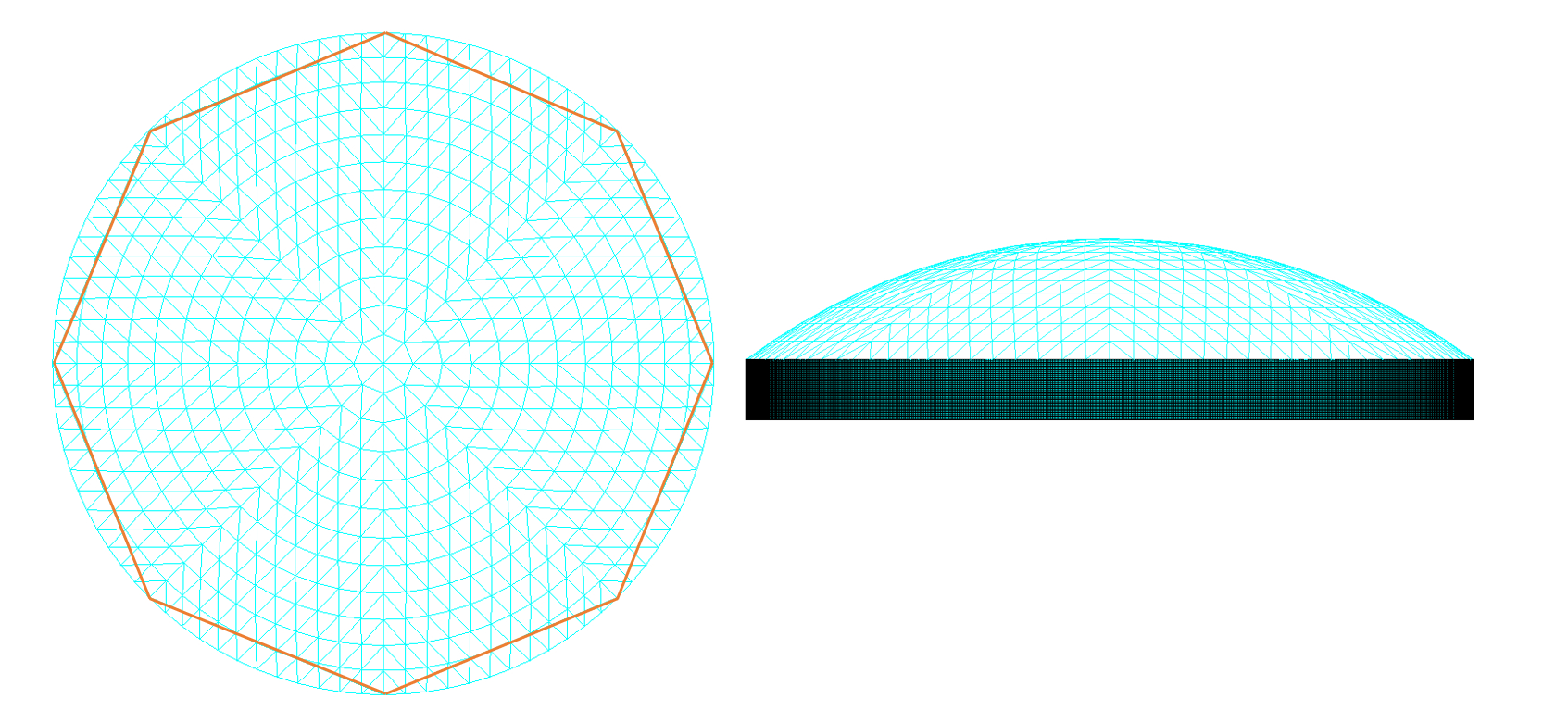
Figure 1: Overall model of the prestressed lattice shell

To make the seismic analysis more efficient, representative nodes and members of the lattice shell are selected for analysis. Due to the symmetrical characteristics of the Kiewitt reticulated shell, the fan-shaped section aligned with the direction of the horizontal seismic wave is chosen as the primary analysis object.

Table 1: Material Properties of the Members

2.2. Characterization Method for Plastic Development in Members

To account for the plastic deformation of the structure under strong seismic actions, the properties of the Beam188 unit integration points are utilized to output plastic strains. The extent to which a member section enters the plastic state can be characterized by whether the plastic strain at each integration point exceeds zero [8]. To facilitate the expression of the degree of member yielding, the following concepts are defined: 1P indicates that 1 to 7 integration points out of the 32 in the member section have entered the plastic state; 8P indicates that 8 to 15 integration points have entered the plastic state; 16P indicates that 16 to 31 integration points have entered the plastic state; and 32P indicates that all 32 integration points in the section have entered the plastic state, as illustrated in Figure 2.

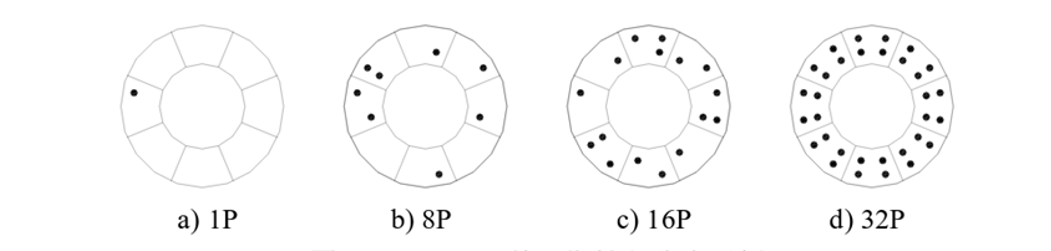
Figure 2: Example of Plastic Integration Points in Beam188 Element.

3. Frequent Seismic Analysis

To conduct a comprehensive seismic analysis of the lattice shell structure under frequent earthquakes and to thoroughly investigate the impact of prestressed lattice shells on seismic performance, prestressed lattice shells with prestress magnitudes ranging from 600 MPa to 1200 MPa are selected for comparative analysis. These are compared with the seismic responses of conventional Kiewitt lattice shells to explore the seismic performance of the new prestressed lattice shell structure.

3.1. Displacement Response Characteristics

By analyzing the horizontal and vertical displacements, the seismic resistance of the prestressed cables in both horizontal and vertical directions is evaluated. The distribution pattern of member displacements across the rings is examined. The seismic wave used is the Taft wave, with a seismic intensity of 8 degrees, representing a frequent earthquake scenario. The seismic wave is applied in three directions with intensities in the ratio of 1:0.85:0.65, and the effect of gravity is considered.

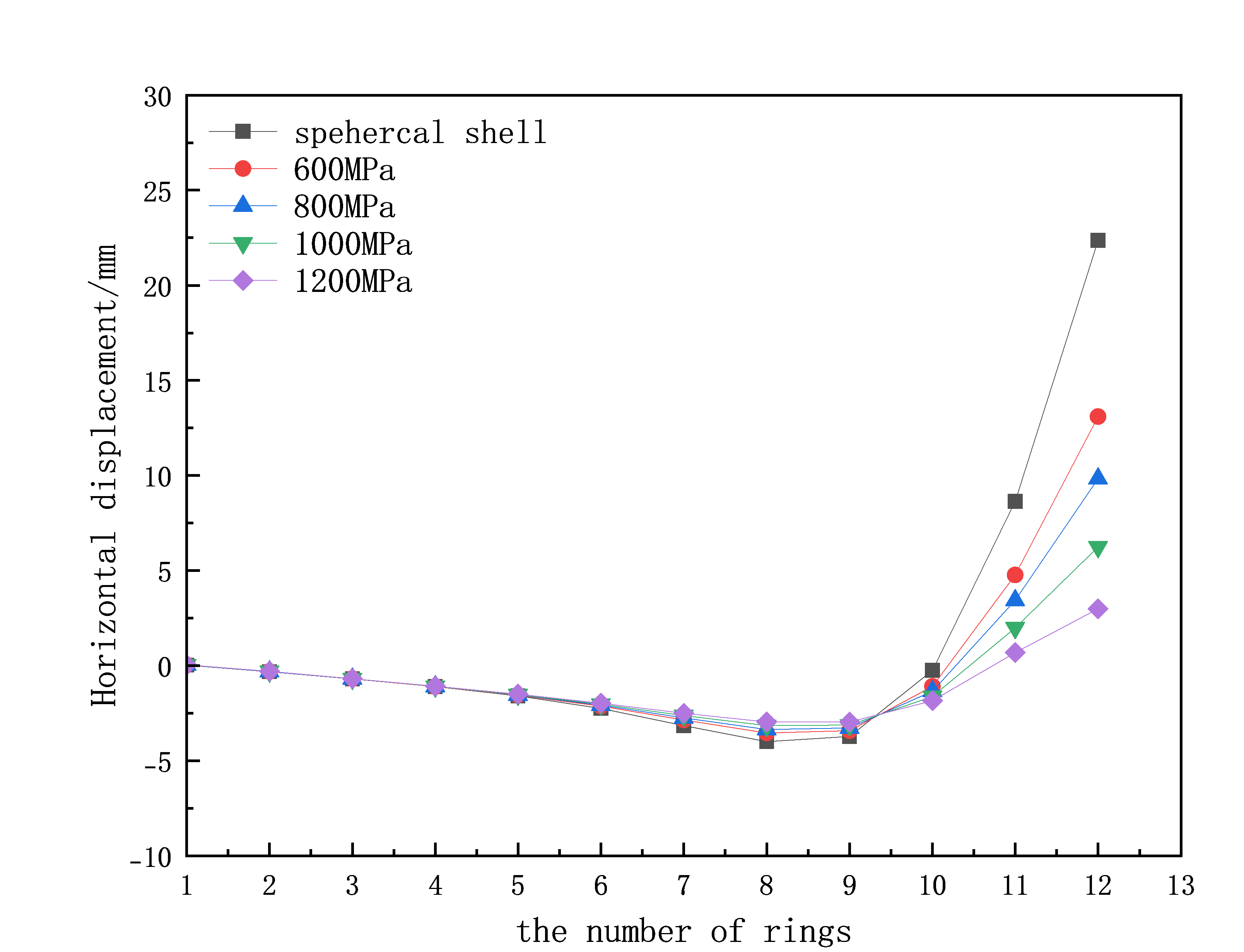
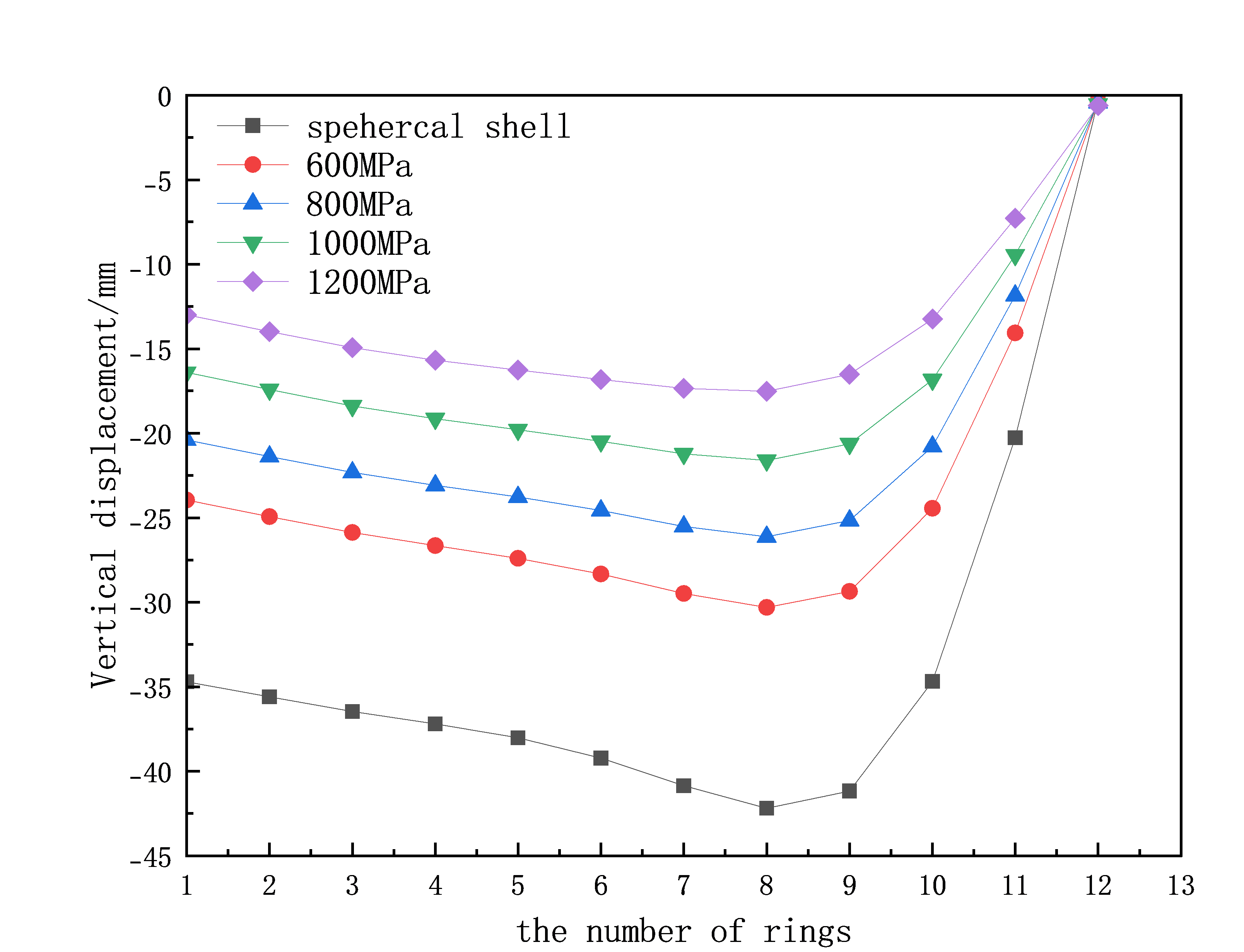
(a) (b)

Figure 3: (a) Horizontal displacement of axial members under different cable forces; (b) Vertical displacement of axial members under different cable forces.

Seismic analysis under frequent earthquakes is conducted separately for the single-layer spherical lattice shell and the prestressed lattice shell to explore the impact of prestressed cables on the seismic performance of the lattice shell. From Figure 3(a), it can be observed that the horizontal displacement patterns of the axial members in the first few rings of both the spherical lattice shell and the prestressed lattice shell are generally consistent. The horizontal displacements of the 11th and 12th ring members are significantly affected, and as the prestress increases, the horizontal displacement of the axial members gradually decreases. From Figure 3(b), for the prestressed lattice shell, as the prestress increases, the vertical displacement of the axial members gradually decreases, demonstrating that the prestressed cables effectively reduce the vertical displacement of the structure.

3.2. Stress Response of Members

The members of the single-layer spherical lattice shell primarily bear axial forces, with relatively small bending stresses. Therefore, the study of its seismic performance focuses on analyzing the distribution of axial seismic internal forces in the members. To thoroughly investigate the improvement in internal forces brought by the prestressed lattice shell to the single-layer lattice shell, the prestress magnitude of the cables is varied, using the same parameters as in Section 3.1. The stress conditions of different members under seismic action are examined.

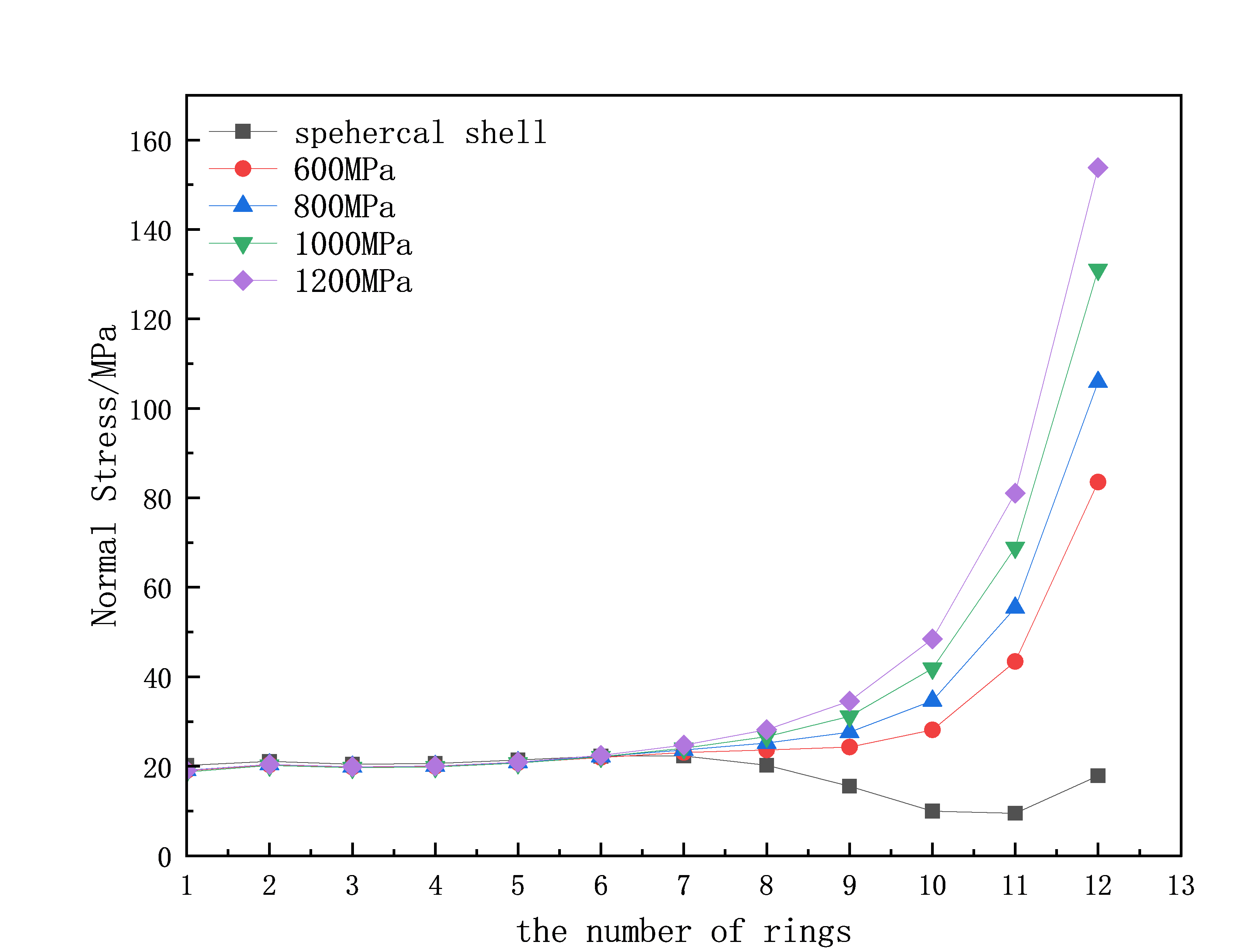
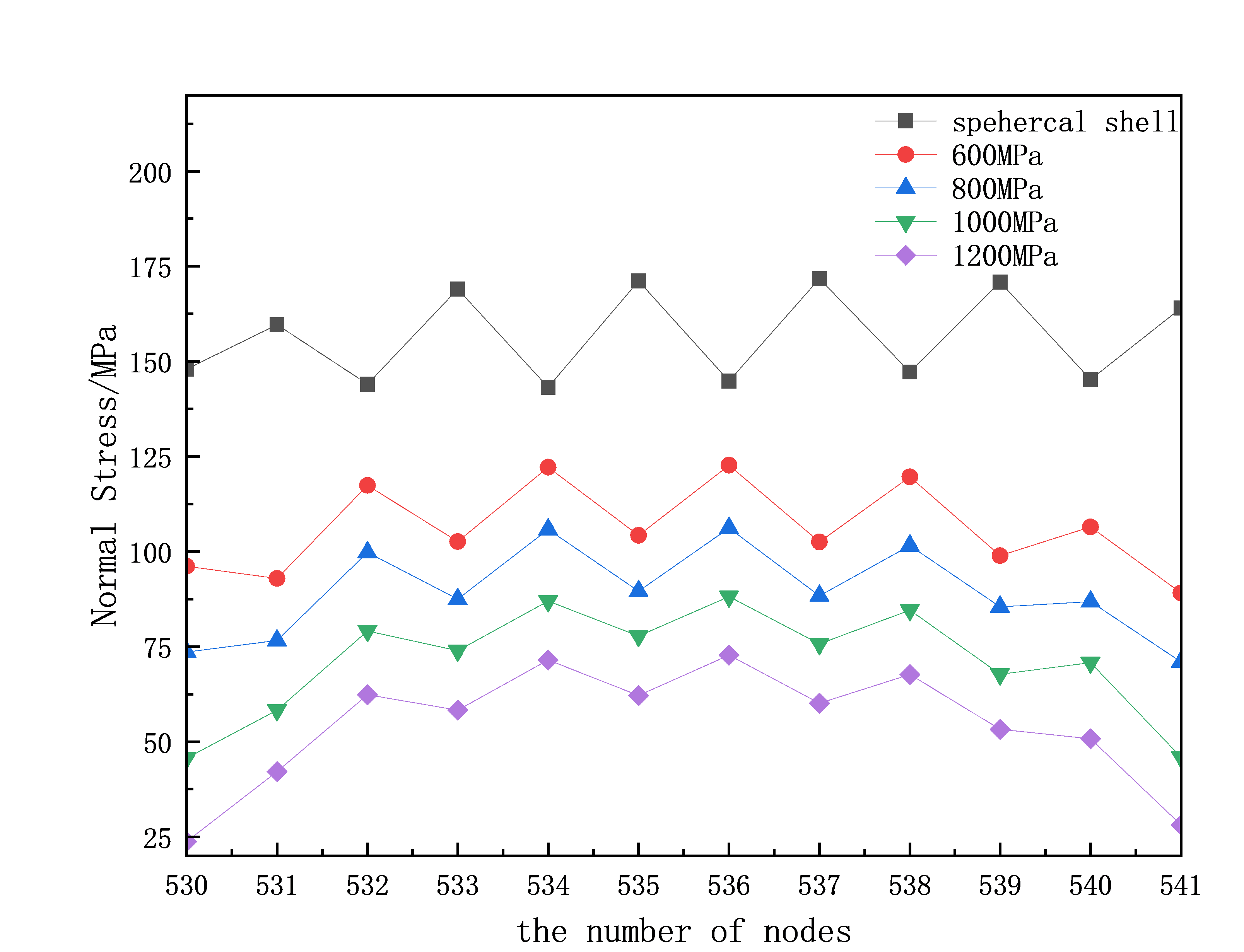
(a) (b)

Figure 4: (a) Axial stress diagram of axial members at different rings; (b) Axial stress diagram of ring members in the 12th ring fan-shaped section

From Figure 4(a), it can be observed that the axial stress of the axial members is larger in the first 8 rings, decreases in the middle rings, and then increases again in the outer rings. For the prestressed lattice shell, the axial force of the axial members begins to increase at the 8th ring, and as the prestress increases, the axial force of the axial members also increases. The axial stresses of the 12th and 11th ring axial members significantly exceed those of the single-layer lattice shell. From Figure 4(b), it can be seen that the axial force of the ring members within a fan-shaped section varies within a range, much higher than that of the axial members, indicating that the outer ring members are more susceptible to damage. At the same time, as the prestress of the prestressed lattice shell increases, the average axial force of the ring members gradually decreases, demonstrating that the prestressed cables significantly improve the axial stress distribution of the ring members, with greater prestress leading to better results.

3.3. Influence of Different Cable Forces on Seismic Performance

Through displacement and stress response analysis, it can be observed that increasing the tension in the prestressed cables effectively reduces the seismic response of the lattice shell. Therefore, it is necessary to explore the influence of prestress magnitude on seismic performance. From Table 2, which compares the maximum displacement and peak internal forces of the lattice shell under different prestress levels, it can be seen that as the prestress increases, the reduction rate of structural deflection increases, indicating that higher prestress levels better improve the structure's response to vertical seismic actions. However, the reduction rate of the peak internal forces in the members first increases and then decreases. This is because the prestressed cables reduce the horizontal thrust on the members, thereby improving the stress conditions of the outermost ring members, but they also increase the peak internal forces in the axial members.

Table 2: Maximum Displacement and Peak Internal Forces of Members Under Different Prestress Levels.

By comparing the effects of different axial forces, it can be concluded that as the prestress in the cables increases, the effectiveness of the prestressed cables in improving the vertical seismic performance of the lattice shell also increases. However, higher prestress is not always better. Excessive prestress can lead to the connected members bearing overly large axial forces, thereby reducing the overall seismic performance. Therefore, the magnitude of the prestress should be selected based on the peak internal forces of the members.

4. Conclusions

This paper primarily investigates the seismic response of the prestressed lattice shell structure under frequent earthquakes and the damage sequence under strong seismic actions. The specific conclusions are as follows:

(1) Time history analysis is used to study the displacement and stress response of the prestressed lattice shell under frequent earthquakes. The results indicate that the prestressed cables significantly reduce the seismic response of the lattice shell in the vertical direction, compensating for the lack of stiffness in the vertical direction. Furthermore, they improve the stress distribution in the outer rings of the lattice shell, reducing the displacement and stress in these regions.

(2) Through the analysis of the displacements of the prestressed reticulated shell under frequent earthquakes, it is evident that the prestressed cables can effectively reduce both the vertical and horizontal displacements of the shell. The primary area of influence is the outer ring of the shell's members, thereby diminishing the structure's seismic response.

(3) The prestressed cables can reduce the horizontal displacement of the outer members, but the members connected to the cables experience significant tensile stress, leading to inward displacement. Therefore, when designing the prestressed cables, the appropriate prestress magnitude should be selected based on the peak internal forces of the members, and the cross-sectional area of the members at the cable connection points should be reinforced.