1. Introduction

Beyond its mathematical achievements, the Fibonacci sequence is also frequently observed in nature, as evidenced in the arrangement of bees, nautilus and sunflower [1]. This natural phenomenon has inspired extensive research into its properties and applications. One of the key motivations for this study is to explore the implementation of the Fibonacci sequence in Python programming, particularly in generating the sequence efficiently and analyzing its role in the Euclidean Algorithm, which is a classical method for computing the greatest common divisor (GCD) of two integers. The Fibonacci sequence exhibits unique mathematical properties that influence various computational algorithms, including the Euclidean Algorithm [2]. The Fibonacci sequence has been widely applied across various fields due to its low computational complexity and cost-effective nature. In computer science, it is commonly used in searching, hashing, and random number generation [3]. In financial markets, Fibonacci retracement is employed as a technical analysis tool for predicting price movements [4]. Additionally, Fibonacci numbers play a significant role in biological and chemical systems, influencing protein models and genetic patterns [5]. Despite its wide application, research gaps remain in optimizing the efficiency of Fibonacci calculations in programming and exploring deeper mathematical relationships in computational algorithms. Many studies have focused on Fibonacci's use in theoretical mathematics, but fewer have analyzed its integration into programming paradigms like Python, C, C++ and Java particularly in GCD computations using the Euclidean Algorithm. This study aims to bridge this gap by examining how an engineer can implement in Python for generating these sequences and optimizing the GCD function.

2. Methods to Construct the Fibonacci Sequence

The Fibonacci sequence is a fundamental concept in mathematics and computer science. It consists of a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. Mathematically, it is expressed as: \( F(n) = F(n-1) + F(n-2) \) where F(0)=0 and F(1)=1. In Python, there are multiple ways to generate Fibonacci numbers, each with its advantages and disadvantages, which depend on what you value the most. This study will demonstrate how different codes can create a Fibonacci sequence with different space and time complexity.

2.1. Recursive Method (Less Efficient)

A straightforward yet inefficient method that most students can think of for generating Fibonacci numbers is recursion

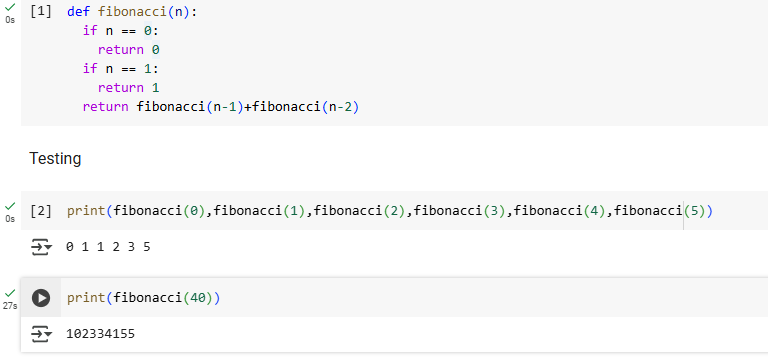
Figure 1: The process of creating the Fibonacci sequence and calculating specific numbers using a recursive method

The coding in Figure 1 follows a self-referential structure, where each function call depends on the results of two previous calls. This method provides a clear and intuitive implementation but suffers from significant inefficiencies in terms of time complexity. One of the major drawbacks of recursion is exponential growth in function calls. Each recursive call spawns two additional calls, leading to a time complexity of O(2ⁿ). As a result, the computation time increases rapidly as the input size grows. For instance, calculating the 40th Fibonacci number as the picture shows using recursion takes several seconds, while some small Fibonacci numbers may be faster than some big numbers like 40. Moreover, the recursive method exhibits high memory consumption due to stack overflow risks. Since each recursive call is stored in memory until it resolves, deep recursion may exceed system limits, causing the program to crash. This issue makes recursion impractical for large values of n, while the recursive approach is conceptually simple and easy to implement. It is not efficient for handling large inputs, especially in this AI era. Alternative methods, such as dynamic programming or iteration, are preferable for optimizing performance and reducing memory usage.

2.2. Iterative Fibonacci Algorithm: (Most Efficient)

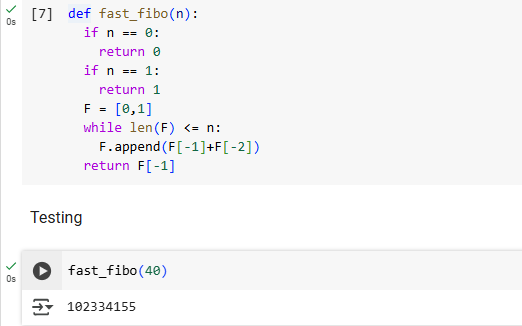
Figure 2: the processes of generating Fibonacci numbers with an iterative approach

Figure 2 shows the faster Fibonacci algorithm to create Fibonacci numbers with an iterative approach. Unlike the recursive method, which involves repeated function calls, this implementation stores previously computed values in a list, ensuring that each Fibonacci number is calculated only once. One of the key advantages of this method is its time complexity of O(n). The while loop iterates from 2 to n, while each iteration requires a constant number of operations. This contrasts sharply with the recursive approach, which has an exponential time complexity of O(2ⁿ) due to repeated function requests. As a result, the iterative approach is much more suitable for computing large Fibonacci numbers. On the other hand, the space complexity of this method is O(n) because it maintains a list to store all Fibonacci numbers up to n, which can turn time costs into space complexity. While this is more efficient than the recursive approach, which requires O(n) space for function call stacks, it is still suboptimal for memory usage. However, the iterative approach provides greater computational efficiency and mitigates stack overflow issues, offering a superior alternative to the recursive method. For most practical applications, it is the preferred method due to its balanced trade-off between performance and the simplicity of implementation.

3. The other Function of Fibonacci

3.1. Reasons to consider alternative questions

After discussing the fundamental properties of the Fibonacci sequence, it is natural to explore its connections to other fields of mathematics. One classic example is the greatest common divisor (GCD), a fundamental problem in number theory. The GCD of two integers is the largest number that divides both without leaving a remainder. Computing the GCD effectively and correctly is crucial in various applications, such as cryptography, numerical computing, and algorithm design. One of the most well-known techniques for solving this problem is the Euclidean algorithm, which follows a recursive structure remarkably similar to the Fibonacci sequence. The Euclidean algorithm is one of the most efficient methods compared to other algorithms, while its time complexity is commonly stated as O(log(min(a, b))).

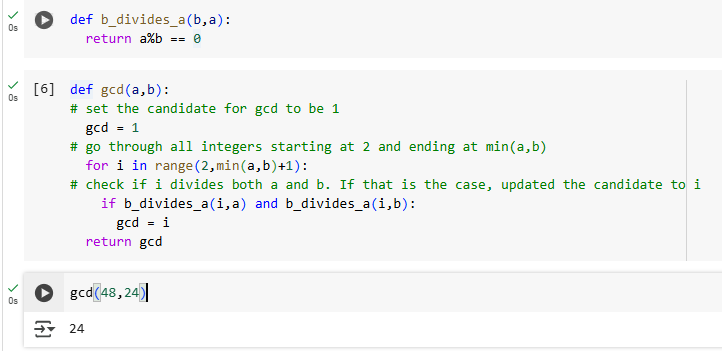
Figure 3: the function of GCD by the Brute-Force method.

3.2. Analyzing the Computational Efficiency of the Brute-Force GCD Algorithm and the Superiority of the Euclidean Method

The given algorithm in Figure 3 is a straightforward approach to calculating the greatest common divisor (GCD) of two integers, which follows a brute-force strategy by iterating through all possible divisors from 2 to min(a, b), so its efficiency is relatively low. Since the loop runs from 2 to min(a, b), the worst-case time complexity is O(min(a, b)). This means that for large values of a and b, the algorithm may take a significant amount of time to complete. Additionally, the approach relies on iterating through all potential divisors, making it less efficient compared to more optimized methods. A more efficient alternative is the Euclidean algorithm, which significantly reduces the problem size at each iteration through the application of the modulus operation. To comprehend the derivation of its complexity, a thorough examination of the algorithm’s iterative process and underlying mathematical properties is required.

Figure 4: More efficient algorithms for optimizing functions.

3.3. The Euclidean Algorithm’s Efficiency: Exploring Complexity through Fibonacci Numbers and the Golden Ratio

The logic of the code in Figure 4 mainly comes from the Euclidean algorithm and its complexity is just O(min(a, b)). To determine the maximum number of steps required, we must consider the worst-case scene. It has been established that the slowest reduction occurs when a and b are consecutive Fibonacci numbers [6]. In such cases, the sequence of modulus operations follows the Fibonacci recurrence relation: Fn​ mod Fn−1​=Fn−2​. This means that each step reduces the problem size according to the Fibonacci sequence. Since Fibonacci numbers grow approximately according to the formula:

\( F(n) ≈ 1/√5 × ϕⁿ \) (1)

where ϕ (the golden ratio) is approximately 1.618, the number of steps required to reach 1 is proportional to \( {log_{∅}}{min⁡(a,b)} \) which simplifies to O(log min(a,b)). This characteristic ensures that the number of steps required is inherently logarithmic, resulting in a time complexity of O(log min(a, b)). Accordingly, the Euclidean method demonstrates a significantly higher level of computational efficiency, especially when dealing with large numerical values.

4. Analysis of Fibonacci's Impacts

Having examined the Python code, we now comprehend the generation of the Fibonacci sequence and its interrelation with the greatest common divisor (GCD). Notably, the complexity of the Euclidean algorithm is constrained by Fibonacci numbers, making it a fundamental concept in computational efficiency, data structures, and cryptography. Additionally, the influence of the Fibonacci sequence extends far beyond mathematical computations. This numerical pattern is applied widely in nature, biology, financial markets, architecture, and even in music and art. Many complex natural phenomena and modern technologies function by Fibonacci-based structures, highlighting their universal presence and significance in the real world.

(1) Fibonacci in Technology and Computing

In computer science, the Fibonacci sequence is widely used in algorithm design and data structures. For instance, enhancing the efficiency of priority queue operations, which are essential for optimizing graph algorithms like Dijkstra’s shortest path algorithm. Additionally, Fibonacci numbers are widely used in recursive algorithms, dynamic programming, and hashing techniques, helping to improve computational efficiency.

(2) Fibonacci in Financial Markets

In finance, the Fibonacci sequence is usually used for technical analysis, particularly in Fibonacci retracement levels. Traders use these levels (23.6%, 38.2%, 61.8%) to predict potential price movements in stocks, forex, and cryptocurrencies, as these percentages often represent natural points of support and resistance in market trends.

(3) Fibonacci in Nature and Biology

Numerous natural patterns adhere to the Fibonacci sequence. The arrangement of leaves on a stem, known as phyllotaxis, the spiral configurations in sunflowers and pinecones, and the proportional dimensions of seashells and hurricanes all manifest Fibonacci ratios. This mathematical structure facilitates optimal sunlight exposure for photosynthesis in plants, thereby illustrating its evolutionary advantage.

(4) Fibonacci in Architecture and Design

Architects and designers will use Fibonacci proportions. From ancient Greek temples to modern skyscrapers, the Golden Ratio (φ ≈ 1.618) plays an important role in aesthetically pleasing structures and visual harmony and balance. It is also found in graphic design, photography, and logo creation, contributing to the beauty of various artistic compositions.

(5) Fibonacci in Music and Art

Musicians and composers, including Bach and Mozart, have structured compositions using Fibonacci numbers, arranging notes, rhythm, and sections based on these ratios. In visual arts, the Golden Spiral, derived from Fibonacci proportions, guides the composition of paintings and photographs, enhancing their appeal.

The Fibonacci sequence is not just a mathematical function but a fundamental principle woven into the fabric of modern life. Whether in technology, finance, nature, architecture, or art, its influence is vast and undeniable. Understanding and applying Fibonacci principles can lead to better efficiency, innovation, and aesthetic appeal in many industry fields. Beyond theoretical computations, Fibonacci numbers also play a crucial role in various real-life applications. They are widely observed in nature (such as leaf arrangements and shell spirals), financial markets (through Fibonacci retracement in stock trading), architecture and design (utilizing the golden ratio for aesthetic harmony), and even music and art (where Fibonacci proportions enhance composition). These applications demonstrate the far-reaching influence of Fibonacci mathematics on both science and everyday life.

5. Conclusion

In this paper, we have investigated the generation of the Fibonacci sequence using Python and evaluated the efficiency of the iterative Fibonacci algorithm in comparison to the recursive method. The iterative method optimizes performance by converting time complexity into space complexity, allowing for significant reductions in execution time. By carefully evaluating computational costs and specific requirements, we can leverage this method to achieve better efficiency. Additionally, we investigated the greatest common divisor (GCD) problem and analysed why the Euclidean algorithm with a time complexity of O(log min(a, b)). This efficiency is closely linked to the Fibonacci sequence, as Lamé, G.’s theorem states that the number of steps in the Euclidean algorithm is bounded by the Fibonacci sequence, reinforcing the deep mathematical connection between these concepts. Beyond theoretical computations, Fibonacci numbers also play a crucial role in various real-life applications. They are widely observed in nature (such as leaf arrangements and shell spirals), financial markets (through Fibonacci retracement in stock trading), architecture and design (utilizing the golden ratio for aesthetic harmony), and even music and art (where Fibonacci proportions enhance composition). These applications demonstrate the far-reaching influence of Fibonacci mathematics on both science and everyday life.

Despite the insights gained in this study, certain limitations remain. Our discussion primarily focused on basic algorithmic efficiency without delving into advanced optimizations such as matrix exponentiation or memoization, which can further enhance Fibonacci sequence computations. Additionally, while we highlighted the connection between Fibonacci numbers and the Euclidean algorithm, deeper exploration into their implications for modern cryptography and data structures remains an open field for future research. As AI demands continue to grow, it is essential to seek even more optimized algorithms that balance efficiency and resource consumption to calculate and handle huge information. We hope that researchers will build upon these foundations in the future, optimizing existing methods and exploring new applications of Fibonacci mathematics in fields ranging from computing to artificial intelligence. By doing so, we can drive further innovation and push the boundaries of algorithmic efficiency.