1. Introduction

Electrocatalysts serve as fundamental elements for energy conversion and storage technologies, as their performance directly influences the efficiency of key processes such as hydrogen generation through water electrolysis, the utilization of fuel cells, and the conversion of CO₂. With the increasing global demand for clean energy, developing electrocatalysts that are both highly efficient and cost-effective has become an urgent research priority in materials science and chemical engineering. Conventional electrocatalysts are predominantly noble metals such as Pt and Pd. To lower costs and improve catalytic performance, researchers have increasingly explored non-noble metal alternatives, including Fe-, Ni-, and Co-based catalysts [1]. However, traditional catalyst design has largely relied on empirical trial-and-error methods, making them both time-consuming and resource-intensive while lacking the predictive capability to elucidate reaction mechanisms at the atomic scale, thereby hindering the rational design of next-generation catalysts.

Density functional theory (DFT) is a fundamental tool in quantum chemistry, widely employed in condensed matter physics, materials science, and catalyst design due to its high computational efficiency and moderate accuracy. In contemporary chemical industries, catalysts serve a crucial function, as their efficiency directly impacts energy conversion, green chemistry, and sustainable development. In recent years, with the rapid advancements in computational chemistry and computing power, DFT-based theoretical studies have become a crucial approach for elucidating the fundamental nature of catalytic reactions and guiding catalyst design. By analyzing reaction pathways, transition states, electronic structures, and surface adsorption characteristics, DFT has been increasingly applied in catalysis, providing robust theoretical support for experimental research. Despite its significant contributions to catalytic studies, DFT still faces several challenges, such as accuracy limitations in handling strongly correlated systems (e.g., transition metal oxides) and constraints in simulating reaction kinetics and long-range interactions [2].

To address these challenges, this study systematically investigates the electronic structure characteristics and reaction mechanisms of catalysts through density functional theory, in conjunction with specific catalytic systems such as the oxygen reduction reaction and carbon dioxide reduction reaction. The theoretical framework mainly discusses the historical development of DFT and widely adopted exchange-correlation functionals, such as the Local Density Approximation (LDA), Generalized Gradient Approximation (GGA) and Perdew-Burke-Ernzerhof (PBE) [3,4]. Based on this foundation, we summarize DFT-based catalyst design strategies. Through DFT calculations, we analyze the electronic density distribution on catalyst surfaces, identify active sites, and explore their interactions with reactant molecules. Furthermore, we examine reaction pathways and transition states, compute reaction energy barriers, and unveil the intrinsic nature of catalytic reactions. Ultimately, this study aims to provide theoretical guidance for catalyst design, offering insights to optimize existing catalysts and develop novel catalytic materials.

2. Fundamentals of density functional theory

2.1. Development history of DFT

The origins of density functional theory (DFT) can be traced back to 1927, when Thomas [5] and Fermi [6] proposed the Thomas-Fermi model, which was the first to apply statistical mechanics to explore electron distribution within atoms and construct the uniform electron gas model. However, this model exhibited significant accuracy limitations due to its failure to account for exchange interactions. A major breakthrough came in 1964 when Hohenberg and Kohn introduced the Hohenberg-Kohn theorem (HK theorem) [7], which rigorously demonstrated a direct relationship between the ground-state electron density and the external potential. Furthermore, it proposed the core principle that the electron density, which minimizes the total energy, represents the exact ground-state density of the system, providing a robust theoretical basis for DFT. The following year, Kohn and Sham successfully derived the renowned Kohn-Sham (KS) equation based on the local density approximation (LDA) [8]. This approach elegantly transformed the complex many-electron density functional problem into a solvable single-electron wave equation, significantly improving the accuracy of kinetic energy contributions in practical calculations and greatly expanding the applicability of DFT. In recent years, the deep integration of DFT with molecular dynamics methods has led to remarkable advancements in materials design, synthesis, computational simulations, and performance evaluations. As a result, DFT has become a core theoretical tool in tool in fields such as condensed matter physics, materials science, and quantum chemistry, offering a robust framework for interdisciplinary research.

2.2. Common exchange-correlation functionals

2.2.1. Local density approximation (LDA)

The core assumption of LDA is that within an infinitesimally small volume element, the electron density is locally uniform. This allows the entire system to be divided into numerous such small volume elements, where the electron behavior within each element approximates that of electrons in a uniform electron gas. Mathematically, it is expressed as equation(1):

\( {E_{xc}}[p](r)=∫{E_{xc}}[p](r)P(r){d^{3}}r \) (1)

where E_xc[ρ] represents the exchange-correlation energy functional, ρ(r) denotes the electron density, ∫d³r is a three-dimensional integral, and ε_xc[ρ](r) corresponds to the exchange-correlation energy density. LDA demonstrates certain advantages in describing systems with uniform or weakly varying electron density distributions. However, its accuracy often falls short when dealing with systems where electron density undergoes significant variations.

2.2.2. Generalized gradient approximation (GGA)

As a major improvement over LDA, GGA explicitly incorporates the influence of the electron density gradient on the exchange-correlation energy functional, overcoming LDA’s limitation of relying solely on the local electron density values at each spatial point. In practical applications, GGA provides a more accurate description of electron behavior in non-uniform electron gas systems, significantly enhancing computational accuracy. Consequently, it exhibits greater adaptability and reliability when addressing a wide range of chemical and physical problems.

2.2.3. Perdew-burke-ernzerhof (PBE) exchange functional

Introduced in 1996 by John Perdew, Kieron Burke, and Matthias Ernzerhof, the PBE functional was developed to improve the accuracy of density functional theory (DFT) by refining the description of electron correlation effects [3]. It is commonly employed in computational chemistry and condensed matter physics software such as Material Studio, VASP, and Gaussian, where it is integrated as a standard method for handling electron exchange-correlation. Users can input basic information, such as the unit cell structure and atomic positions, and the software can efficiently perform DFT calculations using the PBE functional, providing quick access to essential material properties, including electronic structure and energy. This facilitates material research and design by offering reliable theoretical support.

3. Theoretical research on catalysts

3.1. Sabatier principle

The Sabatier principle emphasizes that a catalyst must maintain a delicate balance between the adsorption and desorption of key intermediates throughout the reaction [9]. In essence, a catalyst’s activity depends on the strength of its interactions with reactants. If adsorption is too strong, the reactant or intermediate binds too tightly to the catalyst surface, blocking steps like desorption. Conversely, if adsorption is too weak, the catalyst cannot efficiently capture the reactant, slowing the reaction. Therefore, the most effective catalyst strikes an ideal balance between adsorption and desorption, ensuring efficient and continuous catalytic reactions.

3.2. D-band theory

The d-band theory was proposed by Professor Nørskov in 1995 to analyze the variation in binding strength between transition metal catalysts and adsorbates [10]. This theory established a solid theoretical foundation for subsequent research on scaling relations and volcano plots, making it one of the most influential theoretical frameworks in heterogeneous catalysis. Essentially, it represents a simplified version of the Anderson-Newns model, providing an effective framework to describe adsorbate–surface interactions and highlighting that adsorption of atoms or molecules on transition metal surfaces is a key factor in heterogeneous catalysis.

In d-band theory, the d-band center energy is identified as a crucial descriptor for predicting adsorption energy. The core concept lies in understanding the electronic band structure of d-orbitals on the surface of transition metal catalysts and the diverse effects this unique structure has on catalytic reactions. Due to their distinctive properties, the d-orbital electrons of transition metals actively participate in chemical bonding, thereby playing a significant role in determining catalytic activity, selectivity, and stability.

In practical catalyst design and optimization, d-band theory serves as an indispensable guiding principle. By precisely tuning the crystal structure of catalysts, it is possible to alter atomic arrangements and lattice parameters, thereby modulating the position and width of the d-band center. Adjustments in chemical composition, such as introducing different elements or modifying element ratios, can effectively reshape the electronic structure, leading to modifications in the d-band characteristics. Additionally, optimizing surface properties, such as modifying surface roughness or defect density, allows for fine-tuning of the d-band structure.

Optimizing the d-band structure through these strategies enables the achievement of several key objectives: Enhancing catalytic activity: Precise adjustment of the d-band center's position and width can significantly strengthen the adsorption capability of the catalyst toward reactants. This enhancement leads to higher reaction rates and improved catalytic efficiency, thereby boosting overall catalytic activity; Improving selectivity: By accurately tuning the d-band structure, catalysts can be designed to selectively promote desired reaction pathways. Adjusting the distribution and energy states of d-orbital electrons allows catalysts to favor target reactions while suppressing side reactions, thereby increasing product purity and yield and optimizing reaction selectivity. Enhancing stability: A well-regulated electronic structure can increase catalyst resistance to poisoning, making it less susceptible to impurities or harmful species. Furthermore, optimized d-band characteristics improve thermal stability, ensuring that catalysts maintain robust performance across varying temperature conditions. This, in turn, prolongs catalyst lifespan, reduces operational costs, and minimizes replacement frequency.

4. Application of density functional theory in catalyst design

4.1. Oxygen reduction reaction (ORR)

The oxygen reduction reaction (ORR) is one of the core electrochemical catalytic process, serving as the cathodic reaction in proton exchange membrane fuel cells (PEMFCs). It significantly influences fuel cell energy conversion efficiency and involves several electron transfer steps. Reaction pathways vary depending on the electrolyte environment (acidic or alkaline). In an acidic medium, the primary reaction pathway is O₂ + 4H⁺ + 4e^- → 2H₂O; whereas in an alkaline medium, it follows O₂ +2H₂O + 4e^- → 4OH^-. However, the sluggish reaction kinetics of ORR severely limits fuel cell performance, prompting extensive research into the development of highly efficient ORR catalysts.

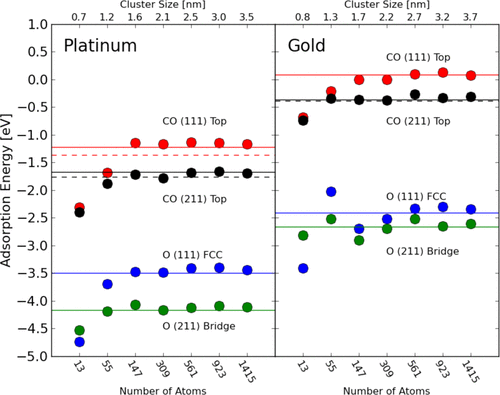
Figure 1: Calculated adsorption energies of O and CO on the (111) plane and stepped facet on platinum and gold clusters [11]

In the early stages of ORR research, Pt-based catalysts became the primary focus due to their relatively high catalytic activity. As shown in Figure 1, Wei et al. investigated the ORR reaction mechanism on Pt surfaces using density functional theory (DFT) calculations [12]. Their study revealed that the d-orbital electronic structure of Pt atoms is closely related to ORR activity. By adjusting the size and shape of Pt nanoparticles, the coordination environment of surface atoms can be altered, thereby influencing catalytic performance. This research provided essential theoretical guidance for optimizing Pt-based catalysts, forming the foundation for subsequent studies aimed at improving Pt utilization and reducing costs.

With the advancement of research, non-precious metal catalysts have gradually gained attention. For instance, Andrew A et al. reported a non-precious metal ORR catalyst based on Fe–N–C materials [12]. By combining experimental studies with DFT calculations (Figure 2), they elucidated the crucial role of Fe–N active sites in the ORR process. Their findings indicated that the coordination structure between Fe atoms and surrounding N atoms facilitates the effective adsorption and activation of oxygen molecules, thereby reducing the reaction energy barrier.

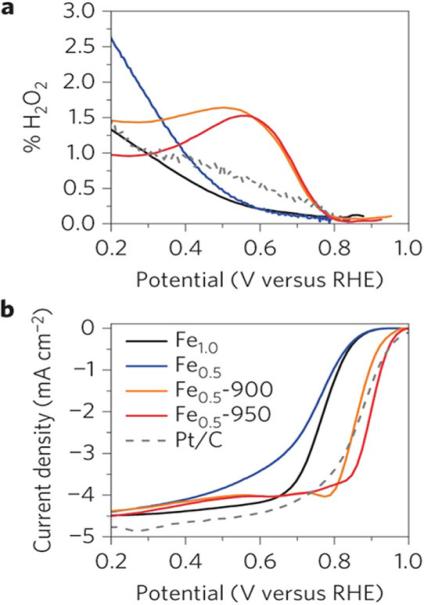
Figure 2: RRDE measurements recorded in O2-saturated electrolyte, pH=1, for a series of prepared NPM catalysts and commercial Pt [13]

This catalyst showed performance alkin to that of Pt-based catalysts under alkaline conditions, opening new avenues for the design of non-precious metal ORR catalysts. In recent years, single-atom catalysts (SACs) have achieved significant breakthroughs in the field of ORR. Peng et al. demonstrated that single Co atoms dispersed on specific supports form a unique electronic structure [14], enabling precise regulation of the ORR reaction pathway (Figure 3). This significantly enhances catalytic activity and selectivity. The emergence of SACs has introduced a novel approach and direction for ORR catalyst design.

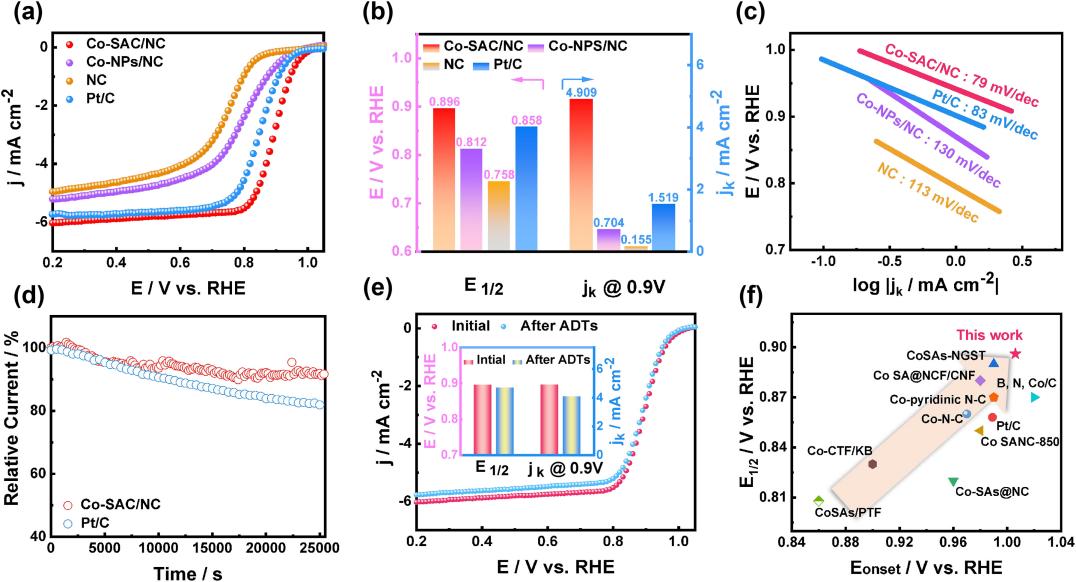
Figure 3: Electrochemical performance of the as-prepared catalysts [14]

4.2. Carbon dioxide reduction

The CO₂ reduction reaction (CO₂RR) holds significant importance in mitigating global greenhouse effects and achieving carbon cycling. It is also one of the most prominent research areas in catalysis. This goal of this reaction is to transform CO₂ into valuable chemicals or fuels, such as carbon monoxide (CO), methanol (CH₃OH), and formic acid (HCOOH). However, due to the high chemical stability of CO₂ molecules, the reduction process faces considerable challenges.

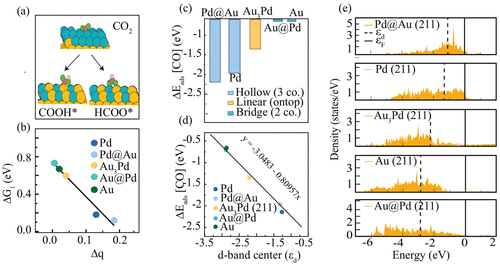
Sakshi et al. synthesized a series of Pd-Au bimetallic alloy catalysts and employed density functional theory (DFT) calculations to investigate their catalytic mechanisms in detail (Figure 4) [15]. The results revealed that electronic interactions within the bimetallic alloy could effectively optimize the catalyst's electronic structure, enhancing CO₂ adsorption and activation. Additionally, these interactions reduced the binding energy of key reaction intermediates, thereby improving both the reaction rate and selectivity. This study provides critical theoretical support and practical guidance for the application of bimetallic alloy catalysts in CO₂ reduction.

Figure 4: DFT calculation of Pd-Au bimetallic alloy catalysts [15]

Subsequently, metal-organic framework (MOF)-based catalysts have emerged as promising materials in CO₂ reduction. Deng et al. reported a novel MOF-derived catalyst[16], demonstrating through integrating experimental studies with DFT calculations, it was demonstrated that the unique porous structure and tunable active sites of MOFs could effectively adsorb and convert CO₂ (Figure 5). This catalyst exhibited high CO₂ reduction activity and selectivity under mild conditions, providing a new material platform for designing efficient CO₂ reduction catalysts.

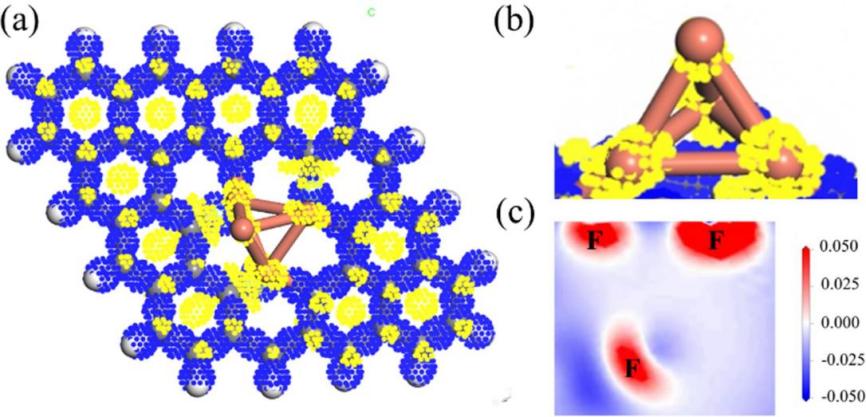
Figure 5: (a) Isosurface map of the differential charge density on the Cu₄-FDG surface and (b) the Cu₄cluster. the blue and yellow regions represent electron density increase and decrease, respectively. (c) two-dimensional slice of the differential charge density for the F atom in Cu₄-FDG, where the blue and red regions indicate electron depletion and accumulation, respectively [16]

Recently, bimetallic alloy catalysts have also shown great potential in CO₂ reduction reactions. In early studies, metal catalysts such as Cu were widely explored for CO₂ reduction. Duan et al. employed DFT calculations to investigate the reaction pathways and active sites on Cu surfaces, revealing that the crystalline structure and surface morphology of Cu significantly influenced CO₂ adsorption and activation [17]. Different crystal facets and defect sites exhibited varying catalytic activities, offering theoretical insights for the design and optimization of Cu-based catalysts. Subsequent research further enhanced the catalytic performance of Cu nanoparticles by controlling their morphology and size.

5. Conclusion and outlook

In conclusion, this study, utilizing density functional theory (DFT), systematically analyzes the electronic structure and reaction mechanisms of catalysts in oxygen reduction and carbon dioxide reduction systems. Through theoretical calculations, the applicability of functionals such as LDA, GGA, and PBE has been reviewed, and their roles in catalyst design have been explored. By studying the electronic density distribution on catalyst surfaces, active sites, and their interactions with reactants, key reaction pathways and energy barrier variations have been clarified. The research reveals the correlation between electronic structure parameters (e.g., d-band center) and catalytic activity, elucidating the kinetic limitations of different reaction steps. These findings provide a theoretical foundation for optimizing catalyst performance, such as reducing noble metal usage and designing single-atom catalysts, with potential applications in energy conversion and carbon reduction.

Despite the significant advances DFT has enabled in catalyst design, challenges remain in predicting complex catalytic systems. One major difficulty lies in accurately simulating dynamic catalytic reactions, which involve multiple intermediates and intricate transformations. Conventional DFT studies, primarily focused on static mechanisms, struggle to describe these dynamic processes. In high-temperature and high-pressure reactions, precise modeling of surface atomic behavior, as well as adsorption-desorption processes, is crucial. Future advancements should integrate kinetic simulations and experimental data to develop dynamic DFT or quantum dynamics approaches, refining models through experimental validation to enhance the simulation of complex reactions.

Additionally, research on catalyst stability and degradation mechanisms remains limited. Experimental methods face challenges in directly observing degradation processes, such as surface structural changes and active site deactivation. While DFT can theoretically predict degradation trends, accurately describing structural reconstruction and deactivation is still difficult. Future studies should focus on these mechanisms by investigating structural and electronic evolution under different conditions, constructing theoretical models of stability, and integrating experimental findings to guide the development of long-lasting catalysts.

Another challenge is the quantification of reaction selectivity, as multiple intertwined factors influence selectivity outcomes. While DFT can clarify reaction pathways and energy barriers, accurately predicting selectivity remains difficult. Future research should integrate statistical mechanics and machine learning techniques to comprehensively consider multi-factor synergistic effects. Developing new computational tools will enhance DFT’s predictive capability for reaction selectivity, driving continuous innovation in catalyst optimization and new material discovery. These advancements will support sustainable development in energy conversion and the chemical industry, contributing to the global transition toward a green and low-carbon future.