1. Introduction
Mobile robots have been widely used in industry, agriculture, military and other industries [1], and path planning is just the key problem that mobile robots need to consider in the movement process. With the development of robot related technologies, such as robot control, automation, sensor, network technology, mobile robots are more and more widely used. Among them, for the transportation of dangerous goods in the chemical industry, mobile robot transportation has become an important way to solve this problem. For the transportation of dangerous goods in unknown complex environment, the path planning problem of mobile robot needs further exploration. According to the degree of the mobile robot's understanding of the environment, path planning methods can be divided into global path planning based on prior complete information [2] and local path planning based on sensors [3]. Global path planning requires the mobile robot to master all the environmental information, such as fences, obstacles, etc., to plan the path according to all the information on the environmental map, and then generate an optimal path. At present, the commonly used algorithms mainly include grid method [4], A * algorithm [5], particle swarm algorithm [6], ant colony algorithm [7], and reinforcement learning method [8]. Q-learning algorithm is a time series differential control algorithm under off orbit strategy in the reinforcement learning method proposed by Watkins in 1989. When the standard Q-learning algorithm is applied to path planning, there are problems such as slow convergence speed and long learning time.
However, global path planning has a large amount of computation and is not suitable for exploring unknown environments, while local path planning only needs to collect the surrounding environment information in real time through mobile robot sensors, understand the map information and local obstacle distribution, and then select the optimal path from the current node to the target node. For complex unknown environments, mobile robots still need to process a large number of sensor data, which consumes time and computing resources, making mobile robots move slowly. However, with the emergence of reinforcement learning, the problem of slow path planning for mobile robots in unknown environments has been alleviated. Reinforcement learning is a branch of machine learning, which is mainly used to solve decision-making problems. RL is essentially a Markov decision process [9] (MDP). The basic idea of RL is that in the continuous interaction with the environment, the agent learns an optimal strategy to maximize the rewards obtained from the environment. RL is independent of the environment, does not need a priori complete environment information, only needs to interact with the current surrounding environment, so RL is very suitable for path planning with unknown environments. Q-learning algorithm is one of the most important path planning algorithms based on reinforcement learning. It does not require the prior information of the environment model. For any limited MDP, Q-learning will find an optimal strategy to maximize the expected value of the total reward in all the next consecutive steps, starting from the current state. The traditional Q-learning algorithm mainly uses ε- Greedy search strategy, which is a strategy of balanced utilization and exploration. In traditional methods, fixed factors are used. For complex unknown environments, there are problems such as slow convergence, long time consuming, and unstable movement. In order to speed up the search for paths and improve the stability of agent movement, this paper proposes a dynamic ε- Greedy search strategy, through the dynamic adjustment of factors, makes the path search speed faster, and reduces the number of turns, and enhances the stability of the robot's movement to transport goods.
2. Standard Q-learning algorithm
Q-learning algorithm is a temporal difference learning method under off orbit strategy. A key assumption about Q-learning is that the interaction between agent and environment is regarded as a Markov decision-making process. In Q-learning, the evaluation value of each status work pair (s, a) is Q (s, a). The evaluation value is defined as the total discount that will be returned if the current related actions are executed and a policy is followed. The optimal evaluation value can be defined as the sum of discount returns obtained by executing action a in the current state s and then executing according to policy π.
3. Results and discussion
3.1. Environment and action space
In order to ensure the complexity and randomness of the experimental environment, four different experimental environments were set up. The environment is represented by rectangles and circles of different sizes, which are limited to a 50 * 60 border. For the movement of the agent, the experiment sets four directions, namely up, down left and right, which are represented by arrays [0,1,2,3]. The moving distance of the agent is set to 1 each time, so that the agent can have full opportunities to explore the environment in the experimental environment..
3.2. Dynamic ε- Greedy search strategy
• Specify an exploration rate "epsilon" and set it to 1 at the beginning. This is the step size we will use randomly. At the beginning, this rate should be at the maximum, because we do not know any value in Q-table. This means that we need to do a lot of exploration by randomly selecting actions.
• Generate a random number. If this number is greater than epsilon, then we will "use" (which means that we use the information we already know to select actions at each step). Otherwise, we will continue to explore.
• At the beginning of training Q function, we must have a large epsilon. As the agent becomes more confident about the estimated Q value, we will gradually reduce epsilon.
• To better set epsilon, reduce epsilon according to the number of iterations.
4. Experiment and analysis
The effectiveness and advancement of the algorithm are verified by simulation experiments. Because of the universality and practicality of grid modeling [10], the experimental environment in this paper uses grid modeling.
4.1. Experiment 1
|
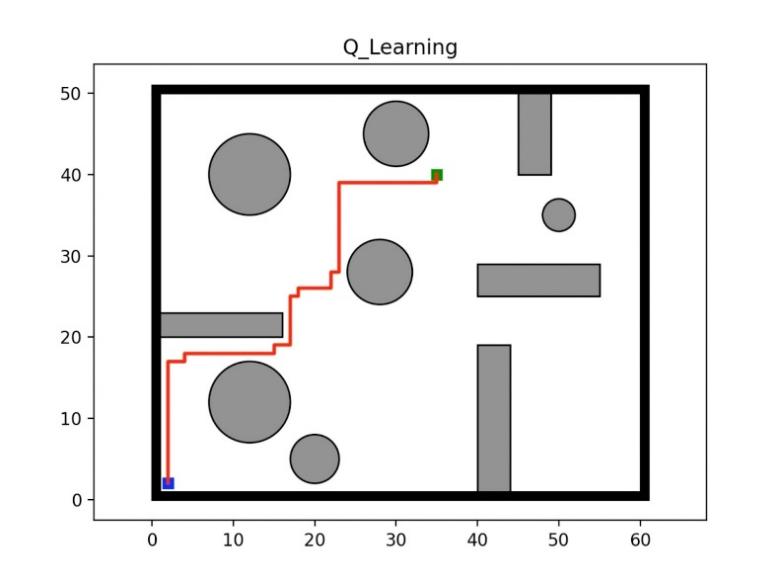
Figure 1. Path planning diagram1. |
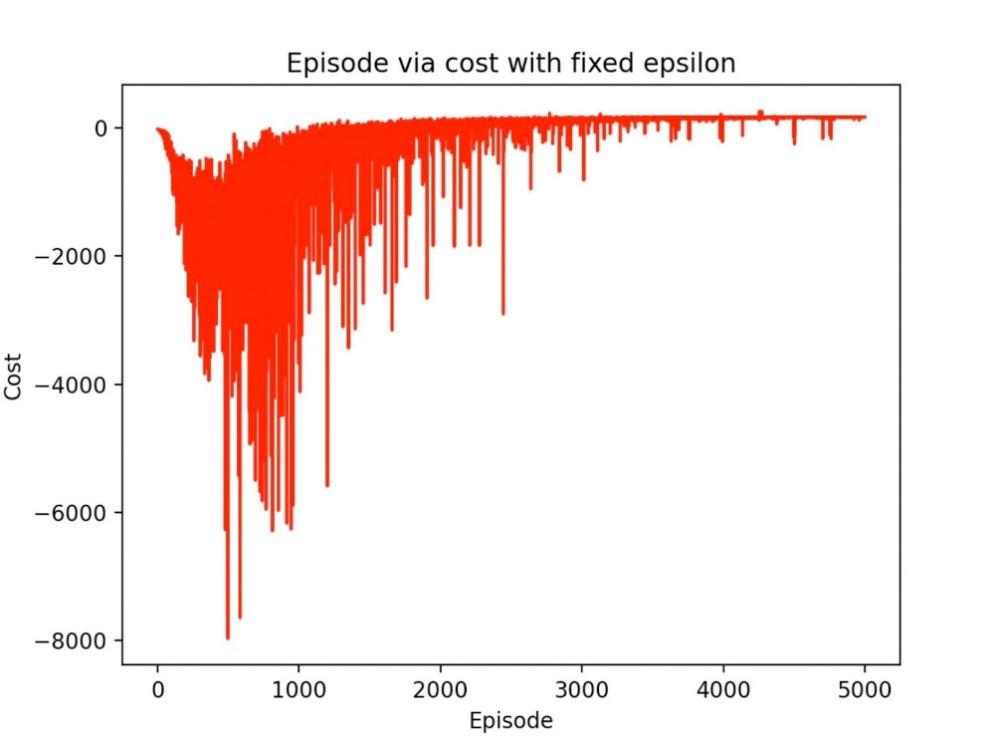
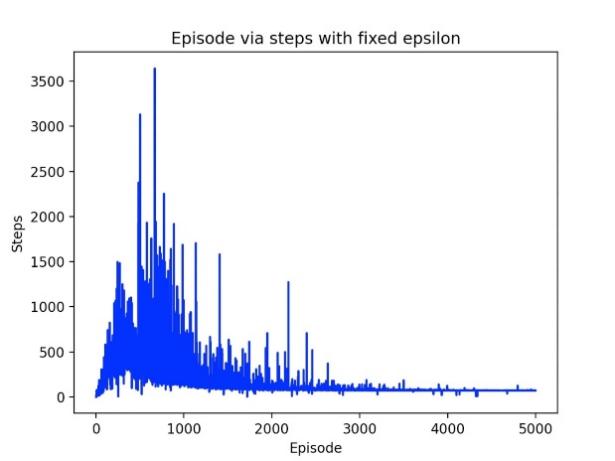
For the fixed epsilon experiment, we used factors of 0.95, 0.9 and 0.85 respectively, as shown in Figure 1-3. The figure below shows the optimal junction of 0.9. It can be seen that for cost, the maximum cost is about 8000, and the results begin to converge after 3000 epides. For steps, the maximum step is around 3600, and the convergence starts around epiode=3000. For the final Q-learning path result, the number of turns of the agent is 37, the shortest route=71, and the longest route=3689. The experiments were repeated for 10 times for different epsilons. For the fixed epsilon greedy q-learning algorithm, the average number of turns of the agent was 43.5, the shortest path was 71, and the average longest path was 2620.
|
Figure 2. Episode via cost with fixed episode. |
|
Figure 3. Episode via step with fixed episode. |
4.2. Experiment 2
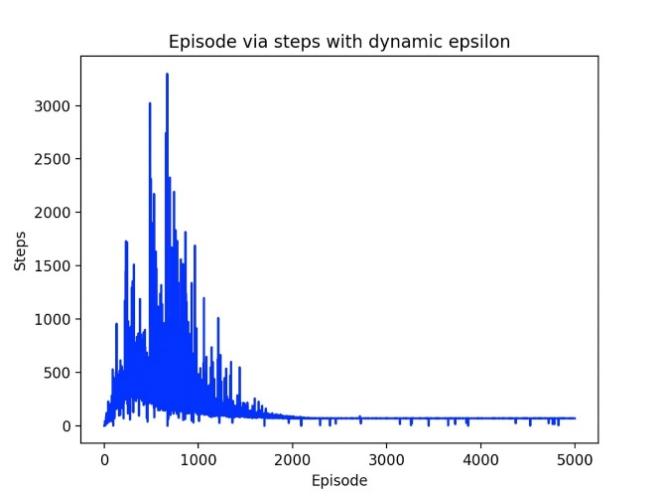
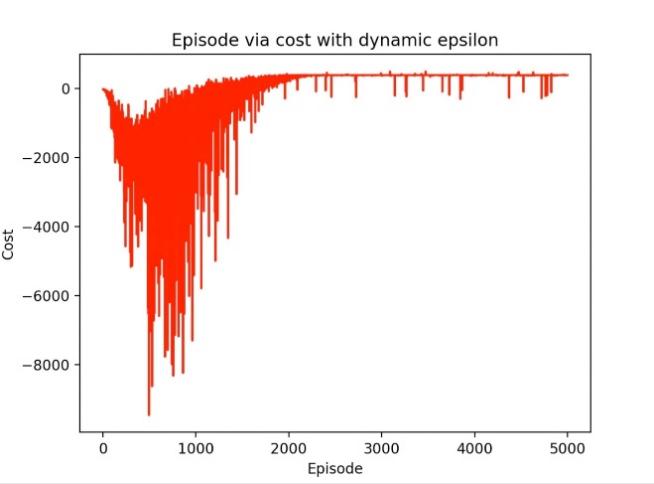
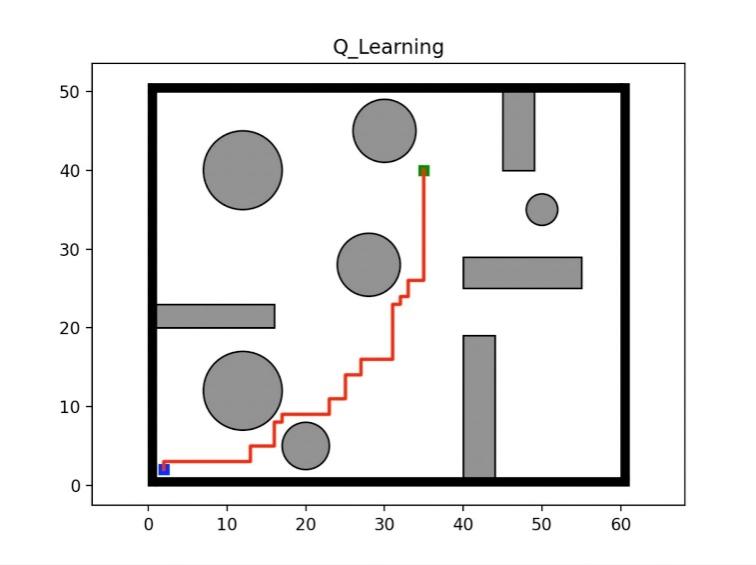
Through the dynamic epsilon experiment, we first set epsilon=0.95, 0.9, 0.85 to start the experiment. With the increase of the number of training iterations, epsilon gradually decreases. As shown in Figure 3-4, the maximum cost for cost is about 9500. After 2000 epides, the results begin to converge. For steps, the maximum step is around 3300, and the convergence starts around epiode=1800. For the final Q-learning path result, the number of agent turns is 15, the shortest route is 71, and the longest route is 1359. Another experimental result is also shown in the figure below when the path action=21 is selected. 10 experiments were conducted on different epsilons. For the dynamic epsilon greedy Q-learning algorithm, the average number of turns of the agent is 19.3, the shortest path is 71, and the longest path is 1593.
|
|
Figure 4. Episode via cost with fixed episode and Episode via step with fixed episode. | |
|
|
Figure 5. Path planning diagram2. | |
5. Conclusion
In order to reduce and improve the efficiency of path planning, enable robots to adapt to autonomous planning in different environments, and have the same autonomous learning and decision-making capabilities as humans, this paper uses the Q-learning algorithm in reinforcement learning to plan the path in complex and unknown environments, based on the traditional ε- The fixed factor epsilon is adopted by the greedy search strategy. This paper proposes a dynamic ε- Greedy search strategy can accelerate the path planning speed of the mobile robot, reduce the number of turns of the robot, improve the stability of the robot, and can be better applied to the transportation of mobile robots in the field of hazardous chemicals. However, with the dynamic decrease of epsilon in the experiment, there may be an unstable problem of agent early search, which needs further research and exploration.
References
[1]. Ko M H, Ryuh B S, Kim K C, et al. Autonomous greenhouse mobile robot driving strategies from system integration perspective: Review and application[J]. IEEE/ASME Transactions On Mechatronics, 2014, 20(4): 1705-1716.
[2]. Zhang J, Zhang F, Liu Z, et al. Efficient path planning method of USV for intelligent target search[J]. Journal of Geovisualization and Spatial Analysis, 2019, 3(2): 1-9.
[3]. Buniyamin N, Ngah W W, Sariff N, et al. A simple local path planning algorithm for autonomous mobile robots[J]. International journal of systems applications, Engineering & development, 2011, 5(2): 151-159.
[4]. Ouyang H, Chen X. 3D meso-scale modeling of concrete with a local background grid method[J]. Construction and Building Materials, 2020, 257: 119382.
[5]. Shelokar P S, Siarry P, Jayaraman V K, et al. Particle swarm and ant colony algorithms hybridized for improved continuous optimization[J]. Applied mathematics and computation, 2007, 188(1): 129-142.
[6]. Kaveh A, Talatahari S. Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures[J]. Computers & Structures, 2009, 87(5-6): 267-283.
[7]. Pan C, Wang H, Li J, et al. Path planning of mobile robot based on an improved ant colony algorithm[C]//International Conference on Convergent Cognitive Information Technologies. Springer, Cham, 2018: 132-141.
[8]. Mendel J M, McLaren R W. 8 reinforcement-learning control and pattern recognition systems[M]//Mathematics in science and engineering. Elsevier, 1970, 66: 287-318.
[9]. Alagoz O, Hsu H, Schaefer A J, et al. Markov decision processes: a tool for sequential decision making under uncertainty[J]. Medical Decision Making, 2010, 30(4): 474-483.
[10]. Sharma S, Sood Y R, Sharma N K, et al. Modeling and sensitivity analysis of grid-connected hybrid green microgrid system[J]. Ain Shams Engineering Journal, 2022, 13(4): 101679.
Cite this article
Lin,J. (2023). Path planning based on reinforcement learning. Applied and Computational Engineering,5,853-858.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Signal Processing and Machine Learning
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Ko M H, Ryuh B S, Kim K C, et al. Autonomous greenhouse mobile robot driving strategies from system integration perspective: Review and application[J]. IEEE/ASME Transactions On Mechatronics, 2014, 20(4): 1705-1716.
[2]. Zhang J, Zhang F, Liu Z, et al. Efficient path planning method of USV for intelligent target search[J]. Journal of Geovisualization and Spatial Analysis, 2019, 3(2): 1-9.
[3]. Buniyamin N, Ngah W W, Sariff N, et al. A simple local path planning algorithm for autonomous mobile robots[J]. International journal of systems applications, Engineering & development, 2011, 5(2): 151-159.
[4]. Ouyang H, Chen X. 3D meso-scale modeling of concrete with a local background grid method[J]. Construction and Building Materials, 2020, 257: 119382.
[5]. Shelokar P S, Siarry P, Jayaraman V K, et al. Particle swarm and ant colony algorithms hybridized for improved continuous optimization[J]. Applied mathematics and computation, 2007, 188(1): 129-142.
[6]. Kaveh A, Talatahari S. Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures[J]. Computers & Structures, 2009, 87(5-6): 267-283.
[7]. Pan C, Wang H, Li J, et al. Path planning of mobile robot based on an improved ant colony algorithm[C]//International Conference on Convergent Cognitive Information Technologies. Springer, Cham, 2018: 132-141.
[8]. Mendel J M, McLaren R W. 8 reinforcement-learning control and pattern recognition systems[M]//Mathematics in science and engineering. Elsevier, 1970, 66: 287-318.
[9]. Alagoz O, Hsu H, Schaefer A J, et al. Markov decision processes: a tool for sequential decision making under uncertainty[J]. Medical Decision Making, 2010, 30(4): 474-483.
[10]. Sharma S, Sood Y R, Sharma N K, et al. Modeling and sensitivity analysis of grid-connected hybrid green microgrid system[J]. Ain Shams Engineering Journal, 2022, 13(4): 101679.