1. Introduction

Robotic manipulators are widely used in industry, health care, agriculture, and other industries. Handling and storing the payload is one of the significant operations dispelled using a robotic manipulator [1]. However, their operation environment is often complex, with dynamic obstacles such as moving personnel and vehicles constantly present. A significant challenge in robotics is ensuring that robot manipulators can avoid these dynamic obstacles in real-time while maintaining high-efficiency operation. In manual control, the operator performs all tasks except low-level position control. This requirement posits a significant cognitive demand on the operator [2].

Traditional obstacle-avoidance methods for robots mainly include methods based on Artificial Potential Fields, Cell Decomposition, Visibility graphs, Voronoi Diagrams, and Probabilistic Road Maps [3]. Although these methods have achieved specific results in static or semi-static environments, they face difficulties in dynamic and complex scenarios. For example, artificial potential field methods may encounter problems such as target inaccessibility and local minima, often requiring many computational resources for real-time dynamic obstacle detection and path planning [4].

On the contrary, the SAC algorithm possesses numerous advantages. One of the most significant advantages is that the SAC algorithm, employing a stochastic strategy, demonstrates enhanced robustness and superior adaptability, rendering it particularly apt for addressing the challenges inherent in path-planning tasks [5].

This paper focuses on the dynamic obstacle-avoidance problem of robot manipulators in automated factories.

The simulation uses the URDF model of an open-source robotic arm to build a robot model in Python. Subsequently, the SAC algorithm in Python is applied to conduct dynamic obstacle avoidance trajectory planning for the constructed robot model. Through simulation simulations, the effectiveness and superiority of the proposed method in complex dynamic environments were verified, providing a new solution for the safe and efficient operation of the robot's operating arm in automated factories. In summary, the main contributions of this work are:

• A new dynamic obstacle avoidance and trajectory planning framework has been proposed: This framework combines the RRT algorithm for global path planning and the SAC algorithm for local path optimization to adapt to changes in a complex dynamic environment. This method addresses issues encountered by traditional obstacle avoidance methods, such as target inaccessibility and local minima.

• A Python-based URDF model of an open-source robotic arm has been constructed: This model has been applied to dynamic obstacle avoidance trajectory planning based on the SAC algorithm, thereby validating the effectiveness and superiority of the proposed method in complex and dynamic environments.

• An improved learning mechanism has been introduced: By adjusting the temperature parameter α in the SAC algorithm, the level of exploratory randomness is controlled, allowing the robotic arm to be more flexible in dealing with moving obstacles and achieving efficient trajectory planning.

The rest of the paper is organized as follows: Section II reviews the related work, focusing on the advantages of the RRT algorithm for high-dimensional path planning and the SAC algorithm's capability in managing continuous action spaces. Section III details our proposed framework for dynamic obstacle avoidance and trajectory planning, covering the design aspects of state space, action space, and reward function composition. Section IV describes the simulation setup using the PyBullet physics engine to demonstrate trajectory optimization and obstacle avoidance, along with an analysis of the training outcomes. Finally, Section V summarizes the findings, highlighting the method's effectiveness and practical potential while acknowledging its limitations and suggesting future research directions.

2. Related work

This paper proposes a trajectory planning framework that integrates the RRT and SAC algorithms for efficient and stable dynamic motion generation [6].

RRT achieves an \( O(nlogn) \) computational complexity in high-dimensional global path planning, outperforming deterministic algorithms with exponential complexity [7]. This efficiency is attributed to its probabilistic sampling mechanism, which ensures asymptotic completeness and minimizes the exploration space [8]. The algorithm can perform a random sampling of points in the configuration space. For each sampling point, collision detection is performed to verify whether the path from the nearest node in the tree to this sampling point is collision-free. If there is no collision along the path, add this sampling point to the tree, thereby gradually constructing the path from the starting point to the destination [9]. The algorithm flowchart is presented in Fig.1

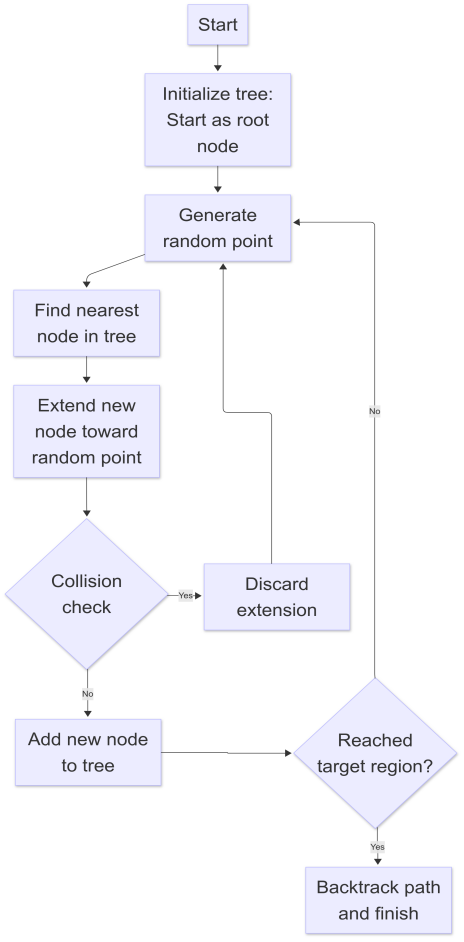
Figure 1: RRT algorithm flowchart

Furthermore, SAC is integrated into the framework for local trajectory refinement to address dynamic path adaptation [10]. SAC is a maximum-entropy deep reinforcement learning algorithm well-suited for continuous action spaces [11]. It balances exploration and exploitation through a stochastic policy network and twin Q - networks. Entropy regularization and target network updates enable SAC to effectively handle high-dimensional state-action spaces [12]. In robotic manipulator trajectory planning, SAC dynamically adjusts the temperature parameter α to control exploration randomness, thereby enhancing real-time adaptability, which allows the robotic arm to navigate complex environments with moving obstacles and achieve efficient trajectory planning [13].

The RL mainly includes three sections: policy, function, and model. The policy decides what the intelligent will do next, while the function predicts the future reward and the model determines the following status [14].

The actor network is responsible for choosing the action and managing exploration for the SAC algorithm. At the same time, the critic network interacts with the working environment and predicts the value functions of each step [15]. An entropy regulation is included in the SAC algorithm, which encourages the agent's exploration [16]. This maximum entropy ensures that the policy network can get the maximum reward and, as a result, optimize the trajectory. It has now been widely used in robotic arms. The flowchart of the SAC algorithm is shown in Fig. 2.

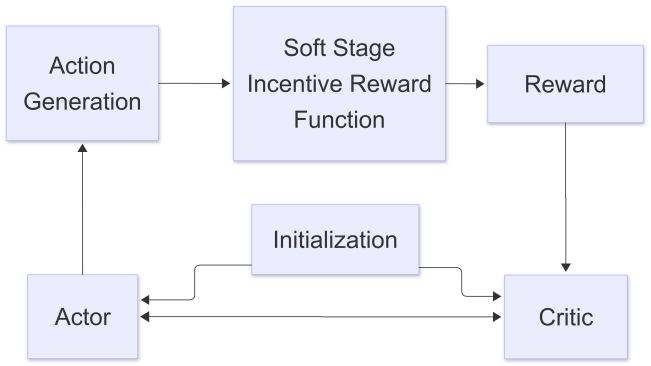
Figure 2: SAC algorithm flowchart

The object function can be expressed as in formula (1):

\( \underset{π}{max}{{E_{τ~π}}[\sum _{t=0}^{T}{γ^{t}}R({s_{t}}, {a_{t}})]}+{E_{a~π}}[H(π(a|s))] \) (1)

where \( \underset{π}{max}{{E_{τ~π}}[\sum _{t=0}^{T}{γ^{t}}({s_{t}}, {a_{t}})]} \) is the expected return in the RL. The agent maximizes the discounted sum of reward, which is the discount factor that determines how much future rewards influence decision-making. The entropy of policy \( π(a|s) \) encourages stochasticity in action selection. The entropy function \( H(π) \) ensures that the policy does not become too deterministic, improving exploration and stability during training.

3. Problem formulation

3.1. State space & action space

The state space of the robotic arm comprises three parts: the joint angles, time information, and obstacle positions. A 7-degree-of-freedom (7-DOF) robot from the PyBullet library was utilized, and two sphere obstacles were defined to move in straight lines at identical speeds but in opposite directions. The dimensions of the three parts are presented respectively in Table 1.

Table 1: State space

The seven joint angles are limited to a specific range. Time is normalized as shown in formula (2):

\( \frac{{t_{current}}}{{t_{max}}} \) (2)

where \( {t_{current }} \) is the current time, and \( { t_{max }} \) stands for the maximum time of one episode. Each obstacle has three position dimensions, and the total dimensionality of the obstacles is 6.

The action space includes all possible movements of the agent, and the action ranges from (-1,1) for all seven angles. It has seven dimensions in total. Furthermore, actions were clipped to limit the working space, and a normal distribution was added to the action to simulate random noise in real environments, as presented in the formula (3):

\( \hat{a}=max(min(a,1),-1) ×0.5+N(0,0.1) \) (3)

The term \( max(min(a,1),-1) \) ensures that the original action \( a \) is limited to the range (-1,1), where actions were clipped to 50% of their original values, and a normal distribution with a mean of 0 and a standard deviation of 0.1 was added to simulate noise in real-world industrial environments.

3.2. Reward function

This section designs the reward function in multiple ways. Overall, the reward function can be expressed as the sum of multiple kinds of reward functions:

\( {R_{total}}= \sum {R_{i}} \) (4)

where \( {R_{i}} \) represents the following reward functions.

For the orientation function, the reward function is shown in an exponential form in (5):

\( {R_{position}}=\begin{cases} \begin{array}{c} 200×exp({-D_{PT}}×10) {D_{PT}} \gt 0.2 \\ 200×exp({-D_{PT}}×10)+\frac{25}{{D_{PT}}} { D_{PT}}≤0.2 \end{array} \end{cases} \) (5)

where \( {D_{PT}} \) is the distance between the target and the end effector. After the distance is not higher than 0.2, we added another term \( {25/D_{PT}} \) to guide the agent to the target.

To guide the robotic arms to the target direction, a direction vector was employed, which is shown as (6):

\( {R_{direction}}= 2×clip(({p_{target}}-{p_{ee}})∙{n_{link}},-2, 2) \) (6)

where \( {p_{target }}, {p_{ee}} \) stand for target position and end effector position respectively. And \( {n_{link}} \) is the unit vector of the direction of the target. The clip function limits the range of \( ({p_{target}}-{p_{ee}})∙{n_{link}} \) to (-2,2).

Another reward function is designed to keep a safety distance away from the obstacles. \( {d_{1 }}, {d_{2}} \) stand for the distance between the target and the 2 obstacles. The function is shown as (7):

\( {R_{obstacle}}= \) ( \( -\frac{1}{1+|{d_{1}}|}- \frac{1}{1+|{d_{2}}|}) / 50 \) (7)

To ensure smoothness and natural joint configurations, a smoothness reward function and a posture reward function were utilized, which can be defined as equations (8) and (9):

\( {R_{smoothness}}=-|\hat{a}| \) (8)

\( {R_{posture}}=-\frac{‖{q_{pos}}‖ }{100} \) (9)

where \( |\hat{a}| \) is the action of the robotic arm after clapping.

\( {q_{pos}} \) stands for the array of 7 joint positions of the robotic arm.

Finally, an exploration reward function is added to encourage the exploration of the robotic arm. It is shown in the equation (10):

\( {R _{exploration}}=N(0 , 0.1) \) (10)

N(0,0.1) is a Gaussian random variable with mean 0 and standard deviation 0.1.

C. Collision detection

One of the most important tasks in this simulation is to imply obstacle avoidance in trajectory planning. Collision is determined by whether the distance between the obstacle and the nearest point of the robotic arm is below the threshold. The collision detection is shown in formula (11):

\( {|d|_{min}} \lt r+δ \) (11)

where \( {|d|_{min}} \) is the minimum distance between the robotic arms and obstacles and r is the radius of the two sphere obstacles. \( δ \) is the threshold, where it is set to 0.01 in this research.

4. Simulation

PyBullet is a powerful physics engine well-suited for robotic arm simulation. It offers various models to support diverse tasks across various scenarios [17].

The simulation uses PyBullet to optimize trajectory and obstacle avoidance via reinforcement learning. A simulation environment for a 7-DOF KUKA robotic manipulator was established. The training flowchart is presented in Fig.3.

Figure 3: Training flowchart of the simulation

First, the RRT algorithm generates a global path. Post global path generation, collision checking is executed. If a collision occurs, a negative reward is assigned. If no collision is detected, a check for goal attainment follows. A goal-reached reward is given when the goal is reached; if protection time elapses without goal attainment, the corresponding condition is processed. These reward calculations feed into the SAC reinforcement learning algorithm.

Specifically, after RRT generates the global path, the SAC algorithm optimizes the local path. SAC uses a stochastic policy network and twin Q-networks as a maximum-entropy deep reinforcement learning algorithm for continuous action spaces. Integrating entropy regularization and target network mechanisms balances exploration and exploitation. In robotic manipulator trajectory planning, the SAC algorithm dynamically adjusts the temperature parameter α to control policy exploration randomness, which enables the manipulator to autonomously optimize local paths according to the global path generated by RRT. The robotic manipulator, dynamic obstacles, and target points are instantiated during simulation environment initialization. The state space comprises joint angles, normalized time values, and obstacle positions, while the action space consists of joint angular velocity commands.

Throughout the training, with obstacles moving periodically along prescribed straight paths, the robotic manipulator learns strategies to reach targets while avoiding obstacles. Integrating RRT-based global path planning and SAC-based local path optimization enables the manipulator to handle dynamic obstacles and complex environments effectively, improving the target-reaching success rate.

After training, learning effectiveness is analyzed and visualized using reward curves, success-rate pie charts, action-range histograms, and robotic manipulator motion trajectories. This analysis validates the effectiveness of obstacle-avoidance strategies and target achievability [18].

5. Simulation results

In this section, simulations were conducted to evaluate the performance of the SAC algorithm integrated with RRT for trajectory planning. Comparative evaluations were also performed against other algorithms, such as DDPG (Deep Deterministic Policy Gradient). A slightly lower learning rate of 5*10^-5 is set instead of the default value of 3*10^-4 to encourage the agent's exploration and ensure more stable training. The batch size is enlarged to 512, and the buffer size is increased to 1*10⁷. Instead of using the 'auto' entropy coefficient, a fixed entropy rate of 0.1 is adopted to balance practical exploration and achieve a smoother convergence curve. The model is trained 100,000 times. If the distance between the end effector and the target is not higher than 0.1 after training, we define it as a successful trajectory.

The simulation compared the reward values and success rates in four scenarios: SAC with RRT, SAC without RRT, DDPG with RRT, and DDPG without RRT. The four reward curves, shown in Fig. 4, represent the trend of the reward values in these four conditions.

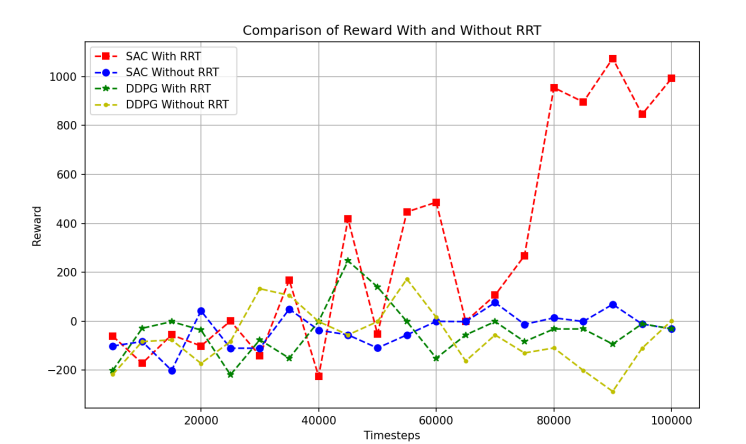
Figure 4: Reward progress of different algorithms

According to Fig.4., the reward value shows an increasing trend when we combine SAC with RRT. In contrast, the reward values of the other three situations remain stable after 100,000 timesteps, which supports the effectiveness of the combination of SAC and RRT under this reward function.

Fig.5 illustrates the trend of success rates in four situations. It can be concluded that when applying SAC and RRT together, the success rate rises dramatically to about 35% after 100,000 timesteps, while the other three scenarios only see a slight increase in success rates, from 0% to 5% after the robotic arm is trained 100,000 times. The success rate becomes much higher when adding RRT to the original SAC algorithm, indicating that this method performs better than all the other 3 conditions under this simulation environment.

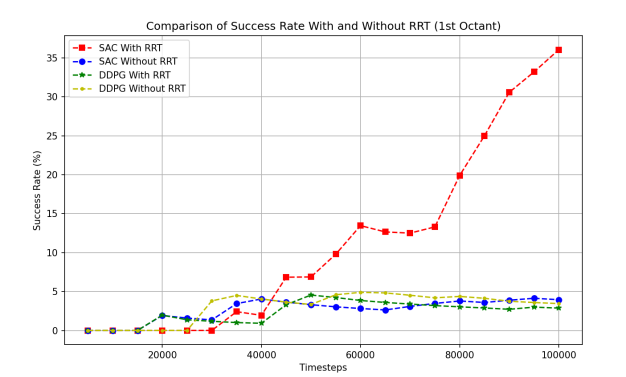
Figure 5: Success rates of different algorithms

Fig.6 and Fig.7 compare the trajectory of SAC and DDPG after training 100,000 timesteps, both with RRT. The SAC algorithm features a smoother and shorter path than DDPG. Both of the two algorithms can handle trajectory planning successfully. The SAC algorithm generates a smoother and more direct path, whereas the DDPG trajectory is more convoluted and time-consuming.

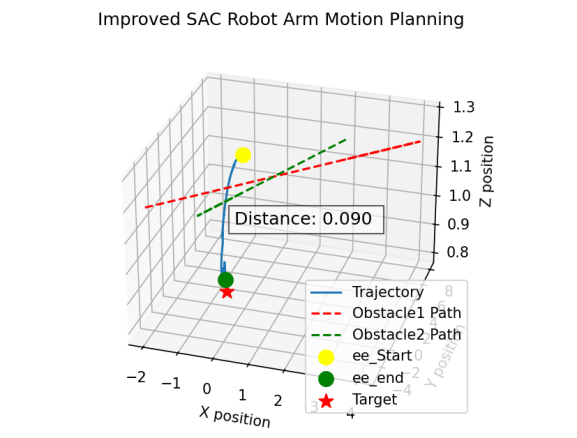
Figure 6: Trajectory of SAC algorithm after training

Figure 7: Trajectory of DDPG algorithm after training

All results and comparisons demonstrate that combining SAC with RRT leads to the most effective trajectory planning among the four conditions.

6. Conclusions

In conclusion, the effectiveness of the proposed method for dynamic obstacle avoidance and trajectory planning using the SAC algorithm was verified via simulations. The results show that our method can successfully navigate obstacles while efficiently reaching the target position. Compared with traditional algorithms such as artificial potential fields and geometric methods, our approach demonstrates significant advantages regarding adaptability to dynamic environments and computational efficiency.

One notable observation is the smoothness of the trajectories generated by our model. Thanks to the motion smoothness reward function, the robotic arm could move along more natural paths, which not only improved the stability of the operation but also reduced wear and tear on the mechanical components, which is particularly important in industrial settings where maintenance costs are a key concern.

However, some limitations were encountered during our simulations. For instance, the initial setup phase required careful tuning of parameters to achieve optimal performance. Additionally, while the SAC algorithm performed well in simulated environments, its real-world applicability remains to be tested. Future work will focus on implementing a more complex environment by adding additional obstacles and generating random obstacle paths to test and prove the effectiveness of our SAC algorithm.