1. Introduction

As an old special combination number, Catalan numbers are related to many kinds of combinatorial problems and other counting problems in mathematics. Its expression is as follows:

$$ \begin{array}{c}{C}_n=\frac{1}{n+1}\left(\genfrac{}{}{0pt}{}{2n}{n}\right)=\frac{\left(2n\right)!}{\left(n\right)!\left(n+1\right)!}\end{array}$$(1)

The most common Catalan numbers have many combinatorics interpretions like binary trees, triangulations, binary parenthesizations, plane trees, Dyck path, ballet sequence and so on. You can see more detailed applications in Stanley's lectures [1].

In 1915, MacMahen [2] firstly solved the n-ballot problem, and proposed the higher-dimension-Catalan numbers, and later in 1983, Zeilberger [3] solved this problem by a new algebraic combinatoarics way called the reflection principle. The expression they got is:

$$ \begin{array}{c}{C}_d\left(n\right)=\left(nd\right)!{\prod }_{i=0}^{d-1}\frac{i!}{\left(n+i\right)!}\end{array}$$(2)

The reflection principle mainly uses some properties between the symmetric group and its action on the Dyck path. The main lemma he got was:

$$ \begin{array}{c}\sum _{\pi \in even} B\left(e_{\pi }\to m\right)=\sum _{\pi \in odd} B\left(e_{\pi }\to m\right)\end{array}$$(3)

where  $$ \mathrm{\pi }$$  is a permutation,  $$ B\left(e_{\mathrm{\pi }}\to m\right)$$  is the path from  $$ e_{\mathrm{\pi }}$$  to  $$ m$$  which does not belong to the good one(or called dyck path), and  $$ e_{\mathrm{\pi }}$$  means the point  $$ \left(1-\mathrm{\pi }\left(1\right),2-\mathrm{\pi }\left(2\right),\dots ,n-\mathrm{\pi }\left(n\right)\right)$$ . In the article, Zeilberger used the lemma with some other transforms and finally got the results beautifully. We will review the details of his proof in the next sections.

Also, some other generalizations of Catalan numbers were proposed like q-Calatan numbers, which was introduced by Fürlinger and Hofbauer [4], using the idea of q-analogue:

 $$ {\left[n\right]}_q=\frac{1-q^n}{1-q}$$  , to get a more complex expression:

$$ \begin{array}{c}{C}_q\left(n\right)=\frac{1}{[n+1{]}_q}{\left[\begin{array}{c}2n\\ n\end{array}\right]}_q\end{array}$$(4)

It can be related to some more complex Dyck path problem and other counting problems.

Fuss-Catalan numbers is another generalization, which was proposed by Fuss in 1791 and Raney [5] later(which is much earlier than the formally proposing of Catalan numbers), its expression is as follows:

$$ \begin{array}{c}{C}_n^{\left(s\right)}=\frac{1}{\left(s-1\right)n+1}\left(\genfrac{}{}{0pt}{}{sn}{n}\right)\end{array}$$(5)

This kind of generalization is also related to some more restricted Dyck path, specifically, it counts the number of ways from  $$ \left(\mathrm{0,0}\right)$$  to  $$ \left(n,\left(s-1\right)n\right)$$ , which stays weakly below the line  $$ y=\left(s-1\right)x$$ . It can also be called as  $$ \left(n,\left(s-1\right)n\right)-dyck path$$ 

2. The main results

We may review the detailed proof of Zeilberger, and try to propose a new proof of the formula for the higher-dimension-Catalan numbers, also, give two generalizations of Catatlan numbers.

2.1. Zeilberger's proof

Like the introduction says, Zeilberger's proof mainly use the idea of permutation groups' action on the path  $$ \left(e_{\mathrm{\pi }}\to m\right)$$ ,  $$ e_{\mathrm{\pi }}$$  denoting the point  $$ \left(1-\mathrm{\pi }\left(1\right),2-\mathrm{\pi }\left(2\right),\dots ,n-\mathrm{\pi }\left(n\right)\right)$$ .

We will call a path from  $$ a$$  to  $$ b$$  is good if it never touches the hyperplane  $$ x_i-x_i+1=1$$ , and denote the set of good paths by  $$ G\left(a\to b\right)$$ , while we call the others bad one, denoted as  $$ B\left(a\to b\right)$$ .

Let us consider doing something to all the bad ones. If some path touches the hyperplane in their walk to the final point  $$ \left(m_1,m_2,\dots ,m_k\right)$$ , we need to reflect the path before the first touching point with respect to the hyperplane  $$ x_i-x_{i+1}=1$$ , and we claim that the reflection is well-defined. Since this progress is not written in the Zeilberger's article, so we decide to make a detailed description.

In order to get the reflection point of any point  $$ G$$  on the path, we could firstly find the point  $$ O$$  on the hyperplane  $$ P:x_i-x_i+1=1$$  such that  $$ \overrightarrow{OG}\perp P$$ . Assume  $$ O=\left(t_1,t_2,..,t_n\right)$$ , and denote  $$ x_{i+1}\left(O\right)=x$$ , then  $$ x_i\left(O\right)=x-1$$ . Then,  $$ \overrightarrow{OG}=\left(\dots ,x_i-\left(x-1\right),x_{i+1}-x,\dots \right)$$ , where "..." means any numbers. Since any point on the hyperplane can be written in  $$ O$$ 's form, we can assume that any vector on the this hyperplane has form of  $$ v=\left(y_1,\dots ,y_n\right)$$ , and  $$ v_i=v_{i+1}=y$$ . In order to satisfy the  $$ \overrightarrow{OG}\perp P$$  condition, the "..." in the  $$ \overrightarrow{OG}$$  must be all zero. And they need to satisfy the equality:  $$ \left(x_i-\left(x-1\right)\right)y+\left(x_{i+1}-x\right)y=0$$ , we can get  $$ x=\frac{x_i+x_{i+1}+1}{2}$$ . Then we just get the reflection point  $$ G^{\text{'}}=\left(x_1,..,x_{i+1}-1,x_i+1,..,x_n\right)$$ . Now, we get the well-defined reflection action, and the whole bad path from  $$ \left(1-\mathrm{\pi }\left(1\right),2-\mathrm{\pi }\left(2\right),\dots ,n-\mathrm{\pi }\left(n\right)\right)$$  turns into  $$ \left(1-\mathrm{\pi }\left(1\right),2-\mathrm{\pi }\left(2\right),..,i-\mathrm{\pi }\left(i+1\right),i+1-\mathrm{\pi }\left(i\right),..,n-\mathrm{\pi }\left(n\right)\right)$$ , since  $$ \mathrm{\pi }$$  is a permutation in  $$ S_n$$ , and the above reflection operation can be seen as adding a transposition  $$ \left(i i +1\right)$$ on it. Therefore, we get a bijection from an even permutation to an odd one, since the transposition changes the sign of permutation. Simply speaking, we get the following equality, just as said in the introduction:

$$ \begin{array}{c}\sum _{\pi \in even} B\left(e_{\pi }\to m\right)=\sum _{\pi \in odd} B\left(e_{\pi }\to m\right)\end{array}$$(6)

Let  $$ F\left(0\to m\right)$$  denote all the paths, we easily see that  $$ F\left(e_{\mathrm{\pi }}\to m\right)=B\left(e_{\mathrm{\pi }}\to m\right)$$ , since the point  $$ e_{\pi }$$  ( $$ \mathrm{\pi }$$  is not id) already exceeds some hyperplane.

While for any  $$ F\left(a\to b\right)$$ ,\  $$ a=\left(a_1,\dots ,a_n\right)$$  and  $$ b=\left(b_1,\dots ,b_n\right)$$ , it is well known that

$$ \begin{array}{c}F\left(a\to b\right)=\frac{\left(b_1+\dots +b_n-a_1-\dots -a_n\right)!}{\left(b_1-a_1\right)!\dots \left(b_n-a_n\right)!}\end{array}$$(7)

What we want to get is the number of  $$ G\left(0\to m\right)$$, let us calculate it by the above lemma.

$$$ \begin{array}{c}\begin{array}{c}G(0\to m)=F(0\to m)-B(0\to m)\\ =F\left(0\to m\right)-\left(\sum _{\pi \in odd} B\left(e_{\pi }\to m\right)-\sum _{\genfrac{}{}{0pt}{}{\pi \in \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}{\pi \ne \mathrm{i}\mathrm{d}}} B\left(e_{\pi }\to m\right)\right)\\ =\sum _{\pi \in S_n} (-1{)}^{\sigma \left(\pi \right)}F(e_{\pi }\to m)\\ =\sum _{\pi \in S_n} (-1{)}^{\sigma \left(\pi \right)}\frac{\left(m_1+\dots +m_n\right)!}{\left(m_1-1+\pi \left(1\right)\right)!\dots \left(b_n-n+\pi \left(n\right)\right)!}\\ =\left(m_1+\dots +m_n\right)!det\left(\frac{1}{\left(m_i-i+j\right)!}\right)\\ =\frac{\left(m_1+\dots +m_n\right)!}{\left(m_1+n-1\right)\dots m_n}\prod _{i=0}^{d-1} \left(m_i-m_j+j-i\right)!\end{array}\end{array}$$$(8)

The final step to calculate the determinant is a interesting exercise like the VanderMonde determinant.

2.2. Our new combinatorics proof

Definition: ordered Catalan numbers

Consider a sequence with  $$ dn$$  elements and  $$ A_1,A_2,\dots ,A_d$$  groups, every group has  $$ a_{k1},a_{k2},\dots ,a_{kn}$$  elements. Then we consider these two rules:

rule2.2.1.

We denote the numbers of elements in the first k elements from  $$ A_d$$  be  $$ N_d\left(k\right)$$ . Then if the sequence is an ordered Catalan numbers, it satisfies that  $$ N_1\left(k\right)\ge N_2\left(k\right)\ge N_3\ge \dots \ge N_d\left(k\right)$$  for all of the  $$ k$$  belongs to  $$ \mathrm{1,2},3,\dots ,n$$ .

rule2.2.2.

For the  $$ a_{k1},a_{k2},\dots ,a_{kn}$$  from the  $$ A_k$$  group, if  $$ i<j$$ , then  $$ a_i$$  must be before  $$ a_j$$ . And for the  $$ k, i$$  belonging to the  $$ \mathrm{1,2},\dots ,d$$ , if  $$ k<t$$ , then  $$ A_k$$  must be before the  $$ A_t$$ . Then we call the sequence that follows the two rules above the "ordered Catalan numbers" and we denote it as  $$ C_d^{\text{'}}\left(n\right)$$  then we have the lemma2.1.

Lemma2.1.

The ordered Catalan numbers satisfy that:  $$ C_d\left(n\right)=C_d^{\text{'}}\left(n\right)\times {\left(n!\right)}^d$$ 

Proof.For the d-dimensional Catalan numbers, it only needs to satisfy rule one and that the group  $$ A_1,A_2,\dots ,A_d$$  is arranged. Also, because in group  $$ A_k$$  we can choose any arrangement of  $$ a_{k1},a_{k2},\dots ,a_{kn}$$ , so we can get an arrangement that satisfies the rule of d-dimensional Catalan numbers, then we just get  $$ C_d\left(n\right)=C_d^{\text{'}}\left(n\right)\times {\left(n!\right)}^d$$ 

Let us calculate the  $$ C_d^{\text{'}}\left(n\right)$$ . It is easy to see that the arrangement of these  $$ n\times d$$  elements is  $$ \left(n\times d\right)!$$  and we call a process which makes the group  $$ A_1,A_2,\dots ,A_k$$  satisfy rule 1 and rule 2 as "operation k". Also, we denote that the ratio of all qualified permutations before operation k to all qualified permutations after operation k is  $$ R_k$$ , then  $$ C_d^{\text{'}}\left(n\right)=\left(dn\right)!\times {\prod }_{i=1}^d\left(R_i\right)$$ .

We claim that  $$ R_1=\frac{1}{n!}$$ ,  $$ R_k=\frac{\left(k-1\right)!}{\left(n+k-1\right)!n!}$$  for  $$ k\ge 2$$ . Firstly for  $$ R_1$$ , it's obviously that in the  $$ n!$$  permutations, there is only one satisfying the rule 2. We only need to consider  $$ A_1$$ , while it obviously satisfies the rule 1, hence  $$ R_1=\frac{1}{n!}$$ . Let us prove the condition for  $$ k\ge 2$$  by induction. For  $$ k=2$$ , we can consider such method to make it satisfy the rule 1 and rule 2. Firstly consider the first element in  $$ A_1$$  which is  $$ a_{11}$$  and the n elements in  $$ A_2$$  which are  $$ a_{21},a_{22},\dots ,a_{2n}$$ , according to rule 1, the  $$ a_{11}$$  must be before all of the elements in  $$ A_2$$ .Additionally, for the  $$ a_{21},a_{22},\dots ,a_{2n}$$ , there is only one arrangement which satisfies the rule 2. So, for the  $$ n+1$$  elements, there is only one qualified arrangement. Then consider the  $$ a_{12},a_{13},\dots ,a_{1n}$$  and  $$ a_{21},a_{22},a_{23},\dots ,a_{2n}$$ , for these  $$ 2n-1$$  elements, we need to find out the ratio of the qualified permutations to all permutations, thus we have lemma2.2.

lemma2.2.

Let's consider all of the permutations of  $$ 2n$$  elements, with n elements from group  $$ A_k$$  and n elements from  $$ A_{k+1}$$ . Suppose  $$ N_1$$  is the number of all possible permutations that satisfy the rule2.2.1,  $$ N_2$$  is the number of permutations that satisfy the condition that there is at least one element of the group  $$ A_k$$  lies before the elements of the group  $$ A_{k+1}$$ . Suppose  $$ \mathrm{ϵ}$$  equals  $$ \frac{N_1}{N_2}$$ , then we claim that  $$ \mathrm{ϵ}=\frac{1}{n!}$$ .

proof.

Let us prove it by gap filling method. Firstly, we denote the elements from group  $$ A_k$$  as  $$ a$$  and the elements from the group  $$ A_{k+1}$$  as  $$ b$$ . Because the permutations satisfy that before all of the elements from  $$ A_{k+1}$$ , there is at least one elements from  $$ A_k$$ , so we only need to consider such a sequence:  $$ a ,b,b,b\dots ,b$$  with an  $$ a$$  followed by n  $$ b$$ . And for the rest of the n-1  $$ a$$ , we just need to insert them into this sequence, and we can get the number of all possible permutations satisfying before all the  $$ b$$  there is at least one  $$ a$$  is  $$ N_0$$ = $$ {\prod }_{i=2}^n\left(n+i\right)$$ , and the numbers of the permutations satisfy the rule 1 is the Catalan numbers in two dimensions, which is  $$ N_1$$ = $$ \frac{\left(2n\right)!}{n!\left(n+1\right)!}$$ . So we just get the ratio is  $$ \frac{N_1}{N_0}$$ = $$ \frac{1}{n!}$$ .

Let's return to the original problem. Because the elements in the  $$ A_1$$  and  $$ A_2$$  has been arranged to follow rule 2, we can ignore the order relation of the elements in the group. Because the  $$ a_{11}$$  is before the  $$ a_{21},a_{22},\dots ,a_{2n}$$ , so before the elements from the group  $$ A_2$$  there is at least one elements from  $$ A_1$$ . Hence we can use Lemma2.2 and we can find out that for the sequence  $$ a_{12},a_{22},\dots ,a_{1n}$$  and  $$ a_{21},a_{22},\dots ,a_{2n}$$ , the qualified permutations to the possible permutations is  $$ \frac{1}{n!}$$ . By the analysis above, we can get that  $$ R_2=\frac{1!}{\left(n+1\right)!n!}$$  satisfy the formula  $$ R_k=\frac{\left(k-1\right)!}{\left(n+k-1\right)!n!}$$ .

And then we suppose that  $$ R_i$$   $$ i\le l$$  satisfies the formula. I'd like to show that the  $$ R_{l+1}$$  also satisfy the formula.

Because the sequence  $$ A_1,A_2,\dots ,A_l$$  has been arranged to satisfy the rule 1 and rule 2, so for the rule 1, we only need to make sure that  $$ N_l\left(k\right)\ge N_{l+1}\left(k\right)$$ , so the first elements of the group  $$ A_l$$  should before all of the elements of the  $$ A_{l+1}$$ . Because the the first  $$ l$$  groups satisfy the rule 1, the first element of the  $$ A_i$$  should before all of the elements of  $$ A_j$$  if  $$ i<j$$ . Hence the order of the elements of the first  $$ l$$  groups should be  $$ a_{11},a_{21},\dots ,a_{l1}$$ .

Now let us consider the elements of the first elements of the first  $$ l$$  groups and the n elements from the group  $$ A_{l+1}$$ . Because in all of the arrangements of these  $$ n+l$$  elements has only one qualified and the first elements of the first  $$ l$$  groups has been arranged, so the ratio of qualified arrangements to the all possible arrangements is  $$ \frac{\left(l\right)!}{\left(n+l\right)!}$$ . While for the rest  $$ a_{l,2},a_{l,3},\dots ,a_{l,n}$$  and  $$ a_{l+\mathrm{1,1}},a_{l+\mathrm{1,2}},\dots ,a_{l+1,n}$$ , the ratio of the qualified arrangements to the possible arrangements of these  $$ 2n-1$$  elements, according to lemma 2.2, is  $$ \frac{1}{n!}$$ .

Therefore,  $$ R_{l+1}$$ = $$ \frac{\left(l\right)!}{\left(n+l\right)!}\times \frac{1}{n!}$$  = $$ \frac{\left(l\right)!}{\left(n+l\right)!n!}$$ .

Then, because we have  $$ C_d^{\text{'}}\left(n\right)=\left(dn\right)!\times {\prod }_{i=1}^d\left(R_i\right)$$ ,  $$ C_d^{\text{'}}\left(n\right)=\left(dn\right)!{\left(\frac{1}{n!}\right)}^{d{\prod }_{i=1}^d\frac{\left(i-1\right)!}{\left(n+i-1\right)!}}$$ . With the relationship between ordered Catalan numbers and the d-dimensional Catalan numbers, we get the formula of d-dimensional Catalan numbers:

$$ \begin{array}{c}{C}_d\left(n\right)=\left(nd\right)!{\prod }_{i=0}^{d-1}\frac{i!}{\left(n+i\right)!}\end{array}$$(9)

2.3. Combination of two kinds of Catalan numbers

What we try to do in this section is to combine the Fuss-Catalan numbers and higher-dimension Catalan numbers. The Fuss-Catalan number has the form:

$$ \begin{array}{c}{C}_n^{\left(s\right)}=\frac{1}{\left(\left(s-1\right)n+1\right)}\left(\genfrac{}{}{0pt}{}{sn}{n}\right)\end{array}$$(10)

This number can be interpreted as: the path from  $$ \left(\mathrm{0,0}\right)$$  to  $$ \left(n,\left(s-1\right)n\right)$$  under the line  $$ y=\left(s-1\right)x$$ , a generalization of usual Dyck path. We have found an article written in Chinese [6], which considers Fuss-Catalan numbers for high-dimensional paths. The article presents the story in 3-dimensions. For the restriction:

$$ \left(s-1\right)y\ge z$$

$$ sx \ge y+z$$(11)

it can be seen that the path from  $$ \left(\mathrm{0,0},0\right)$$  to  $$ \left(n,n,\left(s-1\right)n\right)$$  is  $$ C_n^{\left(s\right)}\times C_n^{\left(s+1\right)}$$ . Since each path can be first projected to the  $$ yz$$ -plane, and the number of paths in this plane is just the original Fuss-Catalan numbers:  $$ C_n^{\left(s\right)}$$ , and then cut the path along the  $$ x$$  direction, it can be seen as the original path of the Fuss-Catalan numbers  $$ C_n^{\left(s+1\right)}$$ .

The following is a visual picture about the above proof of the three-dimensional restricted Fuss-Catalan numbers:

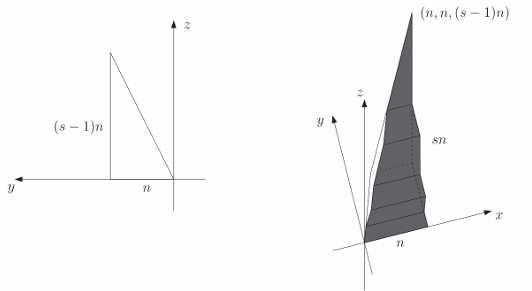
We may naturally consider the high-dimensional cases as the three-dimensional one. We will first consider the four-dimensional case for simplicity.

Consider the path from  $$ \left(\mathrm{0,0},\mathrm{0,0}\right)$$  to  $$ \left(n,n,n,\left(s-1\right)n\right)$$  in  $$ \left(x,y,z,t\right)$$  with the restriction that:

$$ \left(s-1\right)z\ge t$$

$$ sy \ge z+t$$(12)

$$ \left(s+1\right)x\ge y+z+t$$

We may just project the  $$ \left(x,y,z,t\right)$$  to  $$ \left(0,y,z,t\right)$$ , then the number of paths satisfying the condition in  $$ y,z,t-hyperplane$$  just equals to the above 3-dimensional case,

 $$ C_n^{\left(s\right)}\times C_n^{\left(s+1\right)}$$ . Then we cut the path along the  $$ x$$ -directions, it is easy to see that the number of ways is just  $$ C_n^{\left(s+2\right)}$$ , so the whole number is  $$ C_n^{\left(s\right)}\times C_n^{\left(s+1\right)}\times C_n^{\left(s+2\right)}$$ .

Therefore, for d-dimensional case,  $$ \left(x_1,x_2,\dots ,x_d\right)$$ ,  $$ d \ge 4$$  and  $$ s \ge 2$$ , paths from  $$ \left(\mathrm{0,0},\dots ,0\right)$$  to  $$ \left(n,n,\dots ,\left(s-1\right)n\right)$$  with the condition:

$$ \left(s-1\right)x_{d-1}\ge x_d$$

$$ s{x}_{d-2}\ge x_{d-1}+x_d$$(13)

$$ \dots $$

$$ \left(s+d-3\right)x\ge x_2+x_3+\dots +x_d$$

the number is just  $$ {\prod }_{i=0}^{d-2}{C}_n^{\left(s+i\right)}={\prod }_{i=0}^{d-2}\frac{1}{\left(s+i-1\right)n+1}\left(\genfrac{}{}{0pt}{}{\left(s+i\right)n}{n}\right)$$ .

Besides, we are also interested in the ratio between higher-dimension Catalan numbers and the above higher-Fuss-Catalan numbers.

And for simplicity, we firstly see the  $$ s=2$$  case in three dimensions. Let  $$ R$$  denote their ratio.

$$ R=\frac{C_3^{\left(n\right)}}{C_n^{\left(2\right)}}$$

=$$ \frac{\left(3n\right)!\frac{2}{n!\left(n+1\right)!\left(n+2\right)!}}{\frac{1}{n+1}\left(\genfrac{}{}{0pt}{}{2n}{n}\right)\frac{1}{2n+1}\left(\genfrac{}{}{0pt}{}{3n}{n}\right)}$$(14)

= $$ \frac{2\left(2n+1\right)}{n\left(n+1\right)}$$

It's clear that as  $$ n \to \mathrm{\infty }$$ , the ratio  $$ R \to 0$$ . Also, in the n-dimensional case, the ratio will go to 0 as  $$ n \to \mathrm{\infty }$$ .

2.4. A generalization for the coefficient of Fuss-Catalan numbers

For the Fuss-Catalan numbers, we consider the condition that  $$ N_1\left(k\right)\times \mathrm{\lambda }\ge N_2$$  (just like the above passages told, we denote the numbers of elements in the first k elements from  $$ A_d$$  be  $$ N_d\left(k\right)$$ ) and we call the  $$ \mathrm{\lambda }$$  as the coefficient of Fuss-Catalan numbers. According to the definition of the coefficient of Fuss-Catalan numbers  $$ C_n^{\left(s\right)}$$ , we can find that  $$ \mathrm{\lambda }=s-1$$ . For the usual Fuss-Catalan number  $$ C_n^{\left(s\right)}$$ ,  $$ s$$  is always a integer. We may consider to generalize it into real numbers.

Firstly, let us consider a variant type of the counting problem for Fuss-Catalan numbers: we can consider the paths on a Cartesian plane, start from the point  $$ \left(\mathrm{0,0}\right)$$  and move to the point  $$ \left(n,nm\right)$$ ,  $$ n,m$$  are integers and the paths should follow two rules below :

Rule2.4.1.

We can only move one unit of distance in the  $$ x$$  or  $$ y$$  direction at a time.

Rule2.4.2.

All of the paths shouldn't go above the line that passes through the point (0,0) with slope  $$ \mathrm{\lambda }$$ . We call this line a restriction line.

According to the definition that  $$ N_1\left(k\right)\times \mathrm{\lambda }\ge N_2\left(k\right)$$ , we can see that the numbers of the paths satisfy the two rules is the Fuss-Catalan numbers that with the total elements for  $$ N_1$$  is  $$ n$$  and the total elements for  $$ N_2$$  is  $$ n\times m$$  with the coefficient  $$ \mathrm{\lambda }$$ .

We claim that, for  $$ {\mathrm{\lambda }}^{\text{'}}\in \left[m,\frac{mn-\mathrm{\lambda }+1}{n-1}\right)$$ ,  $$ C_{\mathrm{\lambda }=m,x=n,y=mn}=C_{{\mathrm{\lambda }}^{\text{'}},x=n,y=mn}$$  where  $$ C_{\mathrm{\lambda }=m,x=n,y=nm}$$  means move n steps in  $$ x$$  direction in total and move nm steps in  $$ y$$  direction in total and under the restriction line with slope  $$ m$$ .

We can notice that the numbers of the qualified paths only depend on the integer point under the restriction line, the numbers of the paths changes if and only if the change of restriction line adds or mines the integer point, so we are interested in the coordinate of the first added integer point as the slope of the restriction line increases. We claim that the coordinate of the first added point is  $$ \left(n-1,nm+1-m\right)$$ .

For the proof, we consider drawing all the lines with the same slope as  $$ y = mx$$ , but start from the point  $$ \left(\mathrm{0,1}\right),\left(\mathrm{0,2}\right),\dots ,\left(0,nm-1\right)$$, which is one step up to the below one, like the following figure:

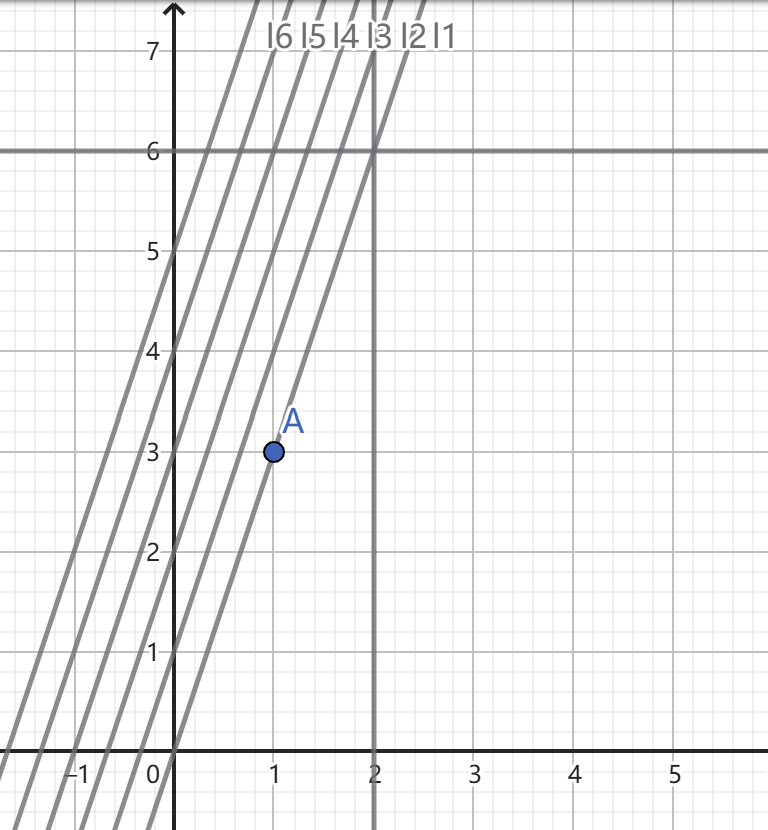
It is clear that there are no integer points between adjoint two lines, so for all the integer points beyond the  $$ l_1$$  in the same line, as the  $$ x$$  become bigger, the slope between the point and the start point will be smaller. So, we just need to avoid adding the last integer point  $$ x=\left(n-1,mn-\mathrm{\lambda }+1\right)$$  on the  $$ l_2$$ , which obviously guarantees that any lines will not add new points if its slope is smaller than  $$ \frac{mn-\mathrm{\lambda }+1}{n-1}$$ .

Therefore, we get the equality: $$ C_{\mathrm{\lambda }=m,x=n,y=mn}=C_{{\mathrm{\lambda }}^{\text{'}},x=n,y=mn}$$  if  $$ {\mathrm{\lambda }}^{\text{'}}\in \left[m,\frac{mn-\mathrm{\lambda }+1}{n-1}\right)$$ , since there are no new points added.

And now we may consider the case if  $$ {\mathrm{\lambda }}^{\text{'}}=\frac{mn-\mathrm{\lambda }+1}{n-1}$$ .

We can divide the path into two sorts: one goes through the point  $$ x=\left(n-1,mn-m+1\right)$$ , the other do not pass the added point. Then, it is easy to see that the number of paths passing  $$ x$$  is the Fuss-Catalan number  $$ C_{\mathrm{\lambda }=m,x=n-1,y=mn-\mathrm{\lambda }+1}$$ , because before we passes  $$ x$$ , we have to reach at the point  $$ \left(n-1,nm-m\right)$$  and the qualified paths from  $$ \left(\mathrm{0,0}\right)$$  to  $$ \left(n,nm-1\right)$$  is  $$ C_{\mathrm{\lambda }=m,x=n-1,y=nm-m}$$ . While we pass the point  $$ x$$ , there is only one way to the point  $$ \left(n,nm\right)$$ , so the numbers of the qualified paths which passes the point  $$ \left(n,nm+1-m\right)$$  is  $$ C_{\mathrm{\lambda }=m,x=n-1,y=nm-m}\times 1$$ . For the other case, it equals the original number  $$ C_{\mathrm{\lambda }=m,x=n,y=mn}$$ . Therefore, the whole number of this kind of generalization is

$$ \begin{array}{c}{C}_{\mathrm{\lambda }=\frac{mn-\mathrm{\lambda }+1}{n-1},x=n,y=mn}=C_{\mathrm{\lambda }=m,x=n-1,y=mn-m}+C_{\mathrm{\lambda }=m,x=n,y=mn}\end{array}$$(15)

This way, we have generalized the coefficient of the Fuss-Catalan numbers into a real numbers interval. Using the same method, if we can find the next added integer point, then we can generalize the coefficient into all of the positive real numbers.

3. Some corollaries and combinatorics

Catalan numbers have been shown to have a link with binary trees. We are now interested in the m-ary trees and some counting problems' bijection in m-analogue cases.

3.1. M-ary trees

The binary trees problem can be described as follows: How many different configurations are there for a binary tree with n nodes where each non-leaf node has exactly two children? The m-ary tree is similar to it.

We will finally find that the number of m-ary trees with n-node is just the Fuss-Catalan number:  $$ C_n^{\left(m\right)}$$ . The key of the proof is Raney’s lemma, and the following proof is leant from math.stackchange [7].

Lemma 3.1

If  $$ ⟨x_1,x_2,\dots ,x_m⟩$$  is any sequence of integers with  $$ x_k\le 1$$  for  $$ k=1,\dots , m$$  and with  $$ x_1+x_2+\dots +x_m=\mathrm{l}>0$$ , then exactly  $$ \mathrm{l}$$  of the cyclic shifts

$$ \begin{array}{c}⟨x_1,x_2,\dots ,x_m⟩,\hspace{0.25em}⟨x_2,\dots ,x_m,x_1⟩,\hspace{0.25em}\dots ,\hspace{0.25em}⟨x_m,x_1\dots ,x_{m-1}⟩\end{array}$$(16)

have all partial sums positive.

We may denote the  $$ C_n^{\left(m\right)}$$  be the number of  $$ m$$ -ary trees on  $$ n$$  nodes. Then it’s clear that

$$$ \begin{array}{c}{C}_{n+1}^{\left(m\right)}={\sum }_{k_1+\dots +k_m=n}{C}_{k_1}^{\left(m\right)}{C}_{k_2}^{\left(m\right)}\dots C_{k_m}^{\left(m\right)},\end{array}$$$(17)

while the  $$ k_1,\dots ,k_m$$  are the numbers of nodes in the  $$ m$$  subtrees hanging from the root node.

Now consider the set  $$ {\mathrm{\Sigma }}_n$$  of sequences  $$ ⟨x_0,\dots ,x_{mn}⟩$$  such that each  $$ x_k$$  is either  $$ 1$$  or  $$ 1-m$$ , each partial sum is positive, and the total sum is exactly  $$ 1$$ . Such a sequence has length  $$ mn+1$$ , so it must have exactly  $$ n$$  terms that are  $$ 1-m$$ . There are  $$ \left(\genfrac{}{}{0pt}{}{mn+1}{n}\right)$$  sequences of length  $$ mn+1$$  with  $$ n$$  terms equal to  $$ 1-m$$  and the rest equal to  $$ 1$$ . If we call two such sequences *equivalent* if they are cyclic shifts of each other, each equivalence class contains  $$ mn+1$$  sequences, and the lemma 3.1 implies that exactly one of them has all partial sums positive. Thus,

$$ \begin{array}{c}\left|{\mathrm{\Sigma }}_n\right|=\frac{1}{mn+1}\left(\genfrac{}{}{0pt}{}{mn+1}{n}\right)\end{array}$$(18)

On the other hand, we claim that

$$$ \begin{array}{c}\left|{\mathrm{\Sigma }}_{n+1}\right|=\sum _{k_1+...+k_m=n} \left|{\mathrm{\Sigma }}_{k_1}\right|\left|{\mathrm{\Sigma }}_{k_2}\right|\dots \left|{\mathrm{\Sigma }}_{k_m}\right|\end{array}$$$(19)

where  $$ k_1,\dots ,k_m$$  range over non-negative integers.

Suppose that  $$ \mathrm{\sigma }=⟨x_0,\dots ,x_{m\left(n+1\right)}⟩\in {\mathrm{\Sigma }}_{n+1}$$ . Clearly  $$ x_{m\left(n+1\right)}=1-m$$ . If  $$ s_k=x_0+\dots +x_k$$ , let  $$ n_j$$  be the maximal number less than  $$ m\left(n+1\right)$$  such that  $$ s_{n_j}=j$$  for  $$ j=1,\dots ,m$$ . It’s not hard to check that  $$ n_m=m\left(n+1\right)-1$$ , and that each of the sequences

$$$ \begin{array}{c}⟨x_0,\dots ,x_{n_1}⟩,⟨x_{n_1+1},\dots ,x_{n_2}⟩,\dots ,⟨x_{n_{m-1}+1},\dots ,x_{n_m}⟩\end{array}$$$(20)

belongs to some  $$ {\mathrm{\Sigma }}_k$$ . This means that there are natural numbers  $$ k_1,\dots ,k_m$$  such that  $$ n_0=m{k}_1$$ , and  $$ n_j-n_{j-1}=m{k}_j+1$$  for  $$ j=2,\dots ,m$$ , and evidently

$$$ \begin{array}{c}m\left(n+1\right)-1=n_m=m{k}_1+{\sum }_{j=2}^m\left(m{k}_j+1\right)=m\left(1+{\sum }_{j=1}^m{k}_j\right)-1,\end{array}$$$(21)

so  $$ {\sum }_{j=1}^m{k}_j=n$$ .

Conversely, if  $$ {\sum }_{j=1}^m{k}_j=n$$ , where each  $$ k_j\in N$$ , and  $$ {\mathrm{\sigma }}_j\in {\mathrm{\Sigma }}_{k_j}$$  for  $$ j=1,\dots ,m$$ , then the sequence obtained by appending  $$ 1-m$$  to  $$ {\mathrm{\sigma }}_1{\mathrm{\sigma }}_2\dots {\mathrm{\sigma }}_m$$  is in  $$ {\mathrm{\Sigma }}_{n+1}$$ . The correspondence is bijective, so the equation 3.4 is established.

Now the equation 3.2 and equation 3.4 are the same recurrence relation, and  $$ \left|{\mathrm{\Sigma }}_0\right|=1$$ , since the only member of  $$ {\mathrm{\Sigma }}_0$$  is  $$ ⟨1⟩$$ , so if we set  $$ C_0^{\left(m\right)}=1$$ , then it follows immediately that

$$$ \begin{array}{c}{C}_n^{\left(m\right)}=\left|{\mathrm{\Sigma }}_n\right|=\frac{1}{mn+1}\left(\genfrac{}{}{0pt}{}{mn+1}{n}\right)=\frac{1}{\left(m-1\right)n+1}\left(\genfrac{}{}{0pt}{}{mn}{n}\right)\end{array}$$$(22)

which are exactly the fuss-catalan numbers.

3.2. Bijections between counting problems

Like the original catalan numbers, fuss-catalan number can discribe a lot of combinatorics counting problems.

For example, like the generalized dyck path and m-ary trees, these two counting problems obviously get the same number,  $$ C_n^{\left(s\right)}$$ . We will talk about another counting problem in the following subsection.

3.3. Division problem

Catalan numbers count the number of ways to divide an  $$ n$$ -gon into  $$ n-2$$  triangles using non-crossing diagonals. We try to count the number of ways to divide an  $$ \left(\left(m-1\right)n+2\right)$$  -gon into  $$ n$$   $$ \left(m+1\right)$$  -gon using non-crossing diagonals.

Lemma 3.2

Dividing  $$ \left(\left(m-1\right)n+2\right)$$  -gon into  $$ n$$   $$ \left(m+1\right)$$  -gon using non-crossing diagonals can have  $$ C_n^{\left(m\right)}$$  different ways.

proof

We may use the mathematical induction.

Let  $$ n = 1$$ , we need to divide an  $$ \left(m+1\right)$$  -gon into an  $$ \left(m+1\right)$$  -gon. Obviously, there is only one way, because  $$ C_1^m=1$$ .

Assume the statement holds for some arbitrary  $$ k \ge 1$$ , that is:  $$ C_n^{\left(m\right)}$$  represents the ways that dividing an  $$ \left(\left(m-1\right)n+2\right)$$  -gon into  $$ n$$   $$ \left(m+1\right)$$  -gon.

We will now prove that if the statement holds for  $$ n$$ , it must also hold for  $$ n+1$$ .

Consider a newly-added vertex  $$ A$$  of the polygon, diagonals that consist of  $$ A$$  and other vertexes divide the polygon into two parts: an  $$ \left(m+1\right)-gon$$  and an  $$ \left(\left(m-1\right)n+2\right)$$  -gon.

The  $$ \left(\left(m-1\right)n+2\right)$$  -gon need to be divided into  $$ n$$   $$ \left(m+1\right)$$  -gon, which has  $$ C_n^{\left(m\right)}$$  different ways.

 $$ A$$  has  $$ \frac{mn+1}{mn-n+1}$$  choices in order not to have crossing diagonals. As for each newly-added vertex, the extra sizes have  $$ mn+k$$  choices, but when divided into n parts, repeated ways should not be considered. There are overall  $$ m-1$$  extra vertexes, which needs to be counted.

It's worth mentioning that internal edge changes from  $$ \left(m-1\right)n+1$$  to  $$ \left(m-1\right)\left(n+1\right)+1$$ , so a coefficient is needed.

Then we will prove the recursion relationship

$$ \begin{array}{c}\begin{array}{c}\frac{\left(m-1\right)n+1}{\left(m-1\right)\left(n+1\right)+1}\times m\prod _{i=1}^{m-1} \frac{mn+i}{mn-n+i}\times C_n^{\left(m\right)}\\ =\frac{\left(m-1\right)n+1}{\left(m-1\right)\left(n+1\right)+1}\times m\prod _{i=1}^{m-1} \frac{mn+i}{mn-n+i}\times \frac{1}{\left(m-1\right)n+1}\left(\genfrac{}{}{0pt}{}{mn}{n}\right)\\ =\frac{1}{\left(m-1\right)\left(n+1\right)+1}\times m\prod _{i=1}^{m-1} \frac{mn+i}{mn-n+i}\times \frac{\left(mn\right)!}{n!\left(\left(m-1\right)n\right)!}\\ =\frac{1}{\left(m-1\right)\left(n+1\right)+1}\times \frac{\left(mn+m\right)\left(mn+m-1\right)\dots \left(mn+1\right)}{\left(n+1\right)\left(mn-n+m-1\right)\dots \left(mn-n+1\right)}\times \frac{\left(mn\right)!}{n!\left(\left(m-1\right)n\right)!}\\ =\frac{1}{\left(m-1\right)\left(n+1\right)+1}\times \frac{\left(m\left(n+1\right)\right)!}{\left(n+1\right)!\left(\left(m-1\right)\left(n+1\right)\right)!}\\ =\frac{1}{\left(m-1\right)\left(n+1\right)+1}\times \left(\genfrac{}{}{0pt}{}{m\left(n+1\right)}{\left(n+1\right)}\right)\\ =C_{n+1}^{\left(m\right)}\end{array}\end{array}$$(23)

By the principle of mathematical induction, we have shown that the statement holds for all  $$ n \ge 1$$ .

Therefore, the lemma is proved.

From another perspective, the division problem is also the Fuss-Catalan number:  $$ C_n^{\left(m\right)}$$ .

To divide an  $$ \left(m\left(n-1\right)+2\right)$$  -gon into  $$ n$$   $$ \left(m+1\right)$$  -gon, we can choose one side, and find the first  $$ \left(m+1\right)$$  -gons that contain this side. Then the  $$ \left(m+1\right)$$  -gon will divide the original polygon into  $$ m$$  smaller regions, with each region corresponding to an  $$ \left(\left(m-1\right)n_i+2\right)$$  -gon, which satisfies:

$$ \begin{array}{c}{n}_1+n_2+\dots +n_m=n-1\end{array}$$(24)

Since one  $$ \left(m+1\right)$$  -gon has been used, there are only  $$ n-1$$  left.

We may denote the  $$ C_n^{\left(m\right)}$$  as the number of ways that divide an  $$ \left(m\left(n-1\right)+2\right)-$$  gon into  $$ n$$   $$ \left(m+1\right)$$  -gon. Then it’s clear that

$$$ \begin{array}{c}{C}_{n+1}^{\left(m\right)}={\sum }_{n_1+\dots +n_m=n}{C}_{n_1}^{\left(m\right)}{C}_{n_2}^{\left(m\right)}\dots C_{n_m}^{\left(m\right)},\end{array}$$$(25)

while the  $$ n_1,\dots ,n_m$$  are the regions that need to be further divided.

Acknowledgments

Ziqiao Xu, Zhanbo Liu, and Ziqian Wang contributed equally to this work and should be considered co-first authors. Also, we are sincerely grateful to Professor Dan Ciubotaru and NEOSHCOOL's teachers.