1. Introduction

The Report of the Ministry of Industry and Information Technology of the People’s Republic of China shows that due to the high value and influence of industrial data [1], the number of attacks to industry networks in 2020 increases more than 3 times than that in 2019, with the main break-point of Industrial Internet of Things (IIoT) devices because of low-defense. Because of this situation, encryption is a way to protect data. Although traditional cryptography could reach a perfect secrecy through the one-time-padding symmetric-key algorithm, the problem of its key distribution prevents the wide deployment in use. To solve this, quantum key distribution (QKD) is raised to share keys based on quantum mechanics [2].

The secrecy of QKD is based on the properties of quantum: no-cloning, collapse after measurement, and uncertainty [2]. With those properties, what the receiver receives is indeed what the sender sends, with any middle eavesdropping easy to be aware of. However, there are many challenges to deploying QKD systems into industrial networks. Compared with the high cost of constructing new fibers for QKD only, reusing the existing fibers by multiplexing the quantum channel with classical information channels through the wavelength division multiplex (WDM) technology is a more realistic method. Unfortunately, because the power of quantum signals is much lower than classical signals’, those classical signals produce strong noises, performing as spontaneous Raman scattering (SpRS), to quantum channels. What’s more, because of the low power of quantum signals, they are much harder to be detected after a transmission loss in fibers. All of those lead to a decrease of QKD performance, giving a secure key rate [3]. This paper is aimed to explore the environment of the QKD system where the influence of noises is lower.

To work out the low-noise schemes of WDM discrete variable QKD systems, this paper proposes an IIoT network architecture based on QKD systems and explores the influence caused by SpRS noises in theory. Then it constructs the model to illustrate how the system performance is influenced by SpRS noise and simulates those influences numerically. Finally, based on the comparison and discussion results, it concludes those low-noise schemes.

2. Related works

Many researchers have explored the feasibility of multiplexing quantum channels with classical channels. Kawahara et al. used 20% degradation of DPS-QKD system key rate as the criterion and showed the upper-bound noise of forward and backward SpRS with different detectors in carriers of 1536 nm (classical channel) and 1626 nm (quantum channel) separately through simulation [4]. Similarly, Zavitsanos et al. indicated that channel separation is essential and the accumulated Raman scattering photons are the dominant noise source through experiment [5], showing that an essential influence appears when the noise is greater than -10 dBm per channel in 3 km fibers.

Both of the above have shown the main noises and the way that those noises influence the QKD system’s performance, but lack a combination of real industrial channels. In this paper, those results would be combined with real industrial environments to work out the QKD system performance through simulation.

3. Simulation methods

3.1. Network architecture

This paper proposes an IIoT network architecture based on quantum mechanics security shown in Figure 1. In this architecture, industrial data signals and quantum signals are transmitted in one single fiber based on WDM, where the transmission direction of quantum signals is the same as forward industrial data signals’, but opposite to the backward’s. This system architecture could provide a highly reliable and secure solution which meets the requirement of both encrypted data transmission and secure keys distribution.

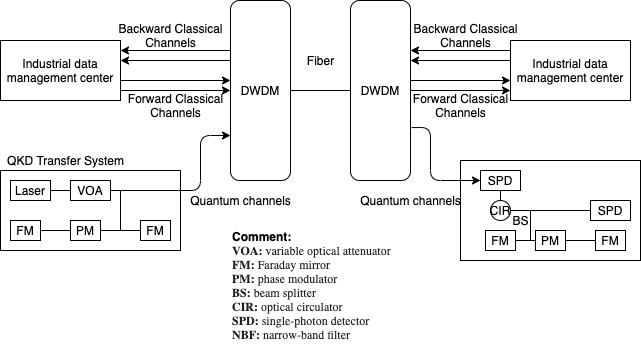
Figure 1. IIoT Network Architecture with QKD Systems.

3.2. SpRS

Data are normally transmitted uni-direction or bi-direction in an industrial network. As a result, quantum channels may face noises as forward SpRS, backward SpRS, or bidirectional SpRS from classical channels in different situations. Suppose a light pumper \( p \) at point 0 generates lights with pumping power \( {P_{p}}(z) \) , the pump power at point \( z \) is [4]:

\( {P_{p}}(z) ={P_{p}}(0) exp[-{α_{p}}z] \) (1)

where \( {α_{p}} \) is the loss coefficient of the pump light. Let \( {d_{z}} \) be the distance of point \( z \) and 0 and η be the Raman efficiency, the SpRS generating power ( \( dP(z) \) ) at point \( z \) is [4]:

\( dP(z) =η{P_{p}}(0) exp[-{α_{p}}z]{d_{z}} \) (2)

Let \( L \) be the destination point and \( {α_{r}} \) be the fiber loss coefficient for SpRS lights, the total forward scattering power over the whole fiber length is [4]:

\( P_{raman}^{f}=\int _{0}^{L}η{P_{p}}(0) exp[-{α_{p}}z]*exp[-{α_{r}}(L-z)]{d_{z}} \)

\( P_{raman}^{f}=\frac{η{P_{p}}(0)}{{α_{r}}-{α_{p}}}\lbrace exp[-{α_{p}}L]-exp[-{α_{r}}L]\rbrace \) (3)

If \( {α_{r}}≈{α_{p}} \) , Eq. (3) is rewritten as [4]:

\( P_{raman}^{f}≈η{P_{p}}(0)exp[-{α_{p}}L]L \) (4)

Similar to the forward scattering, the total power of backward scattering is [4]:

\( P_{raman}^{b}≈\frac{η{P_{p}}(0)}{2{α_{p}}}\lbrace 1-exp[-2{α_{p}}L]\rbrace \) (5)

3.3. Performance Evaluation of QKD

3.3.1. Secure key rate. The GLLP formula [6] assumes that for imperfect pumpers which may produce multiple photons signals, only the single-photon signals could be used to generate secure keys. Based on its assumption and results, the secure key rate \( S \) of a BB84 protocol system is computed as [2,7]:

\( S≥{Q_{μ}}\lbrace {H_{2}}({e_{μ}})+Ω[1-{H_{2}}({e_{1}})]\rbrace \) (6)

where \( {Q_{μ}} \) and \( {e_{μ}} \) are the gain of signal states and quantum bit error rate (QBER) for \( μ \) photons. \( Ω={Q_{1}}/{Q_{μ}} \) and \( {H_{2}}(x)=-x{log_{2}}{(x)}-(1-x) \) . Let \( {η_{n}} \) be the detector which detects the signal if an n-state photon is sent, the probability that the receiver could detect the signal if the sender sends \( n \) photon states indeed \( {Y_{n}} \) is expressed as [7]:

\( {Y_{n}}={Y_{0}}+{η_{n}} \) (7)

where \( {Y_{0}} \) is the background noise assumed independent with signal states. This paper only considers that the background noise only contains SpRS noises ( \( P_{raman}^{f} \) and \( P_{raman}^{b} \) ) and dark count noise. The loss coefficient of an \( l \) length fiber is \( α \) dB and the detection efficiency of the detector is \( {η_{D}} \) , then \( {Y_{0}} \) and \( {η_{n}} \) are written as [7]:

\( {Y_{0}}=2{p_{dark}}+P_{raman}^{f}+P_{raman}^{b} \)

\( {η_{n}}=1-{(1-{10^{α/10}}{η_{D}})^{n}} \) (8)

Let \( {Q_{n}} \) (the detection expectation) be the production of the probability of sending \( n \) photon states and the probability of having a detection result based on whether photons sent, it is computed as [7]:

\( {Q_{n}}={Y_{n}}{P_{μ}}(n)={Y_{n}}\frac{{μ^{n}}}{n!}{e^{-μ}} \) (9)

3.3.2. Quantum bit error rate. The error bit on receiver’s side comes from the background noises and measurement errors. When the sender sends \( n \) photon states, the error bit \( {e_{n}} \) based on a measurement error probability \( {e_{det}} \) is computed as [7]:

\( {e_{n}}=\frac{{e_{0}}{Y_{0}}+{e_{det}}{η_{n}}}{{Y_{n}}} \) (10)

combined with Eq. (7) and Eq. (9), the total bit error rate is [7]:

\( {{E_{μ}}Q_{μ}}=\sum _{n=0}^{∞}{e_{n}}{Y_{n}}{P_{μ}}(n)={e_{0}}{Y_{0}}+{e_{det}}(1-{e^{-ημ}}) \) (11)

4. Result and discussion

4.1. Result and analysis

This paper demonstrates the secure key rate and quantum bit error rate depending on the variety of transmission distance, power of classical signals, and channel location. All simulated channels are around the C-band where the attenuation of fibers is the lowest. For initialized settings, 97 channels are initialized from 192.40 THz to 197.20 THz (0.05 THz for each channel spacing) and are numbered from 1 to 97. Then, to consider the worst situation, the length of the transmission is set to 25 km where the forward SpRS produces the highest noise (shown in Figure 2) with the pumping power of 10−5 W according to the normal requirements of industrial usage [8]. Finally, only the secure key rate above 0 is considered as a negative key rate is meaningless.

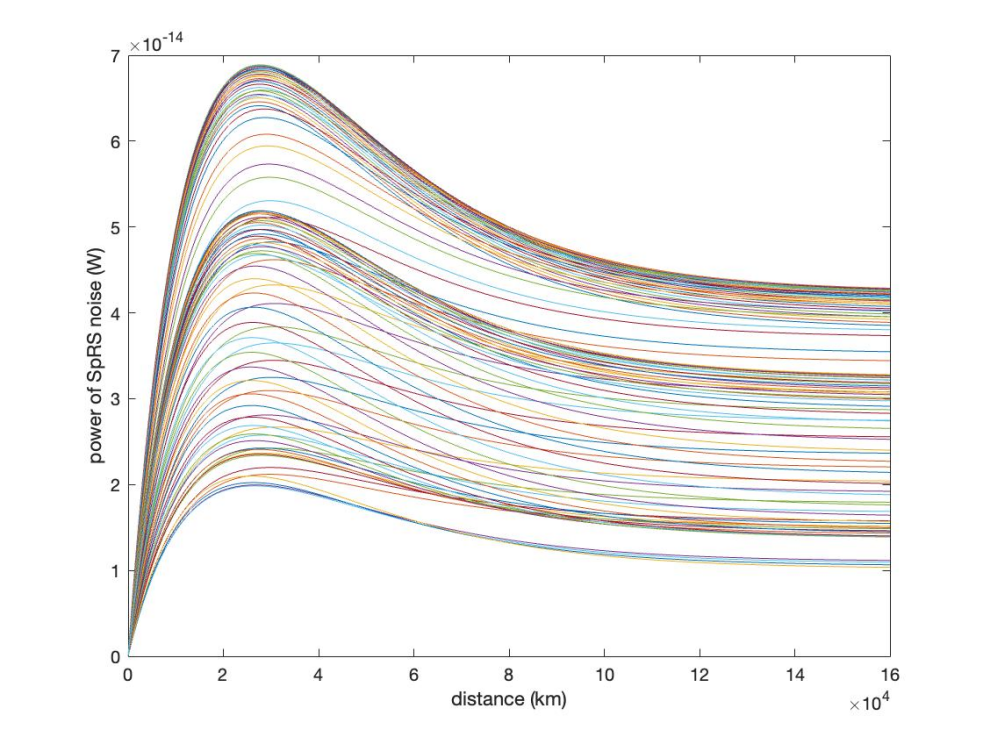
Figure 2. Power of SpRS Noise Varying with Distance (Each line represents a single channel)

To simulate a real fiber situation with multicommunications, totally 16 channels are set at the same time (4 forward and 4 backward for classical channels, 8 forward for quantum ones). 4 forward channels and 4 backward channels are set from 194.50 THz (45) to 194.90 THz (51) and from 195.00 THz (53) to 195.30 THz (59) separately with a spacing of 0.1 THz for each channel. In this situation, Raman efficiency for all 97 channels is computed and illustrated in Figure 3.

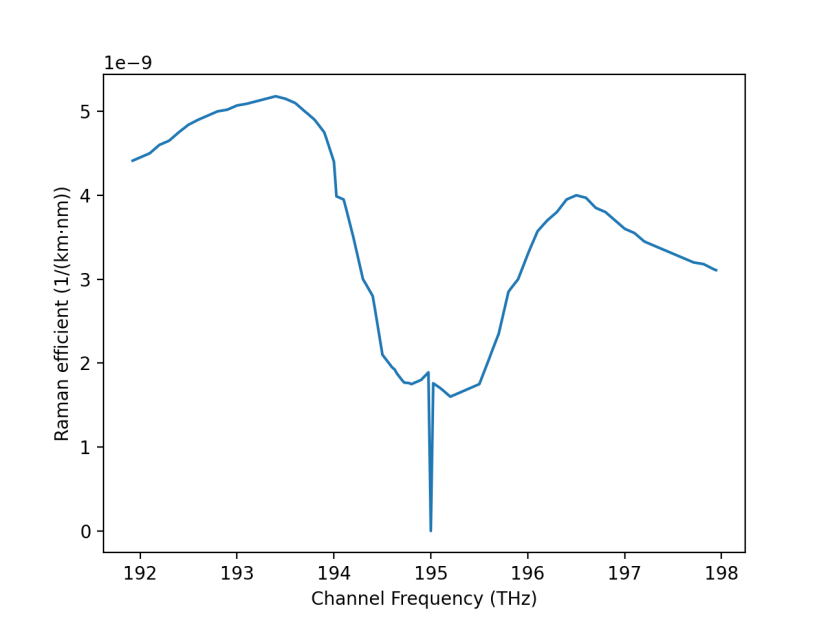
Figure 3. Raman efficient/channel.

Firstly, this paper explores the SpRS influence with the transmission distance. 8 quantum channels are set between 29-41 with pumping power of \( {10^{-5}} \) W for all classical signals. The distance varies from 0 to 160 km and the secure key rate and quantum error bit rate for none of the classical channels activated, forward channels activated only, backward channels activated only, and all classical channels activated are illustrated in Figure 4.

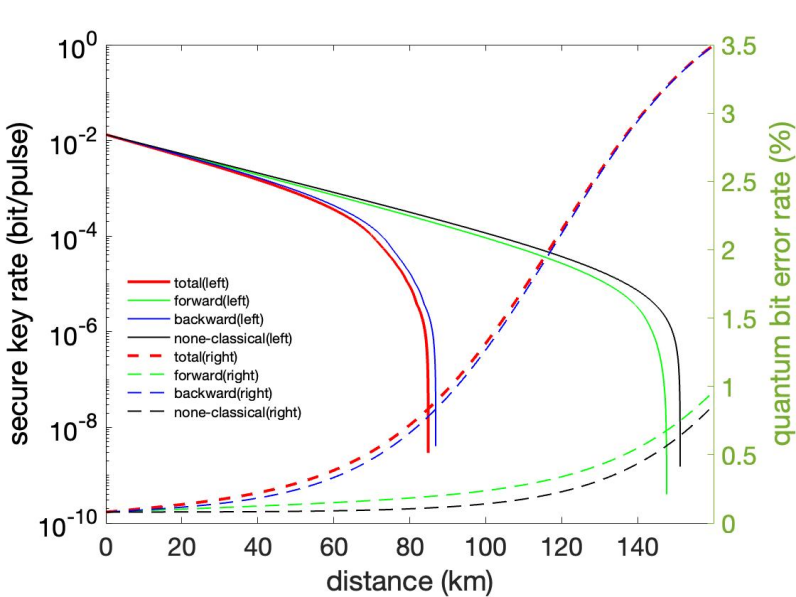
Figure 4. Key Rate/Error Rate Varying with Distance.

From Figure 4, it is obvious that quantum error bit rate increases with the increasing of transmission distance, and the secure key rate decreases with the heavier and heavier SpRS noise. The lowest acceptable secure key generating rate for a QKD system should be no less than \( {10^{-8}} \) bit/pulse [9]. Due to this limitation, the QKD system with a bidirectional communication fiber works well within around 85 km, while the key rate is higher than 0.00375 bit/pulse in 25 km and drops quickly after 68 km. What’s more, this figure also tells that the main noise is caused by the backward channels, and the bidirectional SpRS noise reduces the performance to around only 57% of its original (without any classical channels).

Next, SpRS influence with the strength of classical signal power is simulated. In this simulation, channels are set at the same position as before distance simulation. The transmission distance is fixed to 25 km. Then Figure 5 represents the secure key rate and quantum bit error rate with classical signal power varying from \( {10^{-7}} \) W to \( {5*10^{-4}} \) W.

Figure 5. Key Rate/Error Rate Varying with Classical Signal Power.

From Figure 5, power of classical signals less than \( {1.27*10^{-4}} \) W of bidirectional classical channels could be tolerant in this QKD system, where the key rate is 0.00356 bit/pulse when the power is \( {10^{-5}} \) W and fails dramatically when the power is greater than \( {10^{-5}} \) W. Same as before, the SpRS of backward channels is much larger than that of forward channels.

Finally, SpRS influence with different positions of classical channels is simulated by changing the quantum channels in the range of channel 1 to channel 97 with a spacing of 0.1 THz for each channel where all the 8 classical channels keep unchanged as before (45-51, 53-59). This time, the power of classical signals is fixed at \( {10^{-5}} \) W and the transmission distance is fixed at 25 km. The x-axis in Figure 6 is the start channel number for the following 3 channels (e.g. 1 represents channels numbered 1, 3, 5, 7).

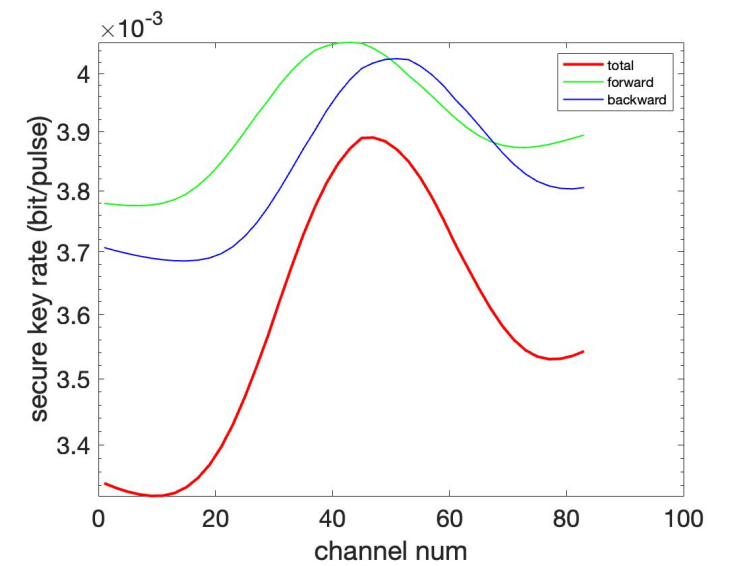
Figure 6. Key Rate Varying with Quantum Channel Position.

The reason for the secure key rate going down first, then increasing to the peak point, dropping down again, and finally increasing is shown in Figure 3 as the Raman efficiency for each channel is negatively correlated to the key rate. Figure 6 shows the closer quantum channels to classical channels and the higher performance of the QKD system it would have. Also, it is obvious that compared with the frequency of classical channels, quantum channels in higher frequency perform better than those in lower frequency.

The reason for all three curves’ peak points’ channels (the channel owing the highest key rate/facing the lowest noise influence) are not exactly the channel of 53 is that those channels are not single channels but a group of channels. For the group of forward channels, they range from 45-51, where the peak should be between this range, which is the same as backward channels.

4.2. Discussion

To conclude in the C-band frequency based on industrial environment settings with a situation of 4 forward, 4 backward classical channels and 8 forward quantum channels, suggestions of settings are listed as follows:

• Backward classical channels produce much more SpRS noise than forward ones normally. As a result, multiplex quantum signals with forward signals but avoid backward transmitting when quantum channels are activated as much as possible.

• The transmission distance within 85 km with classical signal power of \( {10^{-5}} \) W makes the use of advantages of QKD systems, while for a fixed distance of 25 km (where the SpRS noise is the maximum), classical signals could be generated within the power of \( {1.27*10^{-4}} \) W for each channel.

• For the choice of channels, classical channels and quantum channels should be as much closer as possible. Also quantum channels are suggested to be placed in higher-frequency channels rather than lower-frequency channels compared with classical channels’ frequency.

5. Conclusion

To meet the requirement of highly secure IIoT network data transmission, this paper designs an system architecture based on QKD systems, simulates the expecting performance of this system under the normal industrial network conditions and raises instructions of settings to deploy this system. Through the result based on the proposed system architecture, QKD system works well in IIoT network conditions and takes advantages of it in a situation of transmission distance less than 85 km and classical signals strength less than \( {1.27*10^{-4}} \) W of each channel generally. However, with different usage requirements, the number and kind (forward/backward) of classical channels used are different. As a result, companies could adjust their network architecture and settings based on figures in this paper and put quantum channels as much closer to classical channels with a higher frequency as they can to increase QKD system performance. Finally, to avoid a huge performance drop, it is suggested that transmission distance and pumping powers for one single pair of QKD transmitting/receiving devices should not be closed to their acceptable limitations.