1. Introduction

Digital signature is a kind of mathematics scheme that ensures the privacy of conversation and transaction, data integrity, message authenticity, and sender's non-repudiation. Blockchain is a new kind of computer technology, which integrates the storage of distributed data, the exchange of peer, the agreement mechanism, and the digital encryption. It's decentralized, secure, and open. Digital signature plays an important role in the blockchain. Generally speaking, the digital signature is composed of two algorithms: signature, and authentication. Signature uses a private key to deal with information and create a signature; Authentication is to use a public key to authenticate the message. In the case of Bitcoin, it is a string created by the sender of bitcoin to verify the identity of the signer and the timing of the signature, thus verifying the authenticity of the message. The development of digital signature not only promotes but also restricts the development of the blockchain.

First of all, the basic theory of digital signature and the process of signing are introduced. Then, the paper introduces the principles, advantages and disadvantages of the five categories: Aggregate, Loop, Blind, Group and Agent. Furthermore, the basic structure of block chain is introduced, and the key techniques are analyzed, including data level, execution level, contract level, network level, agreement level, and application level. It means that the digital signature runs through the entire blockchain.

Secondly, the author compares the above five kinds of digital signatures, and finds that their main ideas are different. For instance, the aggregation signature is based on the threshold, and the group signature is the discrete form of the elliptic curve. It also analyses their advantages and disadvantages, such as the traceability and anonymity of the group signature, and the flexibility of the proxy signature. At the same time, this paper analyses the research work in the five fields of digital signature, and analyses the existing problems, solutions and prospects.

This thesis is structured as follows. The second part gives a brief introduction to the fundamental concepts of Digital Signature and Blockchain. In the third part, it makes a comparative study on the five types of digital signatures, and make some analyses.

2. Basic knowledge

2.1. Digital signature

In the process of sending a message, the sender uses the hash function to generate the digest, then uses its key to encrypt the digest, and sends it to the recipient as a digital signature. As illustrated in Figure 1, the receiver first computes the digest from the original packet with the same hash function as the sender, and then decrypts it with the public key of the sender. If both abstracts are identical, then the recipient will be able to verify that the digital signature came from the sender.

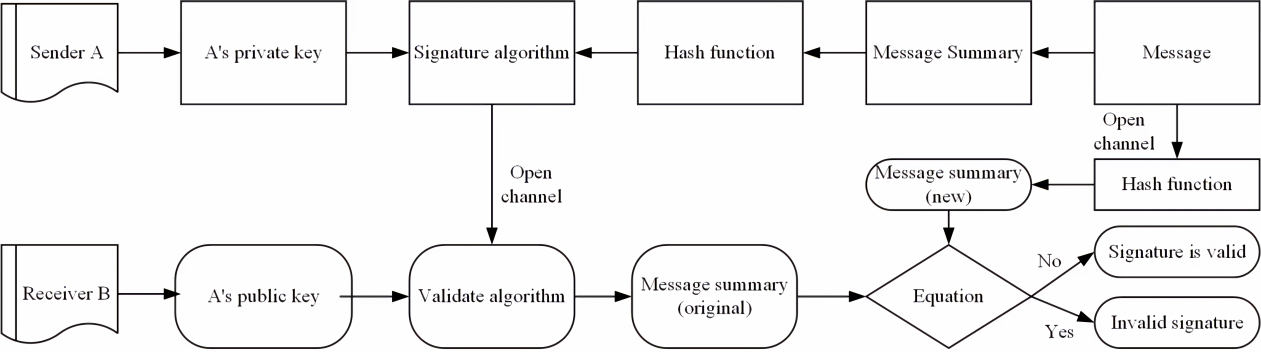
Figure 1. Digital signature processes [1].

Figure 2. Group signature process [4].

2.1.1. Aggregate signature [2][3]. A variant signature is used to aggregate multiple signatures into one signature. A collective signature can combine n signatures on n messages from n users into a short signature, and the resultant signature can assure the verifier that n users have actually signed n corresponding messages.

2.1.2. Group signature [4]. Group Signature enables a Band Member to act on behalf of a Band Member without disclosing Band Member status. Only a designated group administrator is able to identify the party member that issued the specified signature, as shown in Figure 2. Group Signature enables a team member to sign a message for the group. Signatures can be validated with one set of public key, but not the signers' identity. Moreover, it is impossible to determine if two signatures belong to the same family. However, an appointed group administrator who can publish his or her signature in case of dispute, that is to say, disclose the identity of the signatory.

2.1.3. Ring signature [5]. Initially proposed by Rivest et al., it is a simplified group signature with only ring members and no manager. This is a group signature with privacy problems as shown in Figure 3: A consumer can sign anonymous messages on behalf of a group of people, which means that it is currently subscribing to the messages. Each certificateur can be certain that one of its members has signed it, but does not know who it is.

Figure 3. Ring signature process [5].

2.1.4. Blind signature [6]. Blind signing is a method of obtaining a signature from a signer, which prevents the signing of the agreement view from the signing party and the resultant message signing pair. The Anonymous Digital Payment System uses a Blind Signing Scheme as illustrated in Figure 4.

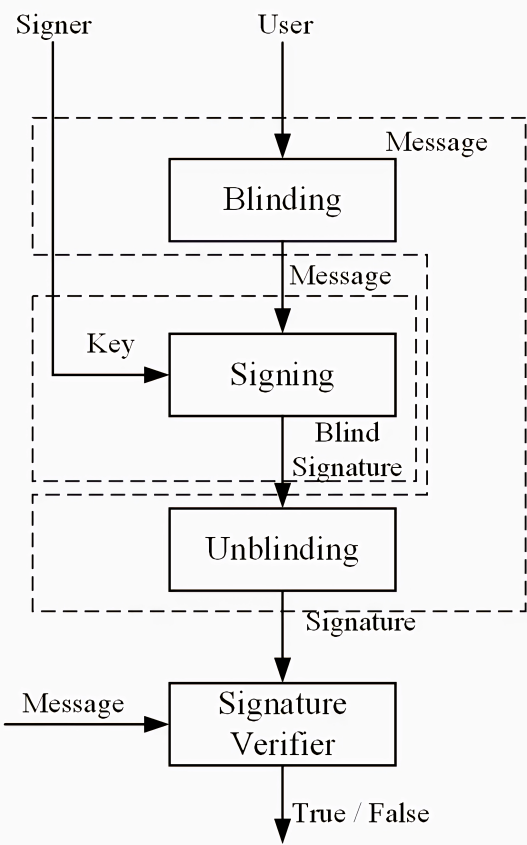
Figure 4. Blind signature process [7].

Figure 5. Proxy signature process [9].

2.1.5. Proxy signature [8]. The agent's signature enables an appointed individual, known as a proxy signatory, to represent the original signatory. In addition to the original signers, as shown in Fig. 5, the designated signatory can also make an efficient agent signature for the original signatory. But an undesignated third-party cannot create valid proxy signatures for agent signers. By means of a proxy signature, the authenticator can confirm whether the original signers agree with the signed message.

2.2. Blockchain

Strictly speaking, the Block Chain is a kind of serial data structure, which is composed of pieces of data in order of time, so that it cannot be modified or falsified.

Generally speaking, the blockchain technology is a type of computing and distribution infrastructure. Based on the block model, it can verify and save the data. Moreover, it can create and renew the data by means of a distributed node.

As illustrated in Figure 6, the blockchain system is composed of a data layer, network layer, consensus layer, incentive layer, contract layer, and application layer.

(1) The network layer consists of distributed network, data transfer mechanism and data authentication mechanism.

(2) The actuator level integrates economic factors into the blockchain.

(3) The data layer encapsulates the basic data block, the basic data and the algorithm, and so on.

(4) Application layer encapsulates a variety of application situations and cases of blockchain.

(5) Contract layer is mainly used to encapsulate various scripts, algorithms, and intelligent contracts, which is the foundation of the block's programmable characteristics;

(6) The consensus layer is used to encapsulate all kinds of agreement algorithms in the network.

Figure 6. The six layers of blockchain.

3. Comparison of digital signature schemes

This part compares five kinds of digital signatures and introduces their main ideas, as shown in table 1. For example, group signatures are discretized based on elliptic curves, while aggregate signatures are mainly based on threshold signatures. At the same time, it analyzes their advantages and disadvantages, as well as the work of scholars in the five fields of digital signature, and summarizes the existing problems, solutions, and prospects.

Table 1. Comparison of different digital signatures.

3.1. Aggregate signature

Kang Qiao et al. [10] presents a novel blockchain signature system to protect the privacy of block transactions. Compared with other methods, this method not only decreases the memory cost but also improves the communication efficiency and the calculation of signing and authenticating. The theory shows that this solution has high security and high efficiency, and it can ensure the security of the block trade. This paper presents several kinds of methods, for example, creating private key, creating public key and signing digital signature.

This paper proposes a novel and efficient general signing scheme for short-signed documents. In this solution, the overall signing length is constant regardless of the number of users, and thus it can decrease the storage cost. Furthermore, it uses discrete logarithms instead of bilinear mapping, which can decrease the computational cost. At the same time, the security of the receiver's identity can be ensured efficiently in a block chain transaction. The user may reduce the signing count from n to 1 when a transaction has n items and m outgoing addresses.

3.2. Group signature

Jan Camenisch et al. [4] figured implementations of group signature schemes have the undesired property that the length of the public key is linear in the size of the group. Unfortunately, they have the following disadvantages: -Group Public Key Length or Signature Size Dependent on Group Size. This is a big problem for a big group. -Add a new member of the group; the user must at least change the public key. In order to do so, they use new independent techniques such as the efficient proof (or signature) of the double discrete log, the E root of the discrete logarithm, and the E root. Of particular interest is the proof of signature knowledge. The Probability Interactive Protocol between Appointed Group Administrator and Group Member. It consists of a group's public key y, a group member's private key, and a group administrator's confidential management key. Sign Probability Algorithm, which returns the signature s of M when a message is entered and the key of a group member. Authentication: The method that returns the signature when the information m, the signature s, and the public key of the group is Y. Open: When the signature s is entered and the secret management key is input to the group manager, the algorithm returns the identity and the evidence of the group member that created the signature s. Assume that everyone in the group is in a safe relationship with the management of the group. The Group Signature Scheme shall meet the following properties: Only members of this group can sign the messages properly (no password) properly. 2. Unable to determine which of the group members (anonymously) signed the report or whether it was published by a single member of the group (disjoining). 3. Other group members may not be able to avoid signing or signing; this is not true for the group manager (Frame Attack Protection) This paper uses a "model system" where one side is trying to convince the other that they are aware of a given amount of data without giving them anything useful.

3.3. Ring signature

Sherman S.M. [5] proposed a novel approach to construct an ID-based ring signature which requires only two matching calculations per set. Furthermore, it has been shown that this method is very robust to the random selection of information and identity attacks, and can be applied to many other ring signature schemes. Furthermore, they are being extended with a view to encouraging a common approach.

Using the bifurcation theorem, it has been shown that this approach is not only robust to self-adaptation but also to identity attacks, as shown in Table 2. Expensive measures have been considered, e.g. point addition at G1 (G1 Add), point multiplication at G1 (G1 Mul), multiplication at G2 or Zq (G2/Zq Mul), Hash to Group (Hash), and pairing (pairing). Their BLS short signature relies on map-to-point hashes. Table 2 summarises the efficiency of the proposal. Considering the total cost of creation and verification of signature, it is proved that this approach has the only identical matching ratio, and the total number of other operations is the lowest. Furthermore, this approach can also be used to compute non-participants simultaneously, which is impossible with other solutions. Considering the size of the signature, it is as complex as the others, and does not have to spend too much time on the signature. Finally, all the proposed algorithms have been proven to be secure and bifurcated in their proof.

Table 2. Comparing Bilinear Pairings and ID-based ring signature [5].

Rebekah Mercer et al. [11] found that anonymity cannot be achieved with normal ring signatures. They use a unique ring signature scheme that works with existing blockchain systems. Their implementation of the Unique Loop Signature (URS) is based on secp256k1, which is the first such architecture to be able to be easily implemented as an Ethereum Intelligent Contract. The Franklin-Zhang URS architecture was used to generate a noninteractive zero knowledge proof (NIZK) solution, which significantly increased the effectiveness of previous interaction solutions. The present research examines the existing solutions that are not intrinsic to the individual privacy of the current blockchain system. Studies have found that certain solutions offer anonymous access to the block chain, while other solutions offer what it describes as "specious". Both have possible limitations - for truly anonymous blockchain systems, once transparent transaction ledgers have "opaque" and require additional trust to build such schemes. At present, there is no solution or system that is able to keep some level of transparency on the Block Chain Platform and keep real anonymity for each user.

3.4. Blind signature

Qing Chun Shen Tu et al. [12] discovered that coin blending providers (mixers) were aware of every user's output address, so that they could not provide real anonymity. They propose a centralized coin mixing algorithm based on an elliptic curve blind signature scheme (called blind mixing) that prevents the mixer from linking the input address to the output address. A comparative study shall be carried out between three blind signature schemes: blind, blind and RSA Coin-Mixing.

The comparison of blind, blind and RSA Coin -mixture algorithms is given in table 3. Based on public-key cryptography, Blind Mixture adopts short-key-length ECC, Blind Coin adopts Bilinear Combination, and RSA Combination RSA is inefficient.

The Blind Mixture User has a unique Access Address, so user cannot locate the Store Address or Withdraw Address of the other User. The RSA Coin Combination also has a unique memory location, which makes it easy for an attacker to obtain all of the incoming and outgoing addresses.

Blind Currency Deposit Certificates require a signature and a unique storage address, while Blind Currency requires only a storage address; but in RSA Coin Mix, it is possible to falsely claim Bitcoin. Because it is very simple to obtain the ID through the bank's public address, the proactive attacker may be able to make a blind signing request in advance.

Table 3. Comparisons between Blind-Mixing, Blind-Coin, and RSA Coin-Mixing algorithms [12].

They proposed a centralized coin-mixing algorithm named Blind-Mixing, which is based on the ECC Blind Signature, to avoid the problem that the mixers could not obtain the IP address of the user. Thus, it is possible to improve the anonymity of the mixture in the center. Based on the analysis, Blind Mixing is able to resist even a super attacker. Furthermore, it is possible to remove anonymity with high likelihood of success because it is based on a common protocol. Additionally, RSA Coin-Mixing allows a person's bitcoins to be fraudulently claimed by another person so that they can easily earn or leave. This paper show that the proposed method is more effective than blind or RSA Coin-Mixing.

Qianhong Wu et al. [13] looked into the possibility of jointly managing bitcoin transactions in which multiple participants are in possession of bitcoin and making it possible for multiple participants to keep their anonymity. Consider a case where a merchant has a Bitcoin account, but permits multiple people to manage it jointly. For example, an enterprise may entrust one or more of its departments with managing its own accounts. Then consider a case where several peers, for example, a research group, have their own individual portion of their accounts. The main problem is that there is a lack of certainty among those who sign the contract in each field. To solve the problem, it proposes an uncertain partially blind threshold signature and expand it.

First of all, it has been demonstrated that the system is secure from counterfeiting. The attacker might try to forge a valid signature (or a transformation script for a successfully executed transaction) without a valid key, whereas others would have to authenticate it with a public key. Furthermore, the attacker is unable to link the signature to the blank message. So if an attacker doesn't have Hi's Secret Key, he won't be able to find out anything about it. Also, because fake stocks can't be reset to 0, it's important for at least t fair participants to have a secret. Therefore, if an attacker has less than t honest participants, it is not possible to create a valid transaction log to deceive the system. Then, it analyses the safety of Bitcoins' management. The Preferred Participant must ensure that the Transaction is completed successfully. Because there is no way to delete the base multi-signing scheme without the agreement of the two sides, the resultant signature will not be validated and thus void the transaction. It then calls upon all sides to reach an agreement with the platform. Basic Shamir Security Sharing.

If the deal is below the threshold, or if the trading is not authorized by the platform, then the nonblind signing is invalid, and the deal fails. Furthermore, it is not possible to falsify the basic threshold ECDSA signature (Chow, 2005), nor is it possible to extract a participant's key (Vo, 2003). Thus, if r privileged participants, t 1 normal participant, and the platform are not able to create a low level ECDSA multiple signature, then a Bitcoin transaction will be identified successfully.

In summary, the joint control of Bitcoin transactions was examined. This platform enables the participant to pre-negotiate the public message with the receiver, and then use their own secret keys to realize the blind/anonymous trade. The proposed scheme is compatible with current Bitcoin systems. The results indicate that this plan is safety and reliability, and it has some application value.

3.5. Proxy signature

Seungjoo Kim et al. [9] Two new types of digital proxy signatures were proposed for the first time, namely, partial authorization with authorization and threshold authorization. In threshold authorization, partially authorized proxy signing shares the signature authority of agent signer on message. Partial authorization with authorization combines the benefits of partial authorization with the benefits of authorization. Therefore, this delegation process is fast and suitable for restrictive documents to be signed. In addition, since some authorized agents can specify their validity period, this scheme does not require additional agency revocation agreements.

Nowadays, in a group-oriented society, it is usually desirable to share the signature rights of a proxy signer on a message. For instance, employee Alice has instructed her secretary, Bob, to answer on her behalf. But let's assume that Secretary Bob is not acting on Alice's prearranged orders. He doesn't sign papers demanding immediate answers, and he doesn't sign documents that Alice asks him to keep. As a result, for security reasons, the company's policy might be to have k proxy signers sign documents rather than one.

Two new kinds of proxy signature are presented in this paper. The first is partial authorization with authorization. Proxy signature is better in calculation and structure than authorized proxy signature.

The other is a proxy signature with threshold authorization. In a future where there is a high concentration of collective action, it is advisable to entrust the signing authority of this information to a team consisting of N agent signers. This article presents a partial authorization of agent signing scheme and an agent signing scheme with (t, n) threshold that do not expose agent shares.

Byoungcheon Lee. [8] have shown different attack scenarios for existing proxy signature schemes, which suggests that a very careful design of proxy signature schemes is required. Based on the weak point, they provide a new kind of proxy signature: strong agent signature and weak agent signature, appointed agent signature and unappointed agent signature, and self-proxy signature. This paper proposed a simple, efficient, and non-designated proxy signature scheme for multi-delegate multi-agent signatures.

Since no agent signature is required during the issuance of agent keys, this method has higher flexibility and efficiency in a lot of actual use. It can be applied to multi-proxy signatures where multiple original signers delegate their signature capabilities to unspecified proxy signers. There are a lot of departments in a company, for example, Human Resources, Finance, Business, and General Affairs. The employee would like to get a signature on some of the typical data from those departments. If this is a typical message, these departments can delegate their signature functions to the staff with explicit authority. If an employee's message is in compliance with an authorization order, the employee can create more than one proxy signature on his own.

Alternatively, the employee would like to have the proposal signed by the department manager, supervisor, and president. He had gone over his proposal several times with them, and his final proposal had only a few minor changes. If more than one of his bosses gives him their signature capabilities through a more formal model, he can create multiple proxy signatures on his own without any further communication with them. In practice, it is quite common to have multiple delegations without specifying a proxy signer.

A proxy signature is a useful tool when one of the parties has to delegate their signature functions to the other. But in the distributed environment, it is hard to guarantee the reliability of the original signers, the proxy signers, and the proxy key distribution protocols. There is a risk in passing the signature function to someone else. Therefore, when designing a proxy signature scheme, it is important to make clear the responsibilities of proxy signers, and to avoid any possible misuse.

4. Conclusion

This paper gives an overview of blockchain, introduces the classification and characteristics of different digital signatures, and analyzes and summarizes the work of scholars in the field of digital signatures. Through the summary of this article, readers can have a clear understanding of various digital signatures. The results show that the aggregate signature can decrease the memory space and the net flow rate, particularly when the signing rate is small but the rate of verification is high. But it's more complicated than a typical signature, which adds to the cost. Proxy signatures are simpler but less secure than aggregate signatures, so it is necessary to reasonably select different digital signatures in different scenarios.

Based on the above overview of blockchain and digital signatures, the paper offers suggestions for improving security in related areas in the future. Firstly, when the signer uses the group signature, the anonymity of group signatures should be given full play to improve its security value. Secondly, in the process of digital signature, the signer should try to combine the digital signature and timestamp to optimize the digital signature algorithm.