1. Introduction

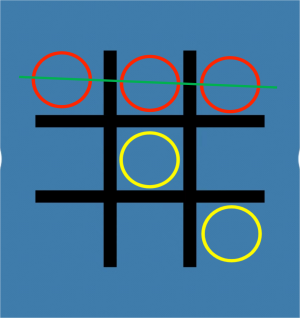
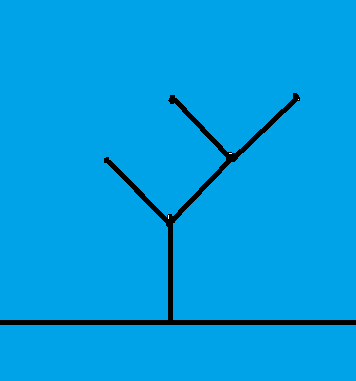
In recent times, due to the rapid development of Artificial Intelligence (AI)-based algorithms, AI in games has become an interesting topic for research in both academia and the game industry [1]. In this paper, the combinatorial game is studied. Participants of the combinatorial game can be divided into two sides and they can take turns to act. Two players can see the whole situation when making decisions and all actions will translate the current situation into the next situation with certainty. After the game starts, it will be finished in a limited number of steps. The normal tic-tac-toe game is for two players taking turns to draw “X” or “O” individually on a paper with a 3 plus 3 square grid and the one whose drawing forms a line like a row, a column, or an oblique line will lose the game, as shown in Figure 1 [2]. In addition, the green hackenbush game is still for two players to play and they are called the left and the right. They take turns removing different colored edges on a picture. Any edges that do not connect with the ground should be removed together. In the end, the one who moves the last edge will win the game, as seen in Figure 2 [3].

The normal version of the combinatorial game already has very detailed solutions and algorithms. However, based on the normal version, many varieties of combinatorial games can be explored. This paper concludes the strategy of two combinatorial games, namely the green hackenbush and tic-tac-toe game. The strategy will be helpful for readers to have a broader understanding of these two games’ strategies and come up with more advanced strategies.

2. Reverse misère version in tic-tac-toe

2.1. Introduction about the rule

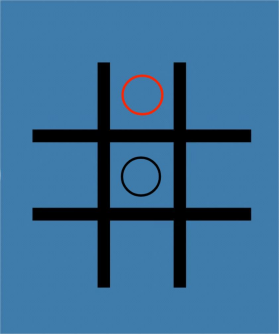
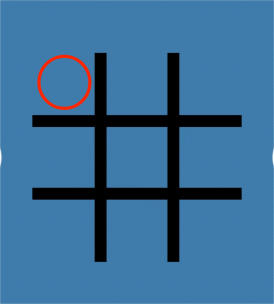
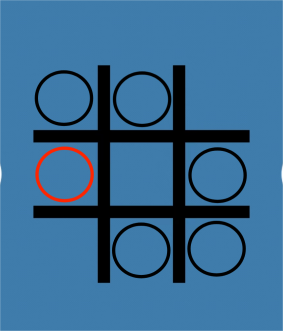
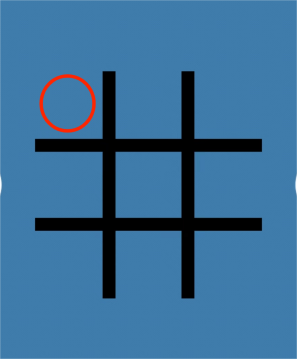
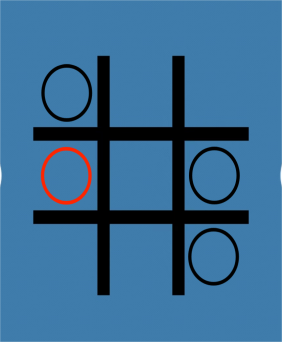
The rule for this new game is that both players use the “X” or “O” and put it in the compartments. Both of them can see the differences in the picture. When one player causes a line with all the previous “X” or “O”, that player will lose the game. This is a very simple case of the losing result for the first player because the red “O” causes a line by his or her last step in Figure 3. The first player puts “O” in the compartment (2,2). Then the second player puts it in the compartment (1,1). And it turns to the first player again. The first player puts it in the compartment (3,3). As a result, a line is formed in the picture, and the first player will lose [4].

Figure 3. The red “O” loses in the reverse misère version.

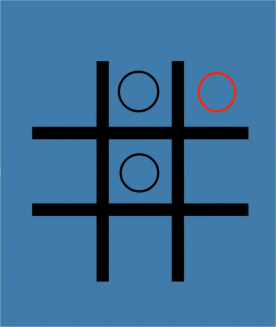
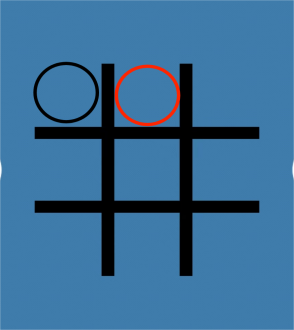
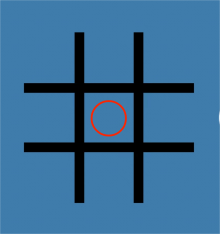
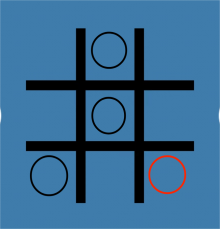
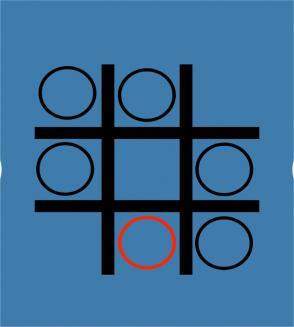
Firstly, as shown in Figure 4, the first player puts “O” in the central compartment (2,2). Then the second player puts it in the edge or the corner compartment (1,2). The first player draws the next step in compartment (1,3) and the second player draws in the compartment (2,3). It is not hard to find that after four times, the first player will lose. Obviously, no matter where he puts it, the “O” will connect a line, since all the lines (oblique lines and straight lines) have been occupied by two. This is called a P-position.

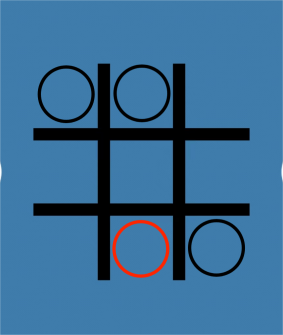
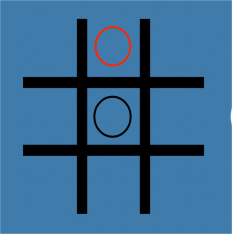
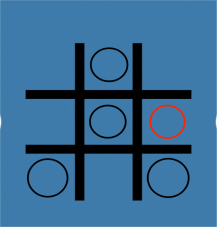
Secondly, as shown in Figure 5, the first player puts “O” in the corner compartment (1,1) and the second player draws in the compartment (1,2). In this case, if the first player knows the strategy for this game for the N-position, he will put it in the compartment (3,3), and if the second player draws in the compartment (2,3), at this time, the first player only has one choice, that is, to put it in the compartment (3,2) or (1,2), which is the same. The second player will occupy the compartment (1,2), and the first player will lose. This is also known as a P-position.

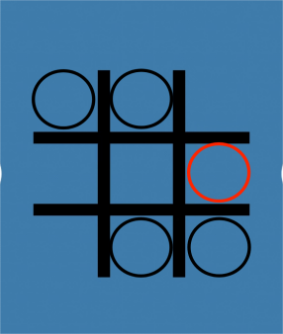
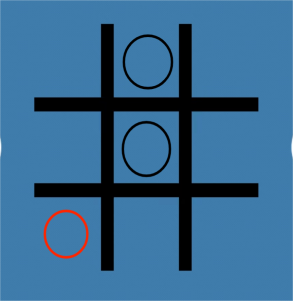
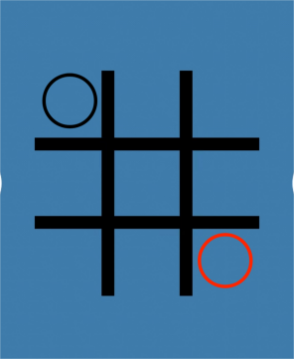
Thirdly, as illustrated in Figure 6, the first player puts it in the central compartment (2,2), and the second player puts it in the edge or the corner compartment (1,2). But if the first player puts his second point on the other side, for example, the compartment (3,1), then this is the difference between the first strategy and the second strategy. The opponent puts “O” in the compartment (3,3), and the first player can put the “O” in the compartment (2,3) to avoid forming a line. The opponent will lose, and the first player will win. This is known as the N-position (NP).

2.2. The maximizing winning strategy

As shown in Figure 7, there are only four lines in a 3 plus 3 square grid: the white one, the orange one, the green one, and the yellow one. According to the rule of this new game, one line can only be occupied by no more than two points. If one line is occupied by three points, the player will lose and the game will end. Thus, if the first player occupies the central compartment, all the lines in this 3 plus 3 square grid are occupied by one point. That means there will be only no more than 4 choices for the player later [4]. The first player always gets a strictly better score than the second one, but that the main factors is the center position [5].

Figure 7. The four kinds of lines that can be used in the reverse misère version.

The first player is supposed to keep as far as possible from the second player. If the first player puts his or her “O” too close to that of the second player, the remaining positions in the picture will be a waste and the choice will be given to the second player. After one player occupies the central compartment for the first move, the only strategy for another player is to “keep a distance” from the opponent in the second step. Then, in the following steps, because the remaining available positions must belong to the remaining available lines, there is no longer any position better than others. To keep a distance, the first player should try to put his or her point on the other side for the opponent’s point. For example, if the opponent puts it on the first row, the first player needs to put it on the third row's edge or corner [4]. If claiming the corner for the first move, to avoid the imitation of the second player, occupying the center is the most effective way.

The second player is supposed to keep close to the other player. For the first example, just keep close to the first player’s step and try to occupy the available position. But obviously, it is hard for the second player to win in the case that the first player puts his or her first step in the center and knows the strategy. The second example causes these because the center is empty. So every edge and corner is available to draw. And the second player needs to keep close to occupy the line near the first player, so the first player will have fewer choices to keep a distance. However, if the first player occupies the center at first, it is hard for the second player to be a winner in this game. In this kind of tic-tac-toe game, the center plays an extremely important role.

Besides, there is another explanation for the second game. It is like a mirror. The second player can use the mirror to imitate the first player. Because in this game, the center is empty, which means a line of the other two positions has to be occupied. And the center in this game is very important for the second player, determining whether he wins or not. So in this strategy, if the second player imitates the first player, the center will not be occupied. Eventually, it will form a graph that is symmetric along an oblique line from the top right to the bottom left.

As seen the Figure 8, if the first player occupies the compartment (1,1), the second player occupies the compartment (3,3), and then the first player finds a position that keeps a distance, for instance, the compartment (3,2) and the second player puts his second step in the compartment (2,1). At this time, the first player only has to put his step in the compartment (1,2), so the second player draws his step in the compartment (3,2). And the second player will win. This mirror way is a universal strategy in the combinatorial game for the second player to win.

3. Red-blue hackenbush games

3.1. Introduction about the rule

This section examines Red-Blue Hackenbush games under a normal play. Hackenbush games are played on a particular picture that is variable in shape and defined before the game, where players take turns choosing an edge of the partial order and removing every element above it and not connected with the ground. The roots induce a direction, towards the root, on each edge. A move is to delete a node, together with all nodes on the path to the root, and all edges incident with those nodes.The Left player can select Blue edges (the Right cannot) and the Right player can select Red elements (while the Left cannot). Red-Blue Hackenbush games have not attracted much attention in the literature, and most questions are about Green poset games (such as CHOMP) remaining open. Finally, the player who removes the last element will be the winner of the game [6].

3.2. The strategy

If "G" refers to a game of Red-Blue mis'ere Hackenbush and "B" and "R" stand for the number of blue and red edges that have each been grounded separately, the answer to "G" can be calculated using the following formula:

G∈L, if B>R(1)

R, if R>B(2)

N, if B=R(3)

Consider the situation where R>B if there are R grounded Red edges and B grounded Blue edges. First, consider the Left movement. Taking away one of his own grounded edges will be his or her winning maneuver. The Left may keep removing its grounded edges no matter what the Right does in reaction. The Left will prevail regardless of whether they move first or second in this scenario once they have eliminated all of these edges and there is at least one grounded Right edge.

The Right taking one of his grounded Red edges will be going to the situation R≥B, and it will be impossible for the Left to win moving second if R>B [3].

It is necessary to determine the outcome class for a game of Red-Blue mis'ere Hackenbush since the situation B≤R follows symmetry. The outcome class can be determined by simply counting the red and blue edges that are grounded and the difference. Red-Blue mis'ere Hackenbush is neither NP-complete nor NP-hard because it can be completed in polynomial time [3,7].

4. Conclusion

John Conway created the combinatorial games. Later, academics conduct extensive game theory research based on the variety of combinatorial games. Therefore, fresh concepts are always being proposed [6]. This work combines two categories of combinatorial games and extends the Reverse Misère variant of tic-tac-toe in a way that bases both players' strategies on whether they take the first step in the corner or the middle. However, many combinatorial games lack specialized strategies, making them NP-hard [8]. The two main categories of machine learning techniques for combinatorial optimization of NP-hard problems are supervised and reinforcement learning techniques.The two types of reinforcement learning techniques are model-free and model-based [9]. Additionally, there are still other variations of combinatorial games based on the standard form that call for scholars to combine game theory to come up with a winning strategy.