1. Introduction

Structural topology optimization aims to find the most effective way to distribute materials within a given domain in order to achieve a design objective. A vast array of fields, including mechanical design and other physical disciplines, were connected to this topic. To demonstrate the advantages and applications of structural topology optimization, a significant amount of research has been conducted and published over the past two decades. The homogenization approach, a numerical optimization technique proposed by Bendse and Kikuchi, serves as the starting point of this topic [1]. After the initial homogenization approach, additional numerical methods have been developed, leading to various directions. Density methods, evolutionary approaches, the level set method, and topological derivative method are the most common and developed approaches to structural topology optimization.

To overview and visualize the development of structural topology optimization, this paper gives a scientomeric analysis of the 5713 papers published from 2000 to 2022. Since there are various branches of topology optimization and it is impossible to cover all methods in one review, this paper aims to present a quantitative analysis over the whole topic and find out the most popular and influential approaches. A field of study called scientometrics can be used to measure and analyze scholarly literature; It is a research strategy that incorporates quantitative, qualitative, and computational methods. CiteSpace, one of the most widely used tools in this field, is used for the scientometric analysis in this paper. It can be used to investigate and visualize the impact of authors, journals, the frequency and relationship of key words, and other factors [2, 3].

This research is arranged as follows: Section one contains a broad introduction to the topic and the article. The data collecting and study technique were described in Section two. The findings of the scientometric analysis were shown in Section three. Section four introduces and discusses the most prominent methods from the Section three study. Finally, in the final part, the findings are given.

2. Data collection and research method

2.1. Data collection

This scientometric review relies entirely on the Web of Science core collection database for bibliographic data. This is due to CiteSpace outperforming other data sources when doing scientometric analysis on data from the Web of Science. Topic=("structural topology optimization" is the key phrase used in this topic's search term. Using the advanced refine option in Web of Science Categories, the non-structural topology optimization work was also removed. To be more exact, the outcome excluded any unnecessary characteristics such as heat. A total of 5713 bibliographic data, largely linked to the study topic, are included from January 2000 to August 2022.

2.2. Research method

CiteSpace 5.8.R3, a Java-based scientometric program, was utilized to conduct the scientometric analysis in this work. It might aid in discovering the latent meaning concealed in disorganized data and tracing its patterns and borders of growth. [3-5]. This study's scientific research employed three forms of bibliometric analysis: keyword co-occurrence, document co-citation analysis, and country co-occurrence. Co-word analysis may be used to examine word co-occurrences based on keywords and/or phrases. Authors, journals, and papers that have been co-cited can be detected using co-citation analysis. The research collaboration maps are also shown via co-occurrence analysis, or country co-occurrence.

3. Results and discussion

Figure 1 clearly depicted the increased trend in the yearly number of publications on the issue of structural topology optimization from 2000 to 2022, indicating that this field has become a notable hotspot in recent years. Since 2015, there has been an increase in the number of publications. The 2022 number was eliminated since those publications are only kept until August 2022.

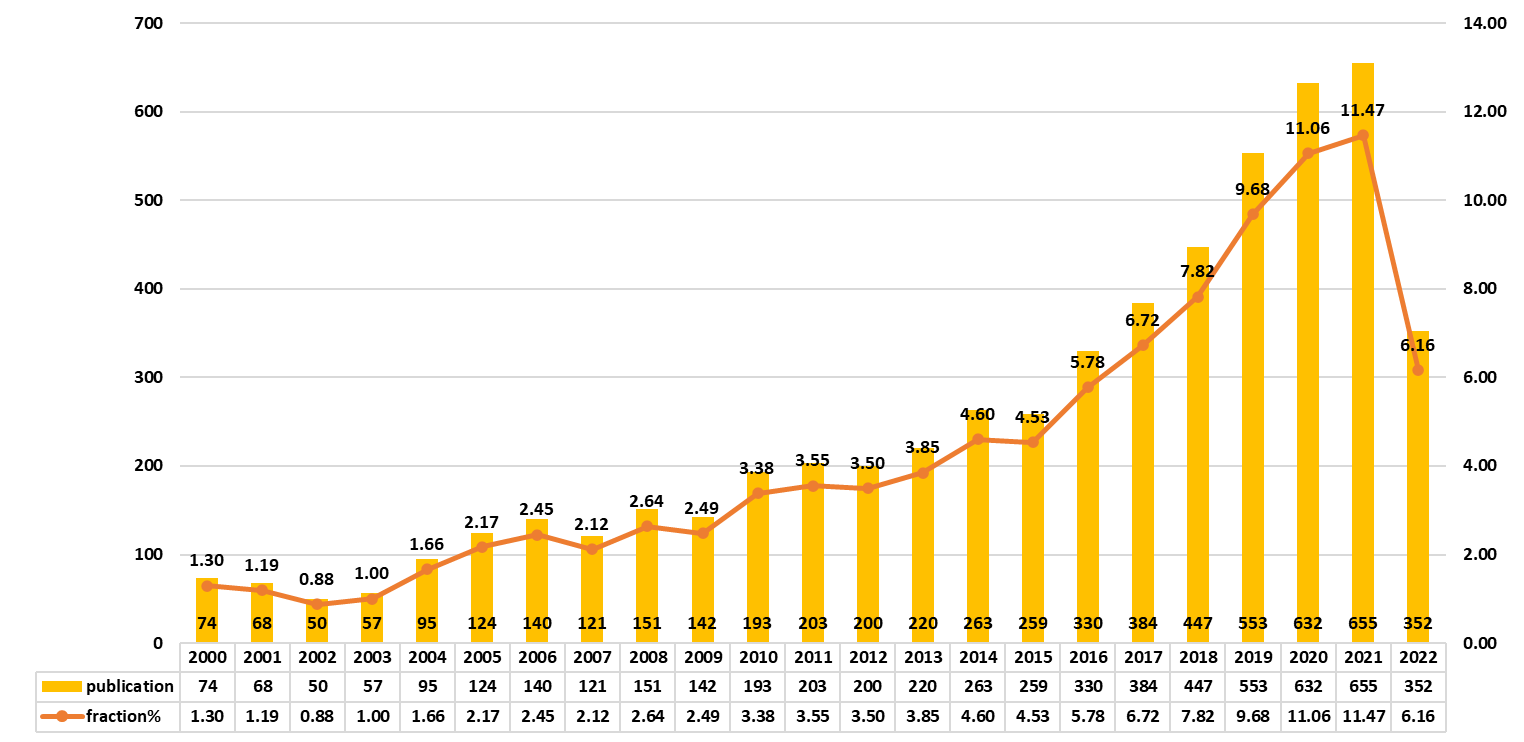
Figure 1. Number of publications under topic of structural topology optimization during 2000-2022 (the number in 2022 is only recorded till August).

In figure 2, the node size represents the keywords occurred frequency in this study. The top 10 key words with highest frequency of occurrence are: design (frequency=1780), topology optimization (frequency=1030), shape (frequency=566), algorithm (frequency=413), structural optimization (frequency=406), shape optimization (frequency=394), optimization (frequency=387), level set method (frequency=334), continuum structure (frequency=304), model (frequency=271), homogenization (frequency=242).

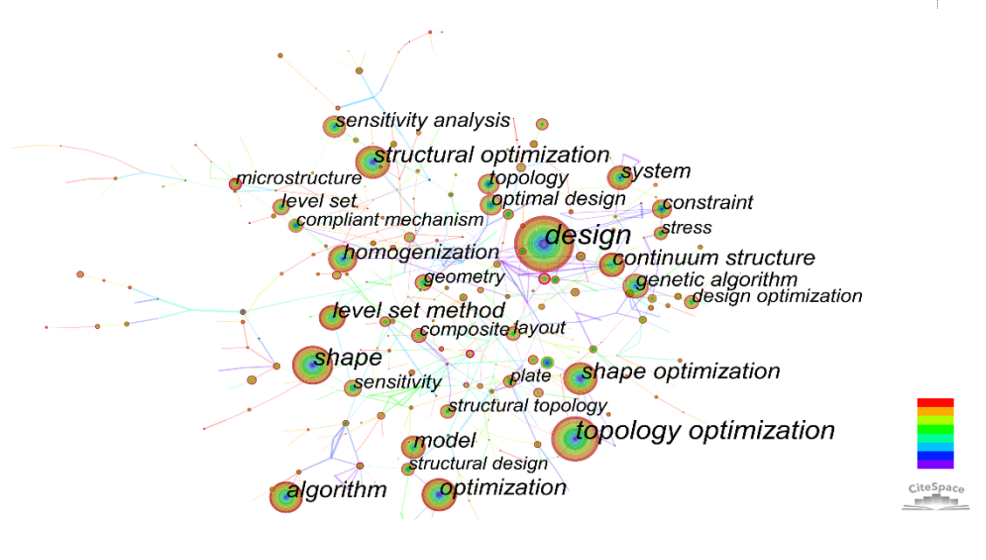
Figure 2. Key words co-occurrence.

To honor collaboration and contributions in terms of nation and/or area, a co-country/region network was also created. As indicated in Figure 3, the majority of papers in structural topology optimization have come from China, the United States, Australia, South Korea, Germany, and England. PEOPLES R CHINA (1711) and the United States of America (1086) both provide significantly more publications than other countries/regions. Furthermore, nodes in the network were highlighted with a purple circle, indicating that they provided critical contributions and connected the majority of countries/regions in this field.

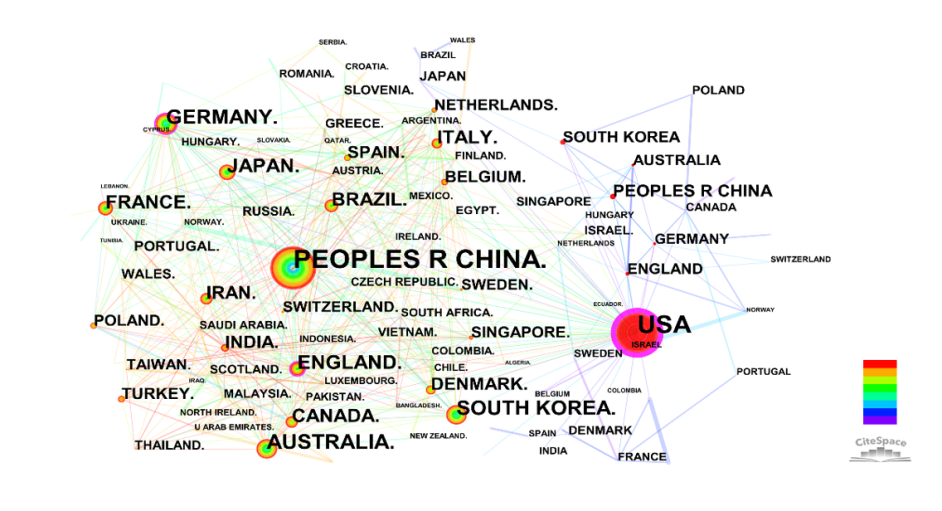
Figure 3. Network of countries/regions.

Co-citation analysis is a trustworthy and verified method for studying intellectual structure, and it plays a vital part in scientometric analysis. It is defined as the number of times two papers are referred by other texts [3, 6].

This study established a network of document co-citations. As shown in Figure 4, each node represents one article and is labeled with the initial author's name and the year of publication, while the node size denotes an article's co-citation frequency. The purple ring on the node in the document co-citation network indicates that the publication it represents is very important. Bendsoe MP has the most commonly co-cited works, however there are many more prominent publications in this subject shown in figure 4.

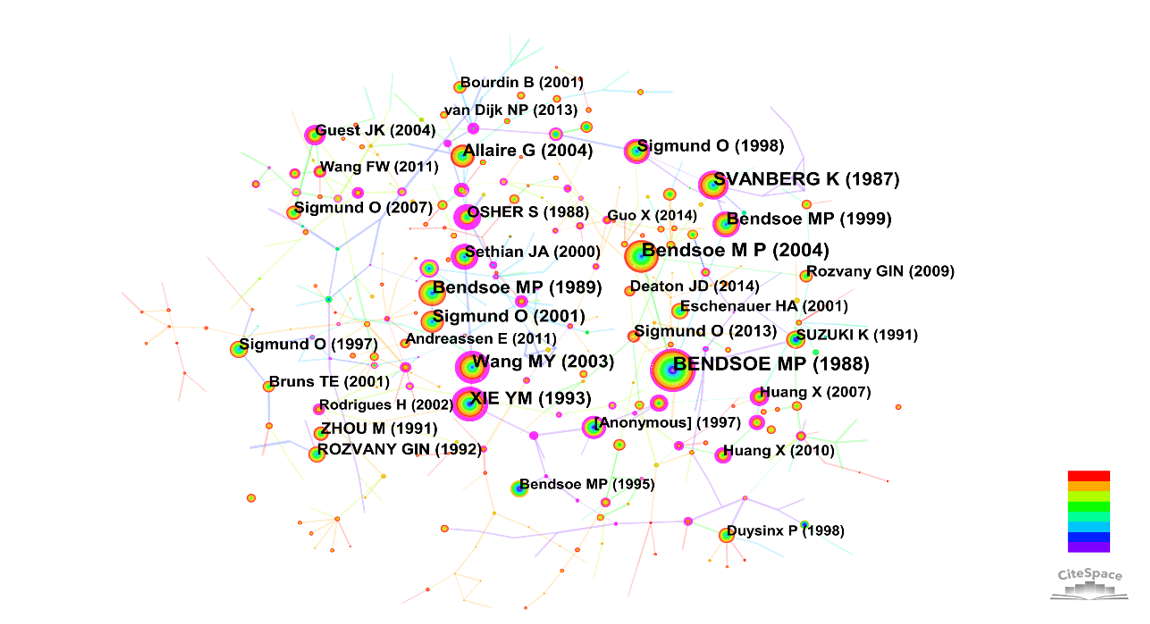
Figure 4. Co-citation map.

Top 10 most frequently co-cited papers are listed in table 1. In these most popular articles in structural topology optimization, number 1, 4, 8 are about density approaches; number 2 is about Topological derivative; number 5, 7, 9, 10 are about level set method; number 6 is about evolutionary approach. Number 3 is not about topology optimization, SVANBERG K proposed a truss sizing optimization method and is frequently co-cited in structural topology optimization studies.

Table 1. top 10 co-citation publications.

4. Main approaches

The volume fraction in density approaches can be any value between zero and one. Solid isotropic material with penalization model (SIMP) is based on density approach. In this model, a continuous variable \( ρ \) , \( 0≤ρ≤1 \) , is included, which resembles material density since the volume of the structure is assessed as

\( Vol=\int _{Ω}ρ(x)dΩ \) (1)

\( Ω \) is the full domain. [7].

Figure 5 is the cantilever beam topology optimization result for using SIMP method and Hashin-Shtrikman upper bound method.

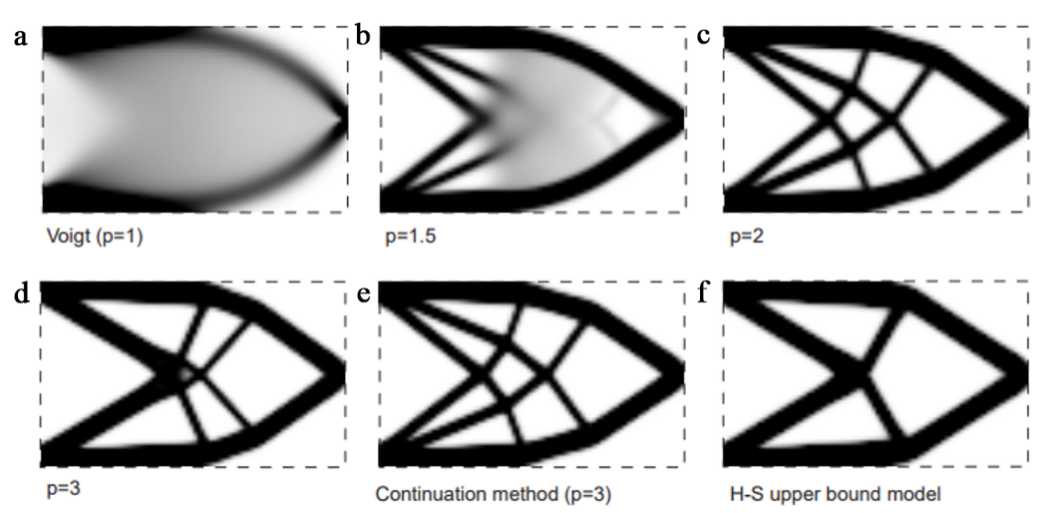
Figure 5: Optimal design findings for a cantilever beam for material and void, utilizing several powers of p in the SIMP interpolation technique and the Hashin-Shtrikman upper bound.

5a: Optimization results for the cantilever beam by using SIMP (p=1)

5b: Optimization results for the cantilever beam by using SIMP (p=1.5)

5c: Optimization results for the cantilever beam by using SIMP (p=2)

5d: Optimization results for the cantilever beam by using SIMP (p=3)

5e: Optimization results for the cantilever beam by using continuation method (p=3)

5f: Optimization results for the cantilever beam by using H-S upper bound model

The optimization in evolutionary approaches has evolved from basic hardkill tactics (elements with the lowest strain energy density are eliminated) until stress levels for all elements meet the target value [8-10]. In order to stabilize methods and findings, the idea currently employs typical adjoint gradient analysis and filtering techniques similar to those employed in the density approach. Figure 6 is an example of an evolutionary approach to optimizing a basic supported beam.

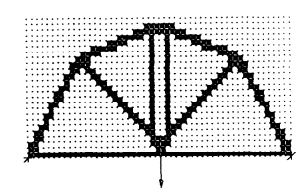
abc

Figure 6. Evolutionary optimization of a simple supported beam.

6a: Initial condition for the cantilever beam

6b: Optimization process for the cantilever beam

6c: Optimization results for the cantilever beam

In level set methods, the boundary of the design is defined by the zero level contour of the level set function \( ϕ(x) \) and the structure is defined by the domain where the level set function takes positive values. Figure 7 gives an example for level set method to conduct optimization for a cantilever beam [6] [11-13].

The border of the design is determined by the zero level contour of the level set function (x) in level set methods, and the structure is defined by the domain where the level set function takes positive values. Figure 7 shows an example of using the level set approach to optimize a cantilever beam [6] [11] [12] [13].

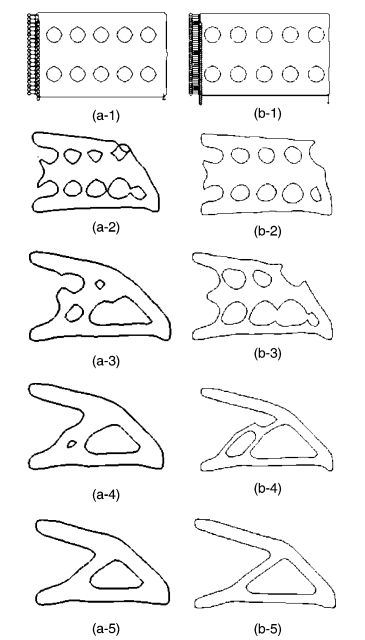
Figure 7. Optimization for the cantilever beam by the level set method.

7a-1,7b-1: Initial condition for the cantilever beam

7a-2, 7a-3, 7a-4, 7b-2, 7b-3, 7b-4: Optimization process for the cantilever beam

7a-5,7b-5: Optimization results for the cantilever beam

The essential idea behind the topological derivative method is to forecast the impact (derivative) of adding an infinitesimal hole at any location x in the design domain and use this as the driver for the development of further holes [9,14-16]. Figure 8 depicts the outcome of topological derivative optimization for a cantilever beam [9].

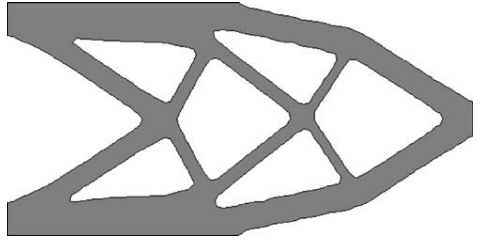
ab

Figure 8. Optimization for a cantilever beam by a topological derivative approach.

8a: Initial condition for the cantilever beam

8b: Optimization results for the cantilever beam

5. Conclusion

This study applied the scientometric technique to provide an overview of structural topology optimization articles from 2000 to 2020. the primary contributors by nation or area, as well as the most frequently referenced publications and research trends on certain themes are presented and discussed.

As previously stated, publications on structural topology optimization have increased substantially during the last two decades. Furthermore, this study highlighted the four methodologies employed as the key approaches developed for structural topology optimization in the top ten co-cited literatures.

The scientometric analysis relies on data obtained from Web of Science, which may not include all relevant publications on smart construction sites. Using multiple databases can provide a more comprehensive view of the research landscape. Further research directions could be to investigate the limitations and challenges of using structural topology optimization in practical engineering design and develop strategies to overcome them.