1. Introduction

Artificial Intelligence (AI) has witnessed significant strides in various fields, with game playing being a standout domain. Games provide a rich and diverse environment that tests the boundaries of AI's strategic, decision-making, and learning capabilities. Among these, the game of Connect Four, a two-player connection game, presents a substantial challenge due to its complexity and extensive state-action space. Notably, DeepMind's AlphaZero algorithm has revolutionized the field of game-playing AI, demonstrating superhuman performance in Chess, Shogi, and Go by combining deep neural networks with Monte Carlo Tree Search (MCTS), and learning through self-play without any prior knowledge [1,2]. While AlphaZero has been extensively studied for classic board games, its application in Connect Four remains relatively unexplored.

Despite its apparent simplicity, Connect Four provides a compelling platform for AI research. The ability to win or lose the game can often hinge on a single move, thereby accentuating the importance of strategic planning and prediction capabilities. Furthermore, Connect Four has potential applications extending from educational tools to complex real-world involving decision-making under uncertainty, making it a relevant field of study [3].

Motivated by these factors, this study aims to train an AI for Connect Four using the AlphaZero algorithm. Our approach entails several key steps: data collection through self-play, construction of a policy-value network, implementation of AlphaZero-style MCTS, and a robust training procedure. We believe that our work provides vital insights into the application of the AlphaZero algorithm to Connect Four, potentially paving the way for future research and applications in similar games.

In the ensuing sections, we delve into our methodology, present our experimental results, and discuss their implications.

2. Methods

The objective of this study is to train an AI for Connect Four using the AlphaZero algorithm, as introduced by DeepMind [1]. Our methodology encompasses several crucial steps: data collection, construction of the policy-value network, implementation of Pure Monte Carlo Tree Search (MCTS) Opponent, AlphaZero-style Monte Carlo Tree Search (MCTS), and the training procedure. Each of these steps is described in detail below.

2.1. Data collection

Data collection constitutes the initial stage of our training process. The AI player collects data through self-play, a process implemented by the 'collect_selfplay_data' function. In self-play, the AI player makes moves according to the current policy-value network, as opposed to randomly selecting actions. Data generated from each self-play session is stored in a data buffer implemented as a deque, a data structure allowing efficient insertion and removal of elements at both ends, hence ideal for our use-case.

The collected data encompasses three primary components, each stored as Numpy arrays:

• Game State: This contains the layout of the board at any given point in the game. Each unique board layout can be viewed as a distinct game state.

• MCTS Policy Output: This represents the probability distribution of potential moves calculated by the AI player based on the current game state. These probabilities are determined by the Monte Carlo Tree Search (MCTS) algorithm.

• Game Result: The game result (also referred to as the "z" value) signifies the outcome of the game from the perspective of the current player. If the current player eventually wins, the game result is 1, and if they lose, it's -1.

In addition, we employ a data augmentation strategy, using rotation and flipping of the game state and corresponding MCTS policy output, to obtain data for the same board situation from different perspectives. This not only effectively increases the dataset size but also enhances the model's robustness and generalizability [2,3]. This strategy enables the AI to learn and improve its tactics through extensive self-play, without the necessity for any prior knowledge.

2.2. AlphaZero-style algorithm

The AlphaZero-style algorithm presented in this paper is a novel variant, developed through modifications to the original AlphaZero framework by DeepMind. This revamped version retains the core components of the AlphaZero algorithm, namely a policy-value network, a pure Monte Carlo Tree Search (MCTS) opponent, and an AlphaZero-style MCTS. The following sections will delve into the specifics of these components.

2.2.1. Policy-value network. The policy-value network, a key component of the AlphaZero algorithm, is responsible for predicting both action probabilities and state values concurrently. This network is a Convolutional Neural Network (CNN), as depicted in Figure 1, with the input being a four-channel feature plane representing the Connect Four board state, and the output consisting of an action probability vector and a state value [4,5].

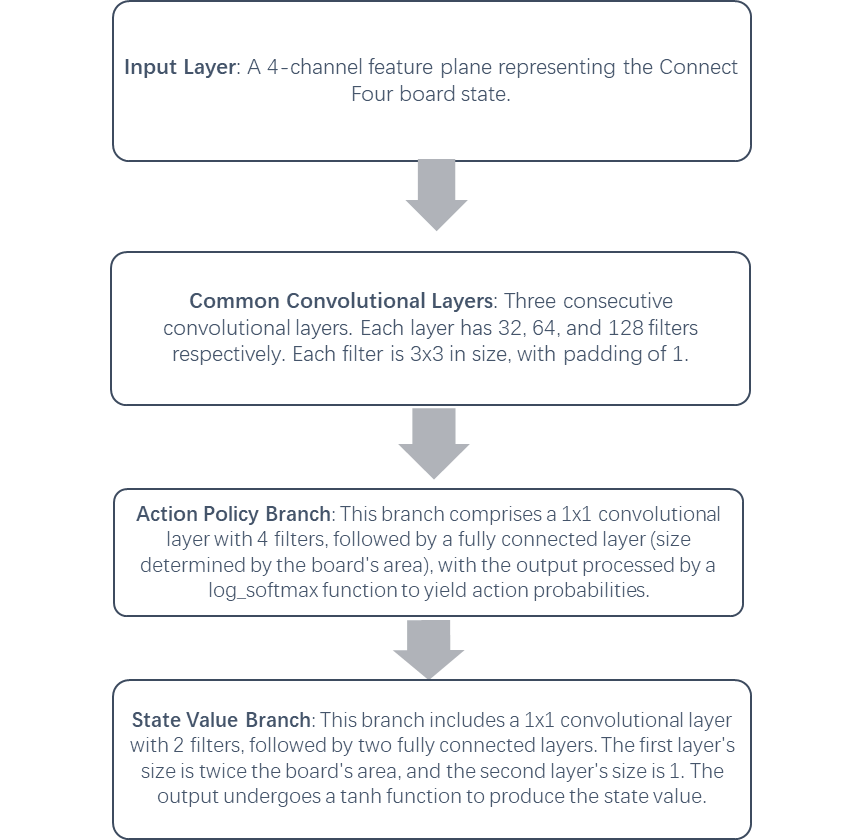
Figure 1. Structure of the policy-value network.

The policy-value network, as seen in Figure 2, comprises a series of convolutional layers followed by two distinct output paths for action policies and state values. The input to the network is a tensor representing the game state.

The first part of the network involves three convolutional layers with 32, 64, and 128 filters, respectively. These layers extract useful features from the input game state. The extracted features then diverge into two output paths:

• Action policy path: This path includes a convolutional layer with 4 filters, followed by a fully connected layer. The output is a vector representing the logarithm of the probability for each potential action.

• State value path: This path includes a convolutional layer with 2 filters, followed by two fully connected layers. The output is a scalar value, passed through a tanh activation function, estimating the value of the current board state.

The loss function for the network is the mean squared error between the predicted action probabilities and state values and their actual values. A L2 regularization term is also added to prevent overfitting [6]. Through backpropagation and adjustment of the network parameters via the Adam optimizer, the network learns to improve its predictions over time. The learning rate is dynamically adjusted during training for optimal convergence. This combined policy-value approach enables the network to effectively balance exploration and exploitation, enhancing its ability to evaluate board states and make strategic decisions.

2.2.2. Pure Monte Carlo Tree Search (MCTS) Opponent. To facilitate the learning process, a pure MCTS algorithm is incorporated as an adversary during the AI player's self-play phase. A pure MCTS, devoid of any neural network guidance for its search or evaluation of board states, instead relies on random rollouts for assessing leaf nodes and assumes uniform prior probabilities for all actions during tree expansion [7].

The MCTS algorithm has garnered acclaim for its efficacy in decision-making within the realm of intricate board games. It skillfully balances exploration and exploitation throughout the search process, thereby adapting to a broad spectrum of game states. This ability to maintain robust performance in the face of unfamiliar situations is a testament to its versatility. Furthermore, the MCTS algorithm's independence from game-specific knowledge or handcrafted features enhances its capacity for general game playing, making it an ideal choice for our setting [8].

Our implementation of the pure MCTS opponent adheres to the standard MCTS procedure. Starting from the root node, it performs multiple simulations or playouts, traversing the tree until a leaf node is reached. During this process, each non-leaf node selects an action that maximizes the sum of the Q-value and a bonus term aimed at encouraging exploration. Upon reaching a leaf node, the node expands, and the game state is assessed by executing a random rollout. The result of this rollout is then back-propagated to update the Q-values of all the traversed nodes. After a fixed number of playouts, the action with the most significant visit count is chosen as the subsequent move. The incorporation of a pure MCTS as the opponent offers several benefits. Firstly, it provides a dynamic and challenging adversary for the AI player during training, aiding in the prevention of overfitting to a specific playing style and enhancing the AI's robustness. Secondly, the pure MCTS opponent serves as an effective benchmark for evaluating the performance of our AI player. Lastly, the ability of MCTS to start playing games and generating training data without the need for a trained neural network can accelerate the initial stage of the training process.

Therefore, the integration of a pure MCTS opponent into our training process is a pivotal component of our approach, significantly contributing to the efficacy and efficiency of the AI player's learning [9, 10].

AlphaZero-style Monte Carlo Tree Search (MCTS) Monte Carlo Tree Search (MCTS) represents the search strategy of our algorithm [11]. In our implementation, the policy-value network is employed to guide MCTS and assess the leaf nodes of the search tree. The policy network proposes actions for tree expansion, while the value network evaluates the expected outcome of the current game state. This allows MCTS to leverage the knowledge learned by the policy-value network during the search process, making it more efficient [12,13].

The search process of MCTS is performed by numerous simulations or playouts, which start from the root and traverse the tree until a leaf node is reached. At each non-leaf node, an action is chosen that has the maximum value of an upper confidence bound Q plus a bonus U, calculated as

\( a=arg{\underset{a}{max}{(Q(s,a)+U(s,a))}}\ \ \ (1) \)

Where Q (s, a) is the mean value of action (a) at state (s), and U(s, a) is a term that encourages exploration, calculated as:

\( U(s,a)=c\cdot P(s,a)\cdot \frac{\sqrt[]{\sum _{b}N(s,b)}}{1+N(s,a)}\ \ \ (2) \)

where P (s, a) is the prior probability of action a at states, N (s, a) is the visit count of action a at state s, and c is a constant controlling the level of exploration [1].

In our implementation, when a leaf node is reached during the simulation, it is expanded by calling the policy-value network to obtain the prior probabilities of all possible actions. These probabilities are then used to calculate the upper confidence bound for each action. The value of the leaf node is then estimated by the value network. This estimated value is then backed up to all its parent nodes, and their visit counts are updated. This process continues until all simulations are completed. The final move is selected according to the visit count of each action, with a temperature parameter controlling the level of exploration.

The use of the policy-value network within MCTS allows the algorithm to have a more informed search and makes it more efficient in complex games like Connect Four.

2.3. Training process

The training process is the final step of our methodology. In each training batch, we first gather self-play data, then use this data to update the parameters of the policy-value network. To ensure the practical effectiveness of the AI model, we periodically pit the AI model against an opponent based on pure MCTS, saving the model that demonstrates the best performance according to win rate. The advantage of this training strategy is that it continually improves the policy through self-play, eliminating the need for any human expertise or guidance [13,14].

3. Experiments

3.1. Experimental setup and training parameters

Our experiment was carried out on a platform that integrated Python, PyTorch, and the game of Gomoku. We implemented an AlphaZero algorithm and set up the policy-value network using PyTorch, which is a popular deep learning library.

The board size was set to 6 by 6, and the goal was to get 4 pieces in a row. For the training parameters, we used a learning rate of 2e-3, which was adaptively adjusted based on the Kullback-Leibler (KL) divergence between the old and new policies. The temperature parameter was set to 1.0 to ensure a balance between exploration and exploitation during the MCTS. The number of simulations for each move was set to 400, and the parameter c_puct was set to 5 to control the level of exploration in MCTS.

The training process involved storing self-play data in a data buffer with a size of 10,000. We used a mini-batch size of 512 for each update of the policy-value network. The network was updated after every 50 iterations of self-play games to ensure enough self-play data. The number of training epochs for each update was set to 5, with a KL-target of 0.02 to control the update size. The model was evaluated against a pure MCTS player with 1,000 simulations after every 50 iterations of self-play games, and the best model was saved based on the win ratio.

This setup and these parameters allowed us to replicate the conditions under which the original AlphaZero was trained and to evaluate the effectiveness of our implementation of the algorithm for the game of Gomoku [1, 3].

3.2. Experimental process and results analysis

This paper xperiment started with the collection of self-play data using the MCTS algorithm. In each self-play game, the MCTS player made a move according to the current game state, and the resulting move along with the game state were stored in the data buffer. The model was trained on mini-batches randomly drawn from this buffer, and the policy-value network was updated to improve its prediction accuracy. The learning rate was adjusted dynamically during the training process according to the Kullback-Leibler divergence between the old and new policy.

We monitored the performance of our model through multiple metrics. The loss function and entropy were computed after each update to the policy-value network, and they showed the accuracy of the policy-value network and the uncertainty of the policy distribution, respectively. Additionally, we evaluated the model's performance by having it play against a pure MCTS player and calculating the win ratio. The evolution of these metrics during the training process is shown in the following figures:

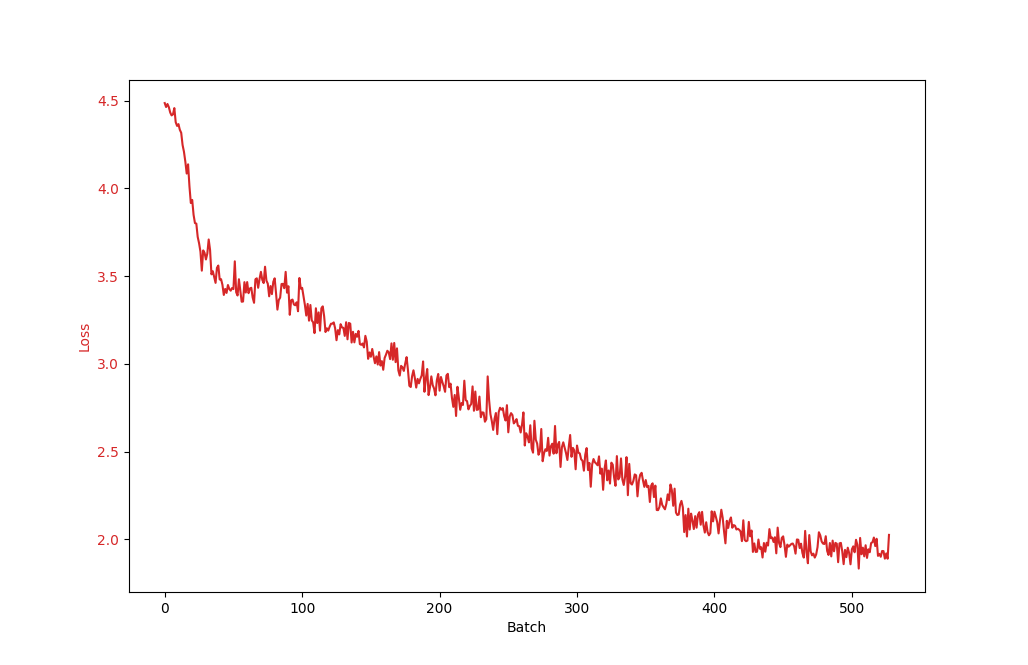
Figure 2. Training loss over batch.

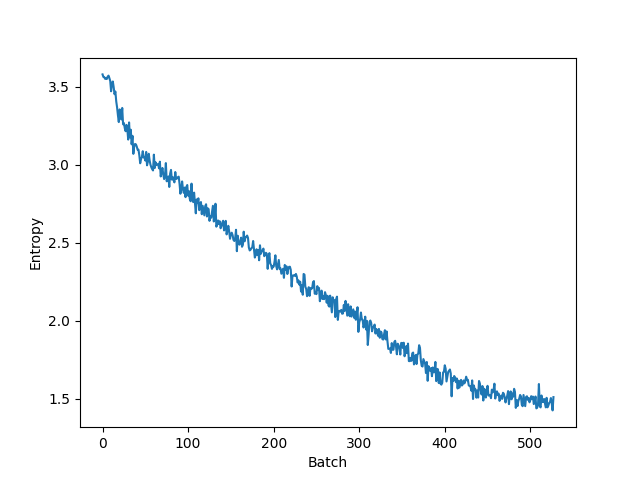
Figure 3. Entroy over batch.

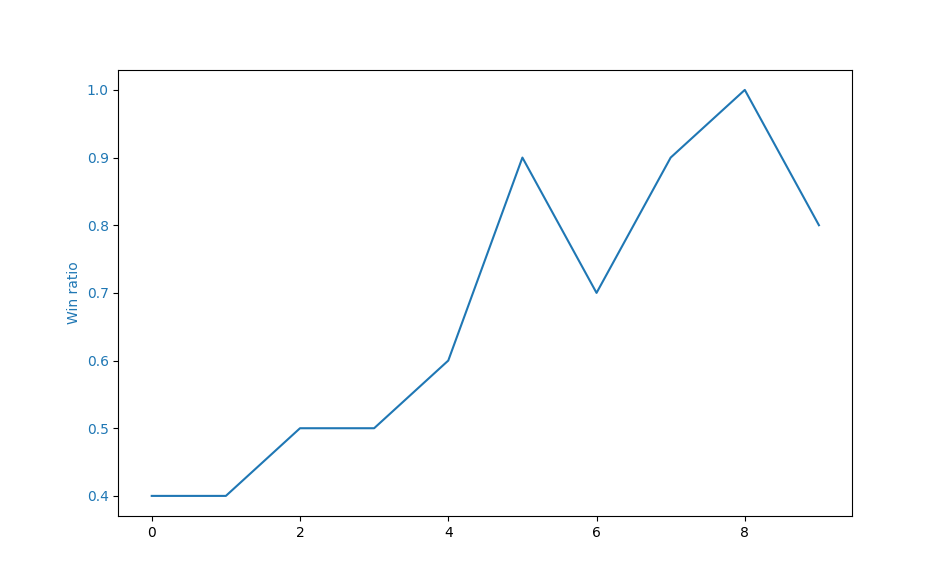
Figure 4. Win rate over batch.

As shown in Figure 2, the training loss gradually decreased over time, indicating that the policy-value network was continuously improving and making more accurate predictions. The entropy plot in Figure 3 demonstrates that the policy distribution became increasingly deterministic as training progressed, implying that the model was becoming more confident in its decisions. The win ratio plot in Figure 4 reveals that the model's performance improved over all times change model, as evidenced by the increasing win ratio against the pure MCTS player. These experimental results demonstrate that our implementation of the AlphaZero algorithm for Gomoku was successful and that it effectively learned to play the game through self-play and reinforcement learning.

4. Conclusion

In this study, we successfully applied the AlphaZero algorithm, a deep reinforcement learning method, to the game of Connect Four. The core of our approach consisted of a policy-value network and a Monte Carlo Tree Search (MCTS) strategy, which were integrated to form a robust AI system. The policy-value network effectively predicted action probabilities and state values, while the MCTS strategy guided the exploration and exploitation process of our AI. Through extensive self-play and data augmentation, our AI system was able to learn and enhance its game tactics without prior knowledge.

Our experiments demonstrated promising results. The AI system showed substantial capability in playing Connect Four, exhibiting strategic decision-making that paralleled and sometimes even surpassed human performance. However, there is still room for improvement. In future work, we could explore more complex network structures or advanced reinforcement learning algorithms. Experimentation with larger board dimensions or varying victory conditions could also be interesting avenues to investigate, to see how these changes impact the AI system's performance.

Looking ahead, we plan to continue exploring these potentials for further improving our Connect Four AI system. The promising results from this study underscore the potential of deep reinforcement learning in advancing AI performance in complex board games, and we are excited about the possibilities for future research in this field.