1. Introduction

Against the backdrop of rural revitalization, cold chain logistics, which plays a crucial role in promoting agricultural product sales and driving agricultural development, has become a focal point of attention across various sectors of society. The issuance of the "14th Five-Year Plan for the Development of Cold Chain Logistics" by the State Council Office at the end of 2021 not only emphasizes the strategic importance of cold chain logistics development but also signals the nation's commitment to vigorously promote its development within the context of the new development paradigm. Despite the gradual development of cold chain logistics in China, the industry is still in its early stages, facing numerous challenges that hinder its ability to meet the growing demand for agricultural products [1].

Numerous domestic and international scholars have conducted extensive research around the theme of this paper, primarily focusing on: (1) Optimization of strategic interactions between participants in cold chain logistics. Zhu Lilong and Guo Pengfei, based on game theory, established both pure strategic and mixed strategic game models between the government and cold chain food enterprises. They explored the game relationship between the two and analyzed their optimal strategic choices under different scenarios [2]. Addressing the prevalent issue of information asymmetry in the fresh agricultural product market, Xu Yaoqun et al. constructed an evolutionary game model for online fresh agricultural product network stores and logistics service providers under the online shopping model [3]. (2) Evolutionary game models involving three participants in cold chain logistics. Li Chunfa et al. focused on the supply chain involving two agricultural product e-commerce platforms, self-operated cold chain logistics of e-commerce platforms, and third-party cold chain logistics providers. They developed Stackelberg game models for competition between the two e-commerce platforms and an evolutionary game model for the selection of cold chain logistics modes by the two e-commerce platforms [4]. Zhang Yuehua et al. examined the cold chain logistics platform ecosystem as a whole, elucidating the complex interactions among its components. They studied the impact of dynamic cooperative relationships among system entities on the evolution of the cold chain logistics platform ecosystem from the perspective of evolutionary games [5]. (3) Stochastic evolutionary games involving three participants. Yang Yaohong et al. introduced Gaussian white noise as a random disturbance into the evolutionary game, exploring quality management issues in the construction project supply chain [6]. Addressing manipulation phenomena in the application process for high-tech research and development, Li Junqiang et al. constructed a three-party stochastic evolutionary game model and simulated the impact of key variables on the strategic choices of participating entities [7].

From the above, it is evident that early research on cold chain logistics game optimization primarily focused on pairwise interactions between government, enterprises, and third-party inspection agencies. As research deepened, attention gradually shifted to multi-agent collaborative optimization from the perspective of evolutionary games to better align with real-world scenarios. Moreover, considering that evolutionary games are susceptible to uncertainties such as individual cognition, risk preferences, and environmental factors, the introduction of stochastic systems into multi-agent evolutionary games is gaining increasing attention from scholars both domestically and internationally. However, existing research has mainly concentrated on areas such as technology research and development, construction, and food safety and regulation. Therefore, establishing a three-party game model involving farmers, logistics enterprises, and government regulatory authorities holds significant importance for the development of cold chain logistics in agricultural products.

2. Model Assumptions and Construction

Cold chain transportation involves a dynamic game optimization process with multiple participants. Specifically, it can be described as follows: (1) To ensure the quality and freshness of agricultural products for subsequent transportation, farmers, who serve as the "first mile" in agricultural cold chain logistics, need to conduct pre-cooling processing on harvested agricultural products. (2) Acting as the transportation party linking farmers and consumers, logistics enterprises adjust and monitor the temperature and humidity throughout the transportation process. This requires the establishment of sound cold chain facilities and the construction of an intelligent cold chain logistics information platform. (3) Government regulatory departments supervise farmers and logistics enterprises to promote the development of the cold chain.

However, due to the generally high purchase cost of cold chain facilities and limited awareness of cold chain among farmers, farmers and logistics enterprises seeking to maximize their own interests may choose not to invest in cold chain. Additionally, in the era of new media, public opinion and reputation can lead to varying degrees of regulatory leniency.

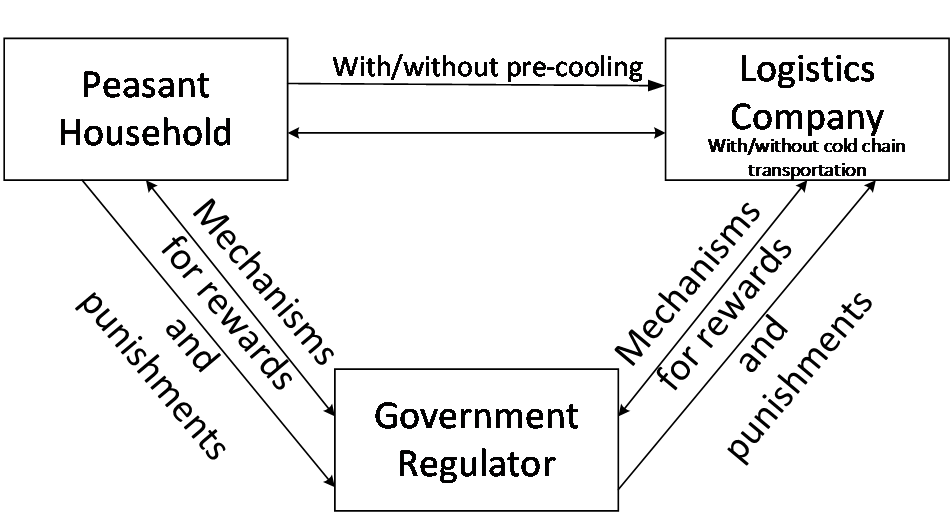
Figure 1: Supply Chain Participant Relationships

2.1. Basic Model Assumptions

(1) In the game model, the three parties choose strategies based on their own preferences. It is assumed that the probability of farmers choosing regular processing is \( x(0≤x≤1) \) , and the probability of pre-cooling processing is \( 1-x \) . The probability of logistics enterprises adopting regular transportation is \( y(0≤y≤1) \) , and the probability of adopting cold chain logistics transportation is \( 1-y \) . The government regulatory department's probability of choosing strict regulation is \( z(0≤z≤1) \) , and the probability of choosing lenient regulation is \( 1-z \) .

(2) The basic income for farmers is \( {R_{f}} \) , and the cost for adopting pre-cooling or regular processing is \( {C_{fh}} \) and \( {C_{fl}} \) \( ({C_{fh}} \gt {C_{fl}}) \) . The basic income for logistics enterprises is \( {R_{e}} \) , and the cost for adopting cold chain or regular logistics transportation is \( {C_{eh}} \) and \( {C_{el}} \) \( ({C_{eh}} \gt {C_{el}}) \) . The social benefit brought by adopting cold chain technology for transportation is \( {V_{g}} \) . The additional income when farmers adopt pre-cooling processing and logistics enterprises adopt cold chain transportation is \( ΔR \) .

(3) Under strict government regulation, rewards are given to farmers adopting pre-cooling processing and logistics enterprises adopting cold chain transportation, denoted by \( {G_{f}}、{G_{e}} \) . For farmers adopting regular processing and logistics enterprises employing regular transportation: Impose fines \( F \) and require them to upgrade to cold chain transportation. After the upgrade, the quality of agricultural products is assumed to be the same as when cold chain resources are invested. The cost of cold chain upgrading is denoted as \( α \) times the cost, i.e., \( α{C_{fl}} \) and \( α{C_{el}} \) . In addition, logistics enterprises utilizing cold chain transportation will inspect the agricultural products of farmers and demand that farmers who did not adopt pre-cooling processing upgrade to cold chain transportation. In this case, the upgrading cost for farmers is denoted as \( α{C_{fl}} \) . The cost for the government regulatory department to impose strict supervision is denoted as \( {C_{g}} \) .

(4)Under lenient government regulation, with no knowledge of supply chain decision choices, there are no rewards or penalties. If farmers or logistics enterprises do not adopt pre-cooling processing or cold chain transportation, it leads to a reputation loss \( {D_{g}} \) . Additionally, a certain transmission coefficient \( β \) transfers the loss to farmers and logistics enterprises.

(5)When neither farmers nor logistics enterprises invest in cold chain resources, and the government chooses lenient regulation, the probability of damage to the quality of agricultural products is maximum, assumed to be 1. If one party invests in cold chain resources, the probability of damage to the quality of agricultural products is reduced with discount factors \( {L_{f}} \) and \( {L_{e}} \) . If both farmers and logistics enterprises invest in cold chain resources, the probability of damage to the quality of agricultural products is minimized, assumed to be 0.

2.2. Construction of the Payoff Matrix

Based on the above description of the three-party game and the related assumptions, the payoff matrix for the game is presented in Table 1:

Table 1: Payoff Matrix for the Three-Party Game Involving Farmers, Logistics Enterprises, and Government Regulatory Department

Based on the payoff matrix, the expected payoffs \( {U_{11}} \) , \( {U_{12}} \) , and \( \overline{{U_{1}}} \) for farmers, as well as the strategy replication dynamic equations, are derived as follows:

\( \begin{cases} \begin{array}{c} {U_{11}}=yz({R_{f}}-{C_{fl}}-β{D_{g}})+y(1-z)({R_{f}}-(1+α){C_{fl}}-F)+(1-y)z[{R_{f}}-(1+α){C_{fl}}-{L_{f}}β{D_{g}}]+(1-y)(1-z)[{R_{f}}-(1+α){C_{fl}}-F] \\ {U_{12}}=yz({R_{f}}-{C_{fh}}-{L_{e}}β{D_{g}})+y(1-z)({R_{f}}-{C_{fh}}+{G_{f}})+(1-y)z({R_{f}}+ΔR-{C_{fh}})+(1-y)(1-z)({R_{f}}-{C_{fh}}+{G_{f}}) \\ \overline{{U_{1}}}=x{U_{11}}+(1-x){U_{12}} \end{array} \end{cases} \)

\( F(x)=\frac{dx}{dt}=x({U_{11}}-\overline{{U_{1}}})=x(1-x)[{C_{fh}}-{C_{fl}}-F-{G_{f}}-{C_{fl}}α+z(F+{G_{f}}-R-{D_{g}}{L_{f}}β)+yz(R+{C_{fl}}α-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)] \) (1)

Based on the payoff matrix, the expected payoffs \( {U_{11}} \) , \( {U_{12}} \) , and \( \overline{{U_{1}}} \) for logistics enterprises, as well as the strategy replication dynamic equations, are derived as follows:

\( \begin{cases} \begin{array}{c} {U_{21}}=x[z({R_{e}}-{C_{el}}-β{D_{g}})+(1-z)({R_{e}}-(1+α){C_{el}}-F)]+(1-x)[z({R_{e}}-{C_{el}}-{L_{e}}β{D_{g}})+(1-z)({R_{e}}-(1+α){C_{el}}-F)] \\ {U_{22}}=x[z({R_{e}}-{C_{eh}}-{L_{f}}β{D_{g}})+(1-z)({R_{e}}-{C_{eh}}+{G_{e}})]+(1-x)[z({R_{e}}+ΔR-{C_{eh}})+(1-z)({R_{e}}-{C_{eh}}+{G_{e}})] \\ \overline{{U_{2}}}=y{U_{21}}+(1-y){U_{22}} \end{array} \end{cases} \)

\( F(y)=\frac{dy}{dt}=y({U_{21}}-\overline{{U_{2}}})=y(1-y)[{C_{eh}}-{C_{el}}-F-{G_{e}}-{C_{el}}α+z(F+{G_{e}}-R+{C_{el}}α-{D_{g}}{L_{e}}β)+xz(R-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)] \) (2)

Based on the payoff matrix, the expected payoffs \( {U_{11}} \) , \( {U_{12}} \) , and \( \overline{{U_{1}}} \) for the government regulatory department, as well as the strategy replication dynamic equations, are derived as follows:

\( \begin{cases} \begin{array}{c} {U_{31}}=xy(-{D_{g}})+x(1-y)({V_{g}}-{L_{f}}{D_{g}})+(1-x)y({V_{g}}-{L_{e}}{D_{g}})+(1-x)(1-y){V_{g}} \\ {U_{32}}=xy({V_{g}}-{C_{g}}+2F)+x(1-y)({V_{g}}-{C_{g}}+F-{G_{e}})+(1-x)y({V_{g}}-{C_{g}}+F-{G_{f}})+(1-x)(1-y)({V_{g}}-{C_{g}}-{G_{f}}-{G_{e}}) \\ \overline{{U_{3}}}=z{U_{31}}+(1-z){U_{32}} \end{array} \end{cases} \)

\( F(z)=\frac{dz}{dt}=z({U_{31}}-\overline{{U_{3}}})=z(z-1)[-{C_{g}}-{G_{f}}-{G_{e}}+x({G_{f}}+F+{D_{g}}{L_{f}})+y({G_{e}}+F+{D_{g}}{L_{e}})+xy({D_{g}}+{V_{g}}-{D_{g}}{L_{e}}-{D_{g}}{L_{f}})] \) (3)

3. Construction of Stochastic Evolutionary Game

Due to the non-negative nature of \( x,y,z∈[0,1] \) , \( 1-x \) , \( 1-y \) and \( 1-z \) , which do not affect the evolutionary strategy choices of all parties, equations (1), (2), and (3) can be simplified as follows:

\( dx=x[{C_{fh}}-{C_{fl}}-F-{G_{f}}-{C_{fl}}α+z(F+{G_{f}}-R-{D_{g}}{L_{f}}β)+yz(R+{C_{fl}}α-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)]dt \) (4)

\( dy=y[{C_{eh}}-{C_{el}}-F-{G_{e}}-{C_{el}}α+z(F+{G_{e}}-R+{C_{el}}α-{D_{g}}{L_{e}}β)+xz(R-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)]dt \) (5)

\( dz=z[-{C_{g}}-{G_{f}}-{G_{e}}+x({G_{f}}+F+{D_{g}}{L_{f}})+y({G_{e}}+F+{D_{g}}{L_{e}})+xy({D_{g}}+{V_{g}}-{D_{g}}{L_{e}}-{D_{g}}{L_{f}})]dt \) (6)

3.1. Random Disturbance Factors on Entities

In the actual cold chain system, there is significant uncertainty in the game between farmers, logistics enterprises, and government regulatory departments. On one hand, due to differences in cognitive abilities, risk preferences, and other factors, game entities may have various possibilities for strategic choices. On the other hand, factors such as the biological attributes of agricultural products can also influence the strategic choices of entities. Therefore, utilizing stochastic analysis theory, Gaussian white noise is introduced to describe the random disturbance factors in the agricultural product cold chain system. The modified replicator dynamic equations are then given as follows:

\( dx=x[{C_{fh}}-{C_{fl}}-F-{G_{f}}-{C_{fl}}α+z(F+{G_{f}}-R-{D_{g}}{L_{f}}β) \) \( +yz(R+{C_{fl}}α-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)]dt+σx(t)dω(t) \) (7)

\( dy=y[{C_{eh}}-{C_{el}}-F-{G_{e}}-{C_{el}}α+z(F+{G_{e}}-R+{C_{el}}α-{D_{g}}{L_{e}}β) \) \( +xz(R-{D_{g}}β+{D_{g}}{L_{e}}β+{D_{g}}{L_{f}}β)]dt+σy(t)dω(t) \) (8)

\( dz=z[-{C_{g}}-{G_{f}}-{G_{e}}+x({G_{f}}+F+{D_{g}}{L_{f}})+y({G_{e}}+F+{D_{g}}{L_{e}}) \) \( +xy({D_{g}}+{V_{g}}-{D_{g}}{L_{e}}-{D_{g}}{L_{f}})]dt+σz(t)dω(t) \) (9)

Equations (7), (8), and (9) represent one-dimensional \( It\hat{o} \) stochastic differential equations, indicating the evolutionary replicator dynamic equations for farmers, logistics enterprises, and government regulatory departments after being subjected to random disturbances. Here, \( σ \) is the intensity of the random disturbance, and \( ω(t) \) is a one-dimensional standard \( Brown \) Wiener process. When \( t \gt 0 \) , \( h \gt 0 \) , the increment \( Δω(t)=ω(t+h)-ω(t) \) follows a normal distribution \( N(0,\sqrt[]{h}) \) .

4. Numerical Experiments and Simulations

To intuitively illustrate the stochastic evolutionary process of the cold chain supply chain, we use Matlab R2017b to analyze the impact of relevant parameters on the evolutionary process. Due to the inability to directly solve nonlinear \( It\hat{o} \) stochastic differential equations, we use Euler's method for numerical simulation of the model [6]. Considering the complexity and unavailability of real data, we refer to relevant studies such as [6-7]. We set the initial probability choices of all participating entities to 0.5 and assign values to other relevant parameters based on satisfying the conditions for the zero solution matrix instability, as follows: \( {R_{f}}=50 \) , \( {R_{e}}=80 \) , \( ΔR=5 \) , \( {C_{fh}}=15 \) , \( {C_{fl}}=6 \) , \( {C_{eh}}=15 \) , \( {C_{el}}=6 \) , \( {C_{g}}=35 \) , \( {V_{g}}=20 \) , \( {G_{f}}=8、{G_{e}}=8 \) , \( F=6 \) , \( {D_{g}}=20 \) , \( {L_{f}}=0.6 \) , \( {L_{e}}=0.3 \) , \( α=0.1 \) , \( β=0.5 \) .

4.1. Impact of Random Disturbances on the Evolutionary Process

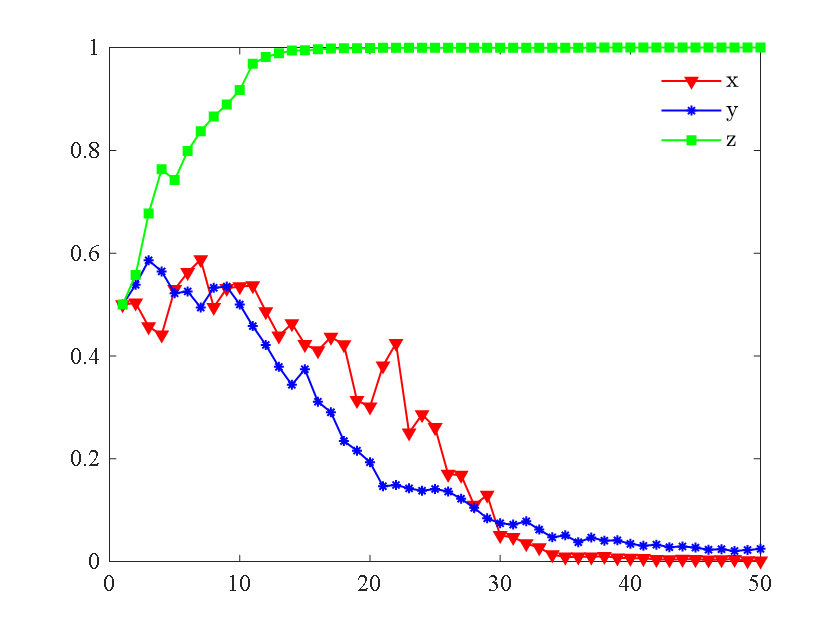
Comparing Figures 2 and 3, it can be observed that regardless of the presence of random disturbance factors, all entities will evolve to a stable equilibrium strategy set (pre-cooling, cold chain transportation, strict regulation). When there is no random interference, the system smoothly evolves to a stable equilibrium strategy set, indicating an idealized system. However, with the introduction of random disturbance factors, the system shows varying degrees of fluctuations. This is because various entities seeking to maximize their interests consider these uncertain factors influenced by internal factors such as the cognitive abilities of farmers and the risk preferences of enterprises, as well as external factors such as weather and changes in government subsidy policies. This leads to the phenomenon of non-uniform actions within the group.

Government regulatory departments evolve to a stable strategy faster than farmers and logistics enterprises. This is because of information asymmetry among the three entities, where government regulatory departments hold an advantageous position in the cold chain system, possessing more information and resources compared to farmers and logistics enterprises. Leveraging this advantageous position allows government regulatory departments to make optimal choices more quickly and evolve to a stable strategy at a faster pace.

4.2. Impact of Random Disturbance Intensity on the Evolutionary Process

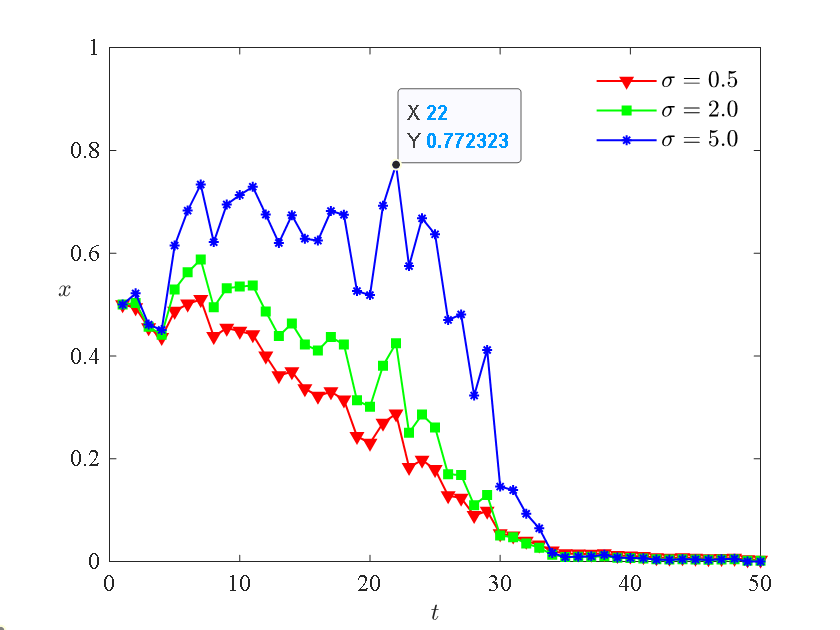
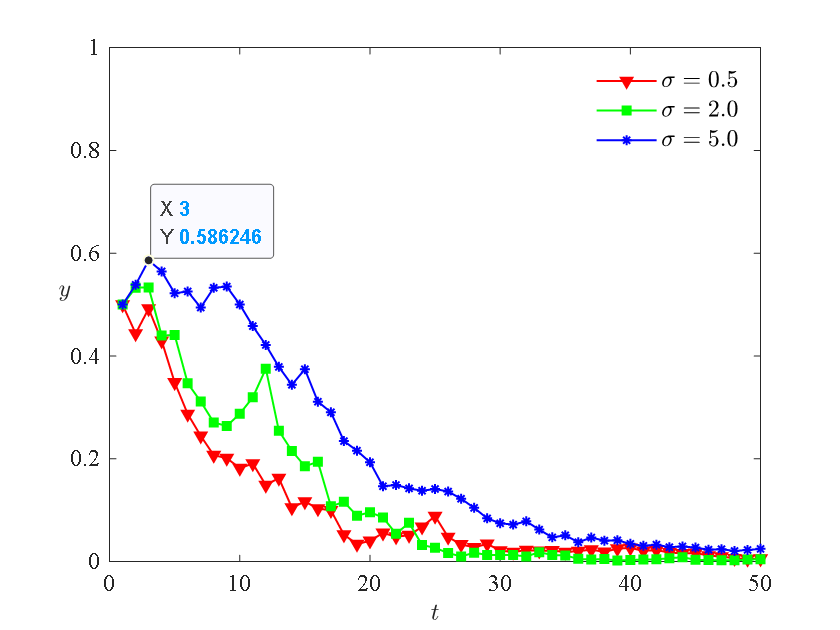
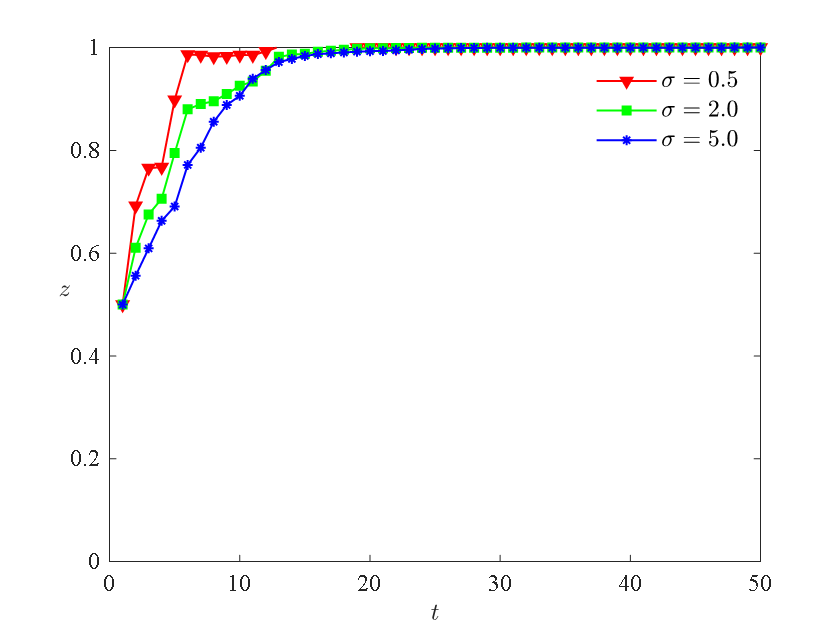
To explore the system's evolutionary process under different random disturbance intensities, we make \( σ=0.5,2,5 \) and three scenarios are simulated for analysis, and the system's evolutionary paths are shown in Figures 4-6:

From Figures 4-6, it can be observed that farmers, logistics enterprises, and government regulatory departments all exhibit varying degrees of fluctuations under the influence of random disturbance factors during the evolutionary process. Ultimately, they evolve to the same strategy set (pre-cooling, cold chain transportation, strict regulation) as in the absence of random disturbance factors. This indicates that, although the final stable result remains unchanged under the influence of internal factors such as risk perception and external factors such as government policies, it does affect the process and speed of evolution to stability.

Comparing Figures 4 and 5: (1) With the increase of random disturbance factors, the predictive ability of entities for environmental changes gradually decreases, leading to an increase in the amplitude of fluctuations and a slowdown in the speed of evolution to stability. As the game progresses, farmers and logistics enterprises gradually adapt to the uncertain environment, reducing the impact of disturbance factors, and the proportion of individuals choosing the final strategy (normal processing, normal transportation) decreases to 0. (2) Farmers' fluctuations are larger, rising to 0.7723 at \( σ=5 \) , which is greater than the maximum rise of 0.5862 for logistics enterprises. This indicates that farmers in the cold chain transportation system are more susceptible to random factors (3). Additionally, farmers evolve to stability faster than logistics enterprises. For example, at \( σ=5 \) , farmers tend to stabilize at \( t=35 \) , while logistics enterprises remain unstable at \( t=50 \) . This suggests that farmers are more inclined to invest in the cold chain.

From Figure 6, it can be observed that government regulatory departments are more inclined to choose loose regulation as a stable policy, and the greater the random disturbance intensity, the faster government regulatory departments evolve to a stable strategy. This is because increasing random disturbance factors represent uncertainty in the environment for government regulatory departments. The increase in uncertainty reduces their predictive ability for environmental changes, limiting decision-making and slowing down their evolution to a stable strategy.

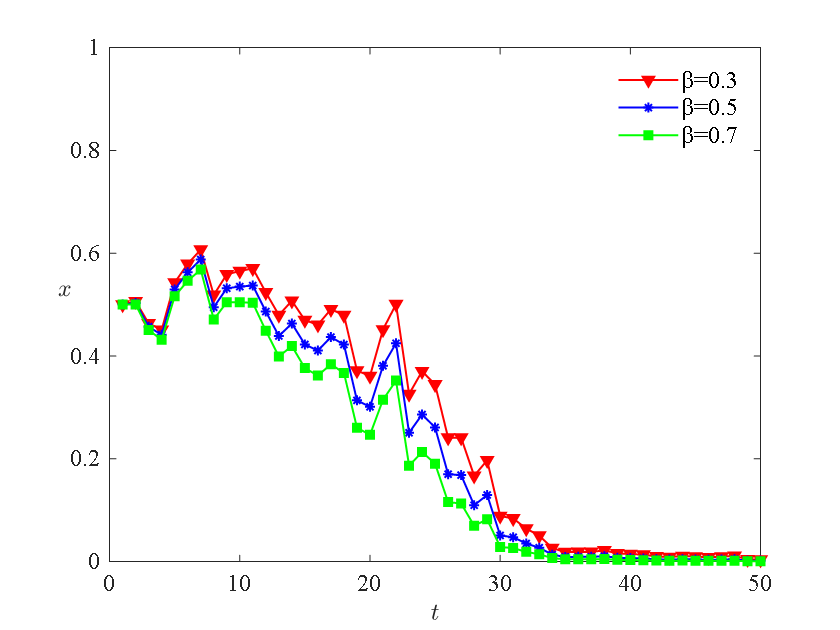
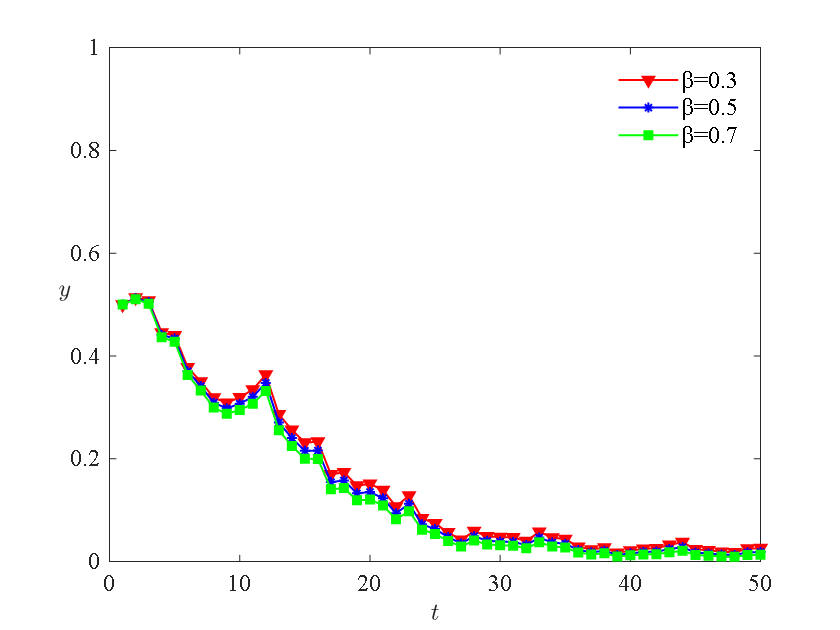
4.3. Impact of Loss Transmission Coefficient on the Evolutionary Process

From Figures 7 and 8, it can be observed that the speed of evolution to a stable strategy for both farmers and logistics enterprises increases with the increase of the loss transmission coefficient \( β \) . Additionally, farmers are more sensitive to the impact of the loss transmission coefficient compared to logistics enterprises. This is because an increase in \( β \) means that the penalty for not choosing cold chain processing for farmers and not choosing cold chain transportation for logistics enterprises increases, prompting them to be more inclined to choose to invest in the cold chain to avoid the high penalties imposed by strict government regulation.

4.4. Impact of Expenditure Proportion Coefficient for Cold Chain Upgrade on the Evolutionary Process

From Figures 9 and 10, it can be observed that the speed of evolution to a stable strategy increases with the increase of the expenditure proportion coefficient for cold chain upgrade \( α \) . Additionally, farmers are more sensitive to the impact of \( α \) compared to logistics enterprises. This is because an increase in \( α \) means that the cost for farmers and logistics enterprises not choosing cold chain processing and transportation, respectively, increases. This prompts them to be more inclined to choose to invest in the cold chain to avoid the high costs associated with strict government regulation.

5. Conclusion

This paper addresses the issue of various random disturbance factors in the cold chain transportation supply chain. A \( It\hat{o} \) stochastic attack-defense evolutionary game model is established using stochastic differential equations to analyze the impact of various random disturbance factors such as disturbance intensity and strategy changes on the evolution of attack-defense strategy selection. The stability of the strategy selection state is analyzed based on the stability criterion for stochastic differential equations. However, this study has certain limitations. For instance, the constructed model does not consider the complexity of social network structures, and the unavailability and complexity of certain real-world data pose significant challenges to further in-depth research. These aspects need attention and resolution in future studies.