1. Introduction

Using machine learning to predict house prices is very popular today. With the well development of economic, people prefer to pay more attention to housing. As home prices are gradually falling, people's interest in purchasing a home has greatly increase. Although people have better economic conditions, people can’t not make choices on buying houses easily. Whether buying a house is a necessity or an investment? Most people will buy a house or sell a house at the end [1]. This requires people to make accurate predictions about house prices. A common idea of buying a house is not only the basic need to live, but also the hope that the price of the house will go up so that people can profit from it, this idea is especially prominent among the houses buyers who buy houses for investment purposes. The study of property values will also help the Government in its urban arrangements [2]. House prices change every day [3]. Therefore, in addition to analyze by themselves, analyzing it through a machine learning model is very common. Although there are various kinds of algorithms such as Decision Tree (DT) models, they are mostly scattered. It is important to integrate some of the models to provide an intuitive feel for the performance of various predictive models. The integration and comparison of various types of models will provide people with a convenient way to predict the prices.

With the development of machine learning, it is becoming common to use machine learning to predict house prices. Real estate market research based on machine learning is mainly oriented towards house price indices, trend forecasting and house price valuation [4]. The rise of big data and high-performance computing technologies can help people accurately predict house prices through advanced machine learning algorithms [5]. Many factors that influence property prices such as location, the size of the room and height are more linearly related to the price of a home. Using linear regression (LR) to predict house prices can yield good results. Then most of the studies started to use Random Forest (RF) models, which have high accuracy in predicting house prices. The datasets utilized in this paper are classical machine learning cases from Kaggle about Boston Home Price Prediction. This dataset utilizes DT and RF models for prediction and RF had better performance. Moreover, As the study progressed, researchers began to use ensemble learning refers the Extreme Gradient Boosting (XGBoost) had better performance in the realm of predicting house prices [6]. More attention has been paid to how to correctly predict house prices and profit from them, but there has been a lack of attention to what people are buying houses for. Similarly, after correctly predicting house prices, will people's willingness to buy increase and will their aim change from buying a house to live in to buying a house as an investment? This lacks a certain amount of study. Recent years have seen a growth in interest in theories of house price expectations which are characterized by some form of extrapolation of recent growth [7]. The real estate market industry is an extremely large market. Real estate investment has been the main driver of China's economic growth over the past decade. Private housing investment accounted for 15.1 %of total urban investment in 2008 and 13.2 % of total urban investment in 2009 [8]. Based on machine learning, it is very effective to use it for house price prediction for investment because its excellent performance.

This paper utilizes a classic dataset from Kaggle, which contains a lot of factors influencing the price of houses in Boston. The research framework includes data collection, model training, testing, and performance evaluation. The methodologies employed in this study include RF, DT, Gradient Boosting (GB), XGBoost, and LR. The study identifies two main factors significantly affecting house prices in the dataset: the distribution of room counts (RM), with outliers representing properties with unusual room numbers, and the percentage of the lower-status population (LSTAT). Among the models, RF demonstrated strong performance, achieving an accuracy of 89.89%, reaffirming its effectiveness in predicting house prices. However, the paper also found that the GB and XGBoost models outperformed RF, indicating their superior predictive capabilities in this context. This underscores the importance of selecting appropriate models, such as GB and XGBoost, for accurate house price prediction. Given the rising demand for homes in an era of fluctuating prices, machine learning has become an indispensable tool for predicting house prices accurately, whether for investment, policy-making, or individual decision-making.

2. Methodology

2.1. Dataset Description and Preprocessing

The article utilizes the classic dataset from Kaggle called ‘Boston Housing Price Prediction’ [8]. The dataset contains a variety of factors that influence home prices in Boston. In this paper the author refines the model based on this dataset and add new models to explore models with good performance for predicting house prices. The dataset contains 506 cases, involving 7,084 pieces of data. It includes factors affecting house prices such as per capita crime rate by town (CRIM) and Median value of owner-occupied homes in $1000s (target variable) (MEDV). The framework included collecting data, planning, training, testing, and running the different models. The dataset has no any missing values, so the author can employ the data for learning.

2.2. Proposed Approach

The Figure 1 illustrates the research process. The dataset provides two methods to learn RF, DT. In this paper, thesis add the GB, XGBoost to this case, effectively draw conclusions from the dataset through machine learning, and summarize the four models to provide a model with excellent performance. RF, DT, GB and XGBoost constitute the methodologies.

Figure 1: The process of the research.

2.2.1. Random Forest (RF)

RF contains various independent decision trees. The final prediction is created by aggregating the predictions of all the decision trees. The result is calculated by voting or weighted average of the predictions of all the decision trees. RF is very effective in handling with multiple samples and many features and is also very advantageous in dealing with nonlinear problems. In addition, RF also focuses on reducing variance. The Bagging method has no dependency between the base learners during the training process, allowing for parallel training. RF can quickly deal with the overfitting problem. In terms of predicting house prices, RF can be computed in parallel to process data more efficiently; RF can effectively handle complex relationships and deal with missing values to effectively assess the importance of features; more importantly, RF is resistant to overfitting and can be adapted to various types of data. In this study, RF is provided by the dataset and achieved good results.

2.2.2. Decision Tree (DT)

DT has two types which is classification trees and regression trees It is also particularly suitable for integrated learning. Building a decision tree is divided into three parts: select features, decision tree generation, and decision tree pruning.

DT is also known as judgment tree, and it embodies decision rules and classification results based on a tree-shaped data structure. DT is an inductive learning algorithm that transforms chaotic-looking known instances into a tree model to predict unknown instances. DT can clearly represent the decision-making process of data and construct a tree structure by splitting the features in house price prediction, so the prediction process is intuitive. Meanwhile, DT has low requirements for data preprocessing and can handle missing values. Moreover, DT can effectively deal with nonlinear relationships, and the prediction speed is fast, which is suitable for small-scale datasets. In this study, DT was provided by the dataset and achieved reliable results.

2.2.3. Gradient Boosting (GB)

The GB algorithm is an integrated learning method. The learning program kept fitting the new models to provide estimates of the response variable which are more accuracy. The principle is to construct a new base learner that maximizes the negative gradient of the loss function associated with the entire ensemble [9]. The basic idea of GB method is to create multiple weak learners in succession. In terms of predicting house prices, GB has a strong generalization ability to effectively reduce overfitting, and it can effectively handle missing values and reduce the complexity of data preprocessing. Despite the slow training process, GB has better predictability than other models. The application of this model in this study is intended to be compared with RF and DT.

2.2.4. Extreme Gradient Boosting (XGBoost)

XGBoost is a machine learning system that can be used for remote enhancement. GB is mainly used for regression and classification tasks. The system has made a significant impact in machine learning and data mining challenges and is widely recognized [10]. Moreover, In XGBoost, the trees are constructed in parallel, not sequentially as in Gradient Boosted Decision Trees (GBDT). GB is based on a gradient boosting framework to optimize the predictive power by constructing decision trees step by step in predicting house prices XGBoost will be more accurate, flexible and effective in dealing with missing data values, one can optimize the tuning parameter based on the actual problem, what's more, it supports parallel computation, which significantly improves the training speed. XGBoost provides feature importance evaluation and supports parallel computation and powerful regularization to prevent overfitting. The application of this model in this study is intended to be compared with RF and DT.

3. Result and Discussion

In this study, this paper visualizes the data and creates heatmap to visualize the correlations between various variables for preliminary analysis. The following Figure 2 and Figure 3 visualize the factors which provides insights into the variability of housing features across different areas of Boston.

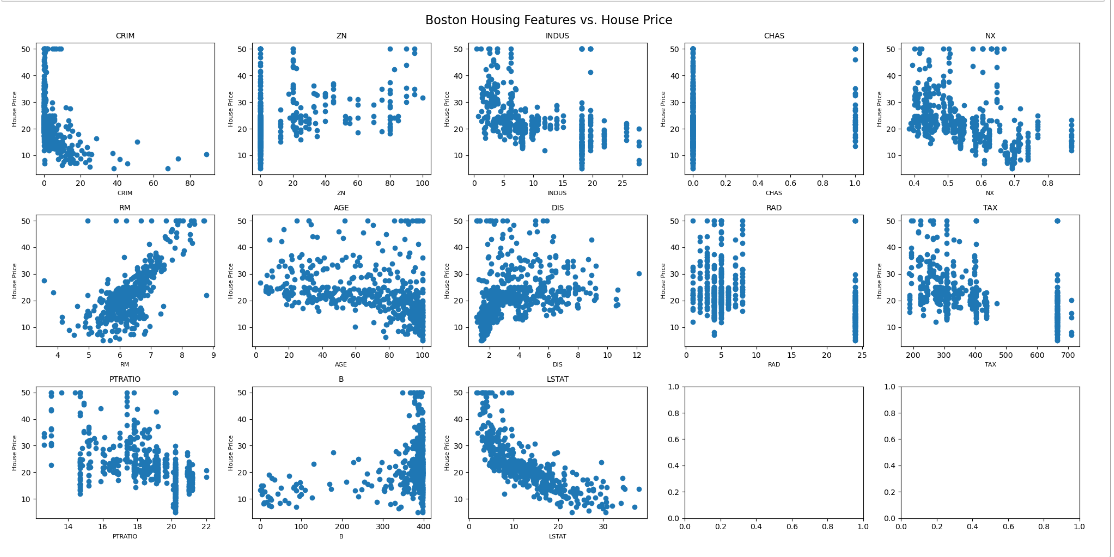
Figure 2: Boston Housing Features vs House Price.

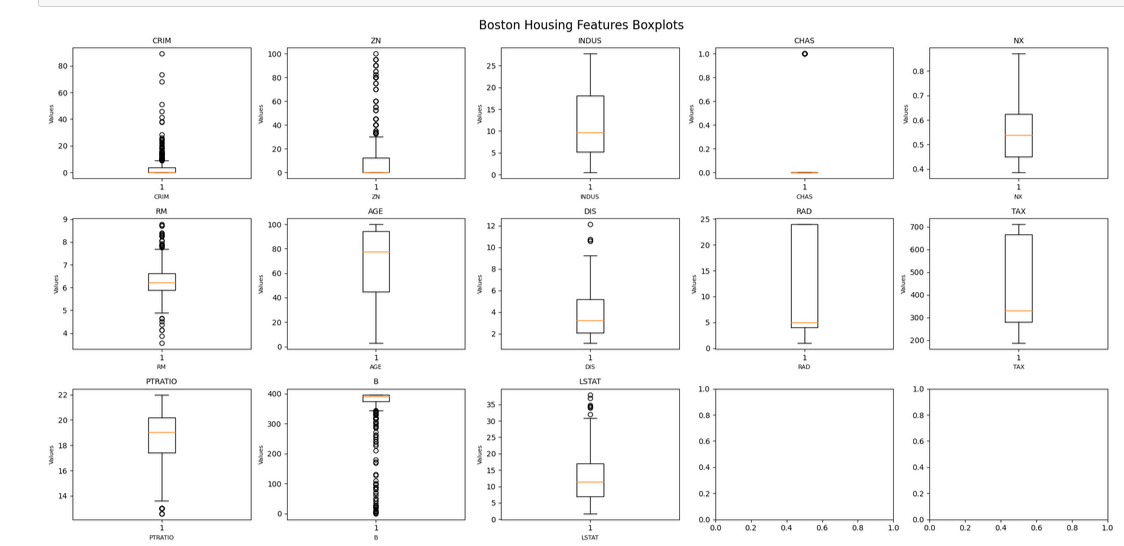
Figure 3: Boston Housing Features Boxplots.

Furthermore, Figure 4 exhibits a heatmap to visualize the correlations between various variables. This will help to find out what kind of correlation various factors have with house prices. The main factors affecting house prices in this dataset are RM and LSTAT.

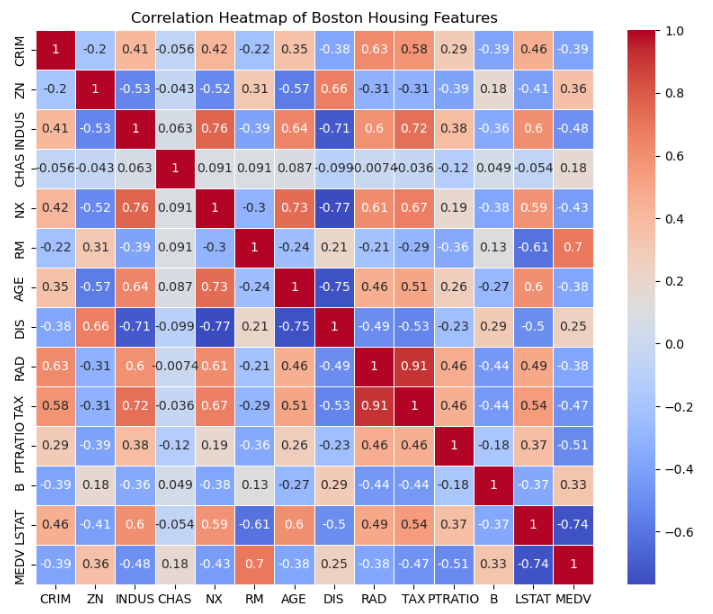
Figure 4: Correlation Heatmap of Boston Housing Features.

The dataset provides bar charts of the distribution of median housing prices in different Boston neighborhoods, which helps to understand the range and distribution of housing prices in Figure 5. The number of very high-priced properties is small. Home prices range from $5,000 to $50,000. Home prices vary widely but are concentrated between $10,000 and $23,000.

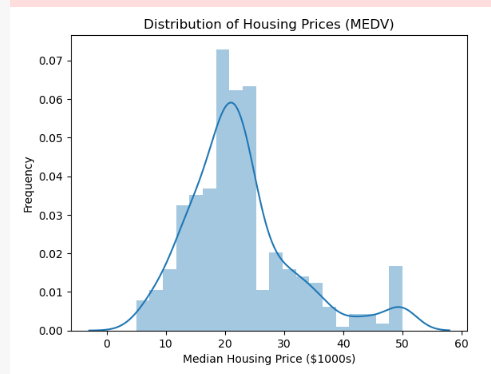
Figure 5: Distribution of Housing Prices (MEDV).

The models all reflect higher accuracy, as well as lower Mean Squared Error (MSE), Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) which can visualize the magnitude of the error in the prediction model. Therefore, it is useful to predict based on machine learning. GB algorithm has better performance when compared the accuracy to all the other algorithms in house price predictions. The Table 1 shows the performance, and the yellow markings represent the most effective. Each model achieves an accuracy of 80% or more The GB model and the XGB model have a particularly good performance, the GB model has an accuracy of 89.99 % with an MSE of 7.79. while the XGB model has an accuracy of 90.20 % with an MSE of 8.40. The two models are superior to RF and DT, the accuracy of RF model is 89.89 % and MSE is 9.12. whereas the accuracy of DT model is 83.15 % and MSE is 22.21, The MSE of DT is significantly higher than that of the other models. The errors for each model are small and very similar. Virtually every model has had good results in predicting house prices.

Table 1: Performance of different algorithms.

In summary, the work uses four algorithms to process the predicted future house price data: RF, DT, GB, XGBoost. The GB and XGBoost have the highest accuracy. This study integrates and compares different algorithms to make it easier for people to choose the right model for the algorithm. More importantly, it greatly improves people's understanding of purchasing a house as well as to help them increase the possibility of making profits.

4. Conclusion

With the growing interest in home buying, it will be useful to predict the house price based on machine learning. This paper examines four algorithms includes RF, DT, GB, and XGBoost and finds that GB and XGBoost outperform the others, delivering the highest accuracy and lowest error rates. The strength of the GB algorithm lies in its ability to capture complex nonlinear relationships, making it particularly well-suited for handling the multifaceted elements that influence house prices, such as location, size, and nearby amenities. While the study demonstrates the effectiveness of GB and XGBoost in house price prediction, it is limited by the dataset, which does not account for buyers' motivations, such as purchasing for immediate needs versus investment. These psychological factors, although crucial, require more extensive data to fully capture. In future research, exploring how machine learning models might influence or predict changes in buyers' willingness to purchase. Explore whether the willingness to buy a house increases with correctly predicted house prices which could provide further insights into housing market behavior.