1. Introduction

The real estate market has long been a subject of interest and study due to its significant impact on the economy and people’s lives. In recent years, housing prices have experienced dramatic fluctuations, raising concerns among policymakers, investors, and the general public. These fluctuations are not confined to local markets but are often part of a global phenomenon, as demonstrated by the housing market crises in various countries [1]. The complexity of the housing market, with its myriad of interacting variables, necessitates a robust analytical framework to understand and predict its behavior [2]. This paper aims to explore the intricate relationship between housing prices and game theory, providing insights into the strategic interactions among various market participants.

Housing prices, influenced by a multitude of factors such as supply and demand, government policies, and economic conditions, play a crucial role in shaping the real estate market [3]. The rise and fall of housing prices can have far-reaching consequences for both individuals and the overall economy. For instance, the housing bubble and subsequent crash of the late 2000s had profound implications for financial stability and economic growth [4]. On one hand, soaring housing prices may lead to increased wealth for homeowners, while on the other hand, they can create affordability issues for potential buyers and exacerbate social inequality [5, 6].

Game theory, a branch of mathematics that deals with the analysis of strategic interactions, offers a valuable framework for understanding the complex dynamics of the real estate market [7]. By modeling the behavior of market participants, such as developers, investors, and policymakers, as players in a game, a deeper understanding of the factors driving housing prices and the potential outcomes of various strategies can be seen. The application of game theory to real estate markets has been explored in various contexts, including the analysis of land use competition and the impact of regulatory policies on market outcomes [8, 9].

The interplay between housing prices and game theory is particularly relevant in the context of market bubbles and crashes [4]. The speculative nature of real estate investments often leads to non-cooperative behavior among investors, with each trying to maximize their returns without considering the collective impact on the market. This paper will examine how the principles of game theory can be used to predict and mitigate the risks associated with such speculative behavior.

This paper borrows from a brief overview of the key concepts in game theory and their relevance to the real estate market, drawing on the foundational work by von Neumann and Morgenstern [10]. Next, the paper focus on the discussion of the factors influencing housing prices and examine how game theory can be applied to analyze these factors, building on the contributions of economic scholars. Furthermore, there is the investigation about the role of information asymmetry in the housing market and how it affects the strategies of buyers and sellers.

The empirical section of the paper will present a case study of a specific real estate market to illustrate the application of game theory in practice. By discussing three hypothetical games between realtors and realtors, between realtors and government, and between realtors and consumers will identify patterns and strategic interactions among market participants. The case study will highlight the importance of considering both the rational and irrational aspects of market behavior when applying game theory to housing markets.

Some implications of findings for policymakers and market participants will be given, offering recommendations for mitigating the negative effects of housing price volatility and promoting a more stable and equitable real estate market, in line with the suggestions put forth by Glaeser and Rode et al. [11, 12]. The need for a multi-faceted approach will be argued that combines traditional economic analysis with insights from game theory and behavioral economics to inform more effective housing policies.

By integrating game theory into the analysis of housing market dynamics, this paper aims to contribute to the existing body of knowledge and provide practical insights that can inform more strategic decision-making by all stakeholders involved in the real estate market.

2. Methods

2.1. Data Source

The data used in this paper is not actual data, but more of a theoretical analysis with equations of relevant variables. It is actually based on the discussion of the relationship of the variables in the three cases mentioned above.

2.2. Indicator Selection and Description

In discussing the game between realtors and realtors, this paper draws on the Bertrand model, a classic model in economics used to describe price competition in an oligopolistic market. This model assumes that several oligopolistic players in a market produce homogeneous products and that consumers are very price sensitive and will buy the lowest priced product. Several important indicators are \( Q \) , \( P \) , \( C \) , \( Z \) , which represents the output, product price, cost and profit of the two firms respectively.

In discussing the game between realtors and government, this paper introduces two additional indicators \( N \) and \( E \) , which represents the number of houses and the consumption of public resources respectively.

2.3. Method Introduction

In the Bertrand model, the following key assumptions hold: First, Homogeneous products: all realtors produce exactly the same products, which consumers perceive as substitutable for each other. Second, Price competition: realtors compete with each other by setting prices, not by changing output. Third, Perfect information: consumers know the prices of all realtors and can switch to the lowest priced realtor at no cost. Fourth, Zero marginal cost: the cost of producing an additional unit of a good is zero, which means that realtors can produce the good without limitation.

The equilibrium outcome of the Bertrand model usually looks like this: In a Bertrand equilibrium, all realtors end up setting the same price, which is equal to their marginal cost. This is because if one vendor sets a price higher than marginal cost, the other realtors can take all the market share by lowering their prices slightly. Therefore, the end result is a price similar to that of a perfectly competitive market, even though there are only a few realtors in the market

The above is a background theory, and this paper will discuss different situations by comparing the profits to get the dominant strategies for different people, and during the discussion, it will involve derivation and maximization calculations, and will be illustrated with some tables.

3. Results and Discussion

3.1. Realtors and Realtors

Assuming that there are only two realtors, A and B, in the secondary real estate market; and their output, product price, cost and profit are \( {Q_{A}} \) , \( {Q_{B}} \) , \( {P_{A}} \) , \( {P_{B}} \) , \( {C_{A}} \) , \( {C_{B}} \) , \( {Z_{A}} \) , \( {Z_{B}} \) respectively. In addition to this, the products of the two realtors are indistinguishable; which means they have the same products. The production capacity of each realtor can satisfy the demand of the whole market. The two realtors play the game with the price as the guiding signal. The price is the only variable of the output, so \( Q \) is related to \( {P_{A}} \) and \( {P_{B}} \) , which means \( Q=({P_{A}}, {P_{B}}) \) . By the way, from the Bertrand model, the following equation can be obtained.

\( Q=l-m{P_{A}}+n{P_{B}} \) (1)

In the above formula, \( l \) , \( m \) and \( n \) are constants representing the parameters of the demand function and \( 2m \gt n \) .

With the above assumptions, the profit function of realtor A and realtor B can be obtained as follows

\( {Z_{A}}={Z_{A}}({P_{A}},{P_{B}},{C_{A}})={P_{A}}{Q_{A}}-{C_{A}}{Q_{A}}=({P_{A}}-{C_{A}})(l-m{P_{A}}+n{P_{B}}) \) (2)

\( {Z_{B}}={Z_{B}}({P_{A}},{P_{B}},{C_{B}})={P_{B}}{Q_{B}}-{C_{B}}{Q_{B}}=({P_{B}}-{C_{B}})(l-m{P_{A}}+n{P_{B}}) \) (3)

When the profits of realtor A and realtor B are maximized, the derivative of the two equations is 0.

\( {Z_{A}}{({P_{A}})^{ \prime }}=l+n{P_{B}}+m{C_{A}}-2m{P_{A}}=0 \) (4)

\( {Z_{B}}{({P_{B}})^{ \prime }}=l+n{P_{A}}+m{C_{B}}-2m{P_{B}}=0 \) (5)

Joining the above two equations gives

\( {P_{A}}=\frac{(2lm+nl+nm{C_{B}}+2{m^{2}}{C_{A}})}{(4{m^{2}}-{n^{2}})} \) (6)

\( {P_{B}}=\frac{(2lm+nl+nm{C_{A}}+2{m^{2}}{C_{B}})}{(4{m^{2}}-{n^{2}})} \) (7)

This analysis can be obtained, when \( {P_{A}} \gt {P_{B}} \) , consumers will only buy products of realtor B, and will not buy products of realtor A, at this time \( {C_{A}} \gt {C_{B}} \) . For the same reason, when \( {P_{B}} \gt {P_{A}} \) , consumers will only buy products of realtor A, and will not buy products of realtor B, at this time \( {C_{A}} \gt {C_{B}} \) . When \( {P_{A}}={P_{B}} \) , there is no difference between the products purchased by consumers from realtor A and B, at the time \( {C_{A}}={C_{B}} \) .

From the above analysis, it can be seen that the competition between the two realtors is mainly a cost competition, low-cost realtors will occupy the market, and high-cost realtors will be eliminated. In equilibrium, A and B, the two realtors will equally share the entire market. These conclusions are ideal state, which are not possibly happened in reality. No realtors can develop a real estate product to meet the requirements of the entire market, there will be certain conditions of the limitations (such as production capacity, technology, etc.), purely by way of price cuts cannot be achieved by squeezing out the rivals of the purpose.

For further analytical discussion, it is necessary to use the modified Bertrand model. Assuming that the maximum production capacity of both realtor A and realtor B is \( k \) , the marginal cost is \( W \) and the market demand function is \( Q=D(P) \) . Then the demand function faced by realtor \( i \) can be expressed as: \( min⁡[D({P_{i}})-k,k] \) . When \( {P_{A}} \gt {P_{B}} \) , based on the assumptions of the above model, if realtor A pricing is \( {P_{A}}=W \) . then when \( k \lt D(W) \) . it will not be able to satisfy the demand of the whole market. At this time there will be a portion of consumers turn to buy the products of realtor B. In this way, realtor B has the demand of the remaining market and can price above marginal cost. Similarly, when any realtors determine their price higher than the marginal cost, if another realtor lowers its price to compete, the production capacity constraint does not allow the realtor to capture all of the market. Thus, in general, no any real estate company will take the strategy of low-price competition.

As can be seen from the above analysis, the consequences of a price war can be a lose-lose situation for both realtors. However, the real estate companies in reality are rational, and their best choice is to move from confrontation to cooperation: Restriction of production to increase prices and jointly manipulate the market.

Now consider the specific data of the Bertrand model of the form: so that \( l=4 \) , \( m=1 \) , \( n=2 \) , then the following equation is given by (1),

\( {Q_{A}}=4-2{P_{A}}+{P_{B}} \) (8)

\( {Q_{B}}=4-2{P_{B}}+{P_{A}} \) (9)

Let the cost \( {C_{A}}={C_{B}}=W=1 \) , then the profit of two realtors are,

\( {Z_{A}}=({P_{A}}-1)(4-2{P_{A}}+{P_{B}}) \) (10)

\( {Z_{A}}=({P_{A}}-1)(4-2{P_{A}}+{P_{B}}) \) (11)

Through the same computational process as in the previous section, when equilibrium has been reached, it is obtained that,

\( \begin{cases} \begin{array}{c} {P_{A}}={P_{B}}=2 \\ {Q_{A}}={Q_{B}}=2 \\ {Z_{A}}={Z_{B}}=2 \end{array} \end{cases} \) (12)

Now it appears that the two products are produced in a monopoly industry, then the total profit is,

\( Z={Z_{A}}+{Z_{B}}=({P_{A}}-1)(4-2{P_{A}}+{P_{B}})+({P_{B}}-1)(4-2{P_{A}}+{P_{B}}) \) (13)

The first order derivative is,

\( {Z({P_{A}})^{ \prime }}=5-4{P_{A}}+2{P_{B}} \) (14)

\( {Z({P_{B}})^{ \prime }}=5-4{P_{B}}+2{P_{A}} \) (15)

Let both equations be 0 and the condition of profit maximization when the two firms cooperate is,

\( \begin{cases} \begin{array}{c} {{P_{A}}^{ \prime }}={{P_{B}}^{ \prime }}=\frac{5}{2} \\ {{Q_{A}}^{ \prime }}={{Q_{B}}^{ \prime }}=\frac{3}{2} \\ {{Z_{A}}^{ \prime }}={{Z_{B}}^{ \prime }}=\frac{9}{4} \end{array} \end{cases} \) (16)

Obviously, \( {{Z_{A}}^{ \prime }} \gt {Z_{A}} \) and \( {{Z_{B}}^{ \prime }} \gt {Z_{B}} \) .

Therefore, collaboration is profitable for realtor A and realtor B, but if one realtor secretly betrays the cooperation contract to produce \( Q \) instead of \( {Q^{ \prime }} \) , the price yet remains \( {P^{ \prime }}=\frac{5}{2} \) , then the profit of that defaulting realtor is,

\( Z=2*(\frac{5}{2}-1)=3 \gt \frac{9}{4} \) (17)

At this time, the results of the two realtors will fall into the ‘prisoner dilemma’. Table 1 is the result between the two real estate development enterprises.

Table 1: The result of the game(if one realtor chooses to betray)

By method of drawing a line, it can be seen that the final choice of the two realtors is the result of non-cooperation, which is also consistent with the reality of China's real estate. Some enter the real estate industry is to take advantage of the real estate market boom to obtain current profits. And they did not take the long-term profits into consideration, so this alliance is deeded to fail. Sensible real estate companies in the pursuit of profit maximization realize the fact that in the process of introducing the time dimension of the repeated game, their own behavior have considerable influence on their competitors. Since the result of price reduction by either realtor inevitably reduces his own profits, no one will sell at a reduced price. Even though the real estate companies are completely independent, the equilibrium result is as if they had entered into a monopoly agreement. Therefore, price collusion between real estate companies would be a more rational strategic choice.

3.2. Realtors and Government

Assuming that the profit function of realtors is,

\( {Z_{R}}=N(P-C)-E \) (18)

In the above formula, \( {Z_{R}} \) is the profit earned by the realtor, \( N \) is the number of houses sold, \( P \) is the price of the houses sold, \( C \) is the cost of the houses, and \( E \) is the expenditure on public goods.

The objective function of the local government can be expressed as follows,

\( {Z_{G}}=N(T-{P_{C}})-({E_{D}}-E) \) (19)

In the above formula, \( {Z_{G}} \) is the revenue gained by the local government in the real estate development project, \( T \) is the tax revenue of per house, \( {P_{C}} \) is the additional welfare expenditure of per house by the local government, such as the additional pension and education subsidies for the buyers, and \( {E_{D}} \) is the negative effect of social and environmental deterioration brought by the development.

Using \( e \) to denote the average social profit of capital, it follows that for the realtors, they are willing to develop as long as \( {Z_{R}} \gt e \) , and for the government, the it is willing to take out land for development as long as \( {Z_{G}} \gt e \) . The model between the realtors and government at the level of commodity housing supply is a dynamic game model with incomplete information, as shown in Figure 1.

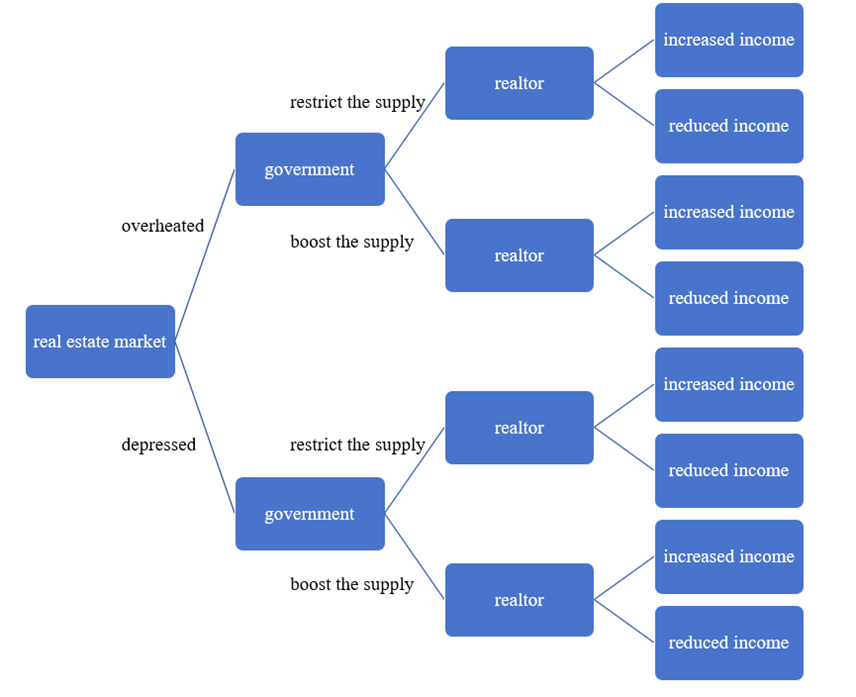
Figure 1: The game model between realtors and the government

3.3. Realtors and Consumers

In terms of housing sales, the game between realtors and consumers is the closest and most concerned in the real estate market. Consumers’ expectation is not that the lower the price of a house the better. As the standard of living improves, consumers will not blindly wait for the price of a house to drop indefinitely, they will analyze the current price of a house and wait until the price of a house returns to a price they can accept in their own mind and make a move immediately. Therefore, it is not that there is no demand in the market at this stage, but that they are waiting for prices to return. Assuming that there are only two separate players in the entire real estate market, realtor A and consumer B, the process of their game can be expressed simply in the following table 2.

Table 2: The game process between realtors and consumers

From the above game process, it is can be seen that when the realtor maintains the price of house unchanged, consumers would take a wait-and-see attitude, and the atmosphere of the entire market will become undesirable, people's expectations of the transaction to the minimum, the loss of the market will eventually be manifested in the transaction of two sides. However, when the realtor began to reduce prices, which meet the psychological expectations of people in the market, this time the market gradually with the warmth, and the both sides can profit, achieving a win-win situation in this stage.

Therefore, the end result of the game between rational realtors and consumers should be price reductions and enter the market. This also depends on the magnitude of the price cuts and consumer expectations of price reductions whether in line with the value.

4. Conclusion

From a long-term perspective, real estate companies should avoid large-scale price wars and ensure the quality of each development link, thus making their products more competitive.

The government in creating a good environment for the real estate market, should be open access to information and improve the authenticity of information. It can also change the weak position of consumers in the game by improving the supervision mechanism, the establishment of real estate information consulting agencies and objective and effective evaluation standards.

As for consumers, from the point of view of repeated games, consumers should make comparisons when purchasing houses. It is also a good choice for consumers to learn some knowledge about credit consumption and investment and finance management, control their personal debts and learn to consume moderately and reasonably.