1. Introduction

Solana (SOL) is a high-performance blockchain designed to provide decentralized applications (dApps) and cryptocurrencies with fast, secure, and scalable solutions. Launched in 2020, Solana has garnered significant attention for its innovative architecture, which leverages proof-of-history (PoH) in conjunction with proof-of-stake (PoS), a combination that allows it to process over 50,000 transactions per second (TPS) without compromising decentralization or security [1,2]. This technical edge positions Solana as one of the leading platforms in the blockchain space, offering significant advantages in scalability compared to Ethereum, which is currently grappling with scalability challenges. Solana's performance places it in a favorable position within the blockchain “trilemma”, where it maintains a balance between decentralization, security, and scalability, outperforming many of its competitors in the process.

As of late 2024, Solana’s market capitalization stands at approximately $12 billion, placing it among the top 10 cryptocurrencies globally. Despite the volatility in the crypto markets, Solana has maintained its position as a promising alternative to Bitcoin (BTC) and Ethereum (ETH), drawing significant developer interest and partnerships across DeFi, NFTs, and gaming sectors. Solana’s robust ecosystem continues to grow, making it a crucial asset for investors and blockchain enthusiasts alike.

The task of predicting Solana's price is complex and multifaceted, with researchers and market analysts using various methods to forecast its price trajectory. Traditional models often rely on historical price data, technical indicators, or on-chain data analysis to make predictions. In recent years, machine learning (ML) and deep learning (DL) models have become popular for predicting cryptocurrency prices, including Solana and Bitcoin. Models such as Long Short-Term Memory (LSTM) networks, recurrent neural networks (RNNs), and hybrid approaches that combine time-series forecasting with market indicators are also commonly employed to capture the volatile nature of the crypto markets [3,4].

Recent studies have explored the predictive power of hybrid models that combine market factors such as trading volume, market sentiment, and macroeconomic indicators with deep learning algorithms. For instance, LSTM-based models have been integrated with technical indicators such as moving averages and RSI (relative strength index) to improve prediction accuracy [5]. Similarly, models incorporating fundamental factors like Bitcoin’s price movements and halving events have been shown to provide better results in forecasting cryptocurrency prices [4]. However, there have been very few hybrid studies specifically focused on Solana, despite its rapid rise as a major cryptocurrency. Additionally, limited research has explored the use of data decomposition techniques to break down cryptocurrency price data into different frequency components, which could enhance the performance of machine learning models.

This paper presents an advanced approach to Solana price prediction using a Hybrid Data Decomposition-based Deep Learning Model that integrates multiple market factors, including Solana’s trading volume, Bitcoin price, and market trends. By combining Variational Mode Decomposition (VMD) to decompose the price data into intrinsic components and leveraging LSTM for time-series forecasting, the model captures both short-term fluctuations and long-term trends. Additionally, the hybrid model integrates market factors, such as Solana’s trading volume and Bitcoin's market dynamics, offering a more comprehensive approach than traditional deep learning models.

The method accounts for the uniquely complex interactions between various market factors and historical prices of Solana, allowing for more accurate and robust predictions. The results show that this model outperforms existing benchmarks, demonstrating its superiority in forecasting Solana’s price movements in comparison to a simple LSTM model. This paper delves deeper into the design and validation of this method, its comparative performance, and the limitations that should be considered when implementing it in real-world scenarios.

2. Methodology

This research introduces a hybrid model that combines Variational Mode Decomposition (VMD) and Bidirectional Long Short-Term Memory (Bi-LSTM) networks to predict the price of Solana (SOL), a prominent cryptocurrency. In this methodology, this paper first applies VMD to decompose the historical price data of Solana into several intrinsic mode functions (IMFs), each representing different frequency components. Then, a Bi-LSTM model is utilized to predict the Solana price based on the decomposed signals. To improve the accuracy and robustness of the predictions, this study also incorporates several key market factors, including the price of Bitcoin (BTC), trading volume, and sentiment analysis from social media, all of which are known to influence the cryptocurrency market dynamics.

2.1. Variational Mode Decomposition (VMD)

Variational Mode Decomposition (VMD) is a signal processing technique that aims to decompose a complex signal into a set of intrinsic mode functions (IMFs) by minimizing the trade-off between mode separation and frequency alignment. Unlike traditional methods like Empirical Mode Decomposition (EMD), which can suffer from mode mixing, VMD provides a more robust framework for decomposing time-series data, making it ideal for capturing different frequency components in financial time-series like cryptocurrency prices [6].

The VMD algorithm works by decomposing a time-series signal into multiple sub-signals, each characterized by a distinct frequency. The primary goal is to separate the signal into intrinsic mode functions (IMFs) while preserving the temporal coherence of the original data [6]. VMD is a flexible and adaptive method that has been shown to outperform traditional methods like Empirical Mode Decomposition (EMD) in certain applications [7]. The optimization problem for VMD is formulated as follows:

\( {min_{{u_{k}}}}\sum _{k=1}^{K}(||\frac{∂}{∂t}({u_{k}}+{z_{k}})||_{2}^{2}+α||{u_{k}}||_{2}^{2} ) \) (1)

where \( {u_{k}} \) represents the k-th IMF, \( {z_{k}} \) is a shift operator, and αα is a regularization parameter. This formulation ensures that the IMFs are well separated in the frequency domain, allowing the model to extract different temporal patterns that might not be apparent from the raw price data [6]. The method's ability to adaptively extract frequency components makes it particularly useful for analyzing complex, non-stationary signals, such as financial time series [8].

The goal of using VMD is to decompose the price time series into several IMFs, focusing on those that best capture the underlying market dynamics [6]. These IMFs are then used as inputs for the subsequent deep learning model, enabling more precise modeling of market trends [9].

2.2. Market factors that correlate with Solana price

In addition to price data, the model incorporates several market factors that are influential in cryptocurrency price forecasting. These factors are selected based on their potential impact on Solana’s price, as well as their proven utility in predicting the prices of other cryptocurrencies like Bitcoin (BTC). The factors used in the model include:

• Bitcoin Price (BTC Price): As the largest cryptocurrency by market capitalization, Bitcoin's price movements significantly influence other cryptocurrencies, including Solana. The price of BTC is often seen as a barometer for the overall health of the crypto market. Bitcoin's price fluctuations can lead to corresponding movements in altcoins like Solana due to market sentiment and investor behavior [10].

• Solana Trading Volume (Sol Volume): Trading volume reflects market activity and investor interest in Solana. A surge in trading volume often signals increased market confidence, which can lead to price increases. Conversely, low trading volumes may signal weak investor interest, leading to price stagnation or declines.

• Solana Search Trend (Sol Trend): Public interest and market sentiment can be gauged through online Google search trends. The frequency of searches for Solana can provide insights into market sentiment and upcoming demand. If Solana experiences a rise in search interest, it often correlates with increased trading activity and a potential price surge.

• Bitcoin Halving Events (BTC Halving): Bitcoin halving is a pre-programmed event that occurs approximately every four years, reducing the reward for mining Bitcoin by half. Halving events historically have been associated with significant price increases for Bitcoin and, consequently, other cryptocurrencies like Solana, likely resulting in cryptocurrencies’ market cycle of 4 years [11]. This factor is important for understanding market cycles and investor psychology surrounding Bitcoin’s supply dynamics.

These market factors are integrated into our model to offer a holistic view of the driving forces behind Solana’s price movements. Both the fundamental drivers and broader market trends that influence Solana’s value can be captured by incorporating these variables.

2.3. Bidirectional Long Short-Term Memory (Bi-LSTM)

After preprocessing the data and including market factors, the information is fed into a Bidirectional Long Short-Term Memory (Bi-LSTM) network for price prediction. LSTM networks, a type of recurrent neural network (RNN), are well-suited for time series forecasting tasks due to their ability to capture temporal dependencies and long-term patterns in sequential data [12]. The bidirectional aspect of the LSTM allows the model to learn from both past and future time steps, enhancing its ability to capture the full context of the time series.

A Bi-LSTM consists of two LSTM layers—one that processes the sequence from the start to the end (forward LSTM) and another that processes it from the end to the start (backward LSTM). By combining both forward and backward information, the Bi-LSTM can learn more comprehensive temporal dependencies. This is particularly useful when predicting Solana’s price, as it allows the model to incorporate both recent and future trends in the data.

Then, the decomposed IMFs, along with additional market factors described above, are provided as inputs to the model. The Bi-LSTM model is trained to predict the next price point of Solana based on both historical price data and market factors, capturing complex temporal relationships in the data.

3. Data Collection and Processing

The dataset used for predicting Solana’s (SOL) price was carefully assembled by collecting a set of key market factors known to influence cryptocurrency price movements. The primary data sources included historical price data for Solana and Bitcoin, Google search trends related to Solana, and the Bitcoin halving index. These features were collected, processed, and aligned to ensure compatibility for use in the hybrid data decomposition model.

3.1. Solana and Bitcoin data

Historical data for Solana and Bitcoin were retrieved from the Binance API, which provides reliable and high-frequency data from one of the largest cryptocurrency exchanges. For Solana, data was available only from August 11, 2020, to the present day, with prices before this date not being available due to Solana's relatively recent introduction to the market. Therefore, the dataset spans from 2020-08-11 to 2024-11-27. Daily closing prices for both Solana and Bitcoin, and transaction volume of Solana were collected and used as the basis for the analysis.

The collected price data was then normalized using the MinMaxScaler to transform the values to a common scale, ranging from 0 to 1. This normalization step was critical in ensuring that all features were comparable in magnitude and scale, which is essential for machine learning models where feature scale can heavily impact model performance.

3.2. Google Search Trends for Solana

Google Trends data was utilized to gauge the public interest in Solana by measuring the volume of Google searches over time. However, Google Trends data is only available on a weekly basis. To match the frequency of this data with the daily price data, this study performed linear interpolation. Linear interpolation estimates daily values by assuming a straight-line change between known weekly data points. This approach is appropriate as it approximates daily fluctuations in search interest while maintaining the overall trend observed in the weekly data.

The search trend data is important because it serves as an indirect measure of public sentiment, with peaks in search interest often preceding trading surges or increased market attention. This data helps capture the sentiment-driven volatility in cryptocurrency markets, which can significantly influence prices.

3.3. Bitcoin Halving Index

The Bitcoin halving index is a crucial factor that captures the impact of Bitcoin's halving events on the broader cryptocurrency market, including Solana. This index was normalized to a scale between 0 and 1, with a value of 1 representing the halving day. As the halving date approaches, the index value increases towards 1, and once the halving event occurs, it gradually decreases towards 0. This reflects the seasonality and market dynamics influenced by Bitcoin's halving cycle, which can indirectly affect Solana's price due to their strong market correlation.

3.4. Data Alignment and Preprocessing

Once the data for Solana’s price, Bitcoin’s price, Google search trends, and the Bitcoin halving index were collected and normalized, the next step was aligning these data points by date. This alignment ensures that each time step in Solana’s price data has corresponding values for Bitcoin price, Google search trends, and the halving index. This step is crucial for maintaining the integrity of the dataset and for ensuring that the predictive model has all the necessary factors at each time step. Missing values were handled through interpolation or removal, and outliers were managed through standard statistical techniques. The resulting dataset was then split into training and testing sets, with the training set covering approximately 85% of the data and the test set comprising the remaining 15%.

After collecting and preprocessing the data, this study applied Variational Mode Decomposition (VMD) to decompose the Solana price time series into multiple intrinsic mode functions (IMFs). VMD is a signal processing technique that separates complex signals into different frequency components, allowing people to isolate high-frequency noise from low-frequency trends. This decomposition is valuable for financial time series data, which often exhibit both fast-moving fluctuations and slow-moving underlying trends.

This study decomposed the Solana price data into 10 modes. As demonstrated in the figure 1 and figure 2 below, each mode captures a different frequency or periodicity in the price movements. Higher-frequency modes (e.g., modes 8 to 10), having periodicity of less than 4 days, correspond to daily fluctuations and market noise. Lower-frequency modes (e.g., modes 1 to 3), possessing periodicity of more than 50 days, capture long-term trends that may be driven by broader economic factors or investor sentiment. The intermediate modes (e.g., modes 4 to 7), holding periodicities between 7 to 25 days, are representative of weekly or bi-weekly cycles, reflecting periodic market events that influence Solana’s price.

The VMD decomposition was performed using an advanced algorithm that effectively isolates these modes based on their frequency characteristics. This decomposition allows the model to treat each mode separately, which is advantageous for capturing different temporal aspects of the price dynamics. By separating the signal into various components, the model can better focus on the relevant patterns, improving prediction accuracy. The higher-frequency modes capture daily price fluctuations, while the lower-frequency modes highlight the more stable, long-term trends.

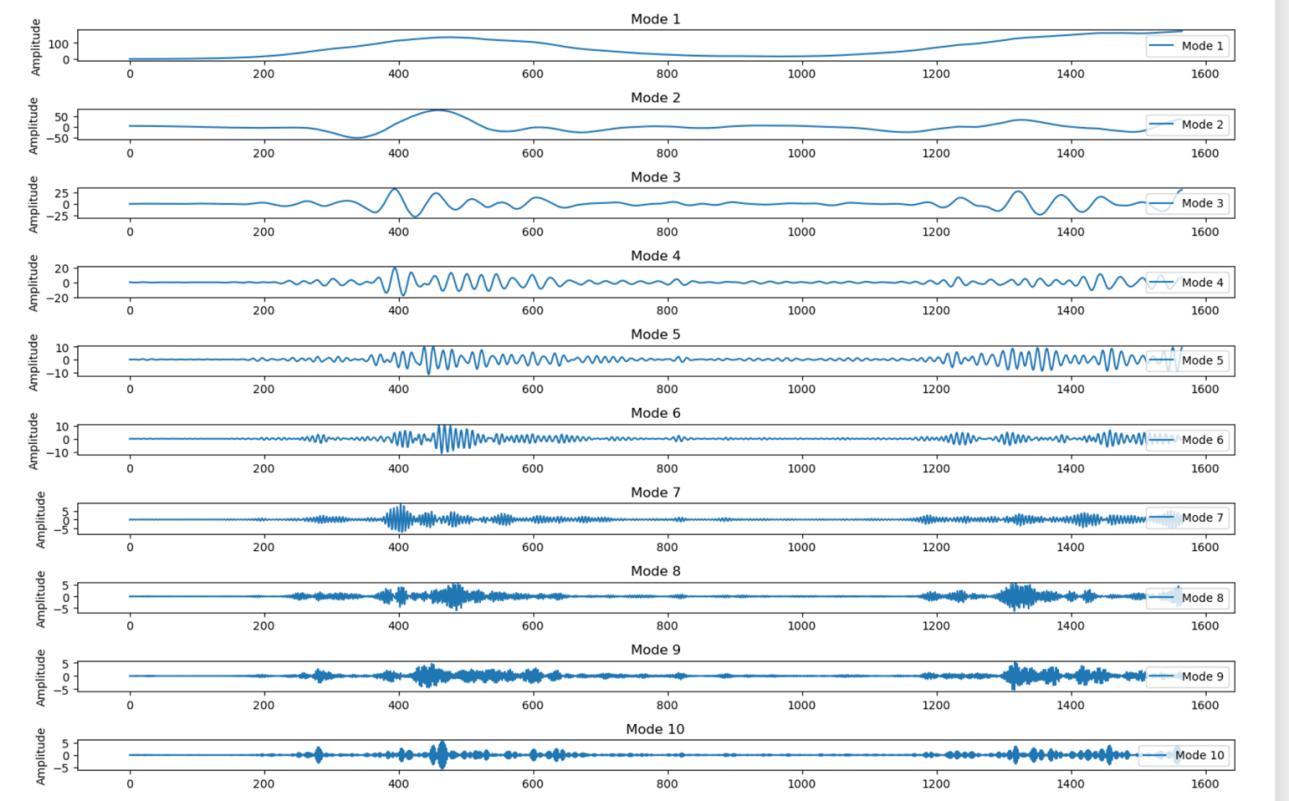
Figure 1: VMD decomposed modes of Solana price data

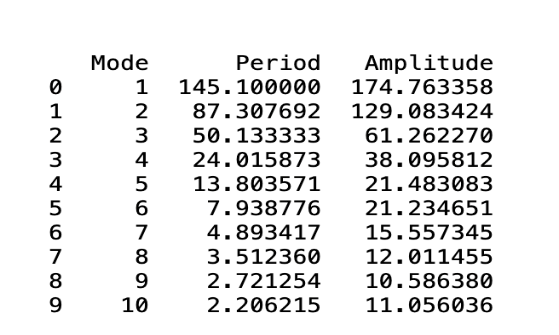
Figure 2: Different mode’s periodicity and amplitude

4. Empirical Results

The experimental results of the prediction models for Solana’s price are presented in Table 1. To evaluate the performance of the hybrid VMD-Bidirectional LSTM model, this study compared it with the benchmark LSTM model, which served as a standard deep learning model for time series forecasting. Both models were evaluated based on the following metrics: Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and R-squared (R²). These metrics help us understand the accuracy and effectiveness of the models in predicting future Solana prices.

Table 1: Benchmark model versus experimental model prediction evaluation results

The hybrid VMD-Bidirectional LSTM model outperformed the LSTM benchmark model across all evaluation metrics. The MAE for the benchmark LSTM model was 0.032, while the Hybrid VMD-Bidirectional model achieved a lower MAE of 0.0232. This indicates that, on average, the hybrid model’s predictions were closer to the actual prices than those of the benchmark model. The MSE and RMSE metrics followed a similar trend, with the hybrid VMD-Bidirectional model showing a lower MSE of 0.000776 and RMSE of 0.0279 compared to the LSTM’s 0.00166 and 0.0407, respectively. These reductions in MSE and RMSE suggest that the Hybrid model is more accurate, with fewer large errors.

The R-squared (R²) value also shows a substantial improvement, with the hybrid VMD-Bidirectional model achieving an R² of 0.915, compared to the LSTM model’s 0.819. This means that the Hybrid model explains about 91.5% of the variance in the Solana price data, whereas the LSTM model explains only 81.9%. A higher R² indicates that the hybrid VMD-Bidirectional model is better at capturing the underlying patterns in the price movement of Solana, suggesting stronger predictive power.

The comparison of the actual vs. predicted Solana price for the test set also reflects the superiority of the hybrid VMD-Bidirectional model (Figure 3), which highly coincides with the actual data trend.

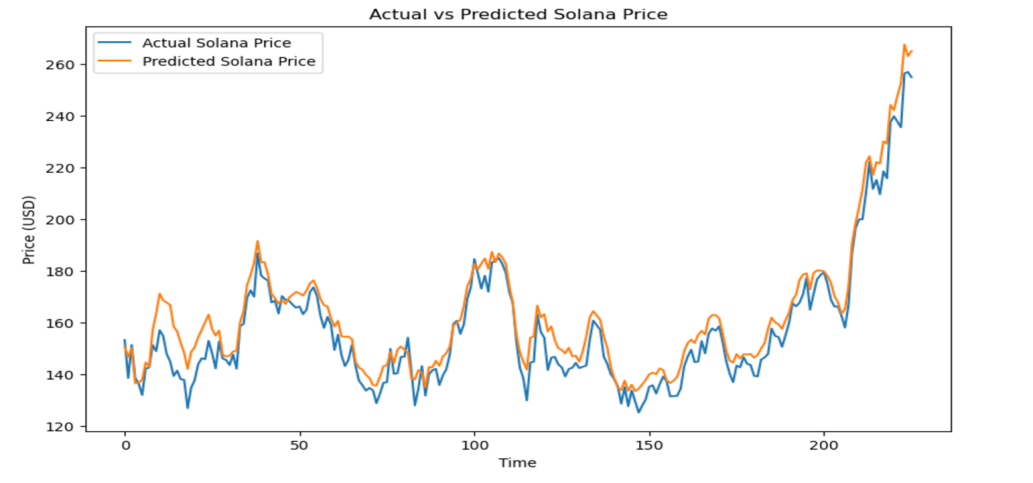
Figure 3: Actual vs. Predicted Solana price by VMD bidirectional model

This is likely a result of the decomposition process performed using Variational Mode Decomposition (VMD). By breaking down the Solana price series into multiple frequency modes, the hybrid model was able to capture both short-term and long-term trends more effectively than the traditional LSTM. The addition of Bidirectional LSTM further improved the model’s ability to leverage past and future data points, which is crucial in time series forecasting. The improved performance is a result of the hybrid approach, which incorporates both market factors and a sophisticated decomposition technique to enhance the prediction process.

Eventually, to test the practicality of the models, trading simulations were performed using daily price predictions. The models generated buy or sell signals based on price movement predictions: a "buy" signal was issued when a higher price was predicted for the next day compared to the previous day, while a "sell" signal was issued when a lower price was forecasted. In cases where no price change was anticipated, the position was held. The performance of these strategies was assessed by calculating daily returns based on the portfolio's value, considering the capital invested and the holdings in Solana.

All models started with an initial capital of $100,000. At the end of the test period of 226 days, the final capital for each strategy was determined, and annualized returns were computed to assess profitability over the testing period. The results showed that the hybrid model achieved a final capital of $376,610.16 with an annualized return of 751.32%. The benchmark model resulted in a final capital of $180,312.59, yielding an annualized return of 159.12%, while the buy-and-hold strategy reached a final capital of $166,420.74, with an annualized return of 127.65%.

Figure 4 presents the portfolio capital growth for each strategy, with the hybrid model, benchmark model, and buy-and-hold strategies represented by three distinct lines. The graph clearly shows that the hybrid model outperforms both the benchmark model and the buy-and-hold strategy, demonstrating its superior effectiveness in generating profitable trades based on price predictions.

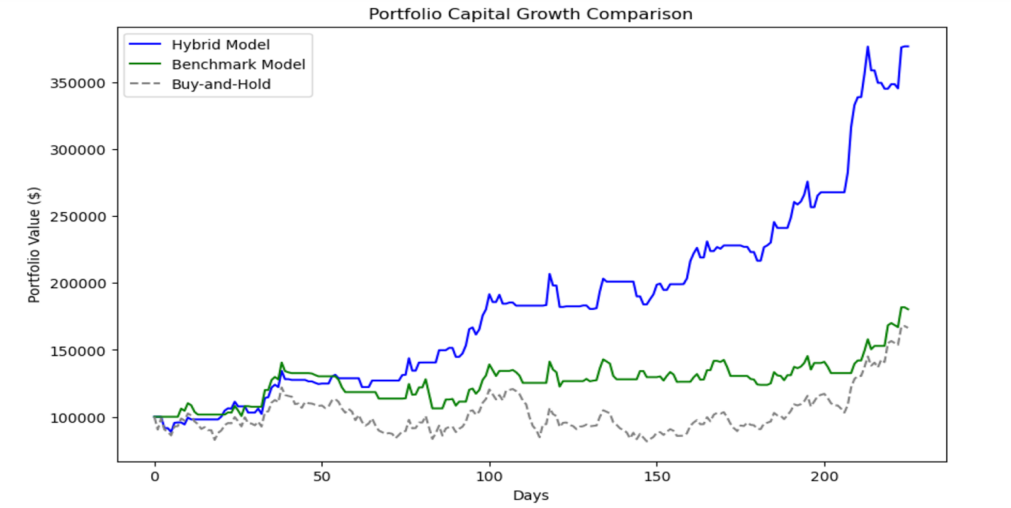
Figure 4: portfolio capital growth with respect to different trading strategies

5. Conclusion

In conclusion, this paper presents a novel hybrid VMD-Bidirectional LSTM model for predicting Solana's price, incorporating a range of market factors, such as Bitcoin price, Solana trading volume, and the Bitcoin halving event. By leveraging a hybrid approach, which combines VMD's ability to decompose time series data into multiple frequency modes and the predictive power of Bidirectional LSTM, the model achieves notable improvements in forecasting accuracy compared to traditional methods.

However, some limitations must be acknowledged. Firstly, the model relies on historical data and the assumption that past price trends and market factors alone can predict future price movements. While market factors like Bitcoin price and trading volume provide useful insights, external influences, such as regulatory shifts, technological innovations, and macroeconomic events are not considered, which could impact the model’s accuracy during unforeseen market changes. Also, the VMD technique, while effective in isolating different frequency components of the time series, might not fully capture all types of noise or sudden external shocks that can disrupt market behavior.

The VMD decomposition method used in our model extracts 10 different modes from the input data, each corresponding to distinct frequency components that represent various market dynamics. These modes capture both long-term trends and short-term fluctuations, enabling the model to better understand the complex nature of cryptocurrency price movements. The incorporation of these modes enhances the model’s ability to account for diverse patterns in the data and makes it more robust to varying market conditions.

Most importantly, the strength of the approach lies in its comprehensive framework. By combining fundamental factors (such as Bitcoin price and market volume), technical indicators (via VMD), and machine learning (through Bidirectional LSTM), the model offers a more holistic and nuanced prediction of Solana's price that has seldom been explored in the past. This integration of diverse techniques results in improved accuracy, flexibility, and robustness, particularly in handling the volatility and complexity inherent in the cryptocurrency market. Additionally, the trading simulation comparing different models provides strong evidence of the practical applicability of our approach. The results from this simulation demonstrate how our model not only outperforms traditional methods but also holds great potential as a trading support system. This makes it a valuable tool for both market analysts and traders, offering actionable insights to guide investment strategies in the highly unpredictable cryptocurrency landscape.

In summary, while there are areas for further improvement, particularly in expanding the range of external factors considered, the hybrid VMD-Bidirectional LSTM model represents a significant advancement in cryptocurrency price forecasting. It paves the way for future research that can integrate additional market indicators and refine machine learning models to build more reliable and scalable prediction systems for the crypto market.