1. Introduction

Accurate credit risk assessment remains fundamental to banking operations. Traditional models, including logistic regression and decision trees, depend on static features such as income, debt levels, historical defaults, and external credit scores [1]. While effective in filtering risky borrowers, these models fail to capture high-dimensional and dynamic customer behaviour. This creates a business dilemma: banks may inadvertently reject customers with uncertain behaviour who actually have high profit potential.

This study argues that behavioural uncertainty does not simply equate to risk, as high uncertainty often reflects data complexity or noise rather than inherently poor creditworthiness—yet conventional models remain unable to distinguish among such ambiguous groups. We therefore propose a new methodological framework that quantifies customer behavioural uncertainty using entropy derived from a DPMM and integrates this measure into a profit forecasting model.

The main contribution of this study lies in the first proposal and application of an entropy metric based on the Dirichlet Process Mixture Model (DPMM) to quantify customer behaviour uncertainty, introducing a new high-dimensional behaviour-oriented predictive paradigm to the field of credit risk control; Through rigorous statistical tests and visualisation analysis, empirical evidence shows that, after controlling for all traditional risk control variables, entropy still exerts a highly significant non-linear impact on credit profit margins (edf=3.887, p<0.001), revealing the independent mechanism by which information quality influences profit determination. The dynamic decision-making model constructed on this basis successfully identified a high-uncertainty, high-profit customer group that was underestimated by traditional models (with a profit difference of 12.2%), providing a practical strategic framework for financial institutions to transition from purely risk control to refined customer value management.

2. Methodology

2.1. Bayesian nonparametric framework

We adopt a Bayesian nonparametric (BNP) model to capture complex customer behaviour. BNP models allow complexity to grow with the dataset, in contrast to parametric models that require pre-specified cluster numbers [2]. The Dirichlet Process (DP) serves as the foundation, providing priors over infinite partitions. The DPMM extends this to clustering applications and has been applied widely in text mining [3], healthcare analytics [4], and finance. To visualize the uncertainty patterns within our customer data, we adapted techniques from the uncertainty visualization literature [5].

2.2. Data source

The dataset comprises over 30,000 loan applicants, including loan amount, income, demographic information, external credit scores (EXT_SOURCE_1, EXT_SOURCE_2, EXT_SOURCE_3), and default indicators (TARGET). After cleaning and merging external records, the effective sample size for modelling was 109,589 observations. To facilitate comparisons, we aggregated the three EXT_SOURCE variables into a composite measure, EXT_SOURCE_avg.

2.3. Profit function

We construct a proxy profit function defined as:

$$$ \begin{array}{c}Profit = Loan Income - Default Loss - Assumed Cost\end{array}$$$(1)

where:

· $$ \mathrm{L}\mathrm{o}\mathrm{a}\mathrm{n}\mathrm{ }\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}$$  = AMT\_CREDIT \times Interest\ Rate, with a fixed annual interest rate of 15%,

· $$ \mathrm{D}\mathrm{e}\mathrm{f}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{ }\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}$$  = AMT\_CREDIT \times TARGET,

· $$ \mathrm{A}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{ }\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}$$  = 5,000 per loan.

To control for loan size heterogeneity, the dependent variable is profit rate (profit divided by loan amount).

2.4. Entropy as uncertainty measure

Using DPMM clustering, each customer is assigned a posterior distribution over behavioural groups. Entropy is then defined as:

$$$ \begin{array}{c}H\left(\mathrm{i}\right)=-\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{p}}_{\mathrm{i}\mathrm{k}}{\log }_2\left({\mathrm{p}}_{\mathrm{i}\mathrm{k}}\right),\end{array}$$$(2)

where  $$ \mathrm{K}$$  is the number of clusters, the higher the value of  $$ \mathrm{H}\left(\mathrm{i}\right)$$  , the less clear the behaviour pattern of customer $$ \mathrm{ }\mathrm{i}$$  is, making it difficult to represent them with a single group, and thus increasing the uncertainty of their behaviour.

This measure primarily captures data uncertainty (intrinsic randomness in customer behaviour), complementing traditional static risk variables.

2.5. Statistical model: Generalized Additive Model (GAM)

To estimate the nonlinear effect of entropy on profits, we employ a GAM [6,7]:

$$$ \begin{array}{c}Profi{\mathrm{t}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}}~ \\ s\left(\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{y}\right)+ AM{\mathrm{T}}_{\mathrm{C}\mathrm{R}\mathrm{E}\mathrm{D}\mathrm{I}\mathrm{T}}+ AM{\mathrm{T}}_{\mathrm{I}\mathrm{N}\mathrm{C}\mathrm{O}\mathrm{M}{\mathrm{E}}_{\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{A}\mathrm{L}}}+ EX{\mathrm{T}}_{\mathrm{S}\mathrm{O}\mathrm{U}\mathrm{R}\mathrm{C}{\mathrm{E}}_1}+ EX{\mathrm{T}}_{\mathrm{S}\mathrm{O}\mathrm{U}\mathrm{R}\mathrm{C}{\mathrm{E}}_2}+ EX{\mathrm{T}}_{\mathrm{S}\mathrm{O}\mathrm{U}\mathrm{R}\mathrm{C}{\mathrm{E}}_3}\end{array}$$$(3)

The smooth function s(entropy) allows flexible nonlinear estimation of entropy’s contribution.

3. Analysis & results

3.1. Descriptive analysis

Customers were divided into high-uncertainty (top 20% entropy) and low-uncertainty (bottom 20%) groups. Table 1 summarizes profit comparisons.

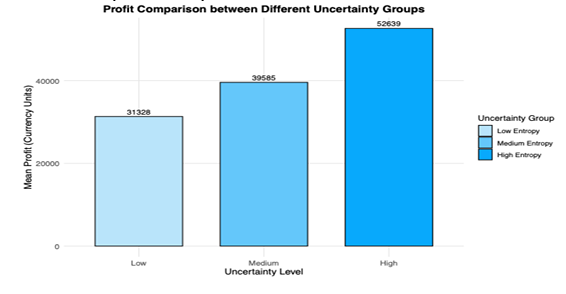
As shown in Figure 1, the profit comparison of different uncertainty groups indicates that the average profit of the high-entropy group (the top 20% of uncertain customers) is significantly higher than that of the low-entropy group (the bottom 20% of uncertain customers). This result further confirms the role of behavioral uncertainty in differentiating customer value. Customers with high uncertainty exhibit higher profit potential, which is consistent with the deep patterns captured by our entropy index.

According to Table 1, high-uncertainty customers show approximately 68% higher average profits than low-uncertainty customers. Through cross-validation using two different statistical test methods, the t-test and Kruskal-Wallis nonparametric test, we confirmed that the profit difference between the two groups was highly statistically significant. This preliminary finding strongly supports our core hypothesis that there is a positive correlation between uncertainty and profit.

3.2. GAM regression

Regression results indicate that entropy significantly and non-linearly affects profit. Parametric terms: Loan amount and external scores are all highly significant predictors. Smooth term: s(entropy), with edf = 3.887 and p < 0.001, confirms a complex nonlinear effect. Model fit statistics show Adjusted  $$ {\mathrm{R}}^2$$= 0.0588 and Deviance Explained = 5.89%. Though modest, these values are typical in behavioural finance contexts where noise dominates. Importantly, entropy’s effect remains robust.

Significance code：0 '' 0.001 '' 0.01 '' 0.05 '.' 0.1 ' ' 1

Table 2 presents the summary of the Generalized Additive Model (GAM) used to predict profit_rate. The results show that all parametric coefficients, including AMT_CREDIT, AMT_INCOME_TOTAL, and EXT_SOURCE_avg, are highly significant predictors of the profit rate. The loan amounts and total income of customers in the dataset range very widely, reflecting the diversity of the sample. The mean of the average external credit score (EXT_SOURCE_avg) is 0.506 and the standard deviation is 0.126, indicating that its distribution is relatively concentrated. The mean value of the core variable entropy is 0.618, and the standard deviation is 0.254. Its range is from 0.170 to 1.250, demonstrating different degrees of uncertainty in customer behavior. The mean of the dependent variable profit rate is 0.096, that is, the average profit rate is 9.6%, but its range is from -0.850 to 1.050, indicating that some loans may have led to losses.

According to Table 3, the smooth term for entropy, s(entropy), exhibits an effective degrees of freedom (edf) of 3.887, which is significantly greater than 1. This result provides strong statistical evidence that the relationship between entropy and profit rate is highly nonlinear. The low p-value (< 2e-16) further confirms that this nonlinear effect is statistically significant.

Table 4 shows overall model fit, with an adjusted R-squared of 0.0588 and a deviance explained of 5.89%, it is modest, which is common in behavioural finance given the inherent noise in customer data. However, the significance and nonlinear nature of the key predictor, entropy, remain robust.

3.3. Visualization

As shown in the figure, in low entropy regions, the predicted profit margin is close to zero or even negative. As entropy increases, the predicted profit margin rises rapidly. Once entropy reaches a certain level, the growth rate of the profit margin slows down. This figure perfectly explains why relying solely on linear models is insufficient and highlights the importance of the nonlinear relationships represented by entropy in profit forecasting.

To further explore the synergistic effect between customer uncertainty (entropy) and traditional risk control metrics (EXT_SOURCE_avg), we designed a unique dual-axis visualisation chart (see Figure 3). This chart aims to reveal how entropy modulates the impact of EXT_SOURCE_avg on customer predicted profit margins after controlling for all other variables.

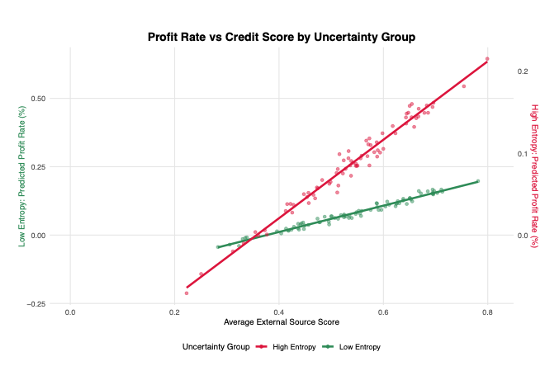
According to Figure 3, a dual-axis comparison of Average External Source Score (EXT_SOURCE_avg) reveals that entropy moderates the relationship between credit score and profit, clearly distinguishing two trends: a steeper slope for high-entropy customers and a more moderate one for the low-entropy group. This indicates that incremental improvements in credit scores lead to substantially larger profit increases among high-uncertainty customers, demonstrating a previously hidden synergy between behavioural uncertainty and traditional risk metrics captured by our model.

4. Discussion

This study reveals several key insights into the role of behavioural uncertainty in credit risk. Our analysis confirms that entropy is a statistically robust determinant of profit, exhibiting a clear and significant nonlinear effect. This finding reframes the conventional wisdom that uncertainty is solely a source of risk. In fact, high-uncertainty customers are not inherently bad risks; they often deliver higher profits due to characteristics like larger loan sizes or more favourable interest terms. Our research complements existing literature that has explored the link between uncertainty and profitability. Specifically, we provide quantitative evidence that supports the thesis of Chen et al. [8], who posited that profit can be derived from uncertainty. Our findings also align with the work of Agarwal and Zhang [9], who noted non-monotonic risk–return patterns, by offering behavioural uncertainty as a plausible explanation for this phenomenon.

From a practical perspective, our results offer tangible implications for the finance industry. First, the entropy metric enables more refined customer segmentation, allowing institutions to identify profitable segments that might be overlooked by traditional models, thereby providing a foundation for advanced analytical approaches such as those discussed in [11]. Second, this new metric can inform dynamic pricing strategies, where interest rates are adjusted according to a customer's entropy level, rather than solely based on the customer's static credit score. Ultimately, this framework provides a strategic tool for banks to achieve a better balance between risk control and profitability by enabling controlled exposure to previously unclassified, high-value customer groups, which aligns with the broader movement toward more adaptive and intelligent financial risk systems [12].

5. Conclusion

This study successfully introduces entropy, a novel uncertainty metric derived from Bayesian nonparametric clustering, to enhance credit profit forecasting. Our empirical analysis using a Generalized Additive Model confirms that entropy has a significant, nonlinear effect on profit rates, independent of traditional credit variables. This work reframes uncertainty not merely as a risk factor, but as a dimension of information quality that can reveal hidden profit opportunities. In practice, this research provides financial institutions with a new, robust decision-making tool to transition from a singular focus on risk aversion to a more holistic strategy of optimizing both profitability and risk management.