1. Introduction

There is a growing interest among Philosophers, Psychologists, Economists and Sociologists on the origin of cooperative behavior. Recently, the logistic costs have raised due to increase in competition between firms in the market. An efficient strategy for firms to eliminate possible loss from their rivals can be cooperation in bargaining games. There have always been times that firms need to take into consideration of possible actions of other firms. This is what is meant by a bargaining game: an attempt to achieve one’s goal in an environment where there are other competitors who have opposite or similar goals [1]. The degree of information exchange is very crucial in determining the responses carried out by players. Strategy depends on information about market conditions. More information means that the player is more better off at predicting others’ behaviors and eliminating possible losses. There are two types of games: simultaneous game and sequential game. In simultaneous games, each player has no prior knowledge of other opponent’s move. In sequential games, players may observe all or part of the opponent’s move. Almost all interactions between people can be viewed as forms of bargaining. For this research, we are going to investigate the bargaining model with perfect information.

2. Literature Review

2.1. Game Theory

In the past several decades, game theory has played an important role in the field of economics. It is a study of strategic decision making by understanding choice in situation among rivals. More formally, it can also be considered as a study of mathematical models of conflict and cooperation between decision makers. Game theory can be classified into two different big groups: Cooperative game theory and non-cooperative game theory. Cooperation game theory assumes that groups of players are the primary units of decision making, leading to cooperative behaviors. Whereas non-cooperative game theory assumes all of the players’ behaviors as individual actions done in strategic settings [2].

The main problems in game theory that aroused people’s attention are the movements of the game and the results generated by different preferences from other players. The major problem is the complete availability of information [3]. When the player engages in strategic behavior with other players, they are aware of other players’ cost functions. However, in this case, the responses from other players are fully confidential, thus adding difficulties to predict and determine other players motivations and costs [3].

Utility function served as a measure of a player’s happiness in a given situation. By analyzing each player’s cost function by maximization of the utility function, the players are able to make subjective prediction based on the results of probability. Every player in the market is constantly predicting the thinking of their competitors in order to carry out the best possible solution if there’s a change. This illustrated the concept of interdependence in game theory, which stated that players in the game are affected by what others behave and his actions must depend on the prediction of other players’ likely responses [4].

Cooperation in game theory is usually analyzed by Prisoner’s Dilemma. The success or failure of cooperation in Prisoner’s Dilemma is dependent upon the future play with the same player. One example of Prisoner’s Dilemma can be illustrated by Figure 1 below. As shown by the graph, two prisoners are separately interrogated. If they both deny charges, they can only be punished with circumstantial evidence. If one squeals on the other, he is rewarded with a sentence reduction and the other is punished hard. f both squeal, both receive hard sentences with some reward for collaboration. The dominant strategies of each player, which dominates any other choice regardless of strategy choices of other players, are also shown on the graph. Dominant strategy equilibrium in this case is: (squeal, squeal). If Roger and Oscar had both denied, they would both have been better off. So, outcome is what we will call Pareto dominated: There exists another outcome where at least one player is better off, and no player is worse off.

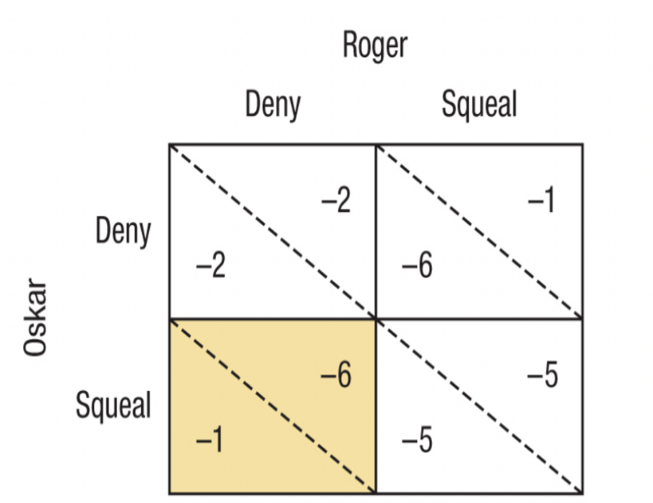
Figure 1: Prisoner’s Dilemma Example.

This classic interpretation of Prisoner’s Dilemma in the concept of Game theory is closely linked to the experiment that we are going to investigate, providing solid foundation when we delve deeper into the topic of ‘The degree of Information Exchange on the effectiveness and efficiency of cooperation in the bargaining game’.

2.2. The Model of Game Theory on Cooperative Utility and Efficiency

People normally think that if they communicate with each other more, the efficiency will be higher. In our research, we assume that this is our hypothesis: more communication will lead to more cooperative utility and efficiency.

In 1982, Mark Rubinstein used the method of dynamic game with perfect information to simulate the basic and indefinite bargaining process with perfect information. Based on this, he established the bargaining model with perfect information in turn, also known as the Rubenstein model.

In this model, two players will ask to split a cake. Player 1 makes the first offer, and player 2 can choose to accept or reject. If player 2 accepts, the game ends and the cake will be divided according to the player 1's plan; if player 2 rejects, he can make a bid, and Player 1 can choose to accept or reject. If player 1 accepts, the game ends, and the cake will be divided according to player 2's plan; if Player 1 says no, he will make another bid. The process will be continued until one player's bid is accepted by the other player. This is an indefinite perfect information game, where player 1 bids at odd number period and player 2 bids at even number period.

The preconditions of this model are that all the players are rational, and they get symmetric information. A Nash equilibrium is also based on these preconditions. A Nash Equilibrium is an outcome where both players are playing best response to the other player’s action without considering their opponents decision. However, people are not rational in real life, so does communication really improve productivity? This is the question that our research cares about.

3. Methodology

Our research topic is the degree of information exchange on the effectiveness and efficiency of cooperation in bargaining game.

In our research, we want to build a cause-and-effect relationship between cooperation and efficiency. We plan to design an experiment and collect qualitative data that collected by ourselves. We think experiment is a best way for us to study this research, because it can mostly prevent other confounding variables. However, maybe the gender and ages could be the lurking variables. The population of our experiment is unlimited. We choose it randomly and place them randomly in control and experimental group.

Also, our research is based on previous experiment, so we also used documentary method. Our experiment is based on the Rubenstein model and Nash equilibrium, but we modify it. We convert the model to experiment in real life.

By combing experimental method and literature method, the results of the research combine the advantages of both, and eliminate the disadvantages of both. Some confounding variables in the experiment, such as gender and ages, will be somehow eliminated after reading previous experiments and essays. And by improving and using previous experiments for reference, our results are somehow more accurate and well-founded.

We plan to let the independent variable of our research be whether people can communicate and the time of communication. Our dependent variable is the numbers of period used by players to divide the bread. The details of this experiment are in the next part.

4. Experiment Procedure

Here are two things that measure our outcome standard. The first one is the teamwork efficiency. It is the rate of successful distribution. The second one is communication symmetry. It is the time of discussion.

The experimental groups treatment groups:

Group 1: Three people will distribute 14 loaves of bread three times, each person will fill in an integer number for the number of loaves he/she wants to get, and the time limit is 30 seconds. People cannot communicate each time they fill in the bread, they only know whether the last distribution was successful or not.

Group 2: Repeat the experiment, except that before each experiment, people will have 30 seconds to communicate.

Control groups:

Group 1: Each person will fill in an integer number for the number of loaves of bread they want to receive for 30 seconds. If the number of loaves filled in by the three people is less than or equal to 14 loaves, they will receive their portion of the bread, and if not, they will not receive anything. Each time people fill in the bread, they cannot communicate with each other, they only know whether the last distribution is successful or not.

The game ends when the distribution is successful while at least ten time.

Group 2: Repeat the above experiment, except that before each experiment, people will have unlimited time to communicate until three people indicate that the communication is complete and the choice is over

For the experimentalists’ prize, the person with the most bread will receive $1 million, equally if two people get it, or $1 million each if the distribution is successful and all three have the same amount of bread. In the case of a full distribution, no one receives the prize.

Experiment analysis:

Our Expected outcomes are (1) Among the experimental groups, group 2 had a higher rate of successful assignment, with some people in each group betraying cooperation after success.

After communication, people will know what others think, and this will help them to make their own decisions. In the absence of knowledge of others' decisions, failure of allocation is highly likely, and it is optimal to ensure individual interests.

4.1. Rules

At the time of each assignment, other information about each participant, such as income, will not be available to others. Any form of off-site communication is prohibited and violators will be banned from the experiment. Also, no threats or assaults are allowed during communication, and violators will also be banned from the experiment.

4.2. Experiment Analysis

The study of social dilemmas is the study of the tension between individual and collective rationality. This is a non-zero game, in the control group, both groups will successfully complete allocation, but group 2 will reach successful allocation sooner, after which group 1, which has an infinite number of allocations, is more likely to behave in a betrayal manner. The experiment has an infinite number of allocations, so people are bound to succeed in allocation, and after having sufficient communication time, people are more likely to cooperate with others and therefore more likely to succeed, but one person's interests must be sacrificed in each allocation, so people may have different ideas to prioritize personal interests after analysis, and in the case where no one makes concessions, it is likely to produce allocation Failure.

4.3. Cooperative Behavior Reasons

Fairness tendency: Justice (fairness) is a foundation for all types of economic transactions, especially for strategic alliances that face a variety of internal and external uncertainty. Each distribution certainly requires trade-offs, but people can get the same number of shares when negotiated, and this makes those who tend to be fair to cooperate. [5]

4.4. High Information Symmetry

Although the game theory literature classically assumes perfect recall, players in business games often forget the past. This forgetfulness occurs partly because of the imperfect behavior of people, who forget past information. [6]. When information is public, people in the group know what others are giving, so people tend to give themselves to appear to fit in. People do not want to give more individually and get the same reward as others, and people do not want to be isolated or eliminated by others because they give less. Therefore, information disclosure helps people make choices by providing information about others.

4.5. Uncooperative Behavior Reasons

Own profit guarantee: Even though the highest allocators were all allocated the same high prize, participants who received the most slices of bread the first time may still not be the highest in the subsequent allocations by taking less, for example, if the other two cooperated resulting in the other participant not receiving the prize. In order to secure their own prize, choosing to take it all themselves is the safest decision and the motivation for choosing not to cooperate.

Expected person type: People choose to get less of the cake in order to ensure the success of the team assignment. These motives are roughly divisible into three broad categories: intrinsic, extrinsic, and image motivation. Extrinsic motivation is any material reward or benefit, either monetary or non-monetary. Extrinsic motivation is any material reward or benefit, either monetary or non-monetary, associated with giving, such as thank-you gestures and tax breaks. Image motivation, or signaling motivation, refers to individuals' tendency to be motivated partly by how others perceive them [7]. In this scenario, for intrinsic motivation, such individuals may be motivated to consider the interests of others, or for their own moral thinking. for extrinsic motivation, they choose to go for the whole thing in order to secure their own partial interests. For image motivation, they choose to sacrifice their own bread briefly in the hope of gaining the favor of others and also to get more bread for themselves in subsequent experiments.

Betrayal of allocation after successful allocation: Social dilemmas are situations in which individual rationality leads to collective irrationality [8]. Betraying cooperation in order to have exclusive access to the prize when securing the largest number of slices of one's own bread The exclusive bonus is the most rational choice. This is also the rational person in traditional economics.

The committed cooperator: This type of person will cooperate in a way that is completely consistent with the outcome of the discussion, such as a discussion that requires him or her to take less the first time and more later, and will ensure as much fairness as possible for himself or herself and others in the process.

Deliberate saboteurs: High bonuses still do not attract some people, and they will fill in excessive numbers in order to deliberately sabotage the collaboration so that others do not get the bonus. Such people cannot be avoided in the cooperation.

Efficiency promotion Strategy: The first principle is to change the payoffs of the game. That is, make it in your interest to keep your promises: turn threats into warnings and promises into guarantees. To do this, there are two major ways. [9]

1. Write down contracts to support your decisions.

2.Build and use reputation.

Both of these approaches can make it more expensive to break a promise than to keep it. The second principle is to change the game so that your ability to back-run a commitment is limited. In this regard, we consider three possibilities.

1. Cutting ties

2. Breaking the game

3. Let the outcome spiral out of control, or leave it to chance

These two principles can be combined: both the possible actions and their winnings can be changed. If a large commitment is split into many smaller ones, the benefit of breaking one of the smaller ones is likely to be insufficient to offset the loss of the remaining contracts. So we say, step by step forward.

The third principle is to use others to help you keep your commitments. It may be easier to build credibility with a team of two than with one person alone. It may be easier to build trustworthiness than one person alone. Or you can hire others to act in your place.

-Build credibility through a team

-Hire authorized agents

The first principle can be used in the experiment. You can Write down contracts. For example, each person needs to take a certain number of slices of bread per distribution, and if the contract is broken, you need to pay more than the bonus amount. This method is also effective in case of unlimited time, while it can only be completed if there is communication or a short time. Such a firm contract does regulate the behavior of the participants. Building and using reputation, on the other hand, may only regulate the behavior of others when people know each other. If one's reputation is extremely high, one may choose to cooperate for one's reputation.

The second principle is changing the game. For example, for the first approach-cutting ties, it is plausible for participants to refuse communication during The second approach Breaking the game, where communication is possible, allows one of the participants to communicate to the others that he will take most of the slices of bread, even if this leads to a failure of the collaboration, and choose to split the prize he receives equally with the others, while at the time of the actual taking he will choose to take the same number of slices as the others, making the joint bonus become more. In the case of a failure to communicate, you can also choose to take too many pieces and bet on the others to choose fewer pieces to maximize your benefit. Of course, Letting the outcome spiral out of control or leaving it to chance can also avoid other people who want to get more pieces, for example, by randomizing the number of pieces you choose so that even if you do or do not communicate, no one knows your decision.

Step by step forward is in the case of failure to communicate. This is a way to protect their bread slices. We can not predict the behavior of others. At the beginning to choose less, in the success of the distribution, can choose to continue forward. The third principle is to build a team, which may be challenging to achieve in a competition with only three people without the possibility of seeking intermediaries.

5. Conclusion

This study mainly discussed about the degree of Information Exchange on the effectiveness and efficiency of cooperation in the bargaining game. The broad concept of game theory was discussed then branched into topics of cooperative game theory and non-cooperative game theory. Prisoner’s Dilemma was further discussed to provide a fundamental understanding of the investigation. This study contributes to the literature of Rubinstein Model with perfect information in Game theory by adding our own knowledge and experiment of how the degree of information affect effectiveness and efficiency of cooperation. The idea of communication in strategic games draws our attention to the importance of allocative efficiency. By establishing an experimental group and a control group, with perfect information, players in the games are more likely to achieve profit maximization. However, allocative efficiency is also affected by instabilities of players’ behaviors. If the players are not willing to make concessions, even in the situation of perfect information, they would achieve a delayed allocative efficiency.

Types of motivation were also evaluated in the investigation to analyze the possible correlation between players’ strategic behaviors and extrinsic / intrinsic motivation. Motivation leads to interactive cooperative behavior, thus led to either success or failure of achieving allocative efficiency. Under this experimental setup, there is no doubt that incentive-based cooperative behavior served as a monolith in the concept of Rubinstein Model, which proven that the level of information exchange is crucial in achieving effectiveness and efficiency in a cooperative bargaining game.

Acknowledgment

All authors contributed equally to this work and should be considered co-first authors.