1. Introduction

With the rapid development of China's economy and the advent of the era of big data, the development of all walks of life is in a stage of rapid growth. Financial economy is an important part of the economic market, and its continuous improvement requires theoretical knowledge in the financial field. The application of arithmetic in finance is based on a series of financial or economic assumptions, using abstract mathematical methods to create mathematical models of financial operating mechanisms. As far as financial economy is concerned, financial mathematics is a basic content and the key to financial economic innovation and breakthroughs. Mathematics, as an important part of rigorous traditional science, has different application methods in various known social fields [1]. Under the current economic situation of rapid development in the financial field, financial mathematics, as an emerging economic discipline, has played a decisive role in its further development. In the process of operation and development, China's financial market has always followed the principle of safety, controllability, and mutual benefit, adhered to the concept of fair, just, safe, and stable development, and fully controlled the timing and strength of financial opening. At the same time, China has been actively promoting the opening of the financial market to the outside world, so as to add vitality to the domestic financial market, and the implementation of this measure has also provided support for the improvement of the development quality of the financial market. In addition, the degree of openness of the financial market is the fundamental reason for the development and growth of China's financial economy. As China's financial market continues to open to the outside world, more and more overseas financial institutions have begun to invest inward, carry out financial activities, and deepen international cooperation with Chinese financial institutions. The door to the financial market has been completely opened [2]. In this paper, the author introduces the history, basic concepts, and connotations of financial mathematics, analyzes two basic conceptual mistakes in financial mathematics, and explores innovative applications and prospects for the development of financial mathematics. Under the new situation of China's current economic development, further researching the application of financial mathematics in the financial market and broadening the specific application scenarios of financial mathematics will help promote China's financial market to a more scientific, fair, and open future.

2. History of Financial Mathematics

The history of the development of financial mathematics can be traced back to 1900. French mathematician Bachelier first used probability methods to study stock prices in his doctoral thesis "Theory of Speculation". Bachelier discovered that stock price changes are completely random, so he used the Brownian motion model to describe stock price fluctuations, which was 5 years earlier than the famous physicist Einstein described Brownian motion in mathematical language. Bachelier's research results were too advanced to attract the attention of academic circles. It was not discovered until 1955 by Samuelson, the first American to win the Nobel Prize in Economics. In the 1970s, with the continuous development of financial innovation, the use of mathematical models to price financial products became the focus of theoretical research. In 1970, Black and Scholes first assumed that stock prices obey Samuelson's geometric Brownian motion model, derived the famous B-S option pricing formula, and used mathematical tools to solve financial derivatives such as stocks, bonds, currencies, and commodities. The problem of reasonable pricing of the paper has achieved another major breakthrough in financial theory.

In 1973, Black and Scholes wrote an option pricing theory based on the B-S option pricing formula as a research paper entitled "Option Pricing and Corporate Debt" and published it in the Journal of Political Economy. This article quickly became one of the most important papers in the field of economics.

In 1970, Merton, a new colleague of Scholes's at the Massachusetts Institute of Technology, saw the work of Black and Scholes and immediately grasped the potential of the work. Merton was the only economist who mastered stochastic calculus at that time. He also derived the B-S option pricing formula with the stochastic calculus method, and further weakened the assumptions on which the B-S option pricing formula relied; at the same time, the Poisson jumping process is added to the geometric Brownian motion, thus expanding the application range of the B-S option pricing formula. Therefore, the B-S option pricing formula is also called the B-S-M option pricing formula.

Figure 1: HP Financial Calculator (source from the Internet).

HP (Hewlett-Packard) and TI (Texas Instruments) quickly developed hand-held calculators with built-in B-S option pricing formulas to calculate option prices (see Fig. 1). The Second Wall Street Mathematical Revolution has rapidly increased the number of innovative tools and innovative products in the financial market, and the financial market has achieved unprecedented development. In 1997, Scholes and Merton won the twenty-ninth Nobel Prize in Economics for this. Unfortunately, Black died young and did not receive the award together with Scholes and Merton.

3. Basic Concepts and Connotations of Financial Mathematics

Financial mathematics is also known as mathematical finance or analytical finance. Through mathematical modeling and other forms, based on the inherent laws and theoretical analysis of finance, financial mathematics uses mathematical tools as the carrier to guide practical activities [3]. This is an emerging discipline with distinct interdisciplinary characteristics. In short, financial mathematics is a cutting-edge economic discipline that perfectly combines modern technology and theoretical knowledge and complements each other. It is also an important analytical tool for modern financial markets.

Different from financial economics, the fields involved in financial mathematics are relatively narrow and the concepts are relatively abstract. In the stock market, financial economists often study the structural reasons for the current stock price of a certain company. Quantitative finance scientists will use financial mathematics theory to conduct a series of numerical analyses on current or historical stock prices, and then give a risk assessment of the company's stock, or calculate the fair price of related derivatives. ARBITRAGE, OPTIMALITY, and EQUILIBRIUM are the three basic ideas of financial mathematics, and the core content is to study investment portfolios, optimal choices, and asset pricing theory in stochastic environments. As far as the essence of financial mathematics is concerned, it belongs to an important branch of finance in the stock market [4]. Financial mathematics mainly studies the relationship between stock price fluctuations and stock price changes, and the impact of stock price changes on investors' decision-making behavior. This is also the so-called financial mathematics of the stock market. Therefore, the financial mathematics of the stock market is completely based on the financial theoretical environment and basis. The financial theory is an important support for financial markets.

4. Two Basic Conceptual Mistakes in Financial Mathematics

4.1. Errors in Price Calculation During Abstraction

The first step in solving practical problems or establishing scientific theories is to abstract practical problems into mathematical problems, and then apply deductive reasoning methods to draw conclusions that reveal the laws and characteristics of the motion of things or methods to solve problems. If there are basic concept errors in the process of mathematical abstraction, a series of wrong conclusions that do not match the facts will be drawn. Mathematical concepts are the thinking reflection of the human brain on the quantitative relationship and spatial form of objective things, and are also the cornerstone of establishing mathematical theories and other scientific theories. Although mathematical concepts are far away from the intuitive experience world, they can more deeply reflect the nature of the objective world. Mathematics usually uses the form of definition to clarify the connotation of mathematical concepts - the characteristics of the "quality" of the object, and its extension - the scope of the "quantity" of the object. If the connotation and extension expressed by mathematical concepts are misunderstood and misused, the established scientific theory is like a tall building with a weak foundation, and sooner or later it will collapse like a mountain shaking.

A random process X(ω,t) is a binary function defined on Ω×T. For a fixed time t, X(ω,t) is a function of state ω, called a random variable, denoted as X(t); for a fixed state ω, X(ω,t) is a function of time t, called Sample function or sample track, denoted x(t). A sample function x(t) corresponds to a "measurement result" in a random experiment, such as the stock price change process over time displayed by stock analysis software, so x(t) is also called a "realization" of the random process, as shown in Fig. 2 is a schematic diagram of the relationship among the random process X(ω, t), the random variable X(t), and the sample function x(t).

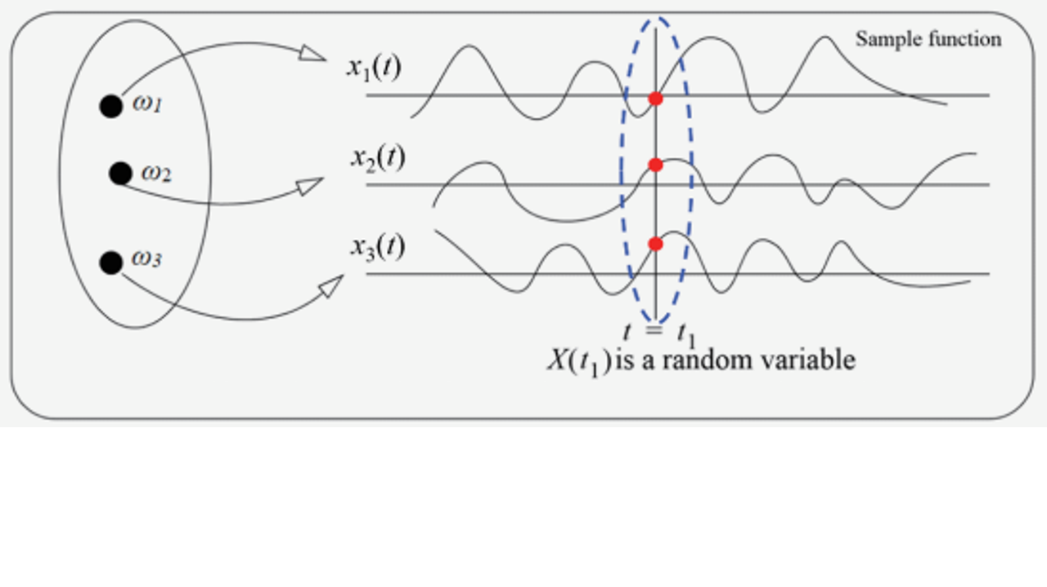
Figure 2: Stochastic Process Definition.

Observe the change process of the stock price s(t) with the time t, for any time value t, there is a uniquely determined s(t) corresponding to t, and the quantitative relationship between the stock price and time is "one-to-one correspondence". Therefore, the stock price s(t) is a function of the time t [1]. According to the definition of stochastic process, the stock price s(t) is a random process S(ω, t) when ω is fixed, and can only be abstracted as a sample track s(t) in the random process S(ω, t), rather than random variable S(t). Financial mathematics abstracts the stock price s(t) into a random variable S(t), which invisibly changes the research object from a sample track to a collection of sample tracks, causing the research object of financial mathematics to be misplaced, so the established price model cannot correctly describe the stock price phenomenon and comes up with the fallacy that "the stock price obeys the logarithmic normal distribution".

4.2. Wrong Definition of Volatility

Volatility is a very important input variable in the B-S option pricing formula. Option pricing theory first assumes that asset prices follow a lognormal distribution, and then defines the standard deviation describing the degree of dispersion of the normal distribution as volatility, and uses the standard deviation of the normal distribution to measure the volatility of asset prices [1]. From the definition of a random process, the standard deviation is a statistical parameter describing the degree of divergence of a set of sample orbits, and has no direct relationship with the degree of fluctuation of a sample orbit. Therefore, using the standard deviation of random variables to predict the volatility of stock prices is as absurd as physics uses temperature to measure the kinetic energy of a molecule. It is bound to fail to correctly predict financial market fluctuations, which will bring huge disasters to the financial market. In addition, financial mathematics uses the variance of random variables to measure risk, which means that financial mathematics also regards large upward fluctuations in stock prices or the situation in which investors obtain excess returns as risks. No wonder Taleb, the author of the best-selling book "Black Swan", said that "financial mathematics harms the financial system by creating risks."

5. Innovative Applications of Financial Mathematics

5.1. Optimize Financial Business Processing

Although there are still many problems in the development of the financial market, the innovative application of financial mathematics has become a guarantee for development and has played a role in stabilizing the market environment. However, in the future, it is still necessary to apply financial mathematics to optimize business processing and other aspects, so as to carry out all-round innovation and maximize the effectiveness of financial mathematics. In the current era of advanced information, traditional financial services and work processes are no longer applicable, especially the relatively cumbersome procedures and economic interaction models, which should be improved and perfected through financial mathematics [5]. Since financial mathematics is the combination of computer equipment and mathematical theory, it can accelerate the development trend of electronic financial business and ensure that the public has fewer procedures and faster speed in the financial market. At the same time, it strengthens the efficiency of financial business processing and feedback, which shows that financial mathematics plays a huge role in business processing.

5.2. Establishment of Financial Database

In the current era of data information, market development can be controlled by making good use of data information, especially the financial market with a huge amount of information, which requires strong collection and organization capabilities. Therefore, it is necessary to establish a database based on financial mathematics, carry out real-time control of data in the financial market, and provide support for various economic activities and financial services. For example, the all-round application of big data provides guidance for market development through the establishment of financial databases, lays a solid foundation for future development, and promotes the development of financial markets in the direction of standardization and refinement. In addition, the establishment of the database can provide more guarantees for financial entities, such as the security of financial services and the convenience of financial services. In the process of financial market development, the development curve of database performance can also be used to provide references and bases for market participants. The financial database mainly collects market information, thoroughly solves problems in market development, and builds a sound financial system.

5.3. Comprehensive Analysis of Mathematical Models

The application of financial mathematics has played an important role in the development of the market, including the construction of mathematical models, the maintenance of the market order, and the guarantee of new financial industries, such as stocks, securities, and insurance. Mathematical models can accurately analyze the development trend of the financial market and provide reference and judgment for participants. Meanwhile, in the case of establishing financial market rules and regulations, mathematical models can be used for analysis to ensure that the rules and regulations can operate effectively and stabilize the current financial market environment. In addition, the construction of mathematical models can reduce the risk of financial market crashes, and provide effective support for the implementation of various policies [6]. With the help of data information, it can develop in the right direction, which also shows the role and value of financial mathematics.

6. Prospects for the Development of Financial Mathematics

6.1. Increasing Complexity of the Problems to be Solved

The application process of financial mathematics is mostly focused on building models and carrying out analysis and research on financial problems through models. However, financial mathematics has virtual characteristics, so when building a model, it is often completed under assumptions, and naturally, there will be situations that do not match the actual situation or conflicting content. Therefore, the results of using financial mathematics to solve problems are not ideal, and problems that affect market development often occur. Therefore, to maximize the effectiveness of financial mathematics, there is a need to increase the research and improvement of mathematics [4]. For example, the CAPM (Capital Asset Pricing Model) theory is only applicable to European-style options, which is quite different from the development of China's financial market, so the CAPM theory cannot be directly applied. In-depth research should be carried out based on this theory, and a theoretical system that is in line with the development of China's financial market should be innovated, so as to maximize the value of financial mathematics.

6.2. Empirical Research Development Emerging

In the future, financial mathematics should be developed in the direction of current affairs research, and the empirical research process should be mainly analyzed on the basis of mathematical investigation. For example, when constructing a financial market model, it is necessary to conduct in-depth investigations in the market environment to ensure that more accurate data information can be obtained, and the constructed mathematical model will be relatively true and complete [5]. If the mathematical model is established without comprehensive investigation, then the model can only be established with the help of theoretical analysis, and it will lack the support of data information, which directly makes it difficult for the model to be close to the current market development status, and it is impossible to analyze the development law. Therefore, in the process of financial mathematics research, it must develop towards the empirical direction and play the greatest role in the financial market.

6.3. Financial Mathematics Sustainability

The development of the financial market is relatively complex, and it is difficult to accurately capture the laws. This also means that the financial market has characteristics such as nonlinearity and randomness, which also puts forward a higher standard for the application of financial mathematics. For example, when the financial market fluctuates significantly, randomness will also be strongly presented, which will eventually lead to asymmetric information and data in the financial market and reduce the application effect of financial mathematics. Many experts at home and abroad have begun to study this issue and put forward the geometric Brownian motion theory, which can analyze the current situation of the financial market more accurately and capture the development law precisely even if there are abnormal fluctuations. It can be seen that financial mathematics is still in a continuous development trend and will be adjusted according to changes in the financial market in the future.

7. Conclusion

The development of the modern financial market is inseparable from the support of science and technology, especially the financial mathematics combined with the mathematical theory and computer technology, which optimizes and improves the financial work process and appropriately expands the financial market, including stocks, insurance, and other comprehensive financial fields. At present, the comprehensive application of financial mathematics can promote the transparency of data in the market and use precise mathematical theories to prevent various risks, presenting the current financial market curve and providing participants with data information to fully judge the financial market conditions and environment. It can be seen that financial mathematics has provided the development momentum for the entire market and also stimulated the vitality and potential of the market. This kind of high-precision analysis and calculation has played a positive role in the development of China's financial market.