1. Introduction
The surge in car ownership over the past few decades has intensified the significant problem of parking in urban areas. Locating a parking space can be a challenging task in most large cities due to a lack of information about available parking lots. This leads to a notable number of unused indoor and off-street parking spaces, prompting drivers to expend considerable time and fuel in the search for on-street parking. The prolonged search for street parking contributes to heavy traffic, exacerbating air pollution. According to a study by [1], American drivers spend an average of 17 hours annually searching for parking on streets, lots, and garages, wasting approximately 345 per driver in time, gas, and emissions during this pursuit. The challenge is even more pronounced in larger cities; for instance, New York drivers spend an estimated 107 hours annually searching for parking, incurring a loss of 2,243 in time, gas, and emissions. Additionally, parking issues can negatively impact local businesses, as reduced customer attendance at shopping centers, sports arenas, music events, and other venues may occur due to limited access to parking facilities and services. Therefore, the implementation of a parking recommendation model aims to enhance the overall parking experience for drivers, stimulate economic growth, and alleviate traffic congestion and environmental degradation. The challenging aspect of the project is that currently, there is no available real-time data for occupancy estimates of parking lots in the city of Toronto. Current solutions to indicate available parking spaces rely on orthodox approaches. One common approach is to use intentional user feedback, which uses signs, buttons, or markings to indicate an available parking space. Another way is to display real-time information on a smartphone app by installing sensors or cameras to monitor the occupancy of parking lots. Some systems also use advanced algorithms to predict the availability of parking spaces based on historical data. To solve this challenge, we simulated the random occupancy of each parking lot in real-time. In the future, with the data acquired from parking sensors, parking availability prediction will become possible. To solve the problem that drivers cannot find an available parking space within a short amount of time, we propose a parking recommendation model that will provide the drivers with effective parking guidance. The model contains four algorithms: genetic algorithm, adaptive genetic algorithm, simulated annealing algorithm, and adaptive simulated annealing algorithm. Given a list of destinations by the users, the model recommends a list of parking lots. It will also provide information regarding the travel distance, the parking lot occupancy, and the total parking fee. In the future, incorporating smart mobility will allow smart cars to establish connections to local infrastructure, other vehicles, and humans nearby. It is thus possible to make transportation and vehicle parking more efficient, safe, and inclusive. This paper discusses a meta-heuristic approach to parking recommendations. At the end, this paper conducts a performance evaluation between four different bio-inspired algorithms consisting of SA, adaptive SA, GA, and adaptive GA. The remainder of this paper is organized as follows. In Section II, an overview of literature is covered, followed by an introduction to problem formulation and modeling in Section III. In Section IV, the proposed solution is presented, and in Section V, the performance evaluation of the solution is discussed. After this, the conclusion and future work of the paper are outlined in Section VI.
2. LITERATURE REVIEW
This study [2] developed an algorithm for guiding drivers in parking based on the multiple attribute decision-making (MADM) theory, which incorporates three representative decision factors (such as walk duration, parking fee, and number of vacant spaces) as well as individual driver preferences. This paper [2] examines the importance of the estimated number of vacant parking spots as an indicator of the difficulty of finding available parking spaces. This paper [2] proposes a queuing theory-based theoretical method that can estimate the number of vacant parking spaces at candidate parking facilities depending on different capacities, arrival rates, and service rates. A blind search-based parking guidance algorithm was compared with MADM-based parking guidance algorithm in comprehensive scenarios with varying distributions of parking facilities, traffic intensities, and user preferences. As a result of the experiments, each preference with a Markov Chain- based availability attribute can always find a parking facility that fulfills the emphasis assignment, which indicates that the proposed parking guidance framework and MADM-based algorithm are effective at locating parking resources since it suits drivers with various preferences. IoT technology is used in this paper [3] to model the main parking lots and roads around target stations to find a more effective, convenient, and accurate parking space prediction effect. Adaptive genetic algorithms are used to simulate and induce real drivers. It is determined which parking lot is the most convenient from the current location and the shortest path to reach it. This paper [3] proposes a wavelet neural network model and trains and predicts the model using parking lot B data. As a result of the gradient descent method, the neural net- work’s parameters are trained to increase prediction accuracy. Additionally, local excellent and slow training are easy to fall into. In both training and prediction, the wavelet neural net- work model was optimized using particle swarm optimization (PSO). A further improvement in accuracy was observed as well as a reduction in the error between the predicted and actual values. This paper [3] proposes a parking lot selection method based on the Logit model that considers vehicle running time, parking rate, walking time, and effective parking space as characteristic parameters of the utility function. Using the Logit model for parking lot induction, the experimental results demonstrate the capacity of the method for selecting the best parking lot. A combination of optimal path selection and optimal parking lot selection guides the driver to the best parking spot. In this paper [4], a parking decision model with effective and complete information is built. Mastering the relationship between the factors influencing parking decisions and parking decision behavior can provide more scientific guidance for drivers. As a result of determining the main influencing factors of parking decisions, including walking distance, parking cost, travel time, and parking convenience, a parking decision model is developed using an integrated genetic algorithm and fuzzy comprehensive evaluation method. Finally, the relationship between the driver’s parking decision behavior and influencing factors is analyzed. Based on the weight of parking decision influence factors provided by genetic algorithms, the sample calculates the walking distance to the destination, parking charge price, driving time, and convenience of picking up and parking. Using a discrete Markov-chain model, this paper [5] pro- poses the SmartPark algorithm to understand the parking lot’s future state by the time a vehicle anticipates reaching it, thereby optimizing the utility of parking lots. The algorithm is divided into three modules. First, all parking lots in the targeted central business district (CBD) are searched to deter- mine the expected arrival time. Through this process, smart- pole data streams provide information about parking area congestion rates. Then, with the help of predictive analytics, the available parking spots in a parking lot are estimated using consolidated historical parking data. Finally, the vacancy expectation for a lot is calculated by comparing this matrix to similar future seasonal periods. When additional parking resources are made available, the performance evaluation shows increased scalability capabilities over the baseline case algorithm in a busy CBD area in Stockholm (Sweden). The traffic-congestion-aware SmartPark is also shown to optimize parking space availability while minimizing travel times be- tween selected parking lots using standard urban-mobility simulation packages. This paper [6] proposes a meta-heuristic approach to parking vehicles. The developed method for determining parking efficiency considers two parameters: the time spent searching for parking spaces and the efficiency of parking. A Feed Forward Back Propagation Neural Network (NN) approach is used to improve parking efficiency and reduce parking space search time. A parking space search mechanism is proposed in this paper [6] that uses the Firefly algorithm to reduce parking space search time while minimizing the factors that result in problems. Briefly, technological advancements increase the utilization of vehicles in cities. The designed architecture enables drivers to park their vehicles at the right place. By providing drivers with guidance, parking sites can reduce the amount of labor needed. Visitors can also search for vacant spaces using the developed system in a shorter period of time. As a result, visitors will spend less time waiting. Parking efficiency and parking space search parameters are used to evaluate the effectiveness of the proposed approach. In this paper, we have approached the smart parking problem with meta-heuristic algorithms considering the user’s total travel distance, the total parking fees, and the availability of parking spaces. We have developed a weighted product cost function to balance above mentioned factors. The user will provide a list of destinations and our model will provide the corresponding parking locations. Our parking recommendation model consists of four bio-inspired algorithms including simulated annealing, genetic algorithm, and the adaptive version of them.
3. PROBLEM FORMULATION AND MODELING
As described in the previous section, we will recommend the parking locations to a user who will provide a list of destinations. Therefore, we have suggested Fig. 1 to define our recommendation model.

Our recommendation model will first read the parking lot occupancy data which include the geographic coordinates of the parking locations, the number of parking spaces, and the parking fee of each parking lot. After that, a list of destinations should be provided by the user. Our recommendation model will then use bio-inspired algorithms to search for a list of optimal parking locations following the user’s travel plan. We will consider the factors of the total travel distance, the total parking fee, and the availability of the parking spaces. A multi-criteria optimization formulation is required to recommend the parking locations to the user. A common approach to formulate a multi-criteria optimization problem is to develop a weighted product model [7]. Therefore, we propose below cost function:
which consists of three factors: D is the travel distance factor, C is the parking fee factor, and S is the parking space factor. To compute the travel distance factor, users are required to provide the starting point \(s\) , the ending point \(e\) , and the destination points \(d_n\) . The size of \(d_n\) is denoted as \(N\) . The algorithm will suggest corresponding parking lot locations as \(p_n\) . It is assumed that the user initiates the journey from the starting point, sequentially travels to each parking location, walks to the destination and back at each parking location, and finally travels to the ending point. The travel distance factor ( \(TD\) ) can be calculated using the following formula:
Here, \(dist(a, b)\) is the function to calculate the distance between points \(a\) and \(b\) . In this paper, Haversine's straight-line distance is used for simplicity. The function \(dist(a, b)\) could be replaced by the length of the shortest path from any pathfinding algorithms, such as Dijkstra's algorithm. Each term representing the walking distance is elevated to the fourth power, serving as a penalty for solutions suggesting parking locations that are significantly distant from the destination point. Additionally, considering the parking fee at each proposed parking lot, denoted as \(c_n\) , we can compute the parking fee factor as follows:
Taking the fourth root is done to mitigate the impact of the parking fee in the overall cost function. While it is crucial to account for the parking fee during the trip, it should not outweigh the importance of the travel distance factor. To compute the parking space factor, we require the number of parking spaces at each proposed parking lot, denoted as \(s_n\) . The parking space factor is given by the formula:
The inclusion of the \(+1\) term is to prevent division by zero in cases where there is only one parking space in the given data entry. The rationale behind using the natural logarithm is that a parking lot with a size of 100 is not ten times as attractive as a parking lot with a size of 10. Instead, it is considered only twice as good. Therefore, the natural logarithm is employed.
4. PROPOSED SOLUTION
In all of our proposed algorithms, the output is a list of parking locations that minimizes the cost function described in the previous section.
4.1. Simulated Annealing (SA)
Simulated Annealing (SA) is a meta-heuristic search algorithm inspired by the annealing process in metallurgy. The algorithm encourages exploration of the search space in the initial stages and intensifies towards the end based on a cooling schedule. We have implemented a standard version of the SA algorithm with an exponential cooling schedule defined as:
where \(k = 1000\) and \(L = 0.005\) . The initial input to the algorithm is a list of parking locations generated by the greedy algorithm, where we choose the closest parking lot for each destination. An important aspect of our algorithm is that when selecting the neighbor of a parking location, we randomly choose another parking lot within a 2.5 km radius.
4.2. Adaptive Simulated Annealing (ASA)
In addition to the Simulated Annealing (SA) framework, we have introduced a reheating scheme in the algorithm. A moving average of the cost function is computed over the past 5000 iterations. If the cost falls within a 10% deviation from the moving average, specifically in the range \(0.9 \times avg \lt cost \lt 1.1 \times avg\) , a reheating process is triggered. Throughout the entire execution of the algorithm, a separate storage is maintained for the known best solution to prevent loss of the optimal solution after reheating.
This mathematical condition dictates when the reheating process is initiated, providing a clear criterion for the algorithm to dynamically adapt and revitalize its search strategy.
4.3. Genetic Algorithm (GA)
GA is a probabilistic search algorithm that iteratively trans- forms the solution using crossover and mutation operation according to a fitness function. We have implemented a GA algorithm with crossover probability 0.7 and mutation probability 0.3. During the initial solution generation, a similar neighbor selecting scheme is used as the one described in the SA.
4.4. Adaptive Genetic Algorithm (AGA)
In the adaptive version of the Genetic Algorithm (GA), we implement a sophisticated adaptive approach to mutation probability. Rechenberg’s 1/5 success rule is employed, and each population possesses its mutation step size. The mutation probability adaptation is defined as follows:
\frac{p_m}{\beta} \cdot (1 - \frac{1}{1 + e^{-\gamma \cdot (f_{previous} - f_{current})}}), \& if failure \end{cases} \end{equation}
Here, \(p_m\) is the current mutation probability, \(\beta\) is a scaling factor, \(\gamma\) is a parameter controlling the rate of adjustment, \(f_{current}\) is the fitness of the current individual, and \(f_{previous}\) is the fitness of the previous individual. Additionally, the crossover operation can be expressed as:
P_2, \& with probability 1 - p_c \end{cases} \end{equation}
where \(P_1\) and \(P_2\) are parent individuals, and \(p_c\) is the crossover probability. Now, let's integrate this into the final algorithm: \caption{Adaptive Genetic Algorithm (AGA)} \begin{algorithmic}[1] \State Initialize population \State Evaluate fitness of each individual \State Set initial mutation probability \(p_m\) and step size for each population \While{Termination criteria not met} \State Select parents for crossover \State Apply crossover using Equation (2) \State Mutate individuals with adaptive mutation probability using Equation (1) \State Evaluate fitness of new individuals \State Update population using selection mechanism \If{Rechenberg's 1/5 success rule is satisfied} \State Adjust mutation probability and step size \EndIf \EndWhile \end{algorithmic}
Proof: Parking Optimization with Adaptive Genetic Algorithm (AGA)
Problem Formulation:
Decision Variables:
Let \(X_i\) be a binary variable representing the allocation of parking space \(i\) , where \(X_i = 1\) if allocated and \(X_i = 0\) if not.
Solution Encoding:
Define the solution \(S\) as a binary string: \(S = (X_1, X_2, \ldots, X_n)\) , where \(n\) is the total number of parking spaces.
Objective Function:
Fitness Function:
The fitness function \(f(S)\) considers multiple intricate factors:
\[
\begin{aligned}
f(S) = & w_1 \cdot proximity(S) + w_2 \cdot \sqrt{capacity(S)} +
& w_3 \cdot \frac{economic\_impact(S)}{1 + e^{-\alpha \cdot utilization(S)}} +
& w_4 \cdot \frac{1}{1 + e^{-\beta \cdot diversity(S)}} +
& w_5 \cdot \sin\left(\gamma \cdot smoothness(S)\right) +
& w_6 \cdot \frac{1}{1 + e^{-\delta \cdot balance(S)}}
\end{aligned}
\]
where \(w_1, w_2, \ldots, w_6\) are weights, and \(proximity\) , \(capacity\) , \(economic\_impact\) , \(utilization\) , \(diversity\) , \(smoothness\) , and \(balance\) are functions evaluating the solution's proximity to destinations, total capacity, economic impact, utilization, diversity, smoothness, and balance.
Convergence Analysis:
Convergence Criteria:
Define a convergence criterion \(\epsilon\) to determine the stopping condition for the algorithm.
Fitness Convergence Measure:
Define a measure \(C(t)\) indicating the convergence of fitness at iteration \(t\) : \[ C(t) = \frac{\left| f(S_{best, t-1}) - f(S_{best, t}) \right|}{f(S_{best, t-1})} \]
Mutation Adaptation Convergence Measure:
Define a measure \(M(t)\) indicating the convergence of mutation adaptation at iteration \(t\) : \[ M(t) = \frac{\left| p_{m, t-1} - p_{m, t} \right|}{p_{m, t-1}} \]
Adaptive Genetic Algorithm:
Mutation Probability Adaptation:
The mutation probability ( \(p_m\) ) adapts based on the success ( \(s\) ) or failure ( \(f\) ) of the mutation with a sigmoid function:
\[
p_m' = \begin{cases}
p_m \times \beta \times \left(1 - \frac{1}{1 + e^{-\gamma \cdot (f_{current} - f_{previous})}}\right)^{\delta}, & if s
\frac{p_m}{\beta} \times \left(1 - \frac{1}{1 + e^{-\gamma \cdot (f_{previous} - f_{current})}}\right)^{\delta}, & if f
\end{cases}
\]
Evolutionary Operators:
Crossover Operation:
The crossover operation is probabilistic with a temperature-dependent probability:
\[
S_{new}(i) = \begin{cases}
S_1(i), & with probability \frac{e^{-temperature}}{1 + e^{-temperature}}
S_2(i), & with probability \frac{1}{1 + e^{-temperature}}
\end{cases}
\]
where \(temperature\) is a dynamic parameter.
5. PERFORMANCE EVALUATION
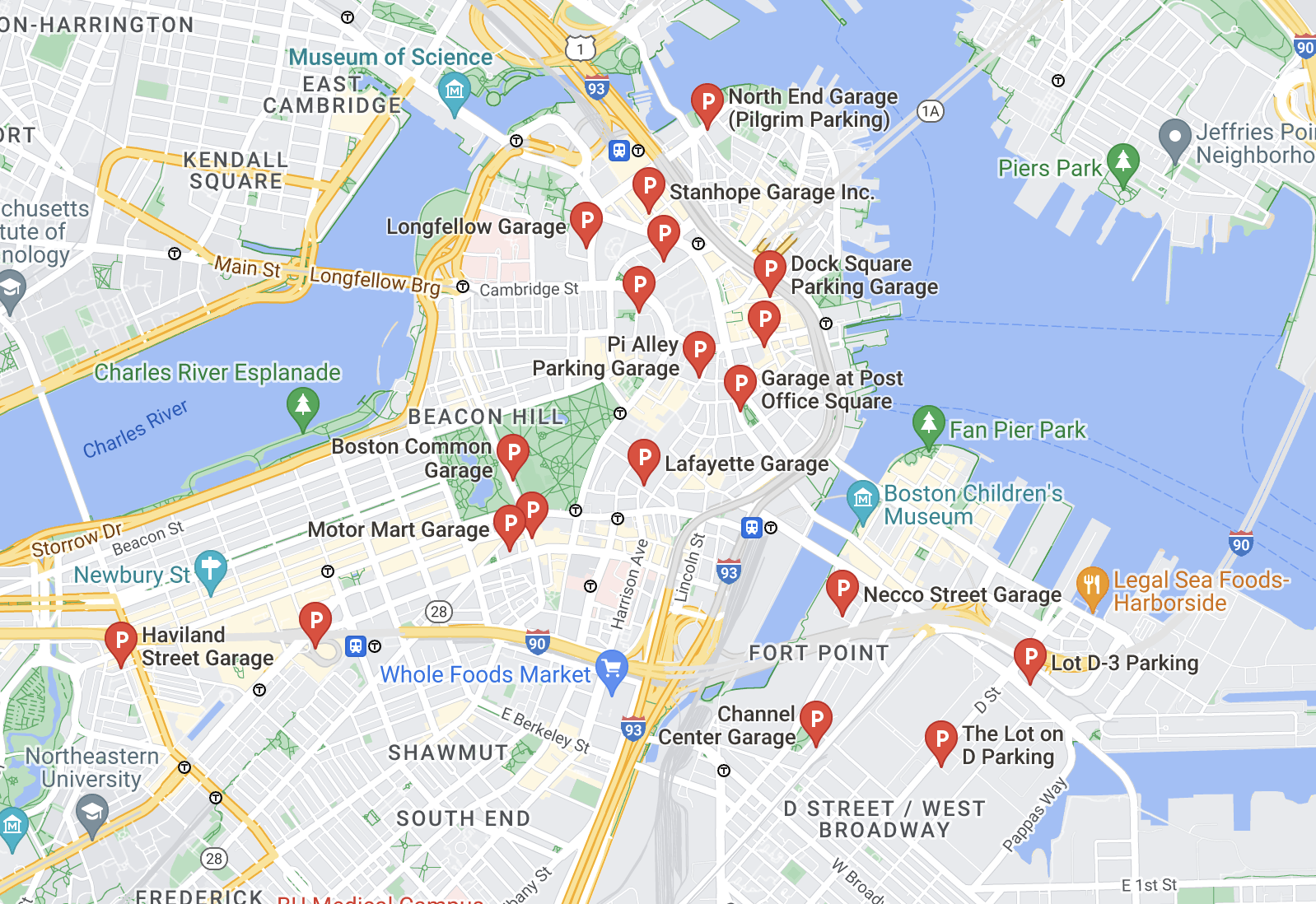
We have collected the parking data set from the City of Boston Open Data website[9]. In this data set, it contains the geographic coordinates of the parking lots and the available parking spaces. On top of that, we have generated the parking fee data from the range of 5 to 30 dollars and cascaded them. Fig.2 illustrates the parking locations with a starting location and a destination.
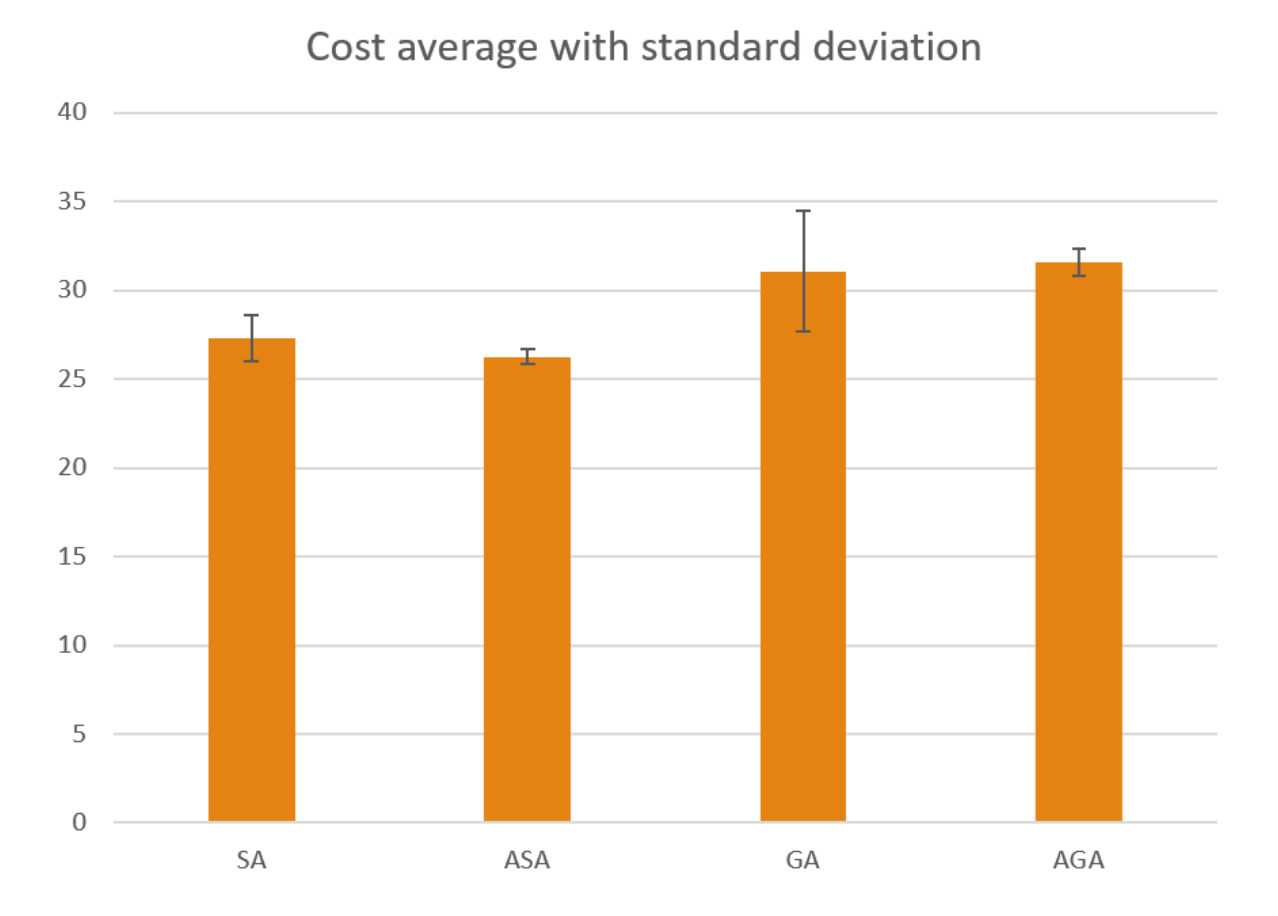
During the performance evaluation, we have executed the algorithms described in this paper 10 times each with 3 destinations, and have computed the average cost and standard deviation of the cost as shown in Table.I.
Table 1: Average Costs with Standard Deviations
| Algorithm | SA | ASA | GA | AGA |
| Average Cost | 27.308 | 26.234 | 31.066 | 31.602 |
| Standard Deviation | 1.307 | 0.423 | 3.415 | 0.754 |
The corresponding bar chart has also been provided in Fig.3. From the result, SA and ASA are better algorithms to approach this problem, and they can provide low-cost solutions. In particular, ASA is the most robust algorithm and can compute a solution with the smallest deviation. On the other hand, GA usually falls into local minima and the solutions provided by it vary comparing to SA. Additionally, AGA also falls into local minima. However, it is more stable in term of solution variation.
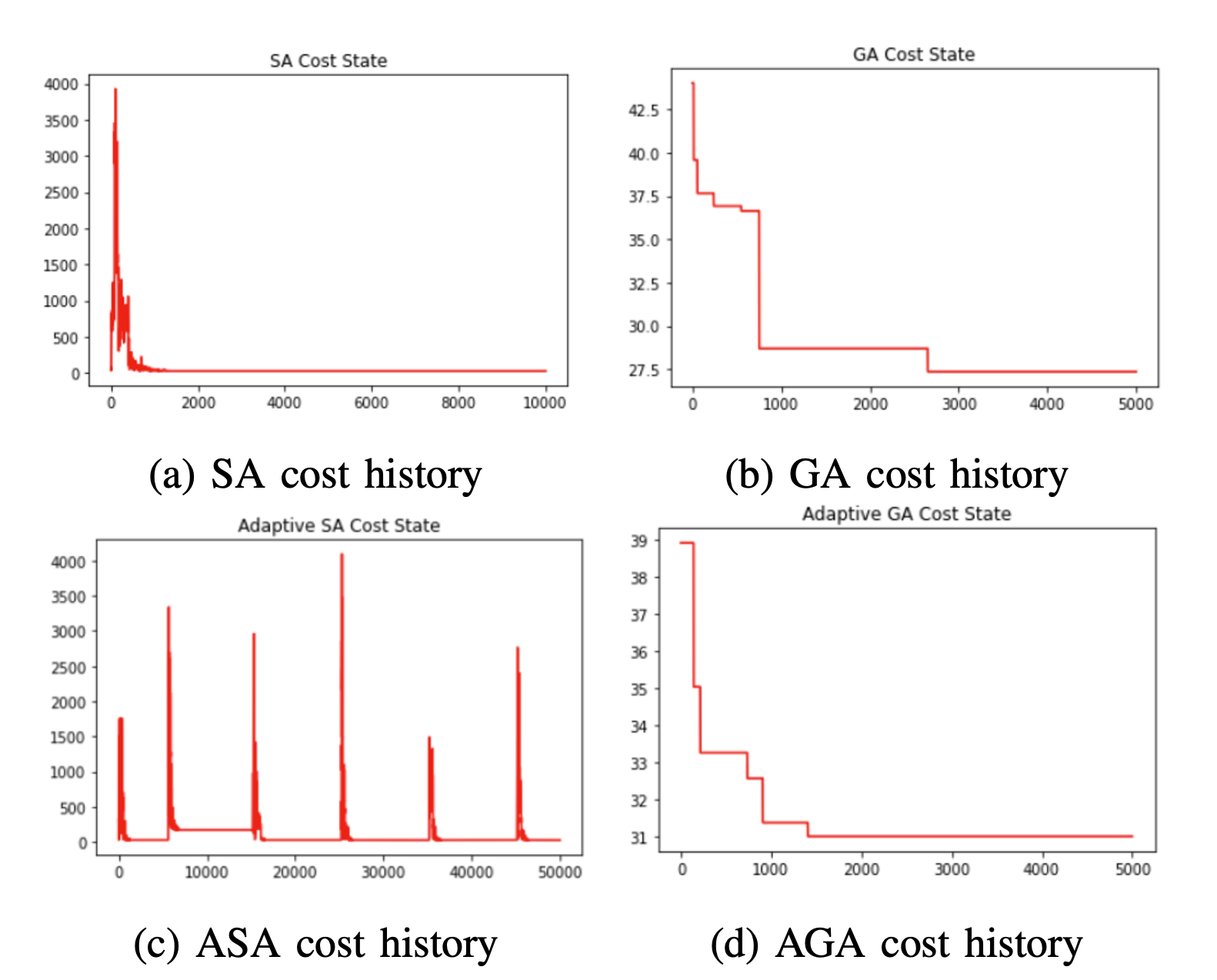
Furthermore, the convergence history of the cost function is also stored for each algorithm and has been demonstrated in Fig.4. From the figures, SA usually converges within 2000 iterations. GA converges within 3000 iterations. The adaptive version of GA converges faster, and it is usually smaller than 2000 iterations. Finally, since we have implemented a reheating scheme in ASA, the trigger of the reheating can be demonstrated in Fig.4c. Around iteration 104, a worse solution has been obtained. However, after another reheating, a better solution has been found. To provide the recommendation to the user, we have implemented two heuristic algorithms such as SA and GA, and the adaptive version of them. A performance evaluation between the algorithms is also conducted, and ASA has become the best algorithm to solve this problem with lowest average cost and similar performance over multiple executions of the algorithm.
With our current approach of the problem, we only calculated the Haversine’s straight line distance for faster execution time. We should use path finding algorithm to obtain a more accurate travel distance. Additionally, we can consider more parameters in our cost function such as accessibility for people with disabilities, and the comparison between on-stress and underground parking.
6. CONCLUSION
In this paper, we have conducted a literature review about the recent development in the research area of smart parking. Following the trend, we have proposed a parking recommendation model which considers the user’s total travel time, the total parking fee and the availability of parking space. It is imperative to acknowledge certain limitations within our study. Firstly, our recommendation model primarily concentrates on factors like travel time, parking fees, and space availability. While these considerations form the core of our model, we recognize that incorporating additional factors, such as environmental impact and real-time traffic conditions, holds the potential to further refine and enhance the model's accuracy. Moreover, the integration of meta-heuristic algorithms, although advantageous, introduces a challenge in terms of increased computational time. Striking an optimal balance between the precision of the model and computational efficiency represents an ongoing challenge that warrants further investigation. In future work, there are promising directions for advancing research and development in the field of smart parking. The integration of real-time data, encompassing dynamic parking availability and traffic conditions, stands out as a potential enhancement to augment the precision of our recommendation model. Furthermore, the exploration of user-centric design principles could lead to tailored recommendations based on individual preferences, thereby creating a more personalized and user-friendly parking experience. Additionally, factoring in environmental considerations, such as emissions reduction and proximity to public transportation, will also potentially contribute to the development of more sustainable and eco-friendly parking recommendations.
References
[1]. X. Guo, Y. Quan, H. Zhao, Q. Yao, Y. Li, and W. Tu, “Tabgnn: Multiplex graph neural network for tabular data prediction,” arXiv.org, 20-Aug-2021. [Online]. Available: https://arxiv.org/abs/2108.09127. [Accessed: 13- Apr-2022].
[2]. X. Guo, Y. Quan, H. Zhao, Q. Yao, Y. Li, and W. Tu, “Tabgnn: Multiplex graph neural network for tabular data prediction,” arXiv.org, 20-Aug-2021. [Online]. Available: https://arxiv.org/abs/2108.09127. [Accessed: 13- Apr-2022].
[3]. Z. Li, Z. Cui, S. Wu, X. Zhang, and L. Wang, “Fi-GNN: Modeling Feature Interactions via Graph Neural Networks for CTR Prediction.” [Online]. Available: https://arxiv.org/pdf/1910.05552v1.pdf. [Accessed: 13-Apr-2022].
[4]. J. Lian, X. Zhou, F. Zhang, Z. Chen, X. Xie, and G. Sun, “XDeepFM: Combining explicit and implicit feature interactions for recommender systems,” arXiv.org, 14-Mar-2018. [Online]. Available: https://arxiv.org/abs/1803.05170v1. [Accessed: 13-Apr-2022].
[5]. P. Velickovic, G. Cucurul, A. Casanova, A. Romero, P. Li`o, and Y. Bengio, “Graph attention networks,” arXiv.org, 04-Feb-2018. [Online]. Available: https://arxiv.org/abs/1710.10903. [Accessed: 13-Apr-2022].
[6]. A. Kolan, D. Moukthika, K. S. S. Sreevani, and H. Jayasree, “Click-through rate prediction using decision tree,” Mar-2020.[Online]. Available: https://www.researchgate.net/publication/339992279_Click-Through_Rate_Prediction_Using_Decision_Tree. [Accessed: 14-Apr-2022].
[7]. “16.10. deep factorization machines— colab notebook ni SageMaker Studio Lab,” 16.10. Deep Factorization Machines -Dive into Deep Learning 0.17.5 documentation.
[8]. Sulistyowati, D. N., Yunita, N., Fauziah, S., & Pratiwi, R. L. (2020). “Implementation of Data Mining Algorithm For Predicting Popularity of Playstore Games In The Pandemic Period of COVID-19.” JITK (Jurnal Ilmu Pengetahuan dan Teknologi Komputer), 6(1), 95-100.
[9]. B. Trollinger, “Parking Lot Cities: Examining the Impacts of Parking Policy Reform on Autocentric Development Patterns in Buffalo, New York, and Hartford, Connecticut,” Ph.D. thesis, Tufts University, 2023.
[10]. A. Z. Hamadani, M. A. Ardakan, T. Rezvan, and M. M. Honarmandian, “Location-allocation problem for intra-transportation system in a big company by using meta-heuristic algorithm,” Socio-Economic Planning Sciences, vol.47, no. 4, pp. 309-317, 2013.
[11]. M. N. Al-Andoli, S. C. Tan, W. P. Cheah, and S. Y. Tan, “A review on community detection in large complex networks from conventional to deep learning methods: A call for the use of parallel meta-heuristic algorithms,” IEEE Access, vol. 9, pp. 96501-96527, 2021.
Cite this article
Wu,S.;Yang,T. (2024). Parking recommendation with meta-heuristic algorithms. Theoretical and Natural Science,34,281-290.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Computing Innovation and Applied Physics
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. X. Guo, Y. Quan, H. Zhao, Q. Yao, Y. Li, and W. Tu, “Tabgnn: Multiplex graph neural network for tabular data prediction,” arXiv.org, 20-Aug-2021. [Online]. Available: https://arxiv.org/abs/2108.09127. [Accessed: 13- Apr-2022].
[2]. X. Guo, Y. Quan, H. Zhao, Q. Yao, Y. Li, and W. Tu, “Tabgnn: Multiplex graph neural network for tabular data prediction,” arXiv.org, 20-Aug-2021. [Online]. Available: https://arxiv.org/abs/2108.09127. [Accessed: 13- Apr-2022].
[3]. Z. Li, Z. Cui, S. Wu, X. Zhang, and L. Wang, “Fi-GNN: Modeling Feature Interactions via Graph Neural Networks for CTR Prediction.” [Online]. Available: https://arxiv.org/pdf/1910.05552v1.pdf. [Accessed: 13-Apr-2022].
[4]. J. Lian, X. Zhou, F. Zhang, Z. Chen, X. Xie, and G. Sun, “XDeepFM: Combining explicit and implicit feature interactions for recommender systems,” arXiv.org, 14-Mar-2018. [Online]. Available: https://arxiv.org/abs/1803.05170v1. [Accessed: 13-Apr-2022].
[5]. P. Velickovic, G. Cucurul, A. Casanova, A. Romero, P. Li`o, and Y. Bengio, “Graph attention networks,” arXiv.org, 04-Feb-2018. [Online]. Available: https://arxiv.org/abs/1710.10903. [Accessed: 13-Apr-2022].
[6]. A. Kolan, D. Moukthika, K. S. S. Sreevani, and H. Jayasree, “Click-through rate prediction using decision tree,” Mar-2020.[Online]. Available: https://www.researchgate.net/publication/339992279_Click-Through_Rate_Prediction_Using_Decision_Tree. [Accessed: 14-Apr-2022].
[7]. “16.10. deep factorization machines— colab notebook ni SageMaker Studio Lab,” 16.10. Deep Factorization Machines -Dive into Deep Learning 0.17.5 documentation.
[8]. Sulistyowati, D. N., Yunita, N., Fauziah, S., & Pratiwi, R. L. (2020). “Implementation of Data Mining Algorithm For Predicting Popularity of Playstore Games In The Pandemic Period of COVID-19.” JITK (Jurnal Ilmu Pengetahuan dan Teknologi Komputer), 6(1), 95-100.
[9]. B. Trollinger, “Parking Lot Cities: Examining the Impacts of Parking Policy Reform on Autocentric Development Patterns in Buffalo, New York, and Hartford, Connecticut,” Ph.D. thesis, Tufts University, 2023.
[10]. A. Z. Hamadani, M. A. Ardakan, T. Rezvan, and M. M. Honarmandian, “Location-allocation problem for intra-transportation system in a big company by using meta-heuristic algorithm,” Socio-Economic Planning Sciences, vol.47, no. 4, pp. 309-317, 2013.
[11]. M. N. Al-Andoli, S. C. Tan, W. P. Cheah, and S. Y. Tan, “A review on community detection in large complex networks from conventional to deep learning methods: A call for the use of parallel meta-heuristic algorithms,” IEEE Access, vol. 9, pp. 96501-96527, 2021.









