1. Introduction

One of the most astonishing properties of quantum entanglement is its non-locality. It can be said that entanglement is the "breeding ground" for action at a distance [1, 2]. Essentially, remote action is instantaneous and discontinuous, making it impossible to describe through any spatial propagation process. Therefore, action at a distance cannot be approached by any continuous process with finite speed, lacking any characteristics of continuous motion. Moreover, entanglement does not involve the concept of speed; the interaction between entangled particles occurs simultaneously. This phenomenon was referred to by Einstein as "spooky action," with the lower limit of this action's speed being four orders of magnitude greater than the speed of light [3]. However, within the framework of relativity, any superluminal motion and action at a distance are deemed impossible, meaning energy and information cannot travel faster than the speed of light. To explain the simultaneity of wave function collapse, Bell's inequality and Bell's theorem have become crucial for understanding the existence of action at a distance or non-locality. So far, experimental results of Bell's theorem indicate that quantum non-locality or action at a distance truly exists.

Unlike the orthodox Copenhagen interpretation of quantum mechanics, holographic theory provides a new explanation for the principles of action at a distance. Within the framework of holographic theory, it can be assumed that the entangled quantum states are connected in a higher-dimensional space, which can be considered as AdS space. Holographic theory explains the EPR paradox through the AdS/CFT correspondence, where the entangled states in quantum field theory correspond to geometric structures in the higher-dimensional gravitational theory [4]. This means that the information of the entangled states is not local but realized through the geometric structure of the higher-dimensional space, thus explaining the nature of non-locality. Moreover, the holographic principle posits that all the information in a higher-dimensional space can be fully encoded on its lower-dimensional boundary [5, 6]. In this framework, quantum entanglement can be understood as the relationship between the entanglement entropy in the boundary CFT and the geometric background of the higher-dimensional gravity. This non-local transfer of information does not require superluminal propagation but is achieved through changes in the geometric structure.

Contemporarily, holographic theory has achieved several significant advancements in explaining quantum entanglement. Scientists have simulated holographic wormhole states on quantum computers to understand how quantum entanglement manifests in spacetime structures, providing new experimental validation for quantum gravity theories [7]. Additionally, researchers have demonstrated two new types of holographic entropy inequalities related to the topological properties of entanglement wedge nesting, further deepening the relationship between quantum entanglement and the holographic principle [8].

2. Methodology

2.1. Definition of Quantum Entanglement

Quantum entanglement is a quantum state where two or more particles are interconnected in such a manner that their properties cannot be described independently of each other. A unique aspect of entangled states is action at a distance: even if the particles are far apart, measuring one particle will still affect the state of the other particle. Quantum states have the property of superposition. According to the superposition principle, if a quantum state is in state | \( {ψ_{1}} \) > and state | \( {ψ_{2}} \) >, it can also be in any linear combination of these states:

|ψ>= \( {c_{1}} \) | \( {ψ_{1}} \gt +{c_{2}} \) | \( {ψ_{2}} \gt \) (1)

Here, \( {c_{1}} \) and \( {c_{2}} \) are complex numbers, known as superposition coefficients. Bell states are a set of special states where two qubits (quantum bits) are in a maximally entangled state, serving as an important tool for describing quantum entanglement phenomena. There are four Bell states, which are:

\( |{ɸ^{+}} \gt =\frac{(|00 \gt +|11 \gt )}{\sqrt[]{2}};|{ɸ^{-}} \gt =\frac{(|00 \gt -|11 \gt )}{\sqrt[]{2}}; \) \( |{ψ^{+}} \gt =\frac{(|01 \gt +|10 \gt )}{\sqrt[]{2}};|{ψ^{+}} \gt =\frac{(|01 \gt -|10 \gt )}{\sqrt[]{2}} \) (2)

Bell states involve two qubits in a completely entangled state, regardless of the distance between them. These states exemplify the typicality and complexity of quantum entanglement [9].

The strength of entanglement is typically quantified by entanglement entropy. Von Neumann entropy is a measure used to describe the information of mixed states, and the binary von Neumann entanglement entropy is given by the von Neumann entropy of one of the reduced states [10]. For pure states:

\( r{h_{OAB}}= |{P_{si}} \gt \lt {P_{si}}{|_{AB}}, S({ρ_{A}})= -Tr[{ρ_{A}} log{ρ_{A}}]= -Tr[{ρ_{B}} log{ρ_{B}}]=S({ρ_{B}}) \) (3)

Here, \( {ρ_{A}}=T{r_{B}}({ρ_{AB}}) \) and \( {ρ_{B}}=T{r_{A}}({ρ_{AB}}) \) describe the reduced density matrices for each partition. In holographic theory, entanglement entropy can be calculated through the geometric structure on the holographic surface.

2.2. EPR paradox and Bell's inequality

The concept of quantum entanglement was first proposed by Einstein, Podolsky, and Rosen in 1935, known as the EPR paradox, to question the completeness of quantum mechanics [3]. Specifically, examine a system composed of two spin-1/2 particles, A and B. After a certain time, A and B become completely separated and no longer interact with each other. When an observer measures a particular spin component of particle A, the spin value of particle B in the corresponding direction can be determined with certainty based on the conservation of angular momentum. Quantum entanglement demonstrates the non-locality in quantum mechanics, and Bell's inequality is an experimental tool to test this non-locality. Under the dual assumptions of locality and realism, this theorem establishes a strict limit on the possible correlation of results when two separated particles are simultaneously measured. Bell's inequality can be written as:

\( |{P_{xz}}-{P_{zy}}|≤ \) 1+ \( {P_{xy}} \) (4)

If Ax is positive: The spin state of quantum particle A observed on the x-axis is positive. P_xy corresponds to the correlation between Ax being positive and Bx being positive.

Additionally, de Broglie believed that the apparent randomness on the surface of quantum effects is entirely due to some unknown variables. If those extra variables are taken into account, the entire system is deterministic and predictable, adhering to strict causality. Such a theory is called the "hidden variables theory [11]. However, experiments have shown that Bell's inequality excludes local hidden variables as a credible explanation for quantum mechanics. As Bell himself stated, "No local hidden variable theory can reproduce all the statistical predictions of quantum mechanics” [2].

As shown in the Fig. 1, for the quantum correlation of spin (assuming 100% detection efficiency), the prediction of local hidden variable theory is represented by the solid line, while the prediction of quantum mechanics is shown by the dashed line. Assuming the angle \( θ \) between the two axes lies within the basic case angles mentioned above, the validity of the local hidden variable theory implies that quantum correlations should vary linearly. However, according to quantum mechanics, quantum correlations should vary as the cosine of the angle, cos \( θ \) .

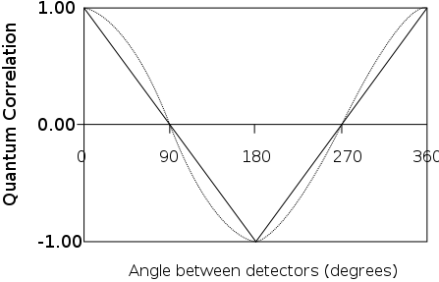
Figure 1. Quantum correlation as a function of the Angle between detectors (degrees) (Photo/Picture credit: Original).

2.3. Holographic theory

Holographic theory is an important theoretical framework in physics used to describe how a physical system in higher-dimensional space can encode its information on a lower-dimensional boundary [5, 6]. The basic concept of holographic theory is that all physical information of a physical system in n-dimensional space can be completely encoded in the (n-1)-dimensional boundary entropy. The core idea of holography is that the universe is an indivisible whole with tightly interconnected parts, where each part contains information about the whole. The implicit order must be extended to a higher-dimensional reality, which in principle is an indivisible whole that contains the entire universe with all its 'fields' and 'particles'. The process of encoding information in higher-dimensional space onto a lower-dimensional boundary is mainly realized through the AdS/CFT correspondence [4]. This means that under certain conditions, physical phenomena in higher-dimensional space can be described by physical theories on the lower-dimensional boundary, thereby greatly simplifying the analysis of complex systems. The metric of the d-dimensional AdS space is:

\( d{s^{2}}=\frac{{L^{2}}}{{z^{2}}}(d{z^{2}}+{η_{μʋ}}d{x^{μ}}d{x^{ʋ}}) \) (5)

Here, L is the radius of space AdS, z is the radial coordinate, \( {η_{μʋ}} \) is the Minkowski metric. On the boundary CFT:

\( {S_{CFT}}=\int {d^{d-1}}x{L_{CFT}} \) (6)

For a quantum state \( {ρ_{A}} \) , the entanglement entropy \( {S_{A}} \) is characterized as:

\( {S_{A}}=-Tr({ρ_{A}}log{ρ_{A}}) \) (7)

To calculate the entanglement entropy of a booundary, one can use the Ryu-Takayanagi Eq. (8):

\( {S_{A}}=\frac{Area({γ_{A}})}{4{G_{N}}} \) (8)

Here, \( {γ_{A}} \) is the minimal surface in AdS space for subregion A and \( {G_{N}} \) is the Newton constant. This method provides a geometric approach to understanding quantum entanglement phenomena.

Through holographic correspondence, the CFT states on the boundary of AdS space correspond one-to-one with the gravitational states inside the AdS volume. Each quantum state on the boundary maps to a state inside the AdS space [4]. This correspondence can be expressed as the formula:

\( {Z_{gravity}}[{ϕ_{0}}]={〈{e^{\int {d^{d}}x{ϕ_{0}}(x)Ο(x)}}〉_{CFT}} \) (9)

where the left side of the equation represents the partition function of the gravitational theory in AdS space, with \( {ϕ_{0}} \) as the boundary condition. The right side represents the expectation value in the boundary CFT, with \( Ο(x) \) as the operator in the CFT. This formula expresses how the gravitational theory in AdS maps to the boundary, offering a powerful tool for studying quantum gravity and quantum field theory.

3. Applications

3.1. Holographic Wormhole

The theory of wormholes can, to some extent, explain the non-local effects of quantum entanglement through the ER=EPR conjecture. This conjecture was initially proposed by physicists Juan Maldacena and Leonard Susskind, aiming to connect the spacetime structures in general relativity with the phenomenon of entanglement in quantum mechanics [12]. The core idea of the ER=EPR conjecture is that there exists a tiny, invisible wormhole between each pair of entangled particles. Although these wormholes cannot be traversed in the classical sense, they provide a natural explanatory mechanism at the quantum level, offering a theoretical foundation for the non-local effects observed in entangled particles. The concept of wormholes is based on the spacetime structures permitted by general relativity, which can connect two different points in spacetime. The initial theoretical framework for wormhole formation is the Einstein-Rosen bridge, which proposed a possible bridge between black holes and white holes [13]. The Einstein-Rosen bridge was initially introduced as a mathematical construct to explain the bipolarity of charges (positive and negative charges). It demonstrated a potential spacetime topology allowing two different points to be connected through a "shortcut." The ends of this bridge are located inside the event horizons of two black holes. This model is based on the Schwarzschild solution, a classical solution in general relativity used to describe non-rotating, uncharged black holes.

The Schwarzschild metric represents a static, spherically symmetric gravitational field, with its metric given by:

\( d{s^{2}}= -(1-\frac{2GM}{r}){c^{2}}d{t^{2}}+{(1-\frac{2GM}{r})^{-1}}d{r^{2}}+{r^{2}}(d{θ^{2}}+{sin^{2}}θd{ϕ^{2}}) \) (10)

Here, G is the gravitational constant, M is the mass of the black hole, c is the speed of light while (t, r, \( θ \) , \( ϕ \) ) are spherical coordinates. Einstein and Rosen extended the Schwarzschild metric to two symmetrical regions of the universe, thereby constructing a bridge. The mathematical formulation of this bridge involves introducing a new coordinate u such that:

\( {u^{2}}=r-2GM \) (11)

In this new coordinate system, the metric becomes:

\( d{s^{2}}= -(\frac{{u^{2}}}{{u^{2}}+2GM}){c^{2}}d{t^{2}}+4{({u^{2}}+2GM)^{2}}d{u^{2}}+({u^{2}}+2GM)(d{θ^{2}}+{sin^{2}}θd{ϕ^{2}}) \) (12)

This indicates that at u = 0, i.e., at r = 2GM, there exists a bridge connecting two different regions of the universe. The holographic principle suggests that certain non-gravitational quantum states can be represented alternatively as higher-dimensional gravitational states, a concept referred to as a holographic dual.

A team of researchers employed Google's Sycamore quantum processor, which consists of nine quantum bits, to simulate a simplified model of a traversable wormhole [14]. Seen from Fig. 2, the substantial quantum entanglement linking the two exterior regions of a black hole prevents travel between them. This limitation is 'holographically dual' to the prohibition against using entanglement to transmit messages faster than the speed of light. The top half of the image shows two particles, each representing a half quantum state, entangled with each other. The entanglement means the states of these two particles are correlated, irrespective of the distance separating them. The quantum entanglement of these particles has a holographic dual, which is depicted as an emergent wormhole in the lower half of the image. The left and right exterior regions are linked to the left and right quantum state respectively. These regions are parts of spacetime that are connected through the wormhole, illustrating the EP=EPR conjecture which points that each pair of entangled particles is connected by a tiny, non-traversable wormhole.

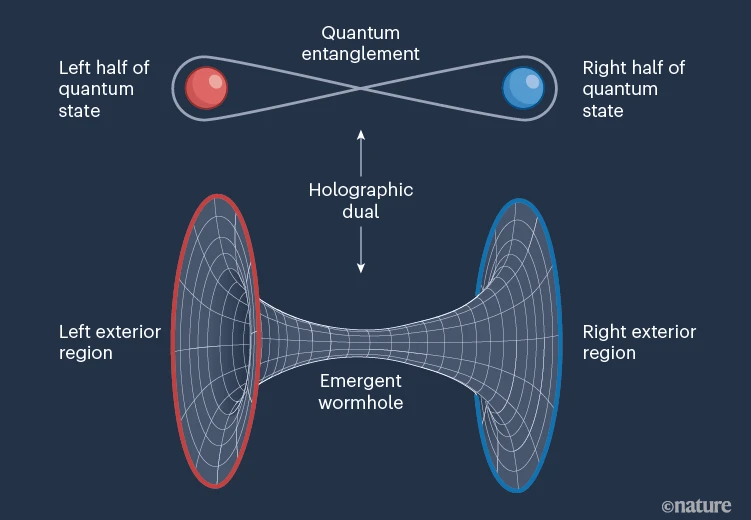
Figure 2. The concept of the EP=EPR conjecture, connecting quantum entanglement and wormholes (Einstein-Rosen bridges) [14].

3.2. Black hole information paradox

The black hole information paradox is one of the major challenges at the intersection of general relativity and quantum mechanics [15]. The paradox arises because black hole radiation (Hawking radiation) leads to the evaporation of black holes, resulting in the information loss, which conflicts with the principle of information conservation. In quantum mechanics, entropy is a measure of the amount of information that is inaccessible or the degree of uncertainty. For a black hole, this refers to the information content of Hawking radiation emitted during its evaporation. Stephan Hawking suggested that black holes emit radiation because of quantum effects occurring near the event horizon. This radiation essentially involves the creation of entangled pairs: one particle escapes the black hole while the other is absorbed into it. This implies that entanglement exists between the black hole and radiation. Scientists have made significant progress in understanding information preservation and the geometric description of quantum entanglement.

Black hole entropy is crucial for comprehending black hole thermodynamics and quantum gravity. According to the Bekenstein-Hawking entropy formula, the entropy of a black hole is proportional to the area A of its event horizon:

\( {S_{BH}}=\frac{A}{4{G_{N}}} \) (13)

This formula indicates that the black hole’s entropy is closely related to the geometric properties of its event horizon. Within the framework of the holographic principle, this relationship is further extended to reveal the deep connections between quantum field theory and gravity. The Ryu-Takayanagi Eq. (8) has a form analogous to the black hole entropy formula. Using the Ryu-Takayanagi formula, black hole entropy can be interpreted as the entanglement entropy in the boundary theory, thereby uncovering the holographic nature of black hole information.

By combining holographic theory and the Ryu-Takayanagi formula (9), one can study the changes in entanglement entropy during the formation and evaporation of black holes. During the evaporation of a black hole, the evolution of the minimal surface can be studied to track the flow of information, providing a geometric description of quantum gravity to address the information paradox. Furthermore, by discussing black hole information within the AdS/CFT framework, information can be considered as being encoded within the entangled structure of the boundary field theory, thus avoiding information loss. The latest research has introduced the island formula, which suggests that during black hole evaporation, certain regions (called islands) can contribute to entanglement entropy, thereby affecting the overall flow of information [16]:

\( S(R)=min\lbrace ext(\frac{Area(∂I)}{4{G_{N}}}+{S_{QFT}}(R⋃I))\rbrace \) (14)

Here, R is the radiation region; I is the island region; \( ∂I \) is the boundary of the island; \( {S_{QFT}}(R⋃I) \) is entropy of the quantum field theory region. The island formula provides a mechanism by which information can still be preserved through quantum entanglement during black hole evaporation, offering a powerful tool for resolving the information paradox. An extension of the Ryu-Takayanagi formula is the quantum extremal surface (QES) method. QES not only considers the area of the extremal surface but also includes the quantum correction terms for the entanglement entropy:

\( {S_{A}}=\frac{Area({γ_{A}})}{4{G_{N}}}+{S_{bulk}}({γ_{A}}) \) (15)

Here, \( {S_{bulk}}({γ_{A}}) \) is the bulk entropy contribution of the extremal surface \( {γ_{A}} \) . Through the QES method, it is possible to describe the structure and evolution of entropy inside a black hole more accurately. The Page curve is a theoretical construct that describes the entropy of a black hole’s radiation over time, particularly when the black hole evaporates through Hawking radiation [17]. It was introduced by Don Page and has significant implications for understanding the black hole information paradox. Fig. 3 is a simplified depiction of the Page curve.

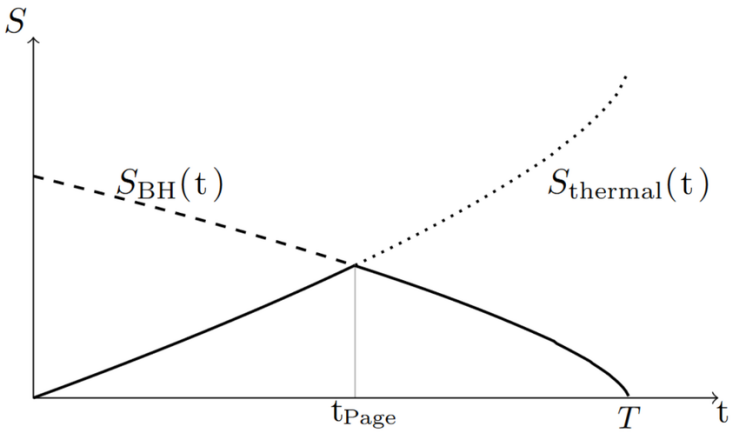
Figure 3. Illustration of the Page curve (Photo/Picture credit: Original).

As the black hole begins to emit Hawking radiation, the entropy of the radiation increases due to the creation of entangled particle pairs. At approximately half the lifetime of the black hole, the entropy reaches its maximum value. After Page time, the entropy decreases, indicating that the remaining black hole has less information content and the information starts being transferred to the radiation until the black hole completely evaporates. The entanglement entropy S of the Hawking radiation before Page time:

\( {S_{radiation}}≈\frac{t}{{t_{Page}}}{S_{BH}} \) (16)

After Page time:

\( {S_{radiation}}≈{S_{BH}}-\frac{t-{t_{Page}}}{{t_{Page}}}{S_{BH}} \) (17)

Replica wormholes suggest that information can be encoded in the correlation between radiation and the black hole interior. After the Page time, the wormhole configurations dominate, allowing for information to be extracted from the black hole’s interior via spacetime wormholes connecting real and simulated black holes. The replica trick entails computing the von Neumann entropy by analytically continuing the Renyi entropies to n=1. In this approach, gravitational path integrals encompass topologies that link different replicas through spacetime wormholes. This mechanism provides a geometric interpretation of quantum entanglement, where the entanglement entropy of Hawking radiation and the black hole is described by these connected topologies.

4. Limitations and Prospects

Although holographic theory has shown great potential in explaining quantum entanglement, there are still many detailed issues that need to be addressed. The problems that this theory needs to solve in the future can be mainly divided into theoretical, experimental, and application aspects. In the theoretical aspect, the mathematical calculations involved in the holographic principle require more complex and precise mathematical tools, such as CFT and AdS space. CFT is usually defined in high-dimensional spaces, and understanding and handling high-dimensional conformal symmetries and their associated algebraic structures is very complex. Moreover, the algebraic relationships of operators in CFT (such as OPE algebra) are very intricate, and analyzing these algebraic structures requires advanced mathematical tools, such as representation theory and harmonic analysis. The analysis of modal spaces in CFT in high-dimensional cases involves more complex integrals and special functions, and finding appropriate mathematical tools to solve these problems is challenging. On the other hand, AdS space itself is a spacetime with negative curvature, and its geometric properties are quite different from flat space. Analyzing and dealing with the impact of such curvature on physical phenomena requires complex differential geometric tools. In AdS/CFT duality, the boundary conditions of AdS space need to be handled carefully to ensure consistency with CFT. Therefore, boundary theory and geometric methods need to be improved to establish a more accurate holographic theory.

In the problem of the black hole information paradox, how information is transmitted and preserved between AdS and CFT involves many controversies and challenges. According to Don Page's calculations, information is not released uniformly during Hawking radiation but begins to be significantly released after a specific point in time (Page time). The holographic theory has not yet explained this timing and mechanism of information release. Some scholars have proposed the soft hair theory, suggesting that black holes may have "soft hair," i.e., perturbations on the event horizon that can record the information of matter falling into the black hole. This information can be released through Hawking radiation during the black hole's evaporation process. Another hypothesis is the firewall hypothesis, which posits the existence of a "firewall" at the black hole's horizon that destroys any matter approaching the black hole's horizon, ensuring no loss of information. However, this contradicts the smooth horizon hypothesis. Both hypotheses require further theoretical validation.

Experimentally, given the high dimensionality in the calculations of the holographic principle, it is challenging to design suitable experiments to test mathematical predictions. Additionally, holographic theory involves extremely high energy scales and very small spacetime scales, which place extremely high demands on the precision of experimental equipment. Current experimental technology is still difficult to balance with the theoretical level, and only certain aspects of holographic theory can be verified indirectly through experiments. Therefore, designing a direct experiment to verify the core of the holographic theory is a major challenge. The behavior of quantum entanglement in many-body systems is still not fully understood. Although scholars have proposed some possible simulation models, these speculations cannot provide practical significance for the explanation of quantum entanglement. Thus, how the holographic principle can be applied to the quantum entanglement of complex many-body systems is also an unresolved issue. Holographic theory also provides new perspectives for quantum computing, but applying the theory to practical quantum computing devices and algorithms requires further exploration. Of course, the application of holographic theory is not limited to physics; it can extend to information science, materials science, and other fields. Effectively applying holographic theory in interdisciplinary fields also needs further exploration.

There have been several significant advances in the field of holographic theory and quantum entanglement, with numerous research papers providing insights into current progress and directions. A recent study examines the entanglement entropy of dyonic black holes through the lens of doubly holographic theory. The researchers focused on the entanglement between the eternal black hole and Hawking radiation. They employed doubly holographic theories to analyze the radiation’s entanglement entropy, revealing a Page curve that aligns with the principle of unitarity. Additionally, using holographic entanglement density, they demonstrated for the first time that the saturated value of the entanglement entropy is twice the Bekenstein-Hawking entropy when considering a tensionless brane in double holography [18]. Another notable paper discusses the use of quantum gravity concepts to understand teleportation and traversable wormholes. This research emphasizes how holographic theories can simulate quantum teleportation by examining operator growth and its implications for signal transmission across different systems. They explore the potential for simulating holographic quantum gravity with quantum devices and present a specific approach—teleportation by size and the occurrence of size winding [19]. Research on holographic quantum simulations of entanglement renormalization circuits underscores the promise of leveraging holographic techniques to optimize tensor networks on quantum hardware. Utilizing circuits based on the multiscale entanglement renormalization ansatz (MERA), researchers successfully prepare the ground state of an L=32 critical, nonintegrable perturbed Ising model and measure long-range correlations on the ten-qubit Quantum trapped-ion computer. This method enhances the measurement and optimization of quantum systems, advancing the practical application of holographic principles in quantum computing [20].

5. Conclusion

To sum up, holographic theory significantly contributed to addressing quantum entanglement non-locality and the black hole information paradox. By employing the AdS/CFT correspondence, holographic principles reveal profound links between quantum entanglement and geometry. The theory uses the concept of tiny wormholes, or Einstein- Rosen bridges, to explain how entangled particles remain connected across vast distances, thus resolving the non-locality issue. In tackling the black hole information paradox, holographic theory introduces the island formula and replica wormholes. The island formula suggests that the interior of a black hole is part of the entangled system, implying that information is not lost but instead encoded in the radiation emitted. Replica wormholes provide a method to calculate the entanglement entropy of black hole radiation, supporting the idea that information can escape a black hole, thereby preserving quantum coherence. The advancements not only enhance the understanding of fundamental quantum mechanics and gravitational interactions but also offer promising pathways to unify quantum theory with general relativity, potentially leading to a more comprehensive theory of quantum gravity.