1 Introduction

Cryptography is an important guarantee for the information world nowadays [1]. For instance, in terms of network security, cryptography can be used to protect the security of network communications and prevent data from being stolen or tampered with by hackers; in the financial sector, cryptography can be used to encrypt card information, protect transaction data and prevent fraud; in government agencies, cryptography can be used to protect state secrets and personal privacy [2].

Number theory has been developed for thousands of years in the history of mathematics, possessing a complete system. As an essential branch of theoretical mathematics, number theory provides a safe and reliable encryption scheme for cryptography with complex operation processes. A few decades ago, with the help of modern computers, number theory started to be employed in modern cryptography, and efficiently enhanced information security on the internet [1]. Therefore, in modern societies, people need to realize the significance of number theory in the development of cryptography.

This literature review integrates some existing research and studies of Cryptography, and it will mainly focus on the introduction of the Rivest-Shamir-Adleman (RSA) and the Diffie-Hellman (DH) encryption methods and the number theory behind these two basic algorithms. The security analysis and the applications of these two algorithms will also be mentioned after the introduction of the algorithms. Finally, this literature review will discuss some effective solutions to some existing problems of RSA and DH algorithms. This literature review aims to instruct some basic knowledge of cryptography and to discuss the security risks of some algorithms.

2 Research status

Number theory as an important branch of mathematics mainly focuses on researching the properties and relationships of integral numbers. In cryptography, number theory topics, such as prime number, modular operation, Euler’s theorem, and Fermat’s little theorem, provide many essential tools to encrypt data [3]. The basic concepts and theories in number theory lay the foundation for encryption algorithms.

2.1 RSA

RSA algorithm represents Ron Rivest, Adi Shamir, and Leonard Adleman, who invented this algorithm in 1977 [4, 5]. RSA as an important milestone in modern cryptography is the first algorithm with the use of public keys, supporting both encryption and digital signature [5]. The security of the RSA algorithm is based on the difficulty of resolution of large integers, which is a topic that has been studied by mathematicians for hundreds of years [6].

2.1.1 Relevant number theory knowledge

• Euler Function [3]: \( φ(n) \) means the number of positive integers less than \( n \) that are prime to \( n \) . If \( n \) can be represented as a product of two distinct prime numbers \( p \) and \( q \) , then there is \( φ(n) = (p-1) (q-1) \) .

• Congruence (modular arithmetic) [3]: Given a positive integer \( m \) , if two integers \( a \) and \( b \) are satisfied that \( (a-b) \) is divisible by \( m \) , then it is called the congruence of \( a \) and \( b \) to the module \( m \) , denoted as \( a≡b (mod m) \) , where symbol “ \( ≡ \) ” represents the congruence. There are some properties of congruence numbers \( a \) and \( b \) , such as reflexivity, symmetry, transitivity, and so on.

• Modular Multiplicative Inverse [3]: If the modular inverse of an integer \( a \) is the integer \( x \) , \( ax≡1(mod m) \) , where \( m \) is the modulus, is satisfied.

• Euler's formula [3]: If \( a \) and \( n \) are prime to each other, then.

• \( a^{φ(n)}≡1(mod n) \) is satisfied. proof: refer to Lagrange's theorem.

• lcm: least common multiple.

• gcd: greatest common devisor.

2.1.2 Algorithm

• Generation of keys [3]

Chose two large distinct numbers \( p \) and \( q \) which are prime, and calculate their product \( n=p×q \) and the Euler’s function \( φ(n)=(p-1)(q-1) \) chose an integer \( e \) , such that \( 1 \lt e \lt φ(n) \) and \( gcd (e, φ(n))=1 \) , which means \( e \) is relative prime to \( φ(n) \) calculate \( d \) , a modular multiplicative inverse of \( e \) , which means \( e×d=1 (mod φ(n)) \) public key: \( (e, n) \) private key: \( (d, n) \) .

• Encryption [3]: Use integer \( m \) to represent the secret message M, such that \( m \lt n \) calculate the ciphertext \( c=m^{e} (mod n) \)

• Decryption [3]: calculate \( m=c^{d}(mod n) \) translate \( m \) back to message M

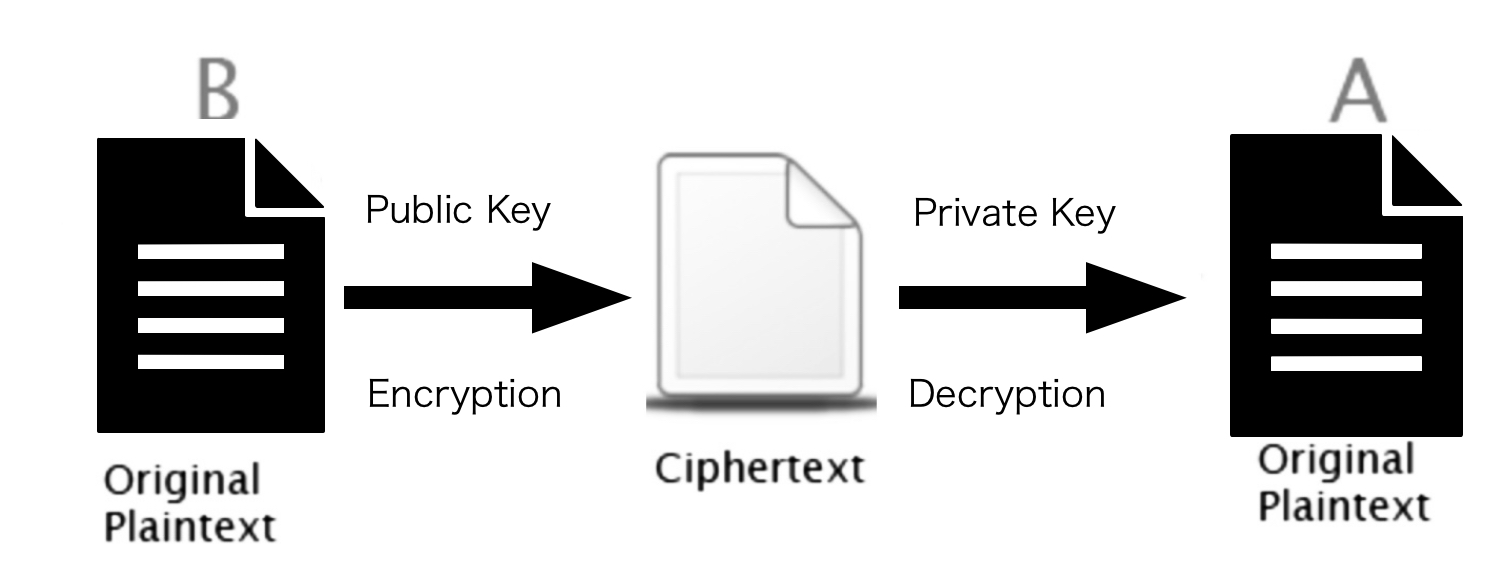
Figure 1. The schematic diagram of RSA (Photo credit: Original)

2.1.3 Security analysis

The security of the RSA algorithm mainly relies on the difficulty of the resolution of large integers [7]. At present, some variants of RSA are equivalent to the decomposition of large numbers. Whatever the attack method is, decomposing \( n \) is the most common one [3]. And it is now possible to factor large prime numbers of more than 140 decimal digits [3]. Also, Peter Shor an American professor of applied mathematics at MIT, showed in 1994 that factoring can be done in polynomial time on a quantum computer. Although people don’t yet have a quantum computer powerful enough to factor in large numbers, it might be a potential threat to the security of RSA in the future [7]. Anyway, to ensure the security of RSA, the modulus \( n \) should be selected to be larger, depending on the specific application [3, 5, 8]. Although people know there are lots of methods to attack and decode RSA, they usually don’t pose a real threat to RSA at least for now [3].

Here are two typical attack methods:

• Chosen-ciphertext attack (CCA)

One kind of cryptanalysis assault paradigm is the chosen-ciphertext attack (CCA), in which the cryptanalyst obtains information by decrypting specific ciphertexts. The information's secret decryption key might be attempted to be extracted by the attacker. RSA is vulnerable to a selected ciphertext attack.

• Coppersmith's attack

A class of cryptographic attacks against the RSA public-key cryptosystem is known as Coppersmith's attack, which is based on the Coppersmith approach. This technique is especially useful for attacking RSA when there is little public exponent e or when there is some knowledge of one of the secret key's prime factors [3]. When the public key e in RSA is adjusted to a lower number, encryption will be faster and easier to install, but it is not secure. Having bigger values for both e and d is the simplest strategy to fend off Coppersmith's onslaught [3].

2.1.4 Application of RSA

• Digital Signatures [2, 3]

An electronic signature is not a digital replica of a handwritten signature from a book; rather, it is the signing of an electronic document utilizing cryptography technology. Both identifying the signer and expressing their agreement with the content are its two key objectives [3]. A communication must be signed using a private key by the sender and validated by the recipient using the public key to produce a digital signature. RSA has additional advantages for this encryption method. This encryption technique can also benefit from RSA.

• Virtual Private Networks (VPN) [3]

VPNs also use RSA for key exchange and authentication when users connect to VPN servers, which helps to ensure secure data transit. While an asymmetric encryption algorithm, like RSA, is used to safely exchange symmetric keys between the VPN client and server, a symmetric encryption algorithm, like AES, is used for the actual data encryption. The speed and security of symmetric encryption are coupled with this hybrid encryption method.

2.2 Diffie-Hellman key exchange

The Diffie-Hellman (DH) key exchange, which securely exchanges keys via an unsecured channel, was first implemented in practice in 1976 and originally proposed by Whitfield Diffie and Martin Hellman. Its security relies on the difficulty of solving discrete logarithm problems [4].

2.2.1 Relevant number theory knowledge

• Modular arithmetic: Modular arithmetic is defined as finding the remainder of a number divided by another number. The basic formula of modular arithmetic is \( A mod B = A – (A div B) * B \) , \( div \) means divide and round off

• Discrete Logarithm Problem: The discrete logarithm problem is to an exponent \( x \) such that \( g^{x}≡y mod  p \) , given a prime \( p \) , a base \( g \) , and a result \( y \) .

2.2.2 Algorithm (shown in Figure 2 [9])

• Key generation [9]

Choose public numbers; \( p \) (usually at least hundreds of digits) prime number; \( a \) (usually 2 or 5) prime number, \( a \lt p \) .

User A Key Generation; Select private random number \( X_{a} (X_{a} \lt p) \) as a private key; Calculate public key \( Y_{a} \) \( (Y_{a}≡a^{X_{a}} mod p) \) .

User B Key Generation; Select private random number \( X_{b} (X_{b} \lt p) \) as a private key; Calculate public key \( Y_{b} \) \( (Y_{b}≡a^{X_{b}} mod p) \) .

• Encryption [9]

Exchange \( Y_{a} \) and \( Y_{b} \) through open channels. Calculation of ciphertext by User A: Secret ciphertext \( C \) , \( C≡Y_{b}^{X_{a}} \) mod p; Calculation of ciphertext by User B: Secret ciphertext \( C \) , \( C≡Y_{a}^{X_{b}} \) mod p.

Here is the proof of Encryption part: \( C≡Y_{b}^{X_{a}}≡(a^{X_{b}} mod p)^{X_{a}}≡a^{(Xa×Xb)}≡(a^{X_{a}} mod p)^{X_{b}}≡Y_{a}^{X_{b}}≡C (mod P) \) .

There are a total of 7 numbers \( a, p,X_{a}, Y_{a}, X_{b}, Y_{b}, C \) among which:

* Public numbers: \( a, p, Y_{a}, Y_{b} \) ,

* Private numbers: \( X_{a}, X_{b}, C \) .

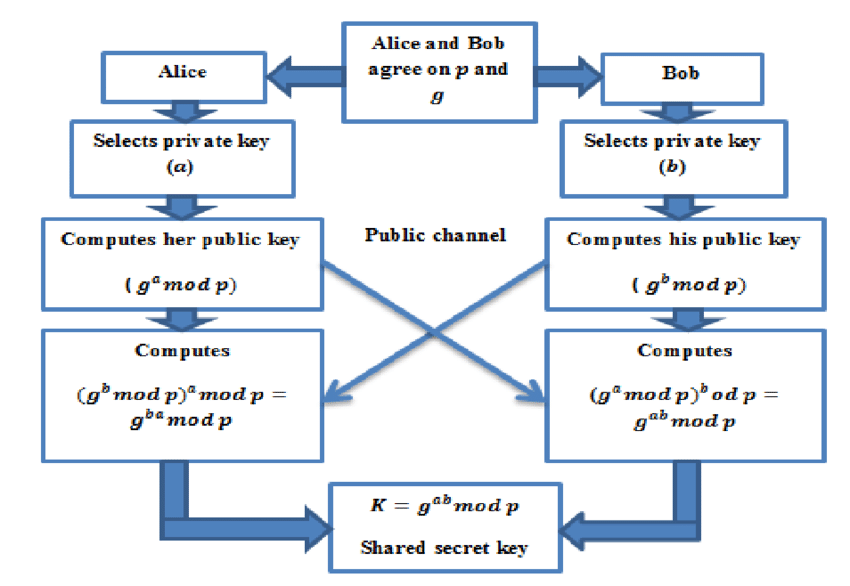
Figure 2. The encryption process of Diffie-Hellman [9]

2.2.3 Security analysis

In most cases, Diffie-Hellman allows people to securely exchange keys over an insecure channel, because of the difficulty of computation based on discrete logarithm problems. However, there are still many methods to attack a Diffie-Hellman Key exchange. The most general threat of Diffie-Hellman Key exchange is the man-in-the-middle attack (MITM), or on-path attack. An example of an MITM (Man-in-the-Middle) attack is active eavesdropping. This kind of attack features the attacker creating individual connections with each victim and sending messages between them, making each victim believe they are speaking with each other directly over a private connection [10, 11]. However, the entire conversation is under the attacker’s control. To accomplish this, the attacker needs to be able to spy on all pertinent communications between the two targets and insert new ones [10]. In many cases, this can be rather simple. For example, an attacker within the range of a Wi-Fi access point that is hosting an unencrypted network could position themselves as a man in the middle. (Shown in Figure 3)

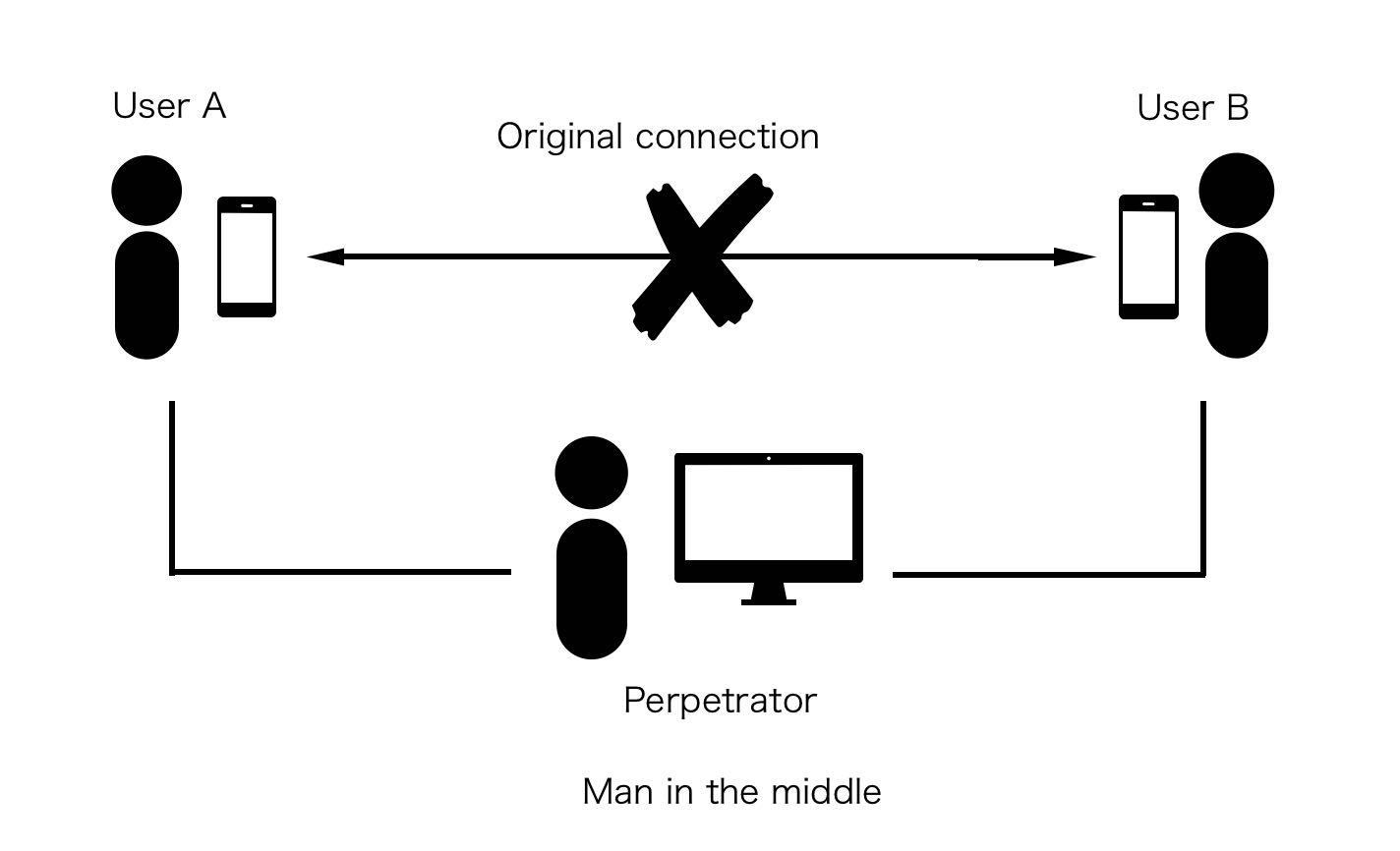
Figure 3. The schematic diagram of MITM (Photo credit: Original)

2.2.4 Application of Diffie-Hellman key exchange

• SSL

Netscape developed SSL, the industry-standard security technique, in 1994 to establish an encrypted connection between a web server and a browser [12]. This link ensures the confidentiality and integrity of all data transmitted between browsers and the web server. SSL is widely used on websites to protect their customers' online transactions. SSL uses certificates, private and public key exchange pairs, and Diffie-Hellman key agreements to provide privacy (key exchange), authentication, and integrity via Message Authentication Code [12].

• SSH

SSH is a widely used network security protocol for safe remote Internet login. SSH encrypts and verifies device connections using encryption technology. Because both FTP and Telnet transfer data in plaintext rather than encrypting it, the secure shell has taken the place of the less secure options on the network and system [12]. SSH, on the other hand, can compress, authenticate, and encrypt data automatically [12]. Diffie-Hellman is frequently used in SSH operations for key exchange and authentication.

• IPSec

The Internet Engineering Task Force (IETF) developed the IPSec (IP Security) suite of protocols as an addition to the Internet Protocol (IP) to facilitate the establishment of a communications channel between several machines [12]. Encrypting and authenticating IP packets is what it does, operating at the seven-layer model's IP layer. Like earlier protocols, IPSec establishes identities, preferred methods, and a shared secret through the use of asymmetric cryptography and Diffie-Hellman [12]. Before IPSec starts encrypting the data stream, some preparatory information exchange is needed. The Internet Key Exchange (IKE) protocol is used for this. Using the standard procedures, IKE creates a shared secret using Diffie-Hellman, after which they mutually authenticate. After that, encryption is performed using the secret key.

3 Discussion

Although the security of RSA and Diffie-Hellman are shown as reliable in most real-life applications, some experiments testing the endurance of RSA and Diffie-Hellman under different hack attacks point out that these encryption methods sometimes are vulnerable to these attacks. To maintain the safety of the Internet, it should upgrade the encryption methods or look for other novelty encryption methods. For instance, with the development of quantum computers, the security of RSA will be seriously threatened. Therefore, the future study, it can focus on exploring cryptographic algorithms that are resistant to quantum attacks, such as lattice-based encryption methods. Also, an experiment studying Diffie-Hellman showed that with the attack of Logjam, a flaw that allows MITM to present in “export-grade” Diffie-Hellman, any discrete logs in a specified 512-bit group could be computed in about a minute after a week-long precomputation [13]. Therefore, moving to stronger key exchange methods, for example, elliptic curve Diffie-Hellman (ECDH) key exchange, might be a priority for some areas in the Internet community [13].

4 Conclusion

Through the analysis of algorithms behind different methods in cryptography, the significance of Mathematical theoretical knowledge to the development of information technology is realized. For instance, the security of the RSA algorithm relies on the difficulty of the factorization of large integers; the difficulty of computation based on a discrete logarithm problem prevents Diffie-Hellman from being decoded easily, ensuring the security of the message exchange. Additionally, by comparing the efficiency, security, and application scenarios of different algorithms, it becomes more confident in choosing which algorithm is more suitable for a specific application scenario and how to improve the algorithm to operate better in the related field. Although existing literature has made great progress in the development of security and application of RSA and Diffie-Hellman, there are still many potential limitations and risks, such as the MITM attack. To avoid these attacks, it is necessary to find new feasible solutions to these threats and upgrade the algorithms. Finally, after the study of existing encryption methods, balancing the security and efficiency of the algorithm in practical applications is also a direction worthy of further discussion.